基于云理论改进AHP的灌区水土环境响应评价
徐存东 张锐 程慧 王燕 王荣荣 刘璐瑶
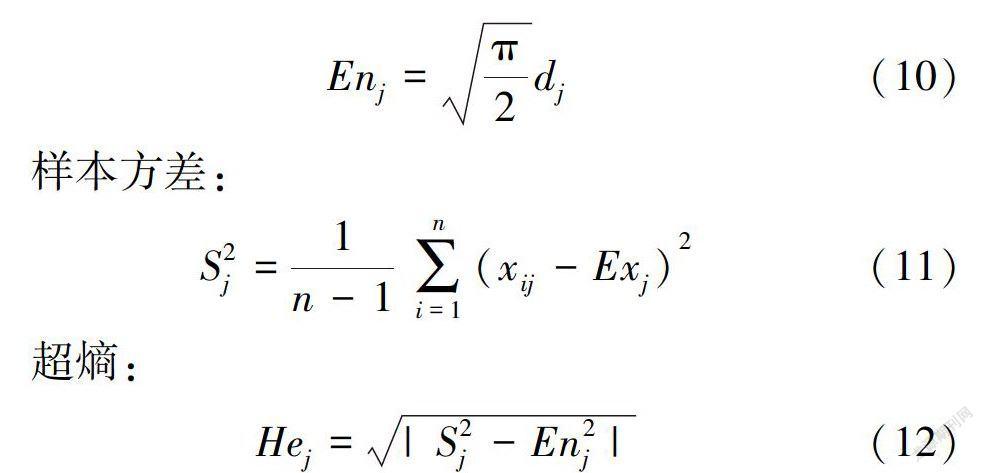
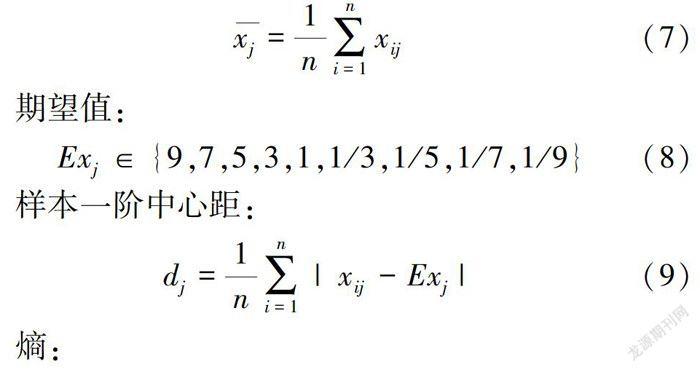
摘要:针对干旱灌区水土环境响应评价的不确定性问题,以甘肃景泰川电力提灌灌区为研究区,将不确定性云理论引入传统层次分析法中,通过对传统Satty标度进行改进,提出了基于云模型的标度准则,在此基础上,运用云标度准则构造两两判断矩阵,采用方根法对判断矩阵各行元素进行计算,进而得到了水土环境响应评价的云模型权重。结果表明:灌区水土环境的18个响应因子期望、熵、超熵分别为0.020~0.230、0.003~0.197、0.003~0.191,其中灌溉提水量和灌溉用水量响应最为强烈;状态层中,地表水和地下水响应相比于区域气候和土地利用更为强烈。利用云理论改进的层次分析法开展水土环境响应评价,通过不确定性云参数,定量揭示了评价过程中的不确定程度,将评价结果的中心值、随机性和模糊性有机结合起来,提高了评价结果的鲁棒性。
关键词:干旱灌区;水土环境;响应;云理论;Satty标度;不确定度;权重;景电灌区
中图分类号:X828;0211.3 文献标志码:A doi:10.3969/j.issn.1000-1379.2018.09.019
我国西北等地区土地资源丰富、光热条件充足,但水资源严重短缺,在这些区域发展提水灌溉是解决大片宜耕土地长期荒芜、确保区域农业和经济发展的基本措施[1]。然而,高扬程灌区的建设运行在取得显著经济效益的同时,伴随着土地沙漠化、土壤次生盐碱化、地下水水质恶化、地下水水位变化等水土环境问题[2]。当前针对水土环境方面的研究主要围绕着地表水、地下水时空变化及其成因,地表水与地下水相互转化,土壤盐渍化等方面。干旱灌区独特的地理位置及气候条件,加上高强度的人类活动,使得灌区的水土环境响应呈现出复杂模糊的特征,其表征也各不相同[3]。传统的水土环境响应评价主要从水资源开发和水土环境间的效应关系方面开展研究,如师彦武等[4]以水资源开发利用和水土环境间的效应关系为出发点,构建了干旱区水土环境与水资源开发间效应关系的评价指标体系;Kennedy等[5]对水文驱动因子与水土环境响应关系进行了研究。然而,干旱灌区水土环境响应评价是一个多层次驱动、多指标耦合的递阶分析问题,且其中某些指标的基本数据不能量化表征或无法准确获取[6]。因此,选择科学的评价体系和方法揭示这种响应程度的研究还需深入。
层次分析法是一种将定性概念转化成定量数值的多目标分析决策方法。由于该方法具有应用于多目标决策的独特优势,因此近年来广泛应用于各个领域[7-8]。然而,傳统层次分析法的Satty标度在专家评判时存在不确定性和模糊性[9]。目前,针对层次分析法的改进主要是对权重标度进行改进,这些改进的标度方法可较好地解决判断矩阵与专家判断思维一致性相脱节的问题,但仍以单个数值标度描述专家打分情况,打分过程中产生的不确定性和离散性易被忽略,同时将评价结果用一个精确数值来表征较为困难。云理论是李德毅在概率统计理论及传统模糊集理论的基础上提出的专门处理不确定性问题的数学理论,能较好地刻画事物的不确定性[10]。因此,笔者运用云理论对传统Satty标度法进行改进,探明干旱灌区水土环境响应的驱动要素,以期为干旱灌区水土环境改善与调控提供指导。
1 材料与方法
1.1 研究区概况
甘肃景泰川电力提灌灌区(简称“景电灌区”)是地处我国西北干旱区的大型提水灌区,光热资源充足,年均蒸发量为2433.8mm,年均降水量为185.6mm,蒸降比为13.11,干燥度为3.53,属典型少降水高蒸发区域[11]。景电灌区土地资源丰富,但水资源十分贫乏,因此建设大型提水泵站自黄河提水进行灌溉,最高提水扬程713m,年提水量约4.75亿m3。目前,灌区总面积586km2,高程为1596-1906m。景电灌区建成于20世纪70年代初,经过40多a的建设运行,地下水赋存区不断扩充迁移,地下水水位不断抬升,灌区封闭型水文单元多年地下水水位累计抬升5~8m,开敞型水文单元多年地下水水位累计抬升1.2~4.6m,地下水矿化度逐渐增高、水质不断恶化。灌区现有盐碱耕地0.67万hm2,盐碱化土地面积增加了近16%,且盐碱耕地中大部分土地为重度盐渍化和盐土。目前,土壤的次生盐碱化正改变着灌区的土地利用,天然植被不断衰败,2003-2014年植被衰退速率高达13.6%[12]。目前,人工提水灌溉产生的水土环境问题已成为景电灌区农业发展的制约因素。
1.2 云理论改进层次分析法
1.2.1 不确定性云理论
云模型是实现定性概念与定量数值转换的不确定性模型,概念的整体特性可用云模型的三个特征数值期望Ex、熵En和超熵He来表征,即C(Ex,En,He)[13]。期望反映云滴中心位置,代表数值分布的中心值;熵描述云滴模糊性和随机性,代表云滴分布的模糊性及离散程度(概率),反映期望的不确定程度;超熵是熵的熵,用于描述云滴凝聚度,代表熵的不确定程度,一般根据经验取值。考虑到正态分布是云模型中最具普适性及最为重要的一种分布,因此采用正态云模型[14]。
假设同一定量论域中有两个云模型CR1(Ex1,En1,He1)和CR2(Ex2,En2,He2),令CR1与CR2的代数运算结果为CR(Ex,En,He),对于CR=CR1/CR2,可采用下式[15]计算3个特征数值:
1.2.2 云模型标度准则
针对Satty标度构造判断矩阵时,不能摒除专家打分过程中产生的不确定性和离散性问题,以传统层次分析法1~9标度为基础,根据云模型理论,构建基于云模型的水土环境响应评价标度准则。
(1)标度云模型定义。根据Satty的标度值指标两两比较的重要性程度,定义9个云模型,见表1(Xi、Yj为相互比较的两指标)。
(2)云模型特征参数确定。①期望Ex。由Satty标度值,可用Ex4=9,Ex3=7、Ex2=5、Ex1=3、Ex5=1/3、Ex6=1/5、Ex7=1/7、Ex8=1/9、Ex0=1表示期望值。②熵En。由正态分布3En原则[16],可得云模型C1、C2、C3、C4对应的熵En1=0.33、En2=0.33、En3=0.33、En4=0.33;云模型C5、C6、C7、C8与云模型C1、C2、C3、C4互为倒数,可认为是标准云模型CR0(1,0,0)与C1、C2、C3、C4相除,可根据式(2)得到云模型C5、C6、C7、C8对应的熵En5=0.33/9、En6=0.33/25、En7=0.33/49、En8=0.33/81;Xi和Yj同等重要的云模型C0的熵En0=0。③超熵He。云模型C1、C2、C3、C4对应的超熵可根据经验取值[17],依次为He1=0.01、He2=0.01、He3=0.01、He4=0.01;与熵的求解类似,由式(3)可得云模型C5、C6、C7、C8对应的超熵He5=0.01/9、He6=0.01/25、He7=0.01/49、He8=0.01/81;Xi和Yj同等重要的云模型C0的超熵He0=0。综上,所构建云模型的标度准则见表2。
1.2.3 云模型权重
由构建的云模型标度对灌区水土环境响应指标重要性两两比较,进而建立判断矩阵(Rij)n×n,采用方根法计算响应指标的权重,对判断矩阵中各行元素进行计算,云模型权重Wi(Exi,Eni,Hei)计算公式[18]如下:式中:Exi为评价结果的中心值,代表评价结果的重要性程度;Eni为评价结果的不确定度值,代表数值分布的模糊性和离散性;Hei为Eni的不确定度值,代表数值分布的凝聚程度;i(i=1,2,…,n),j(j=1,2,…,n)为判断矩阵(Rij)n×n的行数、列数。
2 结果与分析
2.1 水土环境响应评价计算结果
2.1.1 评价指标体系构建
水土环境响应评价指标应全面反映灌区水土环境响应的实际情况,本文从景电灌区水土环境问题的实际出发,依据层次分析法的逐层递阶原理,以灌区水土环境为评价目标进行逐层分解,构建水土环境响应评价的目标一状态一响应多层次结构,见图1。
2.1.2 专家打分约束机制
2016年7月对灌区水土环境状况进行现场调研和数据采集的基础上,以构建的水土环境响应评价指标体系为基础,请相关学者、灌区技术人员及管理人员等专家分别对目标层、状态层、响应层进行两两重要性判断。专家打分主要基于期望值,期望最具代表性的数字特征,是定性概念转换后所有量化值的平均值,所构建打分约束机制计算过程如下。
同一层任意两两指标间n个专家对m个指标打分样本矩阵Xi=(xi1,xi2,…,xim),从而计算样本均值:
期望值:
Exj∈{9,7,5,3,1,1/3,1/5,1/7,1/9}(8)
样本一阶中心距:
熵:
样本方差:
超熵:
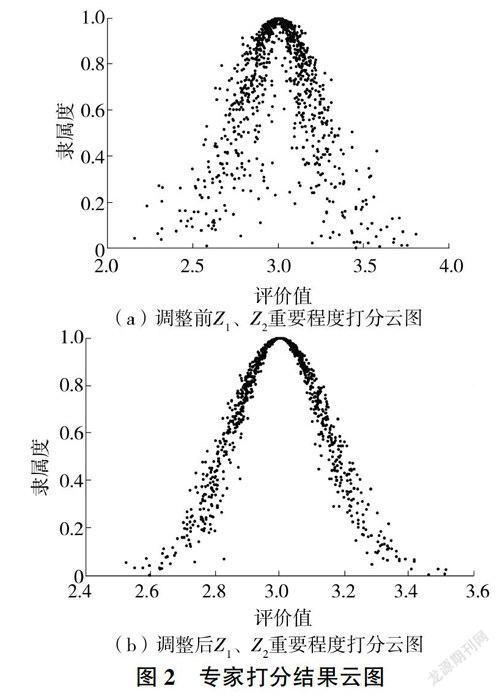
超熵是对熵不确定性的度量,超熵越大,距离期望的曲线越远,正态云呈现雾化状态,根据雾化性质与3En原则,当超熵HeEn/3,云图呈现出较为明显的雾化状态,因此将En/3作为正态云模型的雾化点。例如Z1与Z2重要程度初始打分云模型特征数值为(3.00,0.22,0.08),采用正向云发生器检验其有效性,对应云图见图2(a),可以看出云图分布比较分散,雾化严重,说明专家打分结果存在较大差异,导致评价结果不准确。将此信息反馈给专家,经过反复交流沟通,调整打分结果,直至云模型符合要求,调整后的评价云模型特征数值为(3.00,0.15,0.02),对应云图见图2(b),同理可对其他两两指标间打分的数字情况进行检验。
2.1.3 基于云模型权重的层次总排序
聘请灌区管理人员、技术人员及相关学者等10位专家进行打分,将专家对每一层指标间两两重要性程度打分结果用约束机制进行检验,通过反馈调整获得理想的期望打分值,进而构造基于云模型标度的判断矩阵,分别构造目标层、状态层以及响应层的判断矩阵。
由已建立的判断矩阵,运用式(4)一式(6)计算各判断矩阵各指标基于云模型权重的期望、熵、超熵,将各状态层各指标Y1、Y2、Y3、Y4与其对应的响应层指标的权重参数进行组合,进而得到各响应指标由期望、熵、超熵表示的合成权重Wi(Exi,Eni,Hei),将响应指标以期望Exi为第一排序要素、熵Eni为第二排序要素、超熵Hei为第三排序要素[19],进行层次总排序,进而得到水土环境响应评价响应层18个指标对目标层的层次总排序,见表3。
2.1.4 评价结果验证
依据上述评价指标体系,将德尔菲法与传统层次分析法用于水土环境评价中,3种算法下各指标权重相差不大,见表4(其中云理论改进权重仅用期望表示),验证了本文算法的正确性。
德尔菲法与传统层次分析法计算过程相对简单,计算复杂程度较低,但评价结果仅为单一数值,易因考虑信息的片面性而导致判断误差较大,虽然这两种算法在运算效率等方面具有一定优势,但所反映的信息有限。基于云理论改进层次分析法是用三个数字特征表示权重特征,期望代表权重,期望值的确定采用专家打分约束机制,将主观性问题的随机性和不确定性降到最低,所得权重结果更加合理可信,熵與超熵反映权重的不确定性,反映的信息更加丰富,由此可以看出,该算法为水土环境的响应评价提供了一种新思路。
2.2 分析与讨论
2.2.1 响应层评价
由表3可知,18个响应因子的云模型权重期望为0.020~0.230、熵为0.003~0.197、超熵为0.003~0.191,数值较小且分布较为集中,这18个响应指标都为“微敏感”因素,表明灌区水土环境针对单个因子的响应都不十分敏感,景电灌区的水土环境问题是多种因素长期作用的结果,只有经过长周期的量变积累才使灌区的水土环境产生宏观上的质变。
18个响应指标中对灌区水土环境演化响应相对较为剧烈的5个指标依次为灌区提水量Z1、灌溉用水量Z2、地下水赋存区Z9、地下水埋深Z6、地表径流系数Z3,这几个指标在提水灌溉后响应程度相比其他指标较为明显,尤其是灌溉提水量和灌溉用水量。同时,这5个因子都是和水有关的因子,表明水是驱动景电灌区水土环境响应的关键因素,是灌区水土环境响应最为敏感的要素。灌区普遍采用大水漫灌及集中洗盐等粗放的灌溉模式,导致地下水水位抬升、土壤盐渍化等一系列水土环境问题出现。
以灌区提水量Z1为例:其评价结果云参数权重为W1(0.230,0.197,0.191),期望为0.230,表明该评价结果的中心值为0.230,这个值是可能性最大的值,熵为0.197、超熵为0.191,数值较小且基本相同,表明评价结果分布较为集中,不确定度较小。该权重值不仅给出了评价结果的中心值,而且评价过程中的主观性得到了表征,相比于传统层次分析法,信息更丰富。
2.2.2 状态层评价
状态层四个指标地表水Y1、地下水Y2、土地利用Y3、区域气候Y4的云模型权重分别为WY1(0.408,0.481,0.481)、WY2(0.279,0.115,0.115)、WY3(0.127,0.343,0.343)、WY4(0.186,0.061,0.061),响应程度WY1>WY2>wY4>WY3。随着景电灌区提水灌溉的持续进行,地表水不断增加,水土环境有了明显响应。灌溉制度不合理和灌排系统不完善,灌区长期处于有灌无排状态,致使灌区地下水水位不断抬升,灌区的强烈蒸发使土壤表层不断积盐,进而造成土壤次生盐碱化。
3 结语
采用云理论改进的层次分析法开展干旱灌区水土环境响应评价,通过云模型的三个数字特征,将离散性、随机性及模糊性等不确定性特征有机结合起来,同时增加专家打分约束机制,使具有主观性的专家打分结果更为客观,更具可信性。相比于传统层次分析法,信息更丰富,不仅评价过程中的主观不确定程度得到了表征,而且提高了评价结果的鲁棒性。
18个响应因子权重期望为0.020~0.230、熵为0.003~0.197、超熵为0.003~0.191,状态层各指标的响应指标均为低敏感因子,其中响应最为强烈的指标为灌溉提水量和灌溉用水量。灌区水土环境响应的4个状态层因素中响应最为强烈的是地表水,其次为地下水,响应最为微弱的为土地利用,区域气候也起着一定作用。驱动灌区水土环境响应最关键的要素是水,气候及地质条件等也起着重要作用。
本研究只对传统层次分析法的1~9标度进行了改进,目前针对层次分析法的标度广泛使用的有指数标度、3标度等,而对这些标度尚未利用云理论进行改进以计算对比。同时,计算时采用的云模型分布为正态分布,如何选取不同情况下的不同分布的云模型还需要进一步研究。

