山洪沟道防冲建筑物壅水风险评估模型及应用
郭立兵 田福昌 曹鲁赣 苑希民
摘要:为合理评价山洪沟道防冲建筑物壅水风险,基于Saint-Venant方程组和Villemonte堰流公式,构建了防冲建筑物壅水风险评估水动力模型。根据防冲建筑物的实际情况和设计要求,将防冲建筑物概化为薄壁堰。将该模型应用于防冲建筑物分布密集的宁夏北武当沟,分析评估梯级防冲坎壅水风险,并提出优化措施建议。计算结果表明:所建模型能够较精确地模拟山洪演进过程和防冲建筑物壅水风险,充分体现了防冲建筑物的阻水效果。研究成果对沟道山洪的精细仿真模拟与风险评估具有一定参考价值。
关键词:山洪模拟;防冲建筑物;壅水风险评估;Villemonte堰流公式;北武当沟
中图分类号:TV131.2 文献标志码:A doi:10.3969/j.issn.1000-1379.2018.09.010
為了满足河道的抗冲刷要求,通常会在河道中修建防冲坎等防冲建筑物。防冲建筑物减小了河道过流断面面积,并增大局部水头损失,导致河道水流情况更加复杂。山洪暴发时,防冲建筑物前水位壅高,将对沿岸防洪产生诸多不利影响,合理评估山洪沟道溢流防冲建筑物壅水风险是十分必要的。
近年来,相关学者针对河道—维水动力模型的研究较多,成果颇丰。M.A.Nassar[1]利用一维SOBEK模型,模拟了灌溉改造工程对河道水位的影响;N.Pra-manik等[2]在缺少河道实测断面数据的情况下,利用卫星遥感影像建立了MIKE11模型,所建模型能够较精确地模拟印度Brahmani河流的洪水演进过程;Zhang X.等[3]提出了一种潮汐作用的表达式,并将潮汐作用表达式与Saint-Venant方程组结合,模拟了潮汐作用对洪水演进的影响;朱茂森[4]将河道—维模型应用于辽河流域的水质计算,模拟了水体污染物的迁移、扩散和衰减过程;郝红升等[5]构建了一维水动力模型,分析了电站排水及水库泄水对河流水环境的影响。虽然河道—维水动力模型已得到较多应用,但其在河道防冲建筑物壅水风险评估中的应用研究比较少见。
本研究基于Saint-Venant方程组和Villemonte堰流公式,以宁夏北武当沟为研究对象,建立山洪沟道防冲建筑物壅水风险评估的一维水动力模型,将防冲建筑物概化为薄壁堰,重点分析梯级防冲坎对沟道洪水演进过程的影响,评估防冲建筑物壅水风险,并提出减灾优化措施建议。
1 模型原理
1.1 沟道—维水动力模型
沟道—维水动力模型是基于Saint-Venant方程组建立的,并利用Abbott六点隐式格式[6-7]求解该方程组,Saint-Venant方程组[8]如下:式中;B为沟道过流横断面宽度;z为沟道水深;Q为沟道总流量;q为沟道单宽旁侧流量;t为时间;s为间距坐标;g为重力加速度;A为沟道过流横断面面积;i为沟底坡降;R为水力半径;C为谢才系数。
1.2 防冲建筑物概化与Villemonte堰流公式
针对防冲坎等防冲建筑物,在一维水动力模型中,可以利用局部水头损失的能量方程计算过流量[9],也可以利用一些相对简单的公式进行计算,比如Villemonte堰流公式[10]。Villemonte堰流公式适用于在淹没出流情况下薄壁堰的流量计算。在宁夏北武当沟研究区段内,沟道防冲坎采用铅丝笼水平护脚,防冲坎顶部厚度为0.4m,防冲坎顶部厚度和坎顶水头的关系通常满足薄壁堰条件;防冲坎位于河道底部,坎顶高程和下游水位的关系通常满足淹没出流条件[11-12]。根据沟道防冲坎的实际情况和设计参数,本研究将防冲建筑物概化为薄壁堰。Villemonte堰流公式为式中:Qs为防冲建筑物顶部过流量;a为流量系数;W为堰顶宽度;Hu与Hd分别为防冲建筑物上游和下游水位;Hw为堰顶高程。
2 应用实例
2.1 研究区概况
选择防冲建筑物分布密集、具有代表性的宁夏北武当沟为研究对象。北武当沟位于宁夏石嘴山市大武口区,由归德沟、韭菜沟汇合而形成。研究区段位于煤机铁路专用线3#桥和大武口拦洪库之间。研究区段内沟道总长7.2km,最大宽度457m,最小宽度100m,平均比降0.71%,堤防全部为土堤,临、背河坡比均为1:6。该区段防冲建筑物分布密集,共设置3座梯级防冲坎。北武当沟地处石嘴山市,该地区为宁夏两大暴雨中心之一,流域内水土流失严重,山洪暴发频繁(多出现在7-8月)。频发的山洪极有可能导致防冲建筑物处发生洪水漫溢,威胁两岸安全。针对该河段构建防冲建筑物壅水风险评估水动力模型,分析梯级防冲建筑物的壅水风险以及防冲建筑物对洪水演进的影响。研究区域位置见图1。
2.2 防冲建筑物壅水风险评估模型建立
2.2.1 河网概化与主要参数设置
北武当沟模拟范围为煤机铁路专用线3#桥至大武口拦洪库(中域),沟道全长7.2km。为了使模拟结果更加符合实际情况,利用沟道实测断面数据,在防冲建筑物前后及沟道蜿蜒曲折的区域,对沟道断面进行内插加密处理,加密之后壅水模型共设置124个沟道断面,其中沟道实测断面97个。沟道糙率是对沟道模型精度影响较大的参数,查阅相关地区资料[13],设定北武当沟沟道综合糙率为0.035。综合考虑模型稳定及运算效率等多种因素,设定北武当沟一维水动力模型计算步长为10s。
2.2.2 防冲建筑物概化处理
因北武当沟上段较陡,不能满足沟道抗冲刷要求,故结合城市功能区需要和沿线工程地质情况,在比降较大、存在安全隐患的重点沟段设置了3座防冲坎,分段调整比降。防冲建筑物顶部厚度较小,根据防冲建筑物的实际情况和设计参数,在壅水风险评估模型中,考虑防冲建筑物的阻水作用,将防冲坎概化为薄壁堰。
根据实测断面资料进行整编处理,模型内防冲建筑物参数设置见表1,1号防冲坎处沟道横断面见图2。
2.2.3 边界条件确定
模型上游控制边界条件为煤机铁路专用线3#桥断面设计洪水过程。北武当沟并无水文测站长期监测资料,考虑该区域暴雨洪水特性,根据区域暴雨洪水资料[14],利用设计暴雨推求北武当沟设计洪水,采用地区均衡法得到3#桥断面100a—遇设计洪水过程,见图3。
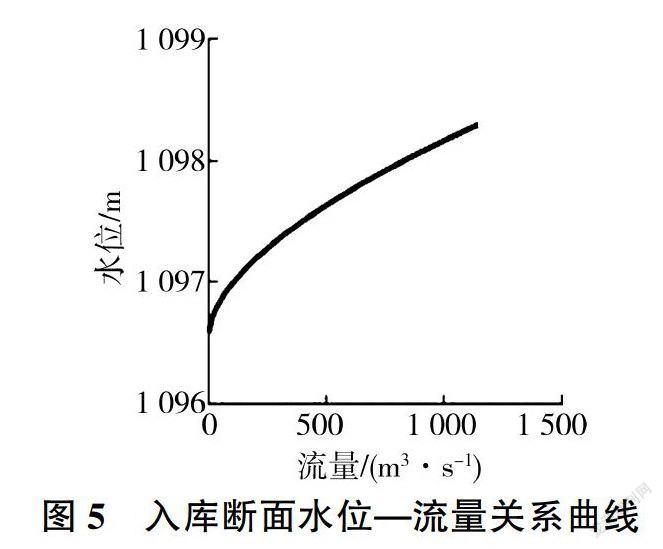
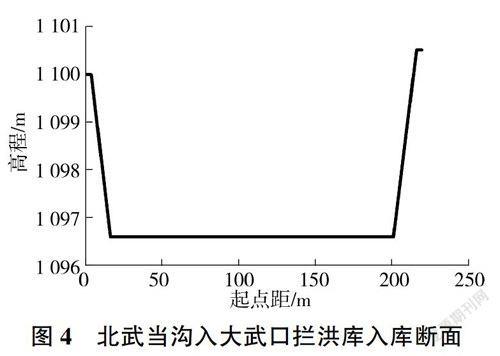
模型下游控制边界为大武口拦洪库入库断面(见图4),控制出流条件为该断面水位一流量关系。采用曼宁公式推求入库断面水位一流量关系,断面比降为0.0071、糙率为0.035,推求结果见图5。
2.3 山洪计算结果与风险评估建议
2.3.1 沟道洪水计算结果
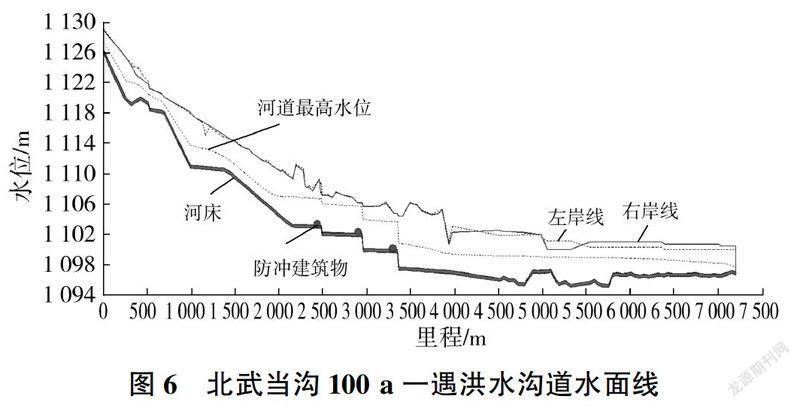
根据所建北武当沟沟道—维水动力模型,考虑梯级防冲坎壅水作用,模拟北武当沟100a—遇洪水演进过程,推算各断面水位、流量等,提取河道计算断面最高水位,连接各断面最高水位,绘制河道最高水面线,见图6。
由图6可知,在100a—遇洪水情况下,北武当沟洪水最高水位低于两岸堤顶高程,但3座防冲坎壅水作用尤為明显,最高壅水水位接近堤顶高程。如遇超百年稀遇洪水,则应特别注意洪水漫溢淹没影响,潜在风险较大。
2.3.2 防冲建筑物壅水风险分析
由北武当沟溢流防冲建筑物壅水风险评估模型计算结果可知,防冲建筑物很大程度上影响了沟道行洪,导致沟道水位壅高。经统计,北武当沟100a—遇洪水防冲建筑物壅水水位见表2。
当北武当沟遭遇100a—遇洪水时,1号防冲坎最高水位1106.75m,距左堤顶2.23m,距右堤顶2.56m,沟道最大水深3.95m,坎前最大壅水高度2.75m;2号防冲坎最高水位1105.70m,距左堤顶0.23m,距右堤顶0.20m,河道最大水深3.98m,坎前最大壅水高度2.78m;3号防冲坎最高水位1103.67m,距左堤顶0.95m,距右堤顶0.93m,沟道最大水深4.07m,坎前最大壅水高度2.87m。1、2、3号防冲坎顶部厚度分别是最大坎顶水头的0.15倍、0.14倍、0.14倍,顶部厚度小于0.67倍坎顶水头,防冲坎顶部厚度和坎顶水头的关系满足薄壁堰条件,验证了将防冲建筑物作为薄壁堰处理的合理性。分析可知,防冲建筑物壅水效果较为明显,壅水高度较大,导致沟道行洪能力减弱,将对两岸堤防安全和沿岸防洪等产生不利影响。虽然坎前最高水位未超过堤顶高程,但防冲建筑物处水位与堤顶接近,属防汛重点关注位置。
2.3.3 沟道防冲建筑物优化措施建议
由山洪计算结果和防冲建筑物壅水风险分析结果可知,防冲建筑物减小了沟道过流断面面积,壅水抬升作用较为明显,导致沟道行洪能力减弱。根据沟道防冲建筑物的水位、流量等,从降低防冲建筑物壅水风险角度提出以下几点优化措施建议:①在山区沟道满足抗冲刷要求的条件下,应尽可能避免或减少防冲坎等防冲建筑物,包括防冲建筑物的数量和规模;②为了减弱防冲坎的阻水效果和减小衔接处上下游水位差,防冲坎坎顶石料宜采用斜面石;③因防冲坎壅水水位接近堤顶高程,故为了避免堤防在长期高水位作用下发生流土、管涌和溃堤等险情,对防冲建筑物处的两岸堤防应进行加高、加固处理,并在迎水坡面设置混凝土防渗墙、防渗斜板及防渗趾墙;④为了避免超百年稀遇洪水造成洪水漫溢,可在防冲建筑物的某一侧或两侧修建适当的导洪堤,导洪堤结构可采用浆砌石重力式直墙。3结语
为了合理评估沟道防冲建筑物壅水风险,基于Saint-Venant方程组和Villemonte堰流公式,建立了适用于模拟防冲建筑物雍水过程的一维水动力模型。针对沟道防冲建筑物的过流特点,将防冲建筑物概化为薄壁堰。模型应用于防冲建筑物密集的宁夏北武当沟防冲坎壅水分析,结果表明:在100a—遇洪水情况下,防冲建筑物壅水效果明显,壅水高度较大,防冲建筑物处水位距堤顶较近,导致沟道行洪能力减弱,设置防冲建筑物的沟段属防汛重点关注位置。从降低防冲建筑物塞水风险角度提出了几点优化措施建议,所建模型适用于评估山洪沟道防冲建筑物的壅水风险,也可用于沟道山洪演进过程的精细仿真模拟。
参考文献:
[1]NASSARm A.One Dimensional Hydrodynamicmodel Simu-lating Water Stage in Open Channels(WS-1)[J].Interna-tional Journal ofmodeling Simulation&ScientificComputing,2010,1(2):303-316.
[2]PRAMANIK N,PANDA R K,SEN D.One DimensionalHydrodynamicmodeling of River Flow Using DEM ExtractedRiver Cross-Sections[J].Water Resourcesmanagement,2010,24(5):835-852.
[3]ZRANG X,BAO W,QU S,et al.One Dimensional Hydro-dynamicmodel Accounting for Tidal Effect[J].HydrologyResearch,2012,43(1-2):113-122.
[4]朱茂森.基于MIKE11的辽河流域一维水质模型[J].水资源保护,2013,29(3):6-9.
[5]郝红升,李克锋,庄春义.关于河道—维非恒定流水温预测模型的研究[J].四川大学学报(自然科学版),2005,42(6):1189-1193.
[6]ABBOTT M B.Computational Hydraulics:Elements of theTheory of Free Surface Flows[M].London:Pitman,1979:31-46.
[7]ABBOTT M B,IONESCU F.On the Numerical Computationof Nearly Horizontal Flows[J].Journal of Hydraulic Re-search,1967,5(2):97-117.
[8]苑希民,薛文宇,冯国娜,等.溃堤洪水分析的一、二维水动力耦合模型及应用[J].水利水电科技进展, 2016,36(4):53-58.
[9]衣秀勇.DHI MIKE FLOOD洪水模拟技术应用与研究[M].北京:中国水利水电出版社,2014:55-61.
[10]TULLIS B P,YOUNG J C,CHANDLERm A.Head-Dis-charge Relationships for Submerged Labyrinth Weirs[J].Journal of Hydraulic Engineering,2007,133(3):248-254.
[11]彭儒武,李保栋,王青,等.矩形薄壁堰贴壁堰流试验研究[J].山东农业大学学报(自然科学版),2002,33(2):197-202.
[12]高学平,张效先.水力学[M].北京:中国建筑工业出版社,2006:236-242.
[13]宁夏回族自治区水利厅.石嘴山市大峰沟治理工程初步设计报告[R].银川:宁夏水利厅,2014:43-65.
[14]宁夏回族自治区水文总站.宁夏回族自治区暴雨洪水图集[M].银川:宁夏回族自治区水文总站,1986:35-56.

