基于目标级联法的薄膜晶体管液晶显示器生产链协同规划
邵志芳,吴继兰
(上海财经大学 信息管理与工程学院,上海 200433)
0 引言
薄膜晶体管液晶显示器(Thin Film Transistor-Liquid Crystal Display, TFT-LCD)的生产过程分为列阵、组立、模组3个阶段,每一阶段有多个工厂进行生产。这种模式下的生产规划问题极其复杂,除了要考虑各个工厂内部几百道生产工序的问题,还要考虑工厂与工厂之间的各种上下游关系、供应关系、运输关系、库存问题等。Lin等[1-2]研究了生产链多厂规划方法,进行了多厂区的产能和生产混合规划[3],提出两步随机战略产能规划模型;陈可嘉等[4]提出一种混合整数规划模型,该模型考虑供应链物理约束、机器能力约束、工件加工顺序、订单交付期等约束,以成本最小化为目标,经分析验证,具有良好的排程效果;邵志芳等[5-6]分可外购和完全自产两种情境,分别研究了TFT-LCD产业生产排程及生产策略。然而,这些研究没有跳出一体化(All-at-Once,AAO)建模的思想,并假设生产链信息完全共享,剥夺了企业自主决策的权力,忽略了企业之间的信息博弈与交互过程。
目标级联法(Analysis Target Cascading, ATC)是解决非集中式、层次结构协调问题的一种新方法。ATC首先被应用于工业设计领域,例如Kim等[7]将ATC应用到飞行器等大型系统的设计。由于强大的协调能力与适应性,ATC开始被尝试应用到供应链管理领域,例如George等[8]的研究涉及供应链优化配置、供应链网络构建[9-12]等;Ling等[13]以成本最低为总目标,构造了一个供应链、工厂、运作车间的3层次ATC模型;黄英杰等[14]将蚁群算法与ATC结合,为车间调度问题找出了最优解;He等[15]考虑不同的合作方式,引入ATC和多目标线性规划平衡核心企业与其子企业的生产计划,达到成本最小或服务水平最优的目标;Li等[16]将系统分为路径规划层、单元规划层和作业规划层3个层级,利用ATC技术求解大规模Job-Shop调度优化问题;杨江波等[17]针对多车间分布式制造系统调度优化问题,结合车间实际生产情况,提出一种基于目标级联法和遗传算法的层次调度模型。总之,利用ATC协同技术进行生产规划的研究还很少,生产规划中的协同机制和协同算法还需进一步研究。
供应链建模的两种方法中,AAO是解决简单或复杂问题最直接的方法,该方法不追求系统的层次划分与组成,由单一的目标和所有约束共同构成模型;ATC是典型的层次化建模,其将复杂问题简单化,通过层次划分与协调机制求得可行解。与AAO相比,ATC的优势体现如下:①模块之间的共享信息少,减少了信息收集与传递的成本;②可解决分布式的复杂问题,能够用于大型系统的设计;③如果原问题无解,则在偏差容忍度下可以得到松弛解。
基于上述研究,本文考虑成本约束、库存约束、运输约束,引入时间维、产品维、工厂维,构建出更具复杂性并与现实贴近的ATC三层次模型解决TFT-LCD产业链的协同优化问题,同时构建该问题的AAO模型作为对比。
1 研究问题描述
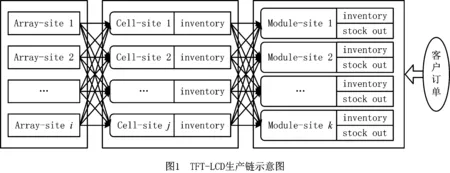
一个完整的TFT-LCD生产链由列阵(Array)、组立(Cell)、模组(Module)3段构成,如图1所示。假设Array阶段有i个工厂,Cell阶段有j个工厂,Module阶段有k个工厂,各个工厂掌握自己的相关信息,即工厂的产能、位置、厂与厂之间的运输费用、产品耗能等。Module是TFT-LCD生产的最后一个环节,也是与客户直接接触的环节,其在t时刻接到T时刻交付产品P的订单后,对上游企业进行生产排程及厂与厂的运输,以保证在T时刻按时交付订单,并使整个生产链上的费用最低。
假设如下:
(1)Array阶段没有库存(实际生产亦如此)。
(2)产品统一标识。经过3个阶段的加工,产品依然可以从本阶段追溯上阶段的形态与尺寸。因此,将3个阶段的产品都标示为m,并引进转化率表示产品在某一阶段加工引起的变化。
(3)Module阶段接受缺货惩罚。
2 数学模型构建
2.1 符号说明
(1)下标
m表示产品;
t表示计划期;
I,j,k分别表示Array,Cell,Module各阶段的工厂数量。
(2)参数
PCAmi表示Array阶段工厂i生产产品m的费用;
PCCmj表示Cell阶段工厂j生产产品m的费用;
PCMmk表示Module阶段工厂k生产产品m的费用;
PTAti表示Array阶段工厂i在t时刻的可用生产小时数;
PTCtj表示Cell阶段工厂j在t时刻的可用生产小时数;
PTMtk表示Module阶段工厂k在t时刻的可用生产小时数;
PTUAmi表示工厂i生产单位产品m所需要的小时数;
PTUCmj表示工厂j生产单位产品m所需要的小时数;
PTUMmk表示工厂k生产单位产品m所需要的小时数;
SCCmj表示单位产品m在工厂j每期的库存费用;
TTCij表示从工厂i运输到工厂j跨越的计划期;
TTMjk表示从工厂j运输到工厂k跨越的计划期;
TCCmij表示将产品m从工厂i运送到工厂j的单位运输费用;
TCMmjk表示将产品m从工厂j运送到工厂k的单位运输费用;
CVCmj表示单位产品m在Cell阶段的转化率;
CVMmK表示单位产品m在Module阶段的转化率;
SOmk表示产品m在工厂k的缺货损失。
(3)变量
PAmit表示t期工厂i生产产品m的数量;
PCmjt表示t期工厂j生产产品m的数量;
PMmkt表示t期工厂k生产产品m的数量;
SCmjt表示t期产品m在工厂j的库存量;
TQCmijt表示t期产品m从工厂i运送到工厂j的数量;
TQMmjkt表示t期产品m从工厂j运送到工厂k的数量;
Amkt表示t期产品m在工厂k的缺货量。
2.2 生产链协同规划的AAO模型
本文构建AAO模型作为ATC模型的对比模型,以此评价ATC模型所得解的精确性和有效性。在此,假定一个中央调控中心掌握供应链上各个阶段各个工厂的所有生产信息,并从供应链整体最优的角度进行建模,AAO模型如下:
(1)
(2)
(3)
∀k∈K,t∈T。
(4)
Where
(5)
SCmjt=SCj(t-1)+PCmjt-
(6)
(7)
(8)
PMmkt+amkt=Dmkt;
(9)
m∈M,k∈K,t∈T;
(10)
PAmit,PCmjt,PMmkt,TQCmijt,TQMmjkt,
Amkt,SCmit≥0。
(11)
2.3 生产链协同规划的ATC模型
利用ATC原理,将TFT-LCD生产链划分为3个层级。Psuper为模型的最顶层,负责整个生产链的协同优化,目标是3个阶段的总成本和反应变量的偏差最小;Psys为模型的中间层,表示上游生产链的协同优化,包括Array和Cell阶段,目标是这两个阶段的总成本和反应变量的偏差最小;Psub为模型的最底层,表示单个Array阶段的协同优化,目标是Array阶段的成本和反应变量的偏差最小。
进行ATC层级划分的本质是寻找层级之间的联系变量与反应变量。联系变量指上级传递给下级,并在下级模块之间共享的变量,同时下级经过分析模块的计算,向上级回传相应的联系变量;反应变量指上级传递给下级作为下级优化目标值的变量,同时下级经过分析模块的计算,也会向上级回传相应的反应变量。因此,联系变量与反应变量总是成对出现。


Psuper对整个生产链进行优化:
(12)
s.t.
(13)
∀k∈K,t∈T;
(14)
∀m∈M,k∈K,t∈T;
(15)
PMmkt+Amkt=Dmkt,
∀m∈M,k∈K,t∈T。
(16)
Where
(17)
其中:目标函数包括整个生产链的生产费用、库存费用和缺货惩罚费用;式(13)是ATC的协调机制的必要条件,也是Super层级(顶层层级)和System层级(中间层级)传递联系变量TQMmjkt与反应变量Cj的作用机理;式(14)表示产能限制;式(15)表示运入平衡;式(16)表示需求平衡。
Psys对上游生产链(Array阶段和Cell阶段)进行优化:
(18)
(19)
∀j∈J,t∈T;
(20)
∀m∈M,j∈J,k∈K,t∈[2,T];
(21)
∀m∈M,j∈J,t∈T。
(22)
where
(23)
其中:Psys以Super层级和System层级的联系变量与反应变量之间的差异最小为目标;式(19)是ATC的协调机制的必要条件,也是Super层级和System层级传递联系变量TQMmjkt与反应变量Cj的作用机理;式(20)表示产能限制;式(21)表示库存平衡;式(22)表示运入平衡。
Psub对Array阶段的工厂进行优化:
(24)
s.t.
(25)
∀m∈M,i∈I,j∈J,t∈T。
(26)
where
(27)
其中:Psub以System层级和Sub层级的联系变量与反应变量之间的差异最小为目标;式(25)为产能约束,即特定时刻t生产产品m所耗费的产能需小于总产能;式(26)为产量平衡约束,因为Cell阶段的产品均由Array阶段的产品加工而成,而且Array阶段处于卖方市场,产品生产出来即可全部卖出,所以任意的工厂i向j厂运输的产品数量总和为t时刻的产量总和。因为Array阶段设备昂贵,供小于求,所以不存在库存,也就不存在库存平衡表达式。
3 模型求解
3.1 模型参数
两个模型所用的参数完全相同。参数来自某TFT-LCD生产企业,该企业在Array,Cell,Module 3个阶段各有2个工厂。本文共涉及7(T=7)个计划期,由于运输延迟,最早要经过一个时间维度,上一阶段的产品才能运输到下一阶段作为原材料进行加工。假定Module工厂分别在3~7月份收到订单,为了满足这批订单需要确定Array工厂1~5月份的生产计划以及Cell工厂2~6月份的生产计划。
3个阶段的生产单位不同,分别为Lot,Sheet,Piece。其中:一个Lot可转化为10个Sheet,一个Sheet可以切割成约2个piece,且只考虑一种产品。此外,为了最大限度地刺激生产,设置了缺货惩罚成本SOmk=[500,500]。
其他关键参数如下:
Dmk: [0 0 300 600 1000 500 700;0 0 300 650 800 900 400 ];
PCAmi: [10,12] ;
PCCmj: [1.5,1.4]
PCMmk: [0.9,1];
PTAti: [350 300 300 300 300 300 300;350 300 300 300 300 300 300];
PTCtj: [300 300 200 400 600 400 900;400 300 600 600 400 300 600];
PTMtk: [500 600 1000 600 1000 500 700;500 500 500 700 1000 1000 500];
PTUAmi: [10,10];
PTUCmj: [1.2,1];
PTUMmk: [1,1];
SCCmj: [0.5,0.5];
TTCij: [1 1;1 2];
TTMjk: [1 1;1 1];
TCCmij: [0.2 0.2;0.2 0.1];
TCMmjk: [0.1 0.1;0.1 0.2 ];
CVCmj: [10 10];
CVMmK: [2 2]。
3.2 ATC模型协调机制设计
Kim在创立ATC方法时就证明过ATC的两个重要性质——非增(non-ascent)与收敛(convergence)。根据ATC原理设计协调机制如下:
2.RunPsuper,Psys
3.Do
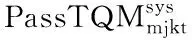
7.Until
8.converge(Psuper)&& converge(Psys) && converge(Psub)
9.If
11.WUM and go back to step 2
12.else
13.break
其中:converge要求所有变量收敛,即连续50次迭代后的结果之差小于给定的偏差(偏差设定为factor=0.001);consist要求Psys与Psub、Psuper与Psys层级所有对应的反应变量、联系变量之差小于最小容忍度才跳出循环(最小容忍度theta=0.000 1)。
4 结果分析
本文编程的实验环境为MATLAB 7.11.0(R2010b),直接利用内置函数fmincon求解非线性规划问题,经过52 041次循环迭代,耗费6小时25分41秒得到最终结果。
4.1 ATC模型中联系变量和反应变量的收敛与偏差




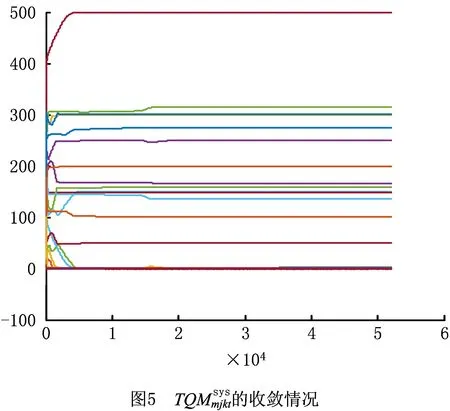


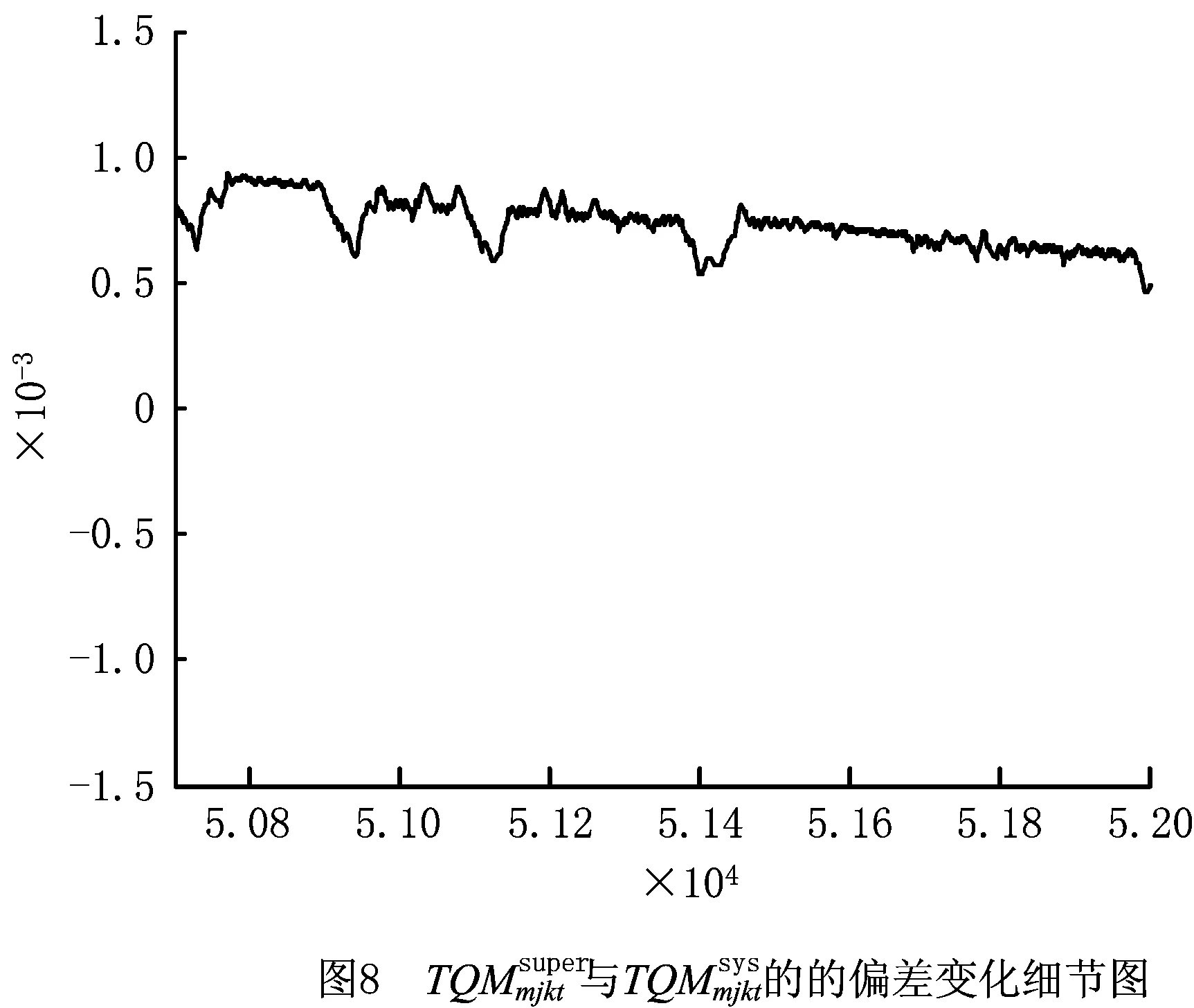
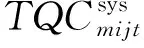
(2)反应变量的收敛与偏差
从图9和图10可以看出,从始至终,的取值大小及收敛速度基本一致,即初始值均为0,随后斜率趋于平缓;在约30 000次迭代后取值趋于稳定,随后在小范围内剧烈变化。



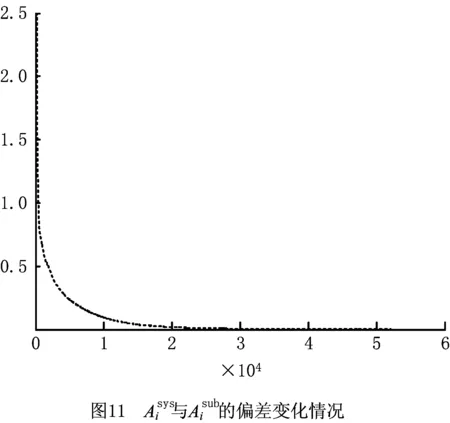

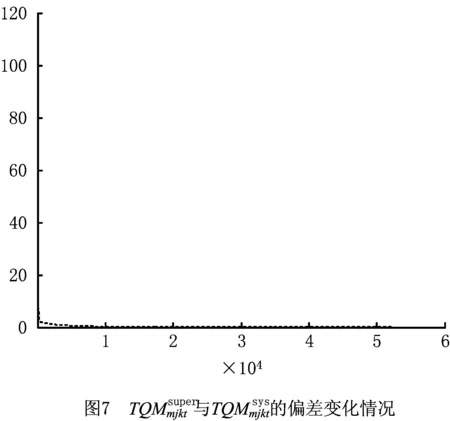
图13所示为偏差聚焦在结束50 000次左右的细节放大图。可见,偏差虽已趋于0,但仍然在小范围剧烈变化。


4.2 AAO模型与ATC模型结果对比
AAO模型和ATC模型成本结果对比如表1所示。总的来看,ATC得到的生产链最优解与AAO相同,正确率为100%;分解到各个层级上,Super层级产生的缺货费用、生产成本与AAO结果的正确率都保持在99.9%以上;System层级产生的运输费用、库存费用、生产费用与AA0结果的正确率都保持在99.9%以上;Sub层级产生的生产成本、运输成本与AAO结果的正确率都保持在99.9%以上。

然而,对比每一层级内的私有变量,得到的结果与AAO不尽相同。
(1) 完全相同的情况
ATC和AAO求解结果完全相同的变量如表2所示,可见二者关于PAmit,PMmkt,amkt的结果完全相同。

(2) 存在偏差的情况
如表3和表4所示,AAO和ATC关于SCmjt和TQCmijt的结果并不完全相同。此外,结果不相同的变量还有TQMmjkt和PCmjt。


结果出现差异的原因分析如下:
(1)方程有多个可行解
虽然AAO和ATC关于库存量SCmjt的结果不同,但是由成本对比可知,AAO和ATC的库存费用相同。库存费用=单位库存费用×库存数量(即∑∑∑SCCmj×SCmjt),其中SCCmj与时间t无关,只要库存总量相同,库存费用就相等。例如由表3的数据得32+18=25+25,0+75≈18+56,可见虽然具体的库存量SCmjt不同,但是仍然得到相同的库存成本。
由此可知,AAO和ATC模式下求得的SCmjt都是最优可行解。
(2)非严格的整数规划
ATC和AAO的求解利用的都是MATLAB中的fmincon函数,fmincon函数只能设定变量的上限和下限,无法规定变量为整数,本文的所有均通过四舍五入呈现,在四舍五入取整过程中,ATC和AAO的结果也会产生偏差。
4.3 对ATC方法的评价
(1)结果正确性
AAO是在参数变量完全已知的情况下,以费用最小为唯一目标得到的最优解。本文以AAO得到的结果作为参照量,评判ATC结果的正确性。从表1可知,ATC结果的正确率很高,表现为:①ATC通过循环迭代,最终得到的最小成本值与AAO相同;②细化到各个层级,相应层级的运输成本、生产成本、存储成本、缺货成本值也与AAO近似;③细化到单一变量,虽然部分ATC变量的取值与AAO存在偏差,但是经过验证,ATC的取值也是可行的最优解(不考虑四舍五入取整导致的偏差)。因此,从结果正确性的角度评价,ATC得到的结果真实可靠,可以用于生产链规划建模。
(2)时间复杂性
从时间复杂性的角度看,ATC的效率不高。AAO完成整个模型的运算只需要经过126次循环迭代,耗费7.5 s;而ATC完成整个模型的运算需要经过52 041次循环迭代,耗费6小时25分41秒。跳出循环要经过两次检验,即是否已收敛、联系变量和反应变量是否一致。本文收敛的判断条件是所有连续50次的偏差小于0.001,一致的判断条件是所有反应变量与联系变量的偏差均小于0.000 1。从图3~图13的收敛状态图可以看到,后期的收敛速度很慢,但是为了满足设定值,依然以很小的速度继续收敛。因此,整体的循环时间与偏差容忍度的大小设定有很大的关系。
(3)决策自主性
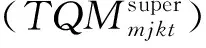
(4)信息私有性
ATC是一种多层级结构协调问题的方法,它允许层次结构中各元素自主决策,父代元素可以对子代元素的决策进行协调优化而获得问题的整体最优解。本文通过对变量的识别与对实际生产链的理解,将平面的链状结构转变为立体的层级结构。所划分的3个层级,每个层都有自己的私有变量,包括反应变量、联系变量和其他参数。例如,System层级包括向Super层级传递的TQMmjkt和Cj,向Sub层级传递的TQCmijt和Ai;私有的参数有TCMjk,PCCmj,SCCmj;私有的变量有PCmjt和SCmjt。在实际中,ATC和AAO的最大区别在于,ATC只需向上下级传递共享反应变量和联系变量,自己保有独立的私有变量。
由于信息传递与收集的成本较高,以及商业机密的保护性措施,生产链上各个企业能够互相分享的信息很少,AAO模型建立在假设所有信息都能共享的情况下,而ATC只需共享少量的联系变量和反应变量,从这一点来看,ATC方法更符合现实的情境。
5 结束语
本文利用层次化建模的思想对生产链的协同优化问题进行求解,设计了服从ATC的三层级模型。该模型将传统的链状结构进行重塑,构建了层次模型;模型涉及众多维度,包括产品维、工厂维、时间维,提高了对现实的仿真度;此外,模型包括缺货惩罚、运输平衡、库存平衡、产能限制等生产链建模的经典约束。
模型模拟了生产链上3个阶段(包括2间Array工厂,2间Cell工厂,2间Module工厂)在7个时间维度生产一种产品的生产排程,利用AAO得到的最优解作为评判ATC结果的参照解,得到如下结论:
(1)本文扩展了ATC在供应链规划领域的建模。模型变量主要考虑产品维、工厂维和时间维3个维度,模型约束主要涉及产能约束、库存平衡和运输平衡等经典约束,该模型很好地拟合了现实的TFT-LCD生产排程情况,并具有一定的复杂度。
(2)在建模方面,通过研究变量之间的交互性、关联性、共享性,设计了基于阶段成本的层级划分,将运输量作为联系变量,成本作为反应变量。本文将生产链链状结构重塑为ATC特有的层级结构的方法,对今后ATC在生产链建模领域的应用具有参考作用。
(3)验证了ATC用于生产链协同规划问题的正确性。相对于AAO的结果,ATC所求结果的正确率很高,在99.9%以上。
(4)相对于AAO模型,ATC具有良好的决策自主性与信息私有性,可以更好地模拟现实情境。
——基于行业数据的测度

