基于化学反应优化算法的车辆路径问题

蒋海青，赵燕伟，冷龙龙

(1.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014; 2.中国计量大学 现代科技学院，浙江 杭州 310014)

0 引言

半个多世纪的研究使车辆路径问题(Vehicle Routing Problem, VRP)从问题描述到求解方法都取得了丰硕的成果，但如何获得满意的求解方法依然是VRP中具有挑战性的研究领域[1]。VRP的求解方法大体分为精确式、启发式和智能优化3种，精确求解方法如动态规划、分支定界等[2]，启发式算法如节约法[3]、扫描法[4]及文献[5-6]对这两种算法的改进。由于启发式算法一般求到的是局部最优解，VRP目前的求解方法主要以智能优化算法为主，如遗传算法(Genetic Algorithm, GA)[7-8]、禁忌搜索(Tabu Search, TS)算法[9-10]、模拟退火(Simulated Annealing, SA)算法[11-13]、蚁群优化(Ant Colony Optimization, ACO)算法[14-17]。

石兆[18]总结智能优化算法在VRP的应用认为，禁忌TS算法搜索时间短，但禁忌规则难以确定;SA算法在不考虑计算时间时求得的解最好;ACO算法的搜索速度较慢，且较易出现早熟问题。鉴于智能优化算法的不足，近年来人们尝试从以下两方面进行算法改进：

(1)将多种算法进行集成 如Boon等[19]提出的集成差分算法，通过扩展TS算法求解车辆路径问题；Teymourian等[20]将改进智能水流算法(Enhanced Intelligent Water Drops, EIWD)和布谷鸟搜索(Cuckoo Search, CS)算法结合，并应用局部搜索混合算法(Local Search Hybrid Algorithm, LSHA)和后优化混合算法(Post-Optimization Hybrid Algorithm, POHA)局部搜索解决带有容量约束的车辆路径问题(Capacity Vehicle Routing Problem, CVRP)；Akpinar[21]将大规模邻域搜索(Large Neighbourhood Search, LNS)与蚁群算法ACO结合组成LNS-ACO算法求解CVRP问题，该算法应用ACO构造新的解，应用LNS进行解的改进，结合基于插入的局部优化方法在大量CVRP案例中获得了满意的结果；张景玲等[22]将量子进化算法与免疫算法结合，提出自适应免疫量子进化算法求取动态VRP；曹高立等[23]设计了混合量子算法求解CVRP，并采用二维量子位观测模型和可见度生成解改善求解效果。

(2)将新算法引入VRP的求解 例如Szeto等[24]应用人工蜂群(Artificial Bee Colony, ABC)算法求解CVRP,并结合insertion，swap多种局部优化方法改善解；Korayem等[25]提出运用灰狼算法求解CVRP；Tahayassene等[26]提出一种和声搜索算法meta-HSA(meta-harmony search algorithm)，通过设置求解器和优化器求解带时间窗的车辆路径问题(Vehicle Routing Problems with Time Windows, VRPTW)，并采用交换、2-opt的方法进行局部优化搜索,以提高解的性能；Yurtkuran等[27]提出类电磁场算法(Electromagnetic Field Algorithms, EFA)求解CVRP，并应用swap局部优化方法改善解的性能;Dorronsoro等[28]提出元胞遗传算法(Cellular Genetic Algorithm, CGA)求解CVRP，并构建基于交换和2-opt的局部优化方法提高解的性能。

上述改进算法虽然在解决VRP的有效性和优越性都得到了验证，但还是存在一些问题：①在子代解的构造中，当父代和母代解不合法时，就不能由其再产生子代解，从而限制了全局搜索范围；②两种算法集成时一般是由一种算法生成一个解，另外一种算法进行解的改善，较难实现两种算法的彻底融合。

化学反应优化(Chemical Reaction Optimization, CRO)算法是2010年由Lam等[29]提出的用于解决NP-hard问题的新型算法，算法根据分子在其势能面(Potential Energy Surface, PES)中能量越低状态越稳定的特性，通过模拟化学反应中分子间的相互作用来寻求分子最小势能。在求解时，通过其基本组成单元——分子结构来描述问题特性，即用分子表示问题的解，通过分子内部原子之间的反应(如碰撞、交换等)改变分子结构，寻求分子势能降低的途径。随着解的改进，分子势能逐步下降，当其势能最低时，分子达到稳定状态，这时的分子结构即为问题的最优解。与ACO,SA,GA等智能算法的不同之处是,CRO的参数意义简单且易于设置，只需要设置一个参数就能发生化学反应，每次反应都可以获得新的混合解，使其每代都有广泛的搜索空间。除此之外，其4种化学反应极易与其他智能算法结合，实现算法集成。因此，CRO已经被成功应用于连续性问题求解[30]，如电流优化问题[31]、网络编码优化[32]、自行车定位问题[33]、集合覆盖问题(Set CoveringProblem, SCP)[34]、背包问题[35]、任务调度[36]、频谱分配问题[37]等各类组合优化问题。尽管如此，文献[38]在对CRO的分析中认为其适合于目标问题的求解，而VRP与背包问题、分配问题及定位问题一样属于离散型NP-hard问题，且具有诸多相似性，因此本文探讨应用CRO算法解决CVRP，以期丰富CVRP的有效求解方法。为适应CVRP的特征，本文设计了包括配送中心、顾客整数序列的分子结构，采用节约法进行了分子的初始化，以提高初始解的质量；在分子的交换、撞墙反应中借鉴遗传算法的交叉、变异操作，应用分解反应扩大求解范围，将单个分子分解成保留父代、母代一定特征的两个分子，在合成反应中充分考虑了距离对成本的影响，将两点间的最短距离作为子代分子的选择依据；通过设置动态变化参数控制4种化学反应发生的频率，来提高算法的执行效率。为测试算法的有效性，本文对经典的benchmark基准实例的P，A问题进行了求解，并与当前先进算法进行了比较，实验结果显示，所提CRO算法具有一定的优势。

1 问题描述

CVRP可以描述为：由一个配送中心为多个顾客服务，车辆从配送中心出发，配送完成后返回出发的配送中心，问题的目标是获得总距离最小的最佳配送方案。将顾客与配送中心组成的网络图设为G=(N,A),其中：N=Nm∪Nc,Nm=0为配送中心集合，Nc=(1,2,…,c)为顾客点集合；A={(i,j):i,j∈N,i≠j}为点i,j的弧集合。K=(1,2,…,k)为车辆集合，dij为i，j的距离，车辆的载重限制为CQ,qi为i点需求。为便于建模，本文对问题进行如下假设：①车辆匀速行驶，路上无拥堵现象，路况平稳；②配送车辆数量不限，车辆类型只有1种；③客户需求已知并确定，每个客户必须且只能被服务一次。用模型表达如下：

(1)

s.t.

(2)

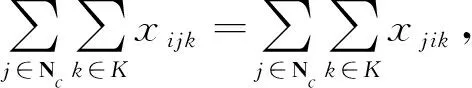
(3)

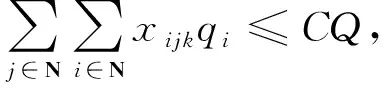
(4)

(5)

(6)

xijk∈{0,1},∀i,j∈N,k∈K。

(7)

其中：式(1)表示距离最短的目标函数；式(2)和式(3)保证每个顾客只能被服务一次；式(4)表示顾客需求限制；式(5)表示消除子回路；式(6)保证每辆车配送完后回配送中心；式(7)表示变量的取值。

2 化学反应优化算法

设分子ω的能量由势能PEω和动能KEω组成，在反应过程中，PEω逐渐减小， CVRP的目标是获得最短距离，因此本算法将PEω作为目标函数。但如果在算法设计时，单纯追求势能最小值，则极有可能只能求取到局部最优解。为了求得全局最优解，在CRO算法中通过调节动能，使新产生的分子ω′的PEω′即使大于PEω，ω′也能以一定的概率保留。CRO算法寻优的基本反应包括单分子反应和双分子反应，单分子反应主要有撞墙反应和分解反应，双分子反应主要有交换反应和合成反应。当分子之间的碰撞强度不大时，发生撞墙反应或交换反应，这两个反应一般获得原分子的邻域解，分解反应和合成反应在当分子发生剧烈碰撞时用于打破局域解。下面简单介绍这些反应：

(1)撞墙反应 指分子与容器壁发生碰撞后形成新分子的过程。若原分子为ω,则新分子ω′=neibour(ω)，即新分子为原分子的邻域函数，撞墙反应发生的条件为

PEω+KEω≥PEω′。

(8)

反应后，KEω′=(PEω+KEω-PEω′)×q，其中q∈[KELossRate,1]，KELossRate为能量损失最大百分比，损失的能量值保存在能量中心，用于提供分解反应所需能量，将能量中心的能量值表示为buffer。

(2)分解反应 指分子在容器中发生猛烈碰撞后，由1个分子分解为2个分子的过程。若原分子为ω，新分子为ω1和ω2，则分解反应发生的条件为

PEω+KEω≥PEω1+PEω2。

(9)

因在撞墙反应中，KEω逐渐减小，当式(9)不易满足时，若能满足

PEω+KEω+buffer≥PEω1+PEω2，

(10)

则能发生分解反应。

若式(9)成立，则KEω 1=temp×k，KEω 2=temp×(1-k)，其中temp=PEω+KEω-(PEω1+PEω2)，k为[0,1]的随机数；若式(10)成立，则KEω 1=(temp+buffer)×m1×m2，KEω2=(temp+buffer-KEω1)×m3×m4，其中m1，m2，m3，m4为[0,1]的随机数。

(3)交换反应 指容器中两个分子发生碰撞，各自被弹开后产生的变化。若原分子为ω1和ω2，新分子为ω′1和ω′2，则交换反应发生的条件为

KEω1+KEω2+PEω1+PEω2≥PEω′1+PEω′2。

(11)

反应后，temp=KEω1+KEω2+PEω1+PEω2-(PEω′1+PEω′2)，KEω′1=temp×k，KEω′2=temp×(1-k)，其中k为[0,1]的随机数。

(4)合成反应 指容器中两个分子发生剧烈碰撞后合成一个分子的过程。若原分子为ω1和ω2，新分子为ω′，则合成反应发生的条件为

KEω1+KEω2+PEω1+PEω2≥PEω′。

(12)

反应后，KEω′=KEω1+KEω2+PEω1+PEω2-PEω′。

3 CRO应用于CVRP问题

3.1 初始分子

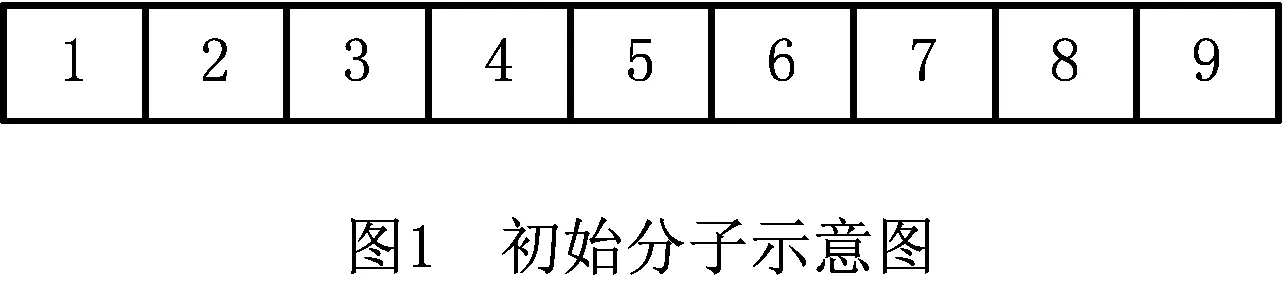
将分子结构表示为由配送中心和顾客组成的整数序列，对于有n个顾客的配送，将配送中心编号设置为1，顾客编号从2～n开始。首先对每个顾客i形成1-i-1的线路，按Sij=Ci1+Cj1-Cij计算插入顾客j后的Sij值,并将其由大到小排序，若最大Sij值对应的j顾客插入能满足载重条件，则将该j顾客插入1-i-1路线，直到所有顾客都能安排为止。如图1所示为构建的某初始分子，表示2辆车服务8个顾客，第1辆车服务2，3，7顾客，第2辆车服务1，4，5，6，8顾客，将此时的距离设置为初始势能值。

3.2 撞墙反应

借鉴GA的互换变异操作，撞墙反应采用位置交换法改变分子结构的流程如下：

(1)在容器库中随机选择一个分子ω。

(2)随机产生两个位置，交换两个位置的顾客，产生新分子ω′，其执行流程如图2所示。

3.3 分解反应

CRO算法分解形成的两条新路线不仅应保留原路线的部分特点，还要能扩大搜索范围。借鉴GA的循环交叉设计以下分解反应：从种群中随机选一个分子ω，再随机选一个位置pos，分解后的分子ω1保留pos前部分，将后部分反转，ω2保留pos后部分，将前部分反转，若原分子为34825679，pos=4,则分解后的两个分子分别为34829765和28435679，分解反应的执行流程如图3所示。

3.4 合成反应

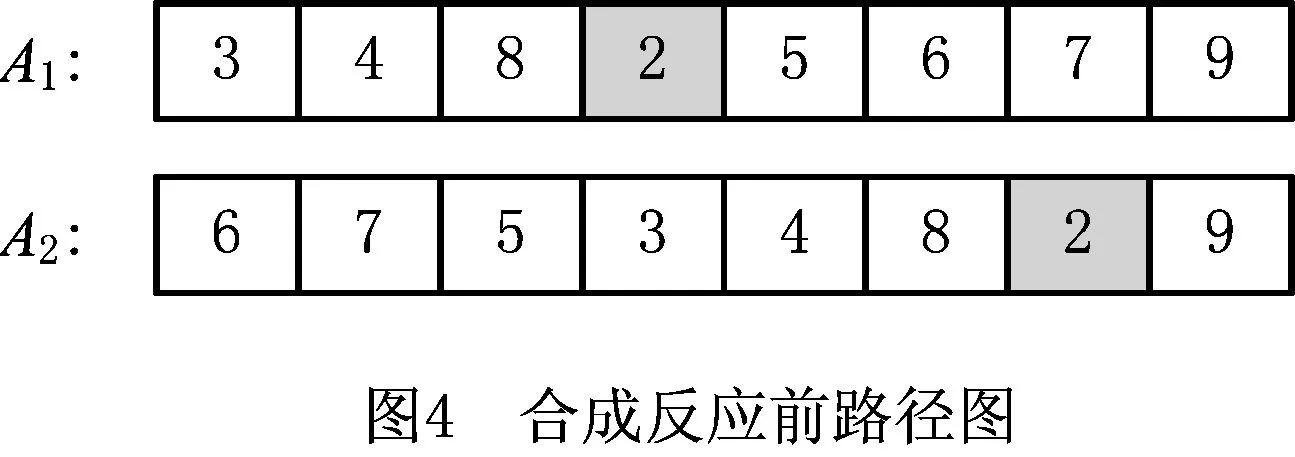
合成反应是将两条路线合并生成一条路线的过程。考虑到问题的目标是总路径最短，在合成过程中参考文献[39]，将相邻点距离最短的顾客点作为新路径节点。具体实施过程为：首先在种群中随机选择两个不相同的分子A1和A2；在分子A1中，随机选择一个顾客作为合成路径的第1个顾客点，分别计算A1，A2中该顾客点与其后相邻点的距离，选择最短距离所对应的顾客点为合成路径的下1个顾客，重复上述过程直到合成后的分子包含所有顾客。如图4所示，A1中pos=4，若A22～9点的距离大于A1中2～5点的距离，则将顾客5放入新分子的位置2。合成反应的具体流程如图5所示。

3.5 碰撞反应

参考文献[40]的交叉方法随机选择两个不同的分子A和B，随机选择分子A的顾客点ai和分子B的顾客点bj(i=j)，交换ai与bj后的顾客点，产生两个新分子，对新分子中重复的顾客点进行映射。当选择交换位置为4时，若交换前A，B分子分别为34825679和67534829，则交换后的分子A1和B1分别为34827569和67538249，碰撞反应的具体程序如图6所示。

3.6 算法流程

CRO求解CVRP问题的算法流程如图7所示。首先生成初始分子并计算其势能值，确定初始最小值，然后随机产生1个0～1均匀分布的t值，如果t大于预先设定的多分子反应概率MoleColl值，则执行双分子反应，否则执行单分子反应。对于单分子，将HitNumber与α进行比较，然后选择分解反应或撞墙反应；对于双分子，通过比较KE与β来选择相应的反应，具体执行过程如图8所示。

4 数据实验及分析

4.1 参数设置

CRO算法的主要参数有：初始分子的个数Popsize，影响单双分子反应选择的MoleColl,初始动能InitialKE，合成、交换两种双分子反应控制参数β1，分解、撞墙单分子反应控制参数α1，最大迭代次数num。当MoleColl<0.5时，双分子反应权重增大，反之单分子反应权重较大。图9所示为对P-n19-k2案例MoleColl取值的10次模拟平均结果，由图可知，该案例中MoleColl=0.3，0.8时取得了相同的目标函数，即单双分子反应权重对解的影响没有明显差异，因此本文取MoleColl=0.5。

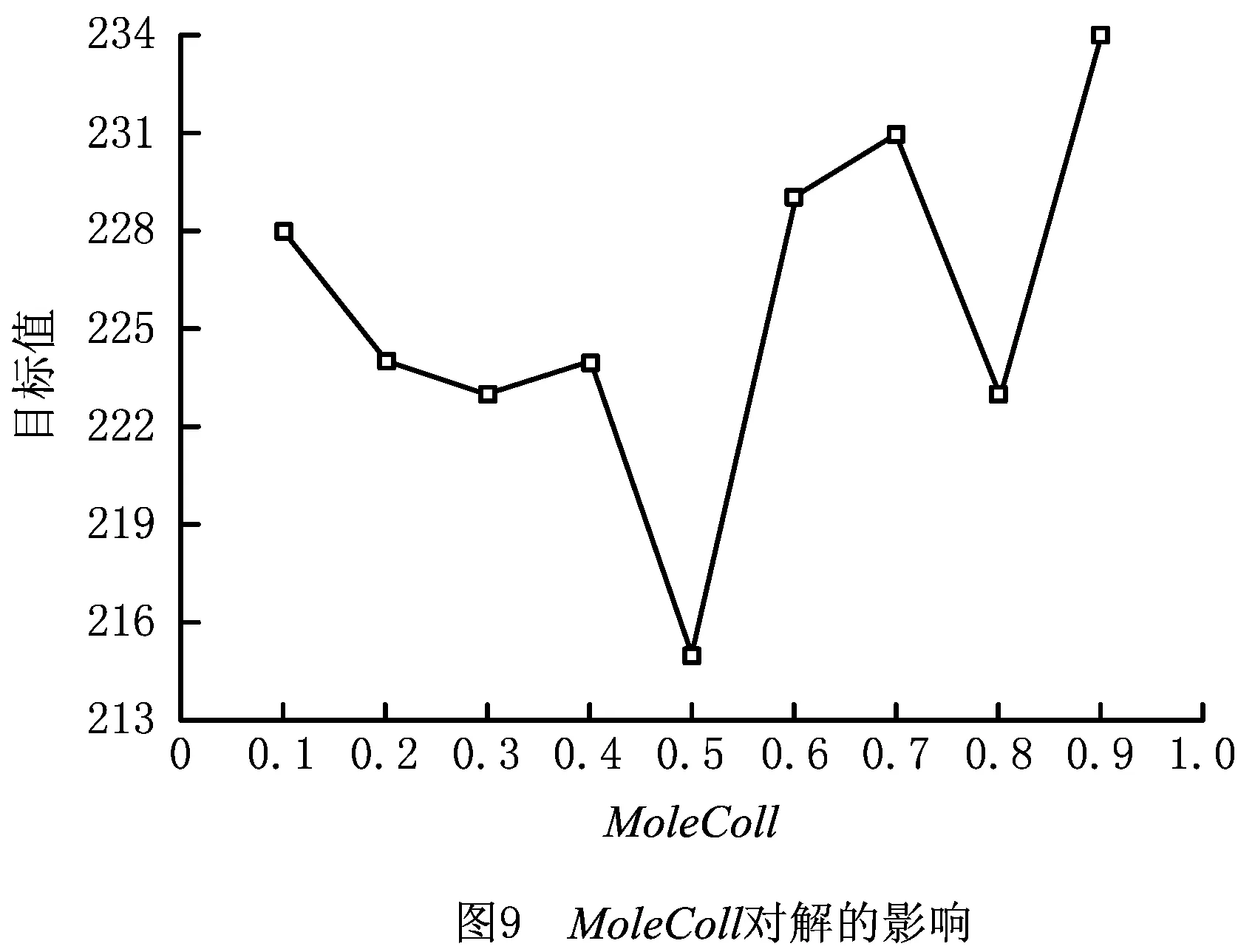
InitialKE是保证反应过程中能量守恒的参数，其设置过小易导致局域解[33];β控制合成、交换双分子反应的概率，其值越小，合成反应执行的几率越小，影响全局搜索，但如果过大，则碰撞反应的几率太小；α值影响分解、撞墙反应的发生概率，若α设置过大，则影响分解反应的发生概率，降低全局搜索，但过小又会影响碰撞反应的发生。本文按式(13)和式(14)设定α，β的值:

α=i/N×α1;

(13)

β=N/i×β1。

(14)

式中：N为总循环次数，i为当前循环次数，α1和β1为常数。

参考文献[33]的方法，设置初始参数α1=0，β1=0，InitialKE=179，Popsize=50，然后依次改变参数InitialKE，β1，Popsize，α1的取值。以P-n19-k2为测试案例，图10所示为参数取值与目标函数和CPU用时的关系。由图10a和图10b可知，α1，β1设置太大或太小均不能获得最佳解，说明几种反应的权重系数对求解结果的影响具有随机性，当α1=40，β1=80时解最小，其CPU用时的变化极小(不超过4 s)；由图10c确定InitialKE=716；由图10 c确定InitialKE=716;由图10d种群与解及CPU的关系确定Popsize=150。

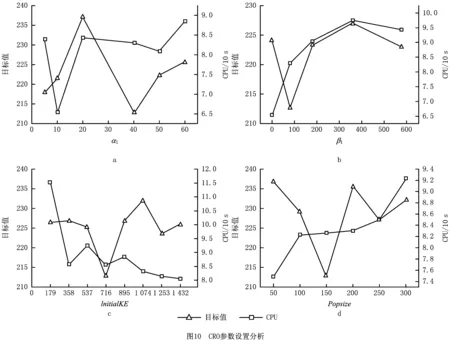
迭代次数越多，分子越能充分地在解空间进行搜索，分子间的信息交换越充分，越能搜索到更好的解。图11及表1所示为迭代次数与解的关系，表1第2列是P-n19-k2取上述参数随机运行10次的平均值，第3列是其平均CPU用时，图11所示为与表1对应的图。由图11可知，随着迭代次数的增大，解得到了改善，但当其增大到一定程度后(3 000代后)，对优化结果的提升效果趋小，但其CPU用时却大幅提高。因此，本文在优化结果和计算时间之间寻求一个平衡，将最大代数设为3 000。

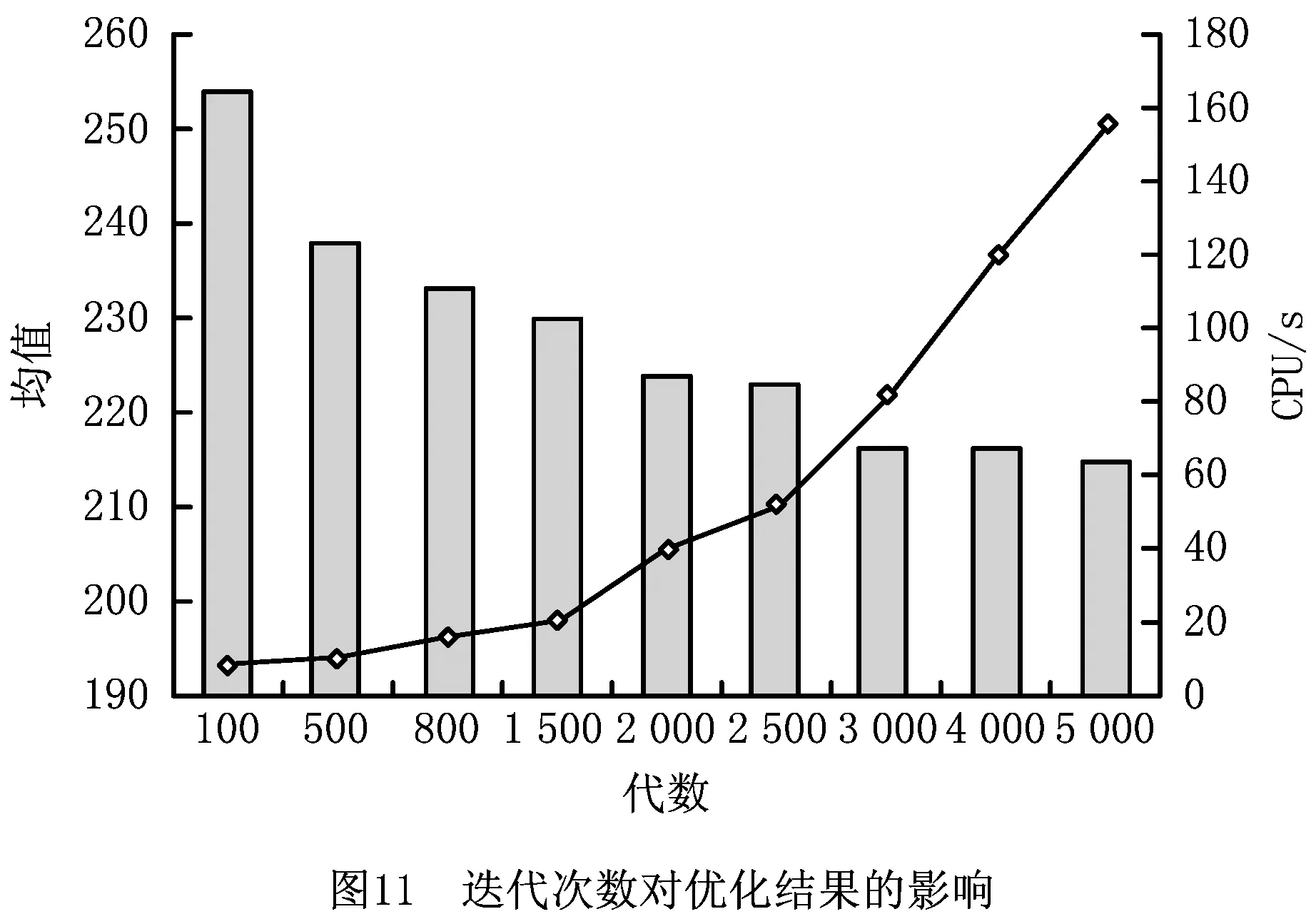
结合图10和图11的结果及后期大量的实验，本文参数设置如下：MoleColl=0.5，InitialKE=716，Popsize=150，α1=40，β1=80，num=3 000。

4.2 结果分析与比较

本次计算采用MATLAB 7.0编程,计算机的配置为Pentium(R)Dual-Core E5300 2.60 GHz CPU，8 GB RAM，每个案例计算10次，以最大循环次数为结束条件。为了测试算法的效果，将本文设计的CRO算法与标准库案例结果进行对比，标准库案例结果来自网址为http://www.bernabe.dorronsoro.es/vrp/的网站，数据采集的时间为2017年2月10日。表2所示为CRO算法的计算结果和标准库最优解的比较。其中：BKR为该标准库的最优解，Best为本算法求得的最佳解，Avg为平均值，第五列表示平均CPU用时，Dev为偏差。偏差的计算公式[25]如下：

由表2可知，在对标准库9个代表性的P，A案例求解中，CRO有4个案例取得了与标准库相同的最优解，占总案例(9个)45%，其他未获得最优解案例的偏差值绝大多数不超过5%。为了进一步验证CRO算法的求解效果，将其与文献[21]3种策略的大规模领域搜索(LNS)算法进行比较，比较结果如表3所示，表中：fbLNS，fwLNS分别表示不同策略LNS算法的最好解值和最差解值，fCRO表示本算法的最好解值；bRPD，wRPD表示本算法与LNS的最好解和最差解的相对差异百分比：

(16)

(17)

两种算法的CPU用时比较如表4所示。

表3 CRO与LNS结果比较

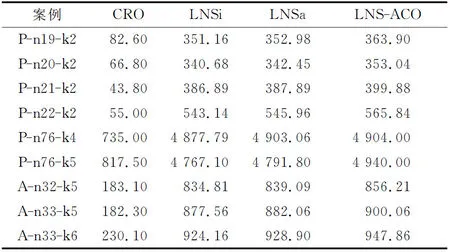
由表3可知，CRO算法在绝大多数案例中都取得了与LNS相同的最优解，部分结果优于LNSi，没有结果优于LNSa和LNS-ACO，但平均解偏差与LNSa和LNS-ACOCRO相比均不超过1%，与LNSi的平均结果相近，说明CRO算法具有较强的搜索能力。由表4可知，相比LNS算法，CRO算法的CPU用时在多个算例中减少近30%，因此CRO算法更适合于实时调度，将CRO与基于扩展节约法的集合覆盖算法(SetCovering Based Extended Savings Algorithm, SC-ESA)、粒子群优化(Particle Swarm Optimization, PSO)算法、带局部搜索的差分进化算法(Differential Evolution algorithm with Local Search, DELS)[19]几种常用算法进行对比，比较结果如表5所示，表中RPD为相对差异百分比，

(18)

式中：fCRO为本算法的最优解，fmin为其他算法的最优解。

表5 CRO与其他算法结果比较

由表5可知，CRO算法的9个案例中有2个案例的求解结果优于SC-ESA，总体结果与SC-ESA相近，略差于经典的PSO，DELS算法，但也有近50%的案例结果与PSO，DELS算法相同，平均解偏差不超过1.5%，因此证明CRO算法具有较强的搜索能力。

表6 CRO算子的实验结果

图12和图13所示分别为应用CRO算法得到的表2中案例2的线路图和收敛图。由图13的收敛图可知，算法初始阶段，由于α较小、β值较大，合成、分解反应发生的概率较高，目标函数值减小的幅度较大；随着迭代次数的增加，α逐步增大，β值逐步减小，合成、分解反应发生的概率降低，目标函数值降低的幅度变小。

5 结束语

本文将CRO算法应用于CVRP，主要进行了以下研究：

(1)将CRO算法的分子设计为反映顾客与配送中心序列的实数码，借鉴GA的交叉、变异和局部优化方法对CRO算法的撞墙、分解、合并和交换4个反应进行设计。具体为在撞墙反应中采用互换变异操作，分解反应中采用循环交叉操作，将单条路径分解为带有母体部分特征的两条路径，以扩大解的搜索范围；交换反应采用次序交叉操作，借鉴局部优化思想设计合成反应，在合成反应过程中获得局部路径最小解。

(2)采用动态方式设置CRO算法的两个重要参数α和β，将全局搜索与局部搜索有效结合，获得了较强的搜索能力。将求取的解与标准benchmark的6个P类和3个A类案例进行对比，结果显示CRO算法能够很好地求解CVRP，绝大多数结果与标准库的数据误差不超过5%，但其CPU用时减少幅度较大。随着实时配送对顾客满意度影响的增大，在不增加或少增加配送成本的基础上，增大配送实时性有助于提高顾客满意度，由此证明CRO算法是一种求解CVRP的有效算法。

下一步主要研究将CRO算法应用于带时间窗的车辆路径问题、动态车辆路径问题(Dynamic Vehicle Routing Problem, DVRP)等其他类型的VRP中，进一步拓展CRO算法的应用范围。