箭体结构连接刚度影响因素研究

李 操 商显扬 周 鑫 冷 月

北京宇航系统工程研究所，北京，100076

0 引言

火箭箭体由若干个舱段或部件组成，各部件之间有一些对接面，通过对接面上的连接件将部件连成一个整体。通常，箭体各舱段之间采用箭体连接结构，用螺栓进行连接。典型的螺接方式是将两个组件的对接面，用沿组件周向分布且与外框缘平行的螺栓（也可以是螺钉、销钉等连接件）连接固定。这种连接方式使组件连接面上的作用内力包含剪力、弯矩、轴向压力。连接面上的内力由螺栓受拉和对接框的部分端面受挤压来传递。轴向压力由连接框的端面受压来传递。部件间的剪力传递因存在对接面之间的摩擦而比较复杂。当剪力大于摩擦力时，部分螺栓才承受剪力的作用。这种螺栓连接结构的对接面对整个箭体的刚度影响较大［1⁃3］。

螺栓连接面的结构刚度特性较为复杂，同时受到预紧力、对接件厚度、螺栓分布、载荷等外界因素的影响，使得结构受力状况也很复杂。本文针对以上几个影响因素进行研究，运用有限元法以及软件进行计算仿真，研究结构刚度和固有特性，连接螺栓预紧力的施加方法，最佳预紧力的确定以及对接件厚度、螺栓分布等外部因素对连接结构刚度和固有特性的影响［4］。

1 连接结构特性影响因素理论分析

1.1 螺栓连接预紧力分析

在螺栓连接中，过大的预紧力会导致螺纹连接零件静力破坏、被连接件滑移、分离或紧固件松脱等；过小的预紧力会导致螺栓疲劳破坏、设备质量增大和成本提高。由此，预紧力的大小十分重要，预紧力的控制是螺栓连接中的重要问题之一［5］。

1.1.1 预紧力分析计算

根据已有的理论分析，螺栓的总拉力除了和预紧力Qp、工作拉力F有关外，还受到螺栓刚度Cb及被连接件刚度Cm等因素的影响。根据材料力学的变形关系可知：从螺栓连接的受力与变形的关系入手，进行预紧力与工作载荷总拉力的分析计算是可行的［6⁃7］。

一般情况下，螺栓的总拉力F0并不等于螺栓所受拉力F′与工作拉力F之和。当应变在弹性范围之内时，单个零件的受力可根据静力平衡和变形协调条件求出。

由图1可知，根据静力平衡条件，螺栓所受拉力应与被连接件所受压力大小相等，均为F′，螺栓伸 长 量 δ1=′/Cb，被 连 接 件 缩 短 量δ2=F′/Cm。这时，螺栓拉力增量为F0-F′，伸长增量为Δδ1；被连接件放松时，它所受压力减小为残余预紧力F''，压力减量为F′-F″，缩短减量为Δδ2。根据螺栓的静力平衡条件可得

F0=F+F″ （1）

根据螺栓与被连接件变形协调条件，有Δδ1=Δδ2，

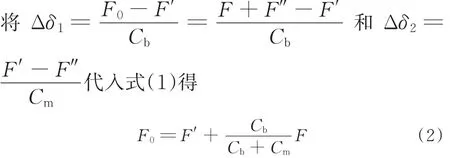
图1 螺栓和被连接件的力与变形量的关系Fig.1 The relationship of force and deformation between b lot and the structure

1.1.2 预紧力与预紧力矩的理论关系

拧紧螺母时，需克服螺旋副间的螺纹力矩T1和螺母支撑面上的摩擦力矩T2，故拧紧力矩

式中，γ为螺纹角；d2为螺纹中径；d0螺纹孔直径；D0为螺母环形支撑面外径；d为螺纹公称直径；φν为当量摩擦角;fc为螺母与支撑面间的摩擦因数。

对于 M 10～M 68 粗牙螺纹，γ ∈ 1°42'～3°2'，d2≈ 0.9d，d0≈ 1.05d，D0≈ 1.6d，φν≈arctan1.55f（无润滑时，螺纹副滑动摩擦因数f≈0.1～0.2），fc≈ 0.15。

整理后可得螺栓预紧力与预紧力矩的近似关系式：

1.2 螺栓连接中对接件厚度分析

根据几何尺寸对拉伸刚度的影响，螺栓连接结构的受力变形中可以利用胡克定律来定义拉伸刚度：

式中，k为拉伸刚度；ΔF为轴向拉力的增量；Δx为ΔF作用下安装边缘节点平均位移的增量。

根据相关资料，当两被连接件的材料与厚度均相同时，推导出的被连接件总刚度

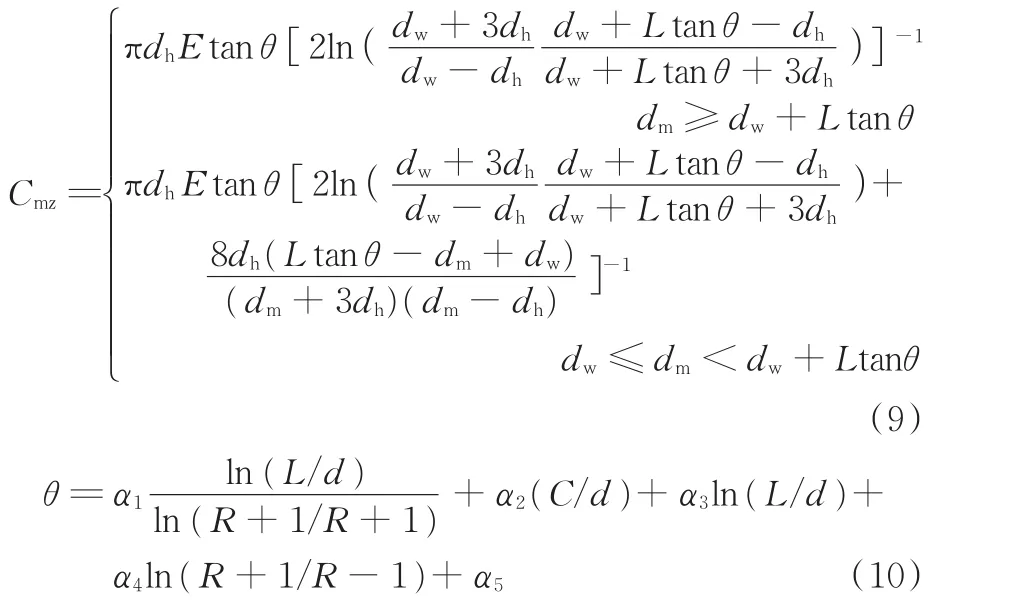
式 中 ，α1=2.5°，α2=-14°，α3=2°，α4=-0.2°，α5=30°；dn为螺栓直径；dw为压紧区域外径；dm为压紧椎体最大直径；L为连接组件厚度；E为弹性模量；θ为半顶角；L/d为相对总厚度；C/d为相对间隙，C为间隙；R为被连接件厚度比。

根据以上公式可知，被连接件刚度与被连接件厚度近似为正比关系，因此，被连接件越厚，其刚度越大，但考虑到火箭箭体的自身质量以及连接件标准，应将对接件厚度控制在合理范围之内。根据以往设计经验，初步将火箭箭体壁厚以及对接件厚度定为6 mm，作为仿真设计的原始参考数据。在进行仿真时，以此厚度值作为参考，对对接件厚度比进行仿真分析。

2 结构动态特性研究

法兰盘上均匀分布Z个M 12螺栓，材料为30CrM nSiA；对接件厚度为6 mm，材料为2A 14。在实际工程应用中，火箭箭体有3.35m、5m、9m三种不同直径，本文仅对直径为3.35 m的火箭箭体连接结构进行分析。在ANSYS中采用参数化建模的方法，建立螺栓、法兰盘A及法兰盘B的几何模型，对箭体及条件变量进行修改。为提高计算精度和效率，进行网格划分时尽可能使螺栓和法兰盘网格对应。螺栓和A、B两法兰盘之间为非线性接触，将法向接触刚度作为有限元分析的重要参数。对法兰盘A的自由边施加约束条件，使其在6个自由度方向均受到约束。约束法兰盘A截面，同时在法兰盘B自由端截面施加集中力载荷及弯矩，利用ANSYS软件计算自由端截面的位移和拉弯耦合刚度，分析预紧力、螺栓分布和对接件厚度及其上下厚度比对箭体连接结构拉弯耦合刚度的影响。连接结构有限元模型见图2。

2.1 螺栓预紧力对连接结构拉弯耦合刚度的影响

图2 连接结构有限元模型Fig.2 Finite elementmodel of connection structure

在法兰结构的圆周上均布36（由下文求得的最佳数目）个M 12螺栓，对螺栓所施加的预紧力设置7种情况，初始预紧力设为15 444 N，在火箭箭体直径为3.35 m情况下进行仿真。为研究连接体的拉弯耦合刚度，首先在对接面施加沿X轴负方向的集中力，载荷剪切力为FY，同时在A筒内侧上施加FX的轴向均布力，计算得到B筒自由端的位移和结构刚度。连接结构拉弯耦合刚度随螺栓预紧力的变化情况见表1。

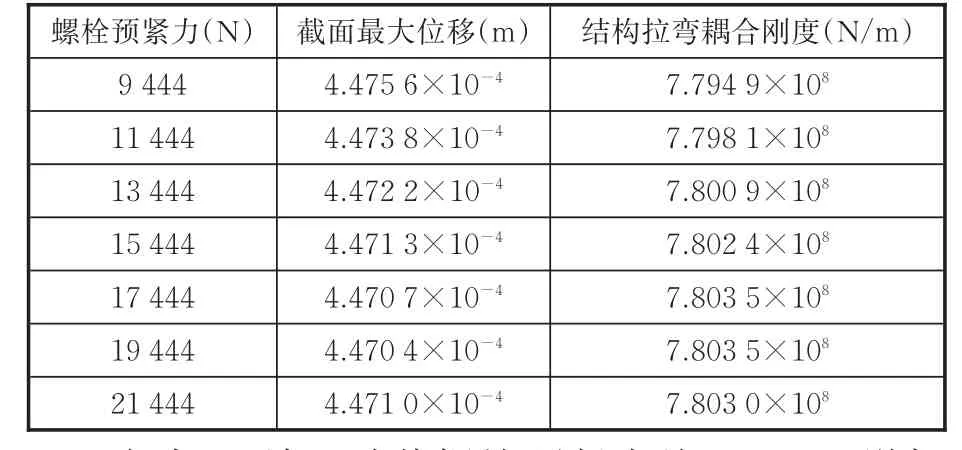
表1 拉弯耦合刚度随螺栓预紧力变化情况Tab.1 In fluence of bolt p re-tigh ting force to flange stiffness

由表1可知，随着螺栓预紧力从9 444 N增加到21 444 N，螺栓连接结构拉弯耦合刚度逐渐增大，达到19 444 N时开始减小。当螺栓预紧力达到19 444 N时，螺栓结构拉弯耦合刚度达到最大值，为7.803 5×108N/m，因此在实际工程中，应适当增大栓预紧力，这样可以在同等螺栓数量下使螺栓连接结构的拉弯耦合刚度最大。

螺栓预紧力为19 444 N时箭体连接结构截面位移情况见图3。

图3 螺栓预紧力为19 444 N时箭体连接结构截面位移Fig.3 Disp lacem en t of connection structu rew ith the bolt p re-tighting force is 19 444 N

2.2 对接件厚度及厚度比对连接结构拉弯耦合刚度的影响

2.2.1 对接件厚度对连接结构拉弯耦合刚度的影响

在螺栓截面施加19 444 N的预紧力，并且对对接面施加沿X轴负方向的集中力，载荷剪切力为FY，同时在对接面上施加FX的均布力。更改法兰盘被连接部分的厚度，设定初始对接件厚度为6 mm，分别设计7种不同厚度值，利用有限元分析软件计算B筒自由端的位移。计算得到的截面最大位移和结构刚度结果见表2。

表2 拉弯耦合刚度随对接件厚度值变化情况Tab.2 In fluence of connection structure dimension to flange stiffness

由表2可以看出，随着对接件厚度从4.5 mm增加到5.0 mm，螺栓连接结构的拉弯耦合刚度逐渐增大，但随着对接件厚度的继续增加，连接结构的整体刚度却不断下降。这与上文中公式推导不符合，可能原因是在仿真中需要模拟较为复杂的工况，而公式推导中并没有考虑复杂工况。根据此仿真结果，在对接件厚度为5 mm时刚度达到7.978 9×108N/m。由此，在实际工程中，应在箭体连接结构结构强度允许的范围内，对接件的厚度值尽可能取较小值，这能保证箭体连接结构拉弯耦合刚度较大，以防止其发生较大的变形而导致安全事故。

对接件厚度值为5 mm时箭体连接结构截面位移见图4。

2.2.2 对接件厚度比对连接结构拉弯耦合刚度的影响

在螺栓截面施加19 444 N的预紧力，并且对对接面施加沿X轴负方向的集中力，载荷剪切力为FY，同时在对接面上施加FX的均布力。更改法兰盘被连接部分的厚度比，设定初始对接件厚度分别为5 mm（根据上文求得最佳厚度值），初始对接件厚度比为1，分别设计7种不同厚度比，利用有限元分析软件计算B筒自由端的位移。计算得到的截面最大位移和结构刚度结果见表3。

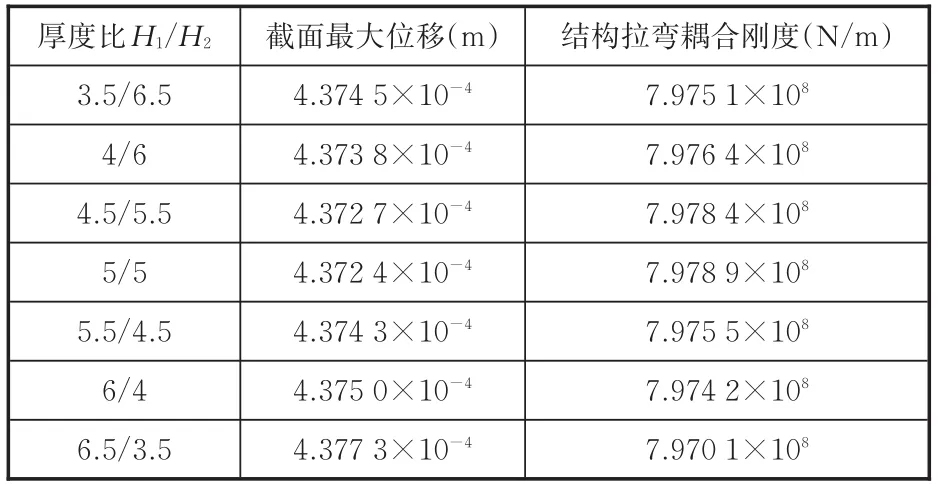
表3 拉弯耦合刚度随对接件厚度比变化情况Tab.3 Influence of connection structu re thickness ratio to flange stiffness

随着对接件厚度比的不断增加，整个连接结构的刚度变化呈现先增大后减小的趋势。其中，在厚度比为5/5时整个箭体结构刚度达到最大，为7.978 9×108N/m。由此，在实际工程中，在箭体连接结构结构强度允许的范围内，对接件的厚度比应尽可能取1，也就是上下对接件厚度应该相同，以保证箭体连接结构拉弯耦合刚度。

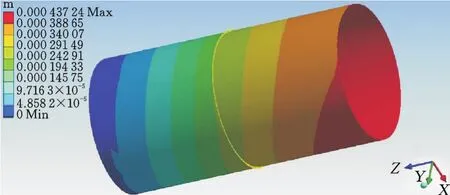
对接件厚度比为1（5/5）时箭体连接结构截面位移见图5。

2.3 螺栓分布对连接结构拉弯耦合刚度的影响

在螺栓截面施加15 444 N的预紧力，设定对接件厚度为5mm、厚度比为1，并且在对接面施加沿X轴负方向的集中力，载荷剪切力为FY，同时在对接面上施加FX的均布力。更改法兰盘螺栓分布数目，设定初始螺栓数目为28，设计7种不同情况的螺栓数目，利用有限元分析软件计算B筒自由端的位移。计算得到的截面最大位移和结构刚度结果见表4。

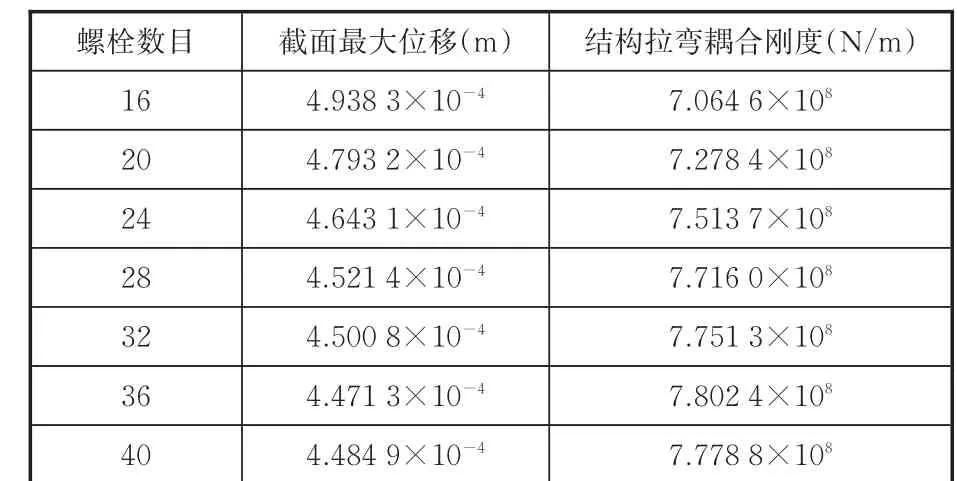
表4 拉弯耦合刚度随螺栓数目变化情况Tab.4 In fluence of bolt am ount to flange stiffness

由表4可知，随着螺栓数目从16增加到36，螺栓连接结构拉弯耦合刚度逐渐增大。当螺栓数目达到36时，此时螺栓结构拉弯耦合刚度达到最大值，为7.802 4×108N/m；而随着螺栓数的继续增加，拉弯耦合刚度开始减小。由此，在实际工程中，对此箭体连接结构采用36颗螺栓圆周均布最佳，以使螺栓连接结构的拉弯耦合刚度最大。

3 结构振动特性影响分析

在对接面施加均布载荷，并且在对接面施加集中力载荷，约束A筒自由端截面。利用AN⁃SYS软件分析箭体连接结构振动特性，讨论预紧力、对接件厚度和螺栓分布对箭体连接结构振动频率的影响。

3.1 螺栓预紧力对箭体连接结构振动频率的影响

选择7种不同预紧力、螺栓数目一致、对接件厚度为5mm、厚度比为1的实验工况，计算在不同螺栓预紧力下简化箭体连接结构的前6阶振动频率，结果见表5。

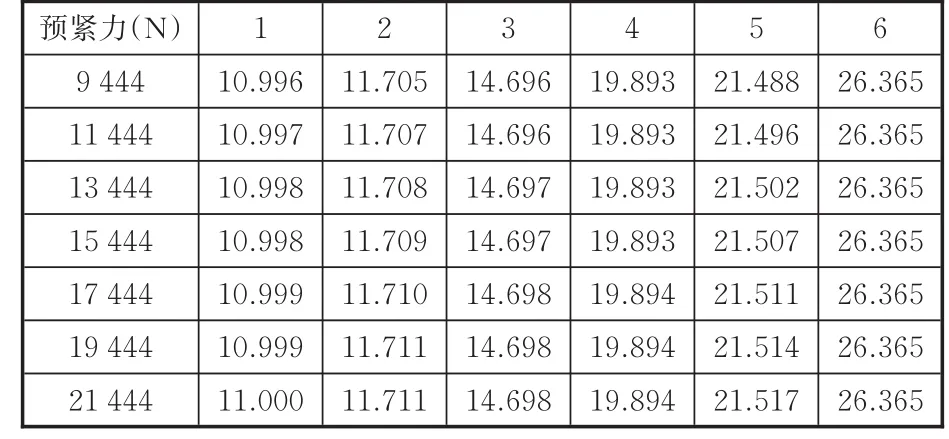
表5 不同螺栓预紧力下连接结构前6阶振动频率Tab.5 The first 6 order vib ration frequencies of the connection structure under the p re-tightening force of d ifferen t bolts Hz

3.2 对接件厚度及厚度比对箭体连接结构振动频率的影响

3.2.1 对接件厚度对箭体连接结构振动频率的影响

选择7种不同对接件厚度值、螺栓数目一致、预紧力为19 444 N、厚度比为1的实验工况，计算在不同对接件厚度下简化箭体连接结构的前6阶振动频率，结果见表6。

表6 不同对接件厚度下连接结构前6阶振动频率Tab.6 The first 6 order vib ration frequencies of the connection structu re under the differen t thickness Hz

3.2.2 对接件厚度比对箭体连接结构振动频率的影响

选择7种不同对接件厚度比、相同螺栓数目、预紧力为19 444 N、厚度值为5 mm的实验工况，计算在不同对接件厚度比下简化箭体连接结构的前6阶振动频率，结果见表7。

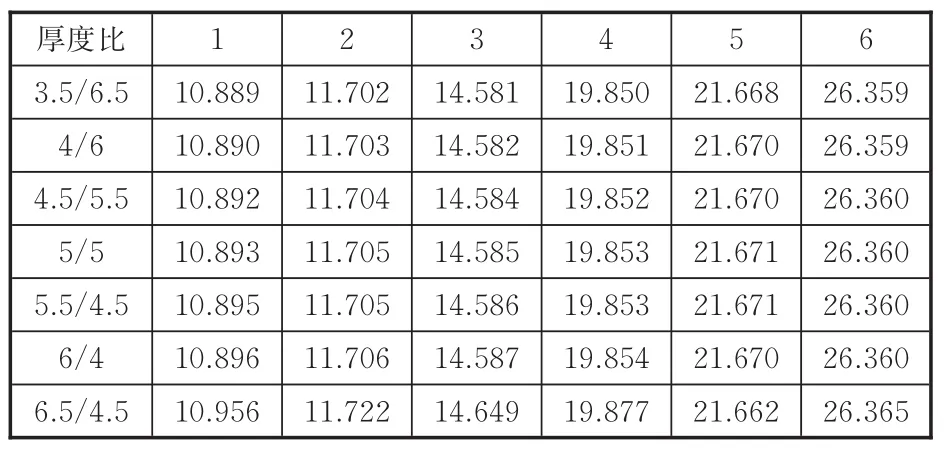
表7不同对接件厚度比下连接结构前6阶振动频率Tab.7 The first 6 order vib ration frequencies of the connection structure under different thickness ratios Hz

3.3 螺栓分布对箭体连接结构振动频率的影响

选择7种不同螺栓数目、预紧力为15 444 N、对接件厚度为5mm、厚度比为1的实验工况，计算在不同螺栓数目下简化箭体连接结构的前6阶振动频率，结果见表8。

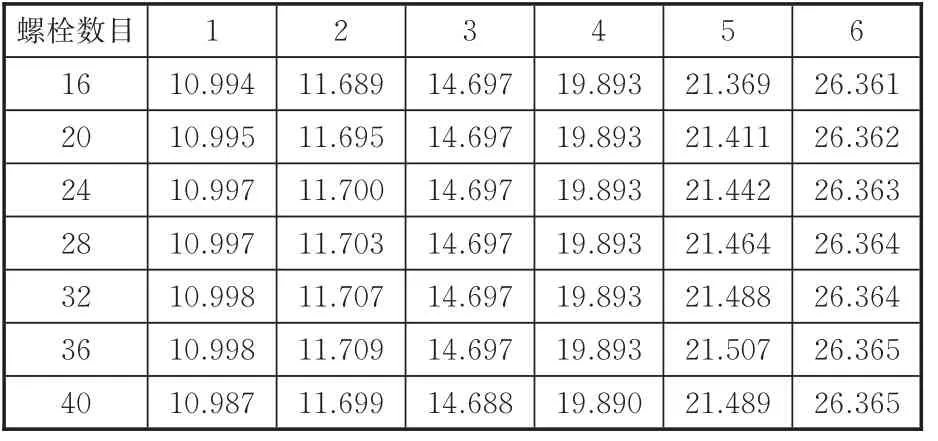
表8 不同螺栓数目下箭体连接结构前6阶振动频率Tab.8 The first 6 order vib ration frequencies of the connection structure under d ifferen t bolt am ounts Hz

4 结论

（1）随着螺栓预紧力从9 444N增加到21 444N，螺栓连接结构拉弯耦合刚度逐渐增大，达到19 444N时开始减小，呈现先增大后减小的趋势。在实际工程中，适当增加螺栓预紧力，可以在同等螺栓数目下使螺栓连接结构的拉弯耦合刚度最大。

（2）随着对接件厚度从4.5 mm增加到5 mm，螺栓连接结构的拉弯耦合刚度增大，但随着对接件厚度的继续增加，连接结构的整体刚度却不断减小。这与文中公式推导不符，可能原因是在仿真中需要模拟较为复杂的工况，而公式推导中并没有考虑在内。在实际工程中，应在箭体连接结构结构强度允许的范围内，对对接件的厚度值取尽可能较小值，以保证箭体连接结构结构拉弯耦合刚度较大，防止其发生较大的变形而导致安全事故。

（3）随着对接件厚度比的不断增大，整个连接结构的刚度变化呈现先增大后减小的趋势。在实际工程中，在箭体连接结构强度允许的范围内，对接件的厚度比应尽可能取1，也就是上下对接件厚度应该相同，以保证箭体连接结构结构拉弯耦合刚度。

（4）随着螺栓数目从16增加到36，螺栓连接结构拉弯耦合刚度逐渐增大。当螺栓数目达到36时，螺栓结构拉弯耦合刚度达到最大值，而随着螺栓数的继续增加，拉弯耦合刚度开始减小。在实际工程中，对此箭体连接结构采用36颗螺栓圆周均布最佳，此时螺栓连接结构的拉弯耦合刚度最大。

(编辑 袁兴玲)