OPTIMAL ERROR ESTIMATES OF A DECOUPLED SCHEME BASED ON TWO-GRID FINITE ELEMENT FOR MIXED NAVIER-STOKES/DARCY MODEL∗

Yi QIN(秦毅)Yanren HOU(候延仁)

School of Mathematics and Statistics,Xi’an Jiaotong University,Xi’an 710049,China

E-mail:qinyi1991@stu.xjtu.edu.cn;yrhou@mail.xjtu.edu.cn

Abstract Although the two-grid finite element decoupled scheme for mixed Navier-Stokes/Darcy model in literatures has given the numerical results of optimal convergence order,the theoretical analysis only obtain the optimal error order for the porous media flow and a non-optimal error order for the fluid flow.In this article,we give a more rigorous of the error analysis for the fluid flow and obtain the optimal error estimates of the velocity and the pressure.

Key words Navier-Stokes equation;Darcy’s law;two-grid method;optimal error estimate

1 Introduction

The Stokes-Darcy model was extensively studied in recent years due to its wide range of applications in many real world problems and industrial settings,readers can refer to[1–8]for more details.Recently the more physically valid Navier-Stokes/Darcy model attracted scientists’attention,and several coupled finite element methods were studied for it[9–14].

We know that Cai,Mu and Xu proposed a two-grid finite element based decoupled algorithm for the Navier-Stokes/Darcymodel in[9],the numerical results show that the convergence orders of the velocity and the pressure in the fluid flow region and the piezometric head in the porous media flow region are all optimal with proper configuration of the coarse and fine mesh sizes,but only an optimal error estimate for the piezometric head in the porous media flow region was obtained,for the velocity and the pressure in the fluid flow region,the estimates are half order lower than the optimal one.Hou gave the optimal error estimates for the Stokes-Darcy model in[15].In this article,we try to use the similar method to give the optimal error estimates for the Navier-Stokes/Darcy model.

The rest of the paper is organized as follows.In Section 2,we introduce the Navier-Stokes/Darcy model with the Beavers-Joseph-Saffman interface condition.The two-grid decoupled scheme proposed in[9]is presented in the next section.In Section 4,we give the main result that is the optimal error estimates for the velocity and the pressure in the fluid flow region.

2 Mixed Navier-Stokes/Darcy Model

We consider a coupled fluid and porous media flows on a domain Ω⊂Rd,consisting of a fluid region Ωfand a porous media region Ωpseparated by an interface Γ,as shown in Figure 1,where d=2 or 3,Ω=Ωf∪Ωp∪Γ,and Γ=Ωf∩Ωp,Γ is assumed to be smooth enough as in[14].Let nfand npdenote the unit outward normal directions on ∂Ωfand ∂Ωp.Now we give the mixed Navier-Stokes/Darcy model:

Figure 1 A global domain Ω consisting of a fluid region Ωfand a porous media region Ωpseparated by an interface Γ

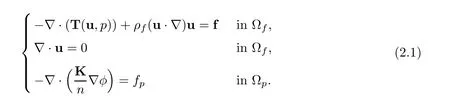
We decompose∂Ωp/Γ into two segments∂Ωp,Dand ∂Ωp,N,and note∂Ωf,D= ∂Ωf/Γ,now impose homogeneous boundary conditions

and the interface conditions on Γ:

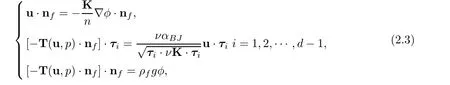
here ρfis the density of the fluid flow,u is the velocity vector,p is the pressure, φ is the piezometric head,f is the external force,and fpis the source term due to injection or pump,

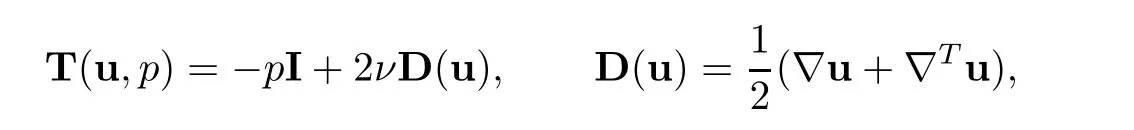
ν>0 is the kinetic viscosity,n is the volumetric porosity,g is the gravity acceleration,and K is the hydraulic conductivity tensor of the porous media satisfying

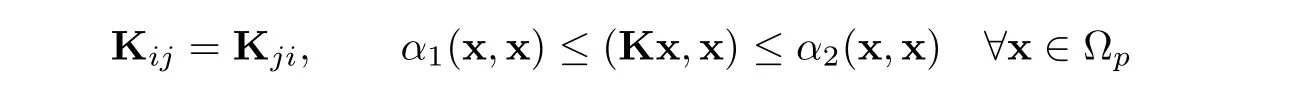
with positive constants α1and α2.are linearly independent unit tangential vectors on Γ,and αBJis an experimentally determined positive parameter.The first interface condition ensures mass conservation across Γ.The second one,known as the Beavers-Joseph-Saffman law,states that the slip velocity along Γ is proportional to the shear stress along Γ [14,16–21].The third one is the balance of normal forces across the interface.

Following the terminology in[9],let us denote

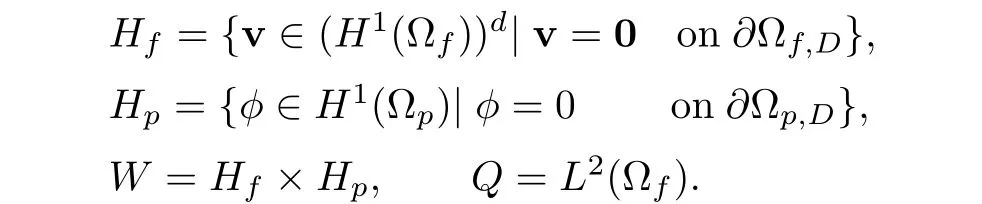
The corresponding weak formulation of the coupled Navier-Stokes/Darcy model reads as follows:given f=(f,fp), find u=(u,φ)∈ W,p∈ Q such that

and

a(w;u,v)=aSD(u,v)+af,c(w;u,v)≡ (af(u,v)+ap(φ,ψ)+aΓ(u,v))+af,c(w;u,v)with

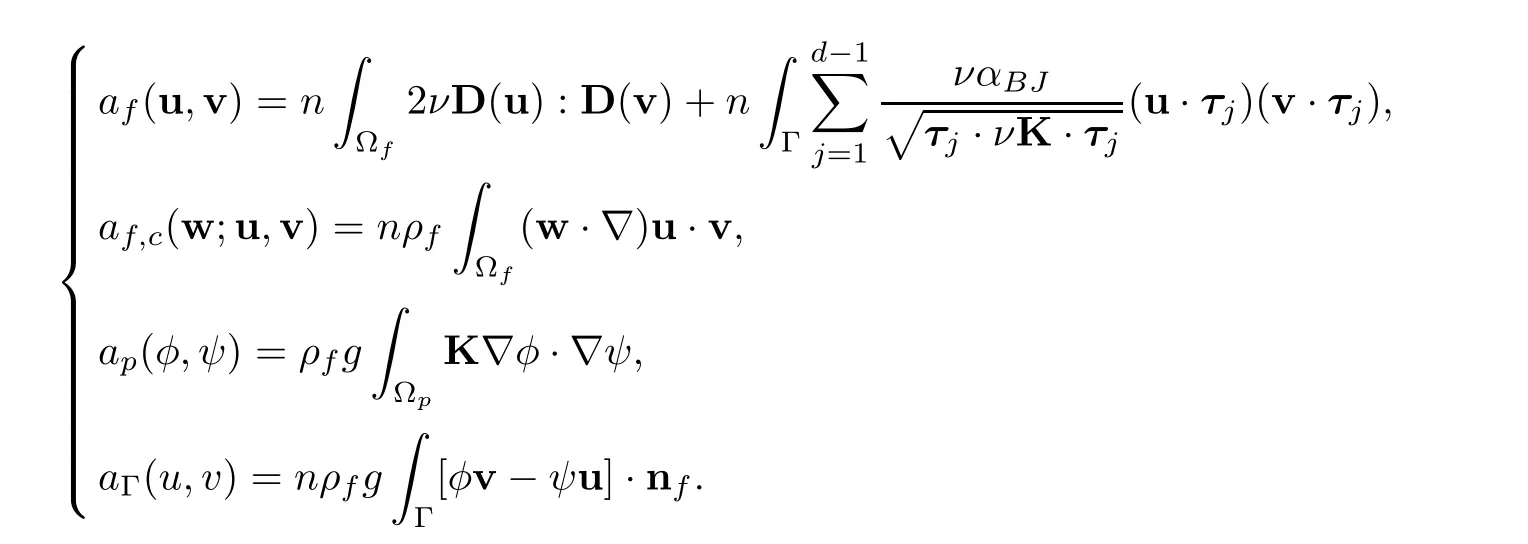
Note that,

i)aSD(u,v)≡ af(u,v)+ap(φ,ψ)+aΓ(u,v)is the corresponding bilinear form in the linear coupled Stokes-Darcy problem[6,16];

ii)|af,c(w;u,v)|≤ CkD(w)kL2(Ωf)kD(u)kL2(Ωf)kD(v)kL2(Ωf),where C is a constant that depends on the model parameters only[14,22];

iii)the inf-sup condition holds[14,23,24]

3 Two-Grid Decoupled Scheme

Let Hf,h×Qh⊂ Hf×Q be a stable finite element space in Ωf,and let Hp,h⊂ Hpbe a conforming finite element space in Ωp,denote Wh=Hf,h×Hp,h.We assume that the following discrete inf-sup condition holds[14,17]

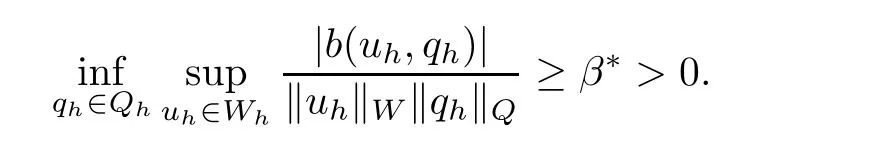
We also assume that the local regularity

Then the finite element spaces have the following approximation properties:there exists( euh, eph,)∈Hf,h×Qh×Hp,hsuch that

A coupled algorithm for the Navier-Stokes/Darcy model reads: find uh=(uh,φh)∈ Wh,ph∈Qhsuch that

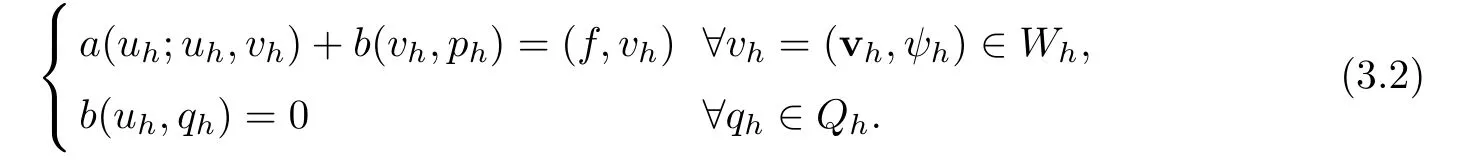
Now we state the two-grid algorithm proposed in[9]as follows.

1.Solve problem(3.2)with a coarse mesh size H>h: find uH=(uH,φH)∈ WH⊂ Wh,pH∈QH⊂Qhsuch that

2.Solve two decoupled and linear local problems on a fine grid: find φh∈ Hp,hsuch that

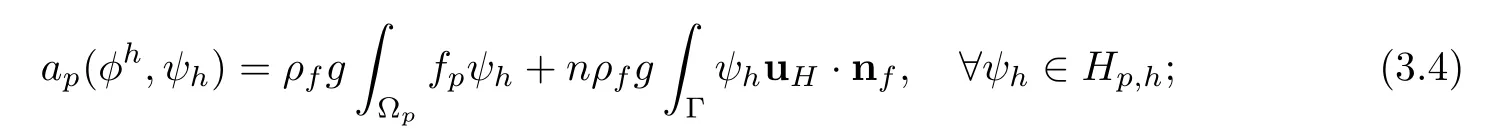
find(uh,ph)∈Hf,h×Qhsuch that

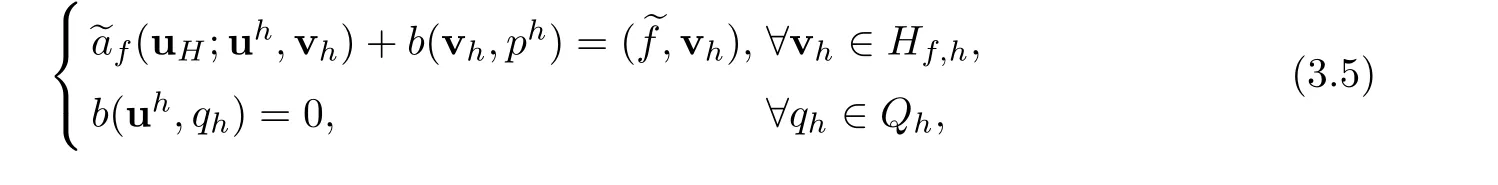
where

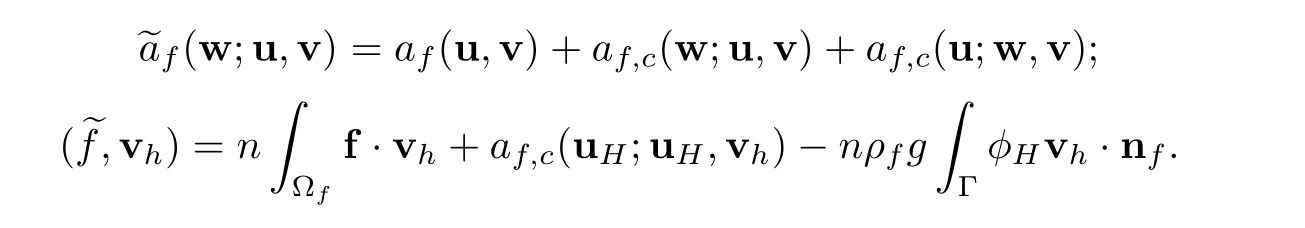
4 Optimal Error Estimates

In[9],the authors applied the Mini elements[27,31,32]in the fluid region and the piecewise linear elements in the porous media region and obtained the following error estimates when h=H2:

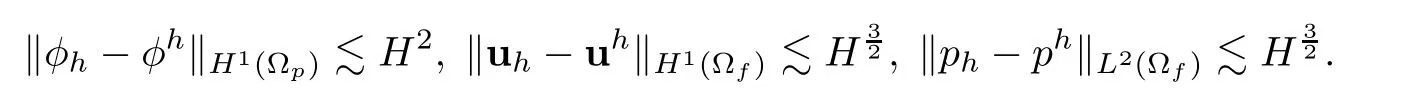
And they also claim that the error estimates in the fluid region should be half order higher than the estimates obtained.

The king looked on for a little, and then returned with his attendants to the palace, reflecting all the while on the extreme lightness of his proposed bride and the absurdity10 of having a wife that rose in the air better than any kite

Now we give the main result that is the optimal error estimates for the velocity and the pressure in the fluid flow region.

Theorem 4.1 Let uh,phand uh,phbe defined by the two discrete models.We assume that both Ωfand Ωpare smooth domains and the source terms are all square integrable in corresponding domain such that the mixed Navier-Stokes/Darcy problem satisfies the local regularity assumption.Then there hold the following optimal error estimates

Proof Estimate(4.1)was obtained in[9]already.For the estimates of the approximation to the velocity and pressure in the fluid flow region,we introduce an auxiliary problem in the porous media region[15].That is to find Φ ∈ H1(Ωp)satisfies

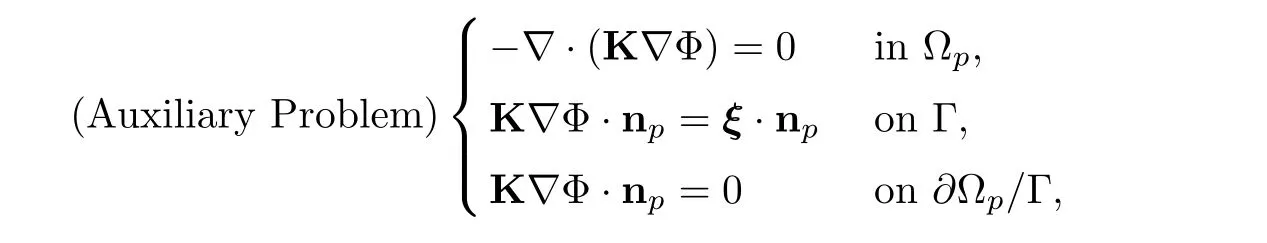
here for any given vh∈ Hf,h,we take ξ =nρfgvh.This auxiliary problem is actually an extension of vh∈ Hf,hinto Ωpto some extend.And we can easily show that

Since Ωpis a smooth domain,we have for vh∈ Hf,

Now subtracting(3.5)from(3.2)yields

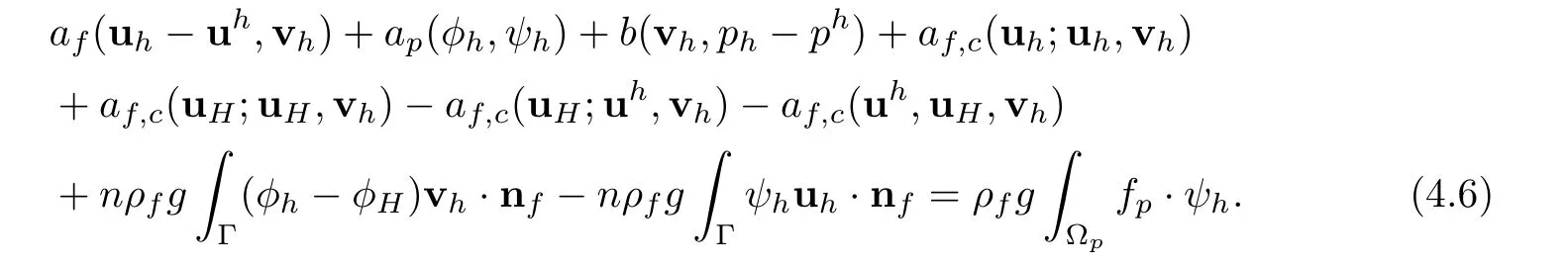
Taking vh=(vh,0)in(4.6),we have

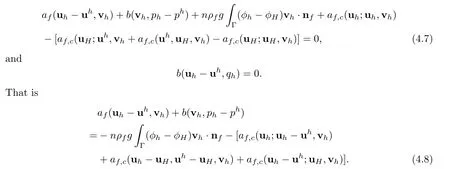
For the first term on the right hand side of(4.8),we have

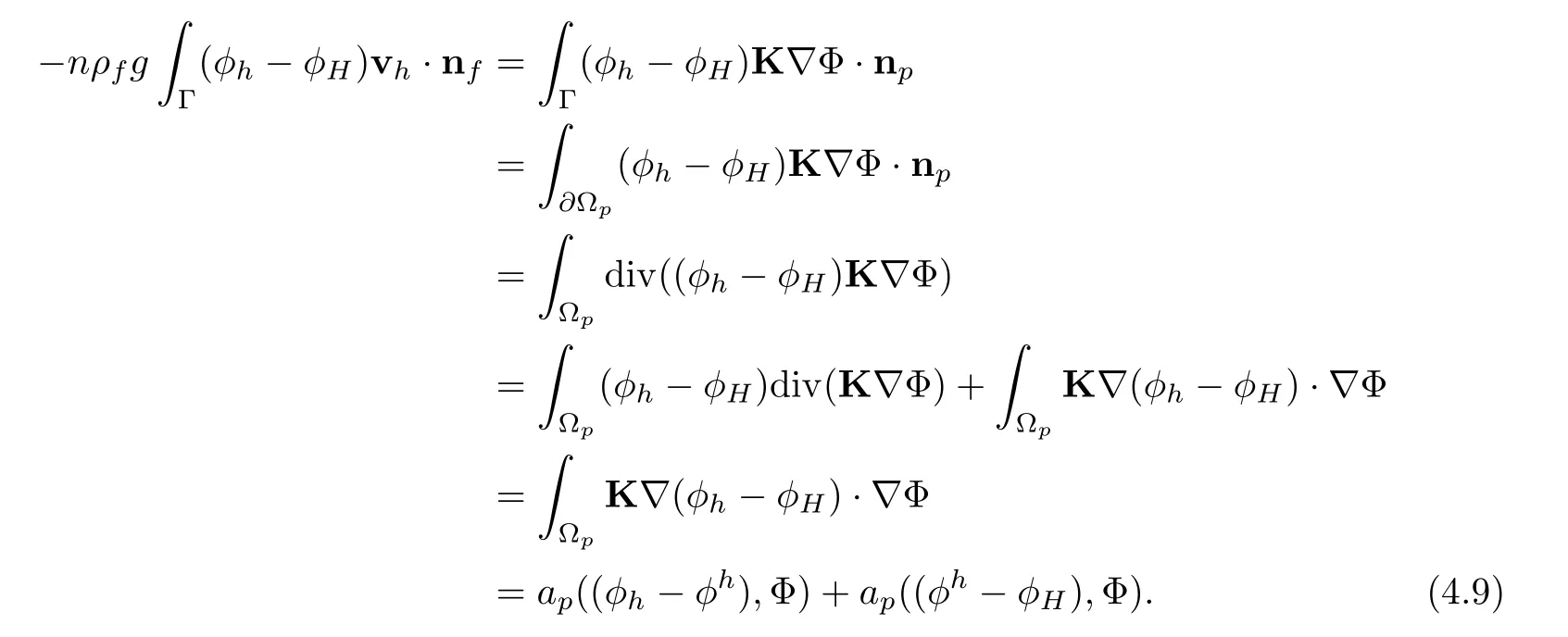
For the second term on the right hand side of(4.9),as we know that

we have

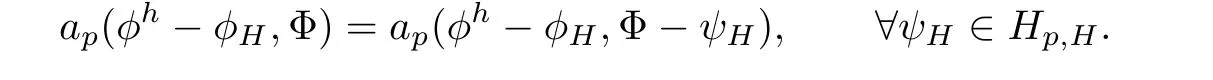
Therefore by using(4.1)and(4.5),we obtain

If we take vh=uh−uhin(4.8),then b(uh−uh,ph−ph)=0 and from the last three terms on(4.8),we have

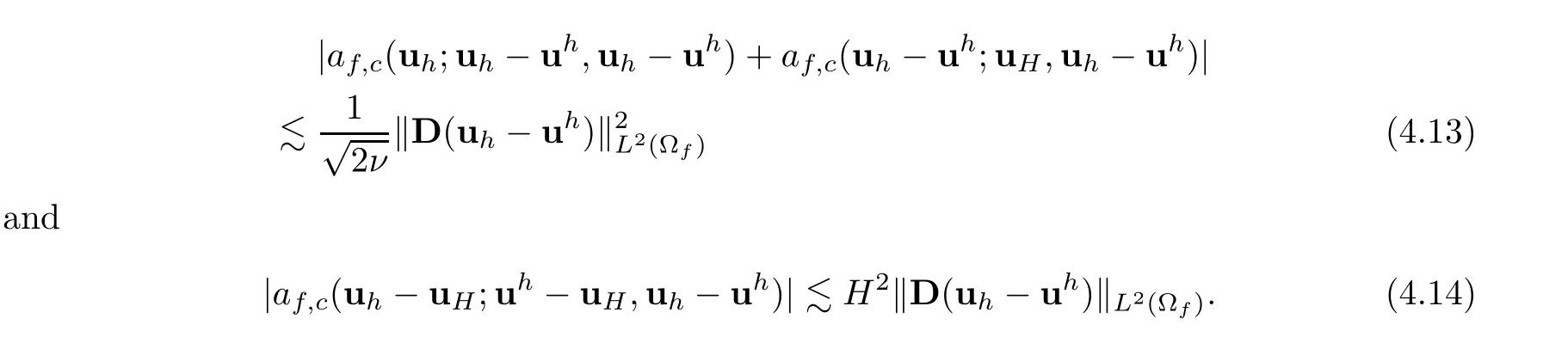
Then by(4.12)–(4.14),we have

Thanks to the coercive property of af(·,·),and the fact that the coupled Navier-Stokes/Darcy model is well-posed if ν is sufficiently large(in fact 2which is shown in[10],we can obtain

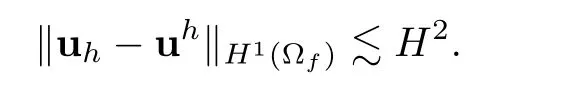
Now let us give the error estimate of the pressure.By the discrete inf-sup condition,we can obtain

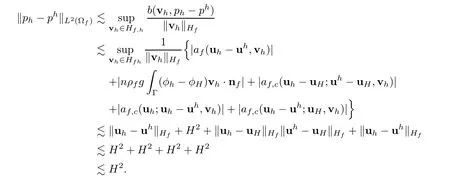
We obtain the results when h=H2.

5 Numerical Experiments

In this section,we shall give a numerical experiment to illustrate our main result that are the optimal error estimates for velocity and pressure in the fluid flow region.We assume that the computational domain Ωf=(0,1)× (1,2)and Ωp=(0,1)× (0,1)with interface Γ =(0,1)× 1.For simplicity,we set the physical parameters g,ν,k and α equal to 1.Thefinite element spaces we used are the well-known Mini elements(P1b−P1)for fluid flow region and linear Lagrangian elements(P1)for porous media region.And the relation for the coarse mesh H and the fine mesh h is chosen as h=H2.Moreover,we apply the software package FreeFEM++to implement the algorithm and all results are generated by the same computer.

We set the exact solution which satisfies Beavers-Joseph-Saffman interface condition and homogeneous boundary conditions is

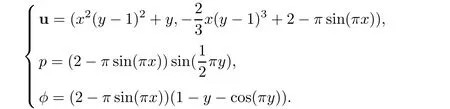
The forcing terms follow the exact solution.

In Table 1,we list the errors between the exact solution and the solutions of the two-grid scheme.And as expected,it also shows that the convergence orders of the velocity and the pressure in the fluid flow region reach the first order for h,which coincide with our theoretical results in Theorem 4.1.In Table 2,we give the computational time of the coupled finite element scheme and the two-grid scheme.“N-S/D”denotes the CPU time spent by the coupled scheme,and “N-S”and “Darcy”denotes the CPU time spent by Navier-Stokes sub-problem and Dacry sub-problem,respectively. “N-S/D(TG)” denotes the total CPU time spent by the two-grid scheme.It shows the two-grid scheme costs less time than the coupled finite element methods.

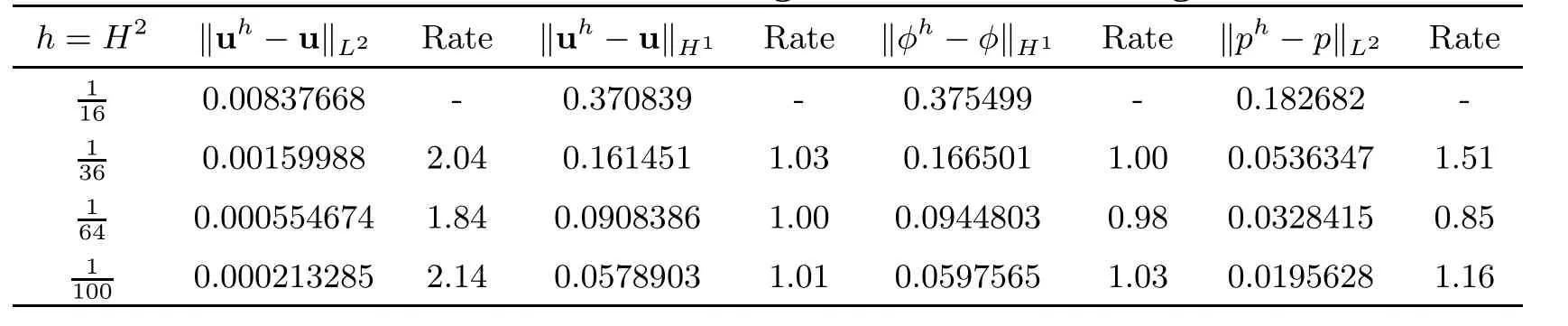
Table 1 The errors and the convergence rates of the two-grid scheme

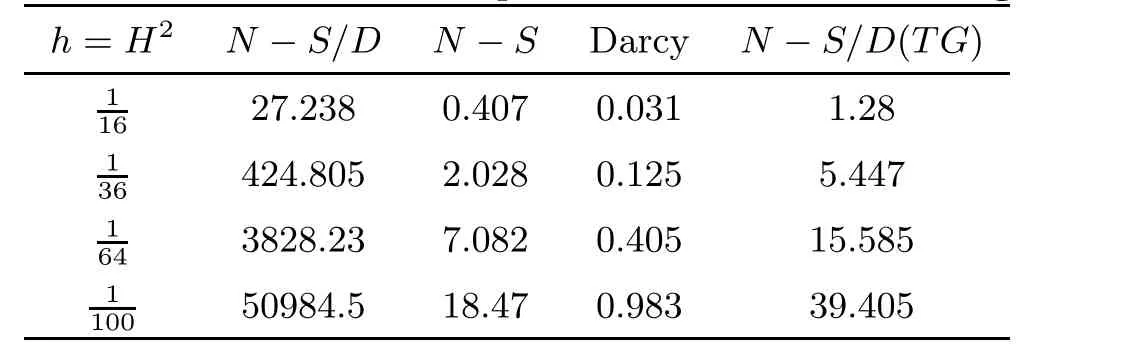
Table 2 The CPU time of the coupled scheme and the two-grid scheme