PARAMETER IDENTIFICATION BY OPTIMIZATION METHOD FOR A POLLUTION PROBLEM IN POROUS MEDIA∗
R.ABOULAICH
LERMA,Ecole Mohammadia d’Ingénieurs Université de Mohammed V-Agdal,Avenue Ibn Sina B.P 765,Agdal,Rabat,Maroc
E-mail:aboulaich@emi.ac.ma
B.ACHCHAB
Université Hassan 1,Ecde Supérieure de Technologic Berrechi,and LAMSAD,ESTB,B.P 218 Berrechid,Maroc
E-mail:achchab@estb.ac.ma
A.DAROUICHI
Université Cadi Ayyad,Ecole Supérieure de Technologie,B.P 383 Essaouira,Maroc
E-mail:azizdarouichi@gmail.com
Abstract In the present work,we investigate the inverse problem of reconstructing the parameter of an integro-differential parabolic equation,which comes from pollution problems in porous media,when the final observation is given.We use the optimal control framework to establish both the existence and necessary condition of the minimizer for the cost functional.Furthermore,we prove the stability and the local uniqueness of the minimizer.Some numerical results will be presented and discussed.
Key words inverse problem;coefficient identification;optimization method;pollution problem;porous media
1 Introduction
In this work we study an inverse problem of identifying the parameter of a time-dependent convection-diffusion integro-differential equation of a pollution problem arising in porous media,when the final observation is given.This type of problem has an important application in the broad field of engineering and applied sciences.This inverse problem consists in determining the initial liquid concentration of a volatile organic contaminant,since we can compute its gaseous concentration at final time T>0.Consider the following contaminant transport system in porous media[2,5,26,28]:

where the subscripts a,w designate the gaseous and water phases of the contaminant,Caand Cw[ML−3]are the corresponding concentrations,εaand θ are the volumetric gaseous and water contents(dimensionless)[L3L−3],vais the velocity of the gaseous phase.The dispersion tensor D[L2T−1],is the standard form(see[3]),KHis Henry’s constant(dimensionless),ksis the first order mass transfer coefficient[T−1],C0aand C0ware the initial concentrations in the gaseous and liquid phases,respectively.The unknowns are the state variables Caand Cw.Physically speaking,this model describes the vapor transport of an organic volatile contaminant in the unsaturated soil zone which is considered as a rigid non deformable porous medium,coupled with the nonequilibrium mass transfer between the gaseous and liquid phases.From equations(1.1)2and(1.1)6,the function Cwwrites under the form
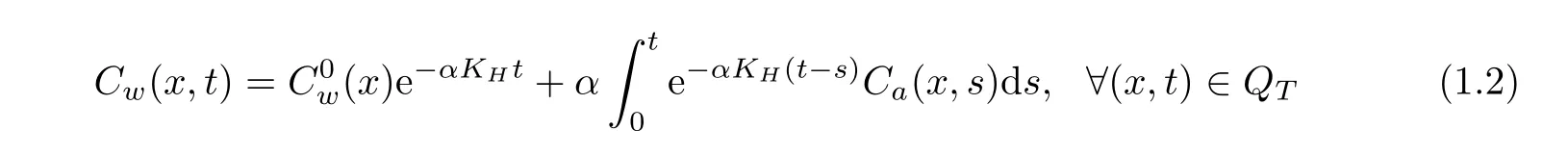

Thence equation(1.1)2is eliminated.Therefore,the inverse problem which we shall consider is the following:for each T>0,if the concentration Caverifies equation(1.3)and conditions(1.1)3–(1.1)5are fulfilled,and moreover if the concentration Ca(·,T)is given,this allows to reconstruct uniquely the pollutant initial liquid concentration
A time independent function should be identified in the right-hand side of equation(1.3).In doing so,we use the following change of variables
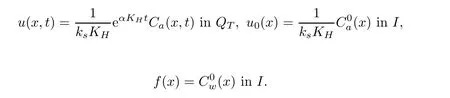
Under these notations,we get

where r=ks−αKHand µ = αksKHwith α =Suppose the following additional condition is given:

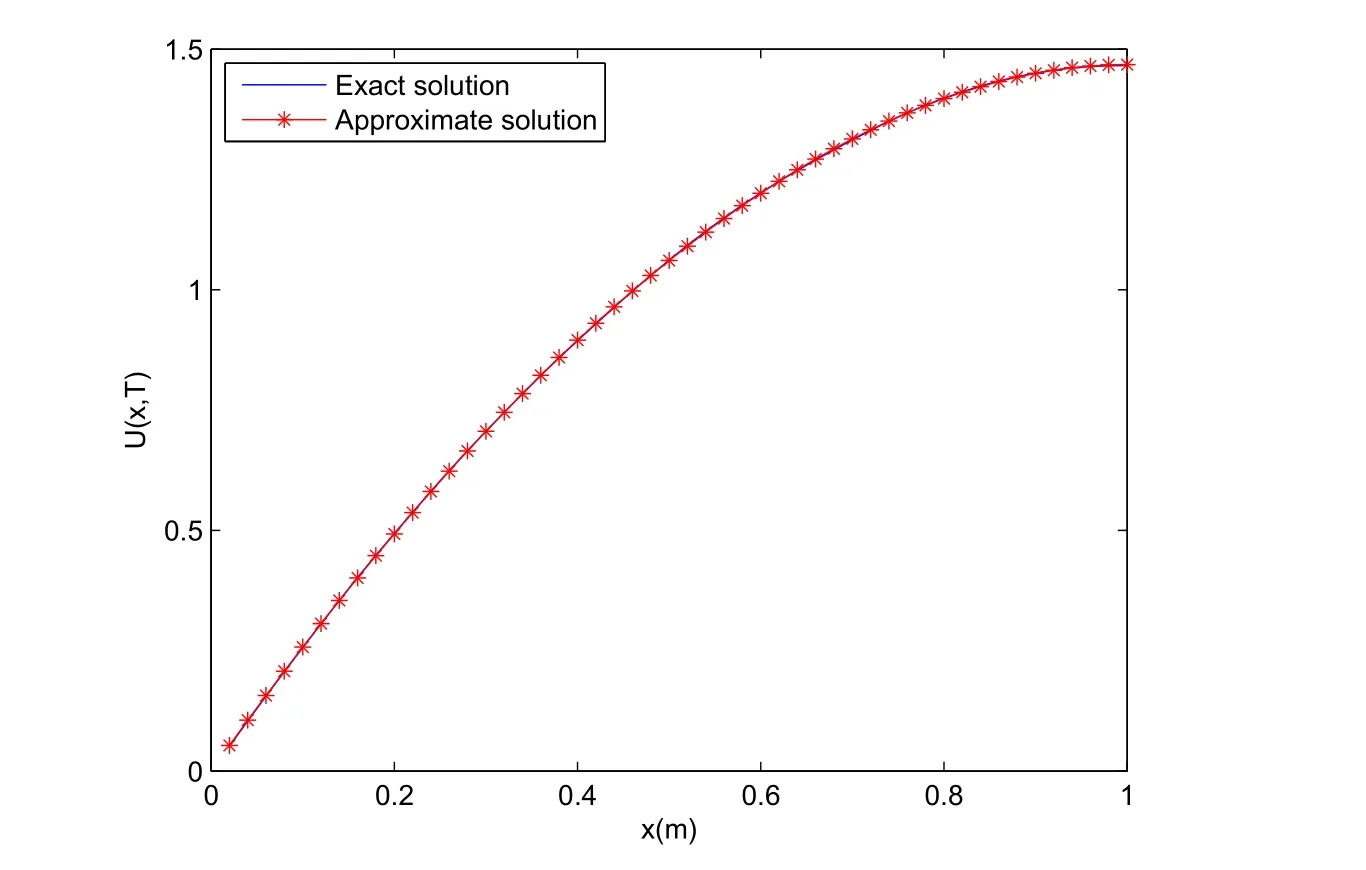
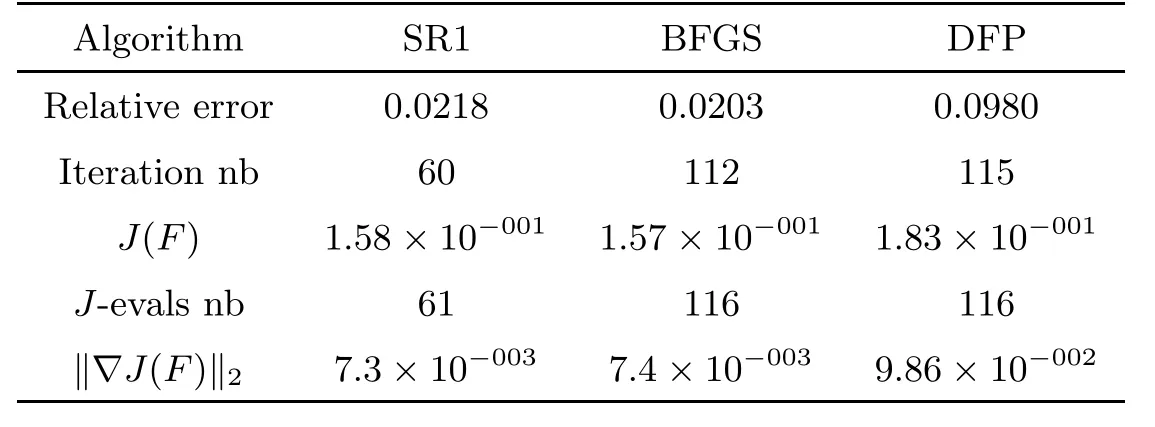
where g is a known function,the terminal status observation is possibly given via the interpolation of the final observation measurements.Find the functions u and f satisfying(1.4)–(1.5).The coefficient f(x)stands for the initial concentration of the pollutant in the liquid phase and g(x)represents the given gaseous concentration of the pollutant at final time T>0 while u represents the gaseous concentration of the pollutant at any time t For a given function f(x),the convection-diffusion integro-differential problem(P)which is referred as a direct(or forward)problem consists of the determination of the pollutant gaseous concentration u from the given initial-boundary conditions.We should point out that there is a principal difference between the direct and the inverse problems.In fact,the direct problem is well-posed while the inverse one is ill-posed or improperly posed in the sense of Hadamard(see[22,24,29]).A mathematical problem is called as well-posed problem if it has the following properties. •There exists a solution of the considered problem(existence). •The problem has at most one solution(uniqueness). • The solution of the problem is depending continuously on the data of the problem(stability). The major requirement is the stability of the problem.If the solution of a problem is not depending on the data of the problem,therefore the calculated solution has no relation to do with the true solution(see for example[20,22,24,25]).The principal difficulty for problem(P)is the numerical instability.It is not so easy to avoid some errors in the final observation u(x,T)that is often gotten by experiments.A small perturbation in the final observation u(x,T)may imply a great change in f,which may render the obtained results not meaningful.We notice that several authors have investigated the inverse parameter problems for time-dependent equations,see for instance[6–9,12,19,22–24,29]among others.However,in the present paper we discuss the inverse coefficient problem of a time-dependent convectiondiffusion-reaction integro-differential equation(P),by using the optimal control framework(see for instance[14–17,23,30,31]),from the theoretical analysis angle.The numerical solution is calculated from the optimality system with which the minimizer of the cost functional must satisfy by using the finite difference method. This paper is structured as follows:in Section 2,the inverse problem(P)is reformulated as an optimal control problem(P)and some prior results for the direct problem are given.The existence of the minimizer of the cost functional is shown in Section 3.In Section 4,the necessary condition for the minimizer is derived.The local uniqueness of the minimizer is derived in Section 5.The stability of the minimizer is obtained in Section 6.In the last section,some numerical results are presented. We propose to reformulate the inverse problem(P)as a constrained least-squares optimization problem.This method is very easy for the computation of the solution f.To do so,we consider the following optimal control problem(P). and u(x,t;f)is the solution of problem(P)for a given f ∈ Uadand ν is the regularization parameter.The first term of the objective functional looks for the mis fit between observed and predicted states.The second term is a regularization with parameter ν and{α0,β0}are two given positive constants. For the additional condition(1.5),we suppose that the function g(x)satisfies g∈L2(0,1). In what follows,k·k2denotes the L2-norm on(0,1)and we introduce also the following spaces Lemma 2.1 Assume that u0(x)∈H1(I).For any given f(x)∈Uad,there exists a unique solution u(x,t)∈W0to equation(1.4). Proof The proof is similar to that presented in[1,11]in two dimensions. ? Lemma 2.2 Assume that u0(x)∈L2(I).For any given f(x)∈L2(I),there exists a nonnegative constant C only depends on T such that Proof By virtue of equation(1.4),we have for 0 This yields Then Owing to Whence This implies, with|r|=abs(r).By applying the Gronwall’s lemma,we get the result.This completes the proof of Lemma 2.2. ? The study of the uniqueness for the inverse problem(1.4)–(1.5)is an important task.Through the uniqueness result,we can await the minimizing sequence from optimization problem effectively tends to the unique classical solution at least in some general sense.We have the following uniqueness result. Theorem 2.3 Suppose that the contaminant initial gaseous concentration u0(x)≥0,u0(x)6=0 in I.Moreover,assume that f1,f2∈Uad.Therefore we have f1(x)=f2(x)if u1(x,T)=u2(x,T). Proof The proof is very long and quite using the similar techniques and arguments as those in[27].For this reason,we leave out the details here. Theorem 3.1There exists a minimizer f∈Uadof J(f),i.e., Proof Let(fn,un)be a minimizing sequence,namely, with unis a solution of problem(P)and fn∈Uad.As fn∈Uad,then fnis bounded in H1(0,1),so there exists a subsequence still denoted fnconverges weakly to f.From[1,Theorem 4.2],we have the following estimate Then We can easily check that( f,u(x,T; f))satisfies(1.4). According to the Lebesgue’s theorem,we deduce Theorem 4.1 Let f be the solution of the optimal control problem(2.1).Then there exists a triple of functions(u,λ;f)satisfying the following system for any h in Uad. Proof For any h∈Uad,0≤δ≤1,we have Then Let uδbe the solution to problem(1.4)with given f=fδ.Since f is an optimal solution,we have In view of(4.5)we obtain where L∗is the adjoint operator of the operator L.In virtue of(4.7)and(4.9),we get Combining(4.8)and(4.10),one can easily obtain that This completes the proof of Theorem 4.1. In this section,we prove the uniqueness result.Assume f1(x)and f2(x)be two minimizers of the control problem(P)and{ui,λi}(i=1,2)be solutions of system(4.1)–(4.2)in which f=fi(i=1,2),respectively. Setting therefore U and Λ satisfy Lemma 5.1 For any bounded continuous function h(x)∈C(0,1),we have where x0is a fixed point in(0,1). Proof We have for 0 This accomplishes the proof of Lemma 5.1. We have the following result. Lemma 5.2 For equation(5.1),we have the following estimate Proof From equation(5.1),we have for 0 Subsequently By using Gronwall’s lemma,we get where CT=e(1+µ)T2.Then for T ≪1 we obtain where C is a nonnegative constant independent of T.This completes the proof of Lemma 5.2.? We have also the following result. Lemma 5.3 For equation(5.2),we have the following estimate Proof From equation(5.2),we have Then By using(5.2)4and(5.3),we get By using Gronwall’s lemma,and using that T ≪ 1 we obtain This completes the proof of Lemma 5.3. We have the following uniqueness result. Theorem 5.4 Assume f1(x),f2(x)be two minimizers of the optimal control problem(P).If there exists a point x0such that therefore for T≪1,we have Proof By taking τ=f2when f=f1and taking τ=f1when f=f2in(4.3),we get with{ui,λi}(i=1,2)are solutions of system(4.1)–(4.2)in which f=fi(i=1,2),respectively. By virtue of(5.5)and(5.6)we obtain From the assumption of Theorem 5.4,there exists a point x0∈(0,1)such that From Lemma 5.1 we obtain By using Hölder’s inequality we get From(5.9),(5.10)and in view of(5.4),we have Choose T≪1 such that Combining(5.11)and(5.12)we can easily obtain that This yields Noticing(5.8)and(5.14),we get This completes the proof of Theorem 5.4. In this section,we will treat the stability of the optimal solution.For the proof of the stability of the minimizer,we will use the following necessary condition(4.1)–(4.7)and(4.8).We assume that the exact final observation g(x)is attainable,i.e.,there exists an f∈Uadsuch that u(x,T;f)=g(x),and that an upper bound δ for the noise level of the observation is known a priori.Let fδ∈Uadbe the minimizer of(2.1)with g replaced by gδand{uδ,ξδ}be the solution of system(4.1)–(4.7)in which f=fδand g=gδ.In view of the uniqueness obtained in Section 5,the minimizer fδis unique as T is relatively small. Theorem 6.1 Assume f(x),fδ(x)be two minimizers of the optimal control problem(P)corresponding to g and gδ,respectively.Then Proof By taking τ=f when f=fδand taking τ=fδin(4.8),we get Setting therefore Uδand Ξδsatisfy By applying Lemma 2.2 we know that equation(5.2)only has zero solution and hence Furthermore,ξδverifies the following equation By virtue of(6.4)and(6.7),we obtain In view of(6.2),(6.3),(6.6),and(6.8)we get From the assumptions of Theorem 6.1 and owing to Lemma 5.1,we get This completes the proof of Theorem 6.1. Remark 6.2 We should point out that the uniqueness and stability of the optimal solution,obtained by using the optimal control method(OCM),effectively depend on the choice of the regularization parameter ν.Suppose that Then owing to Theorem 6.1 we get where f is the solution of problem(P),therefore the reconstructed optimal solution is unique and stable,this is consistent with the existing results(see,for instance,[18]).It is also worth noting that analogous results regarding the stability may also be obtained by applying the Tikhonov regularization method(TRM),see also[18].For more thorough discussion on the regularization parameter for ill-posed problems,we refer the readers to references[10,18,20]. Two experiments were performed with a natural soil and sand-clay with 20%of organic matters having different porosities,and polluted with heptane. For the first experiment,to see Table 1. Table 1 Parameters value for the first experiment with a soil moisture equals to about 11%and the pollutant initial concentration in the liquid phase equals to 6.35 Kg/m3. For the second experiment,to see Table 2. Table 2 Parameters value for the second experiment with a soil moisture equals to about 7%and the pollutant initial concentration in the liquid phase equals to 23 Kg/m3.For the numerical computing of the optimal control problem(P)we utilize the discretize-then-differentiate approach,see for instance[4].In this approach we discretize the state equations,here we use the implicit Euler scheme in time and centered finite differences discretization in space.Moreover,we use composite trapezoidal rule for the integral term.Finally,we discretize the objective functional J by using the midpoint rule in order to derive the discrete adjoint equation and the discrete gradient of the discrete objective functional.In doing so,we consider the following problem slightly modified from(P) Table 3 Parameters value We define the function f as follows: In this case,the exact solution is Figure 1 illustrates this exact solution in(0,1)×(0,1): Figure 1 The exact solution We present in the following figure 2 the comparison between the exact and approximate solutions of the direct problem(P)at T=1min for M=50 and N=100 with L2-error equals to 1.1×10−3. Figure 2 The exact and numerical solutions at T=1min We use a descent method with line search to compute the control parameter f.This algorithm of resolution is described below. Algorithm 7.1 Given xfthe final space,T the final time,M the number of subintervals along x axis,N the number of subintervals along t axis,an initial vector F0∈RMand a tolerance ǫ. Step 1 Determine the state vector by[U]=direct(M,N,xf,T); Step 2 Determine the adjoint vector by[P]=adjoint(M,N,xf,T,U); Step 3 Calculate the gradient∇J; Step 4 Use a descent method with line search until convergence. We propose to compare three updating formulas for approaching the inverse of the Hessian matrix,including BFGS,DFP and SR1 formulas(see for instance[21]),to minimize the discretized cost functional J(F,U).The obtained results are listed in Table 4 where we take T=0.005min,M=100,N=200,ν =1×10−002and initial guess F0=6.22∗ones(M −1,1).The stopping criterion was er1<1.4901×10−006with er1is the relative change in x for SR1 method,on the other hand the stopping criteria was the maximal iteration for getting the best point for BFGS and DFP methods.We can see that the SR1 updating formula with trust region(see also[21])gives best results in comparison with the others updating formulas,namely,BFGS and DFP formulas. Table 4 Comparison for different updating formulas The inverse problem of identifying the coefficient in an integro-differential parabolic equation of a pollution problem arising in porous media,has an important application in engineering sciences and many industrial fields.In this paper,on the basis of the optimal control framework,we treat the inverse problem(P)consisting in determining the initial pollutant concentration in the liquid phase since we can compute its gaseous concentration from final measurement.The existence,uniqueness and stability of the minimizer for the cost functional are established.Some numerical results are presented for minimizing the cost functional by applying the Quasi-Newton type methods.This paper focuses on the theoretical analysis of the one-dimensional parabolic integro-differential inverse problem.However,the obtained numerical results in this paper are satisfactory.For two-dimensional case,the method proposed in this paper is also applicable.We notice that the two-dimensional case may be more interesting in engineering and applied sciences.The numerical computations of the two-dimensional case will be taken into consideration in the next work.2 Optimal Control Problem
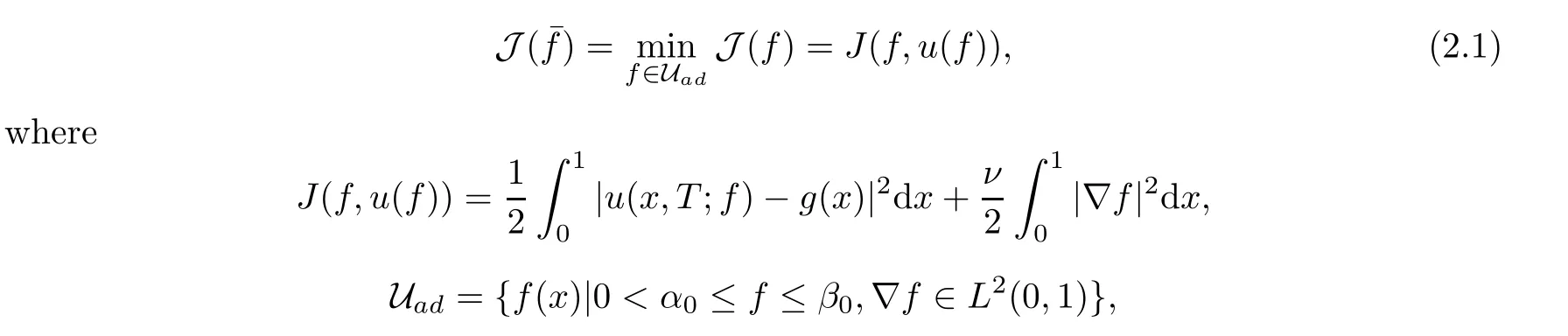

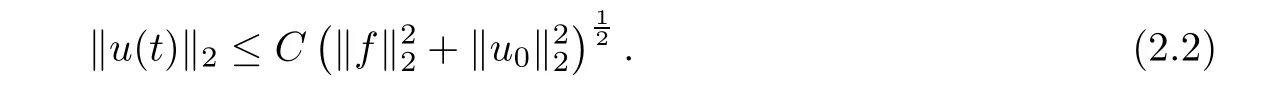
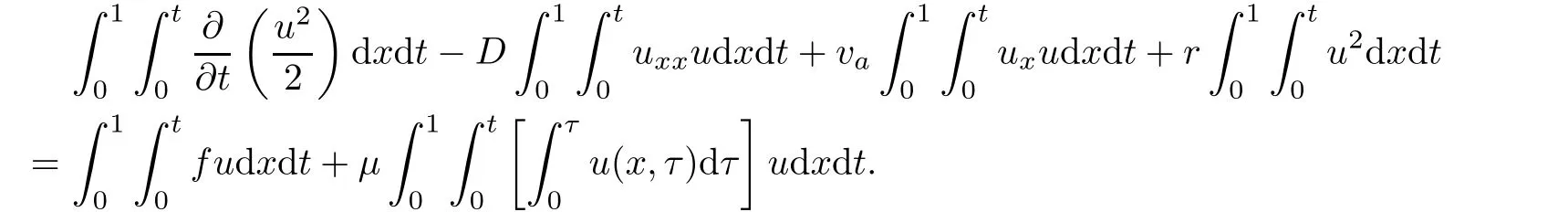

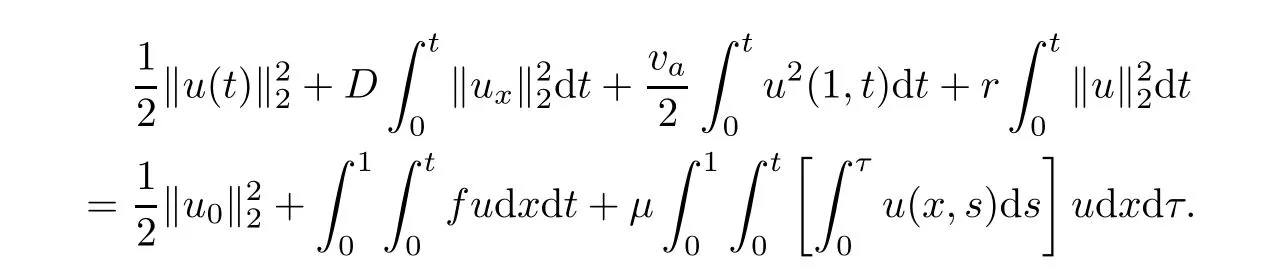
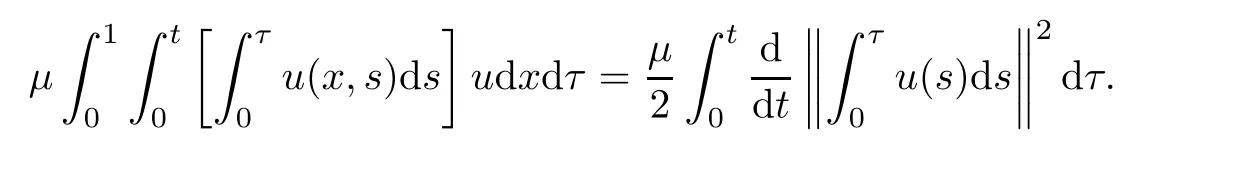

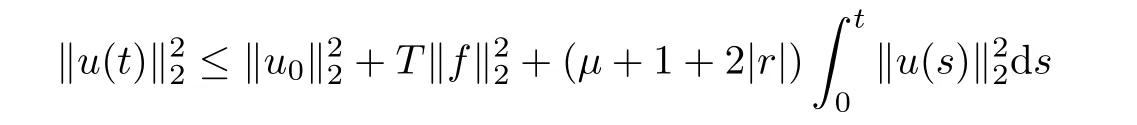
3 Existence of Minimizer for Cost Functional

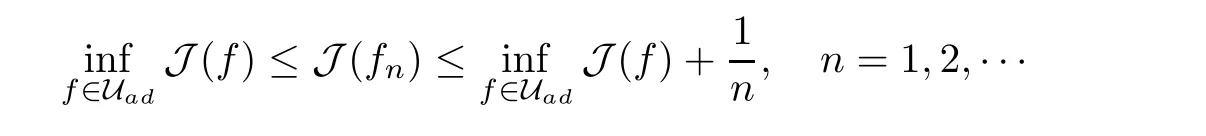

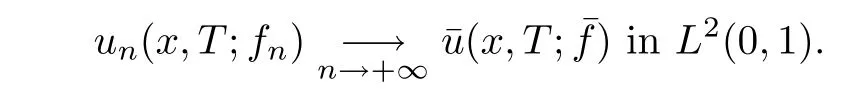
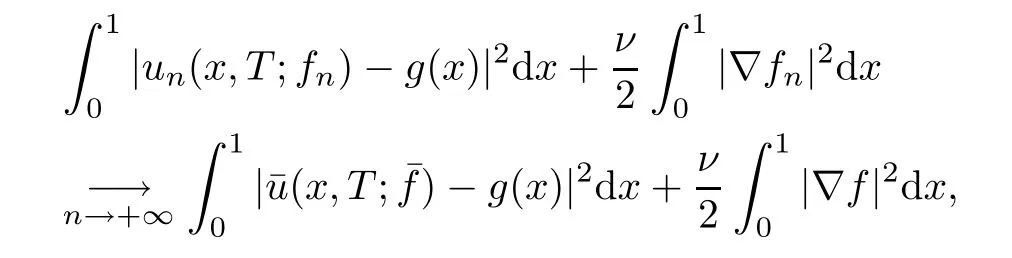
4 Necessary Condition
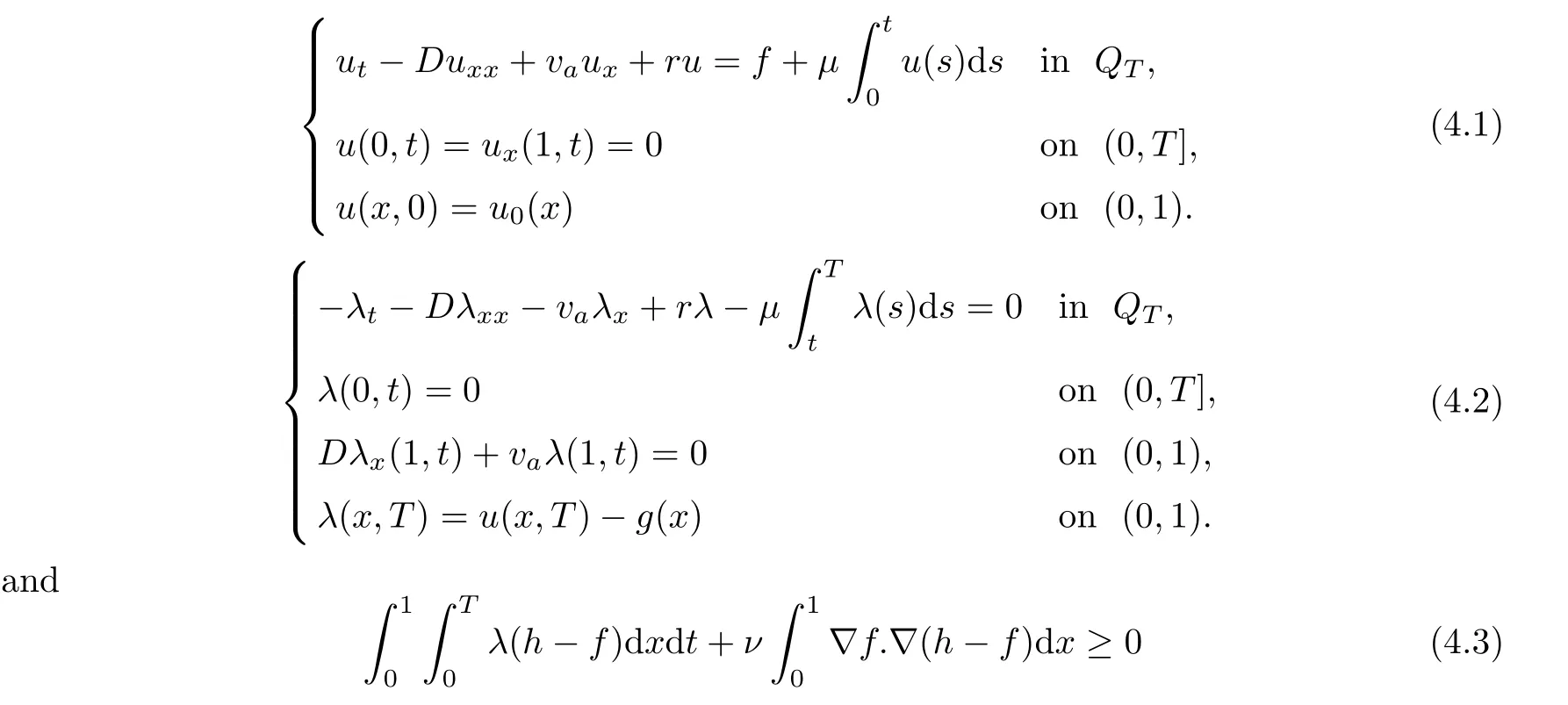


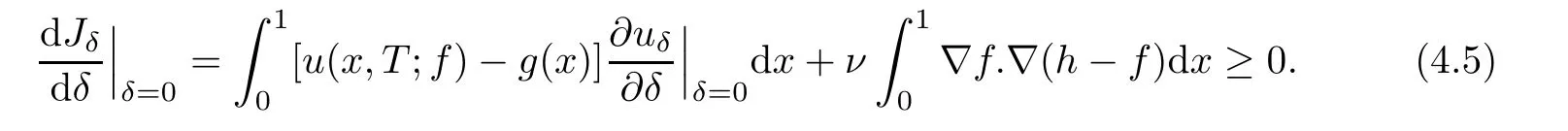
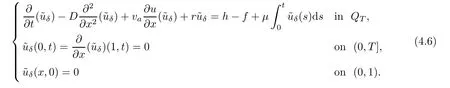



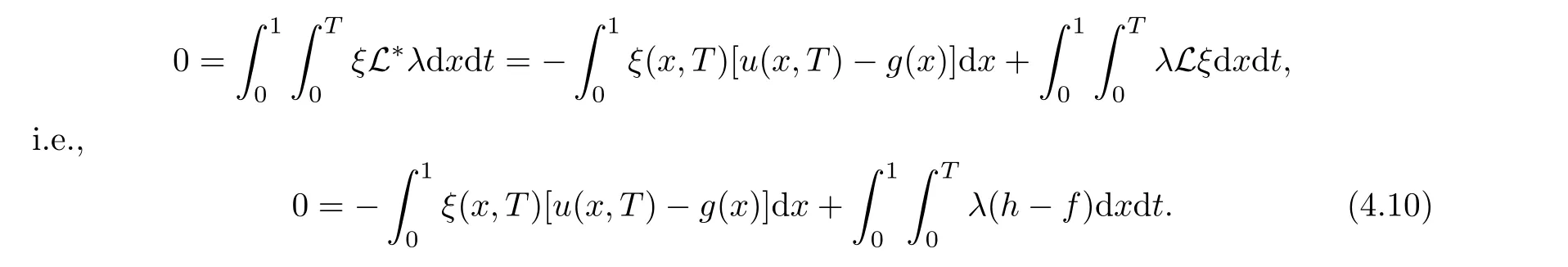
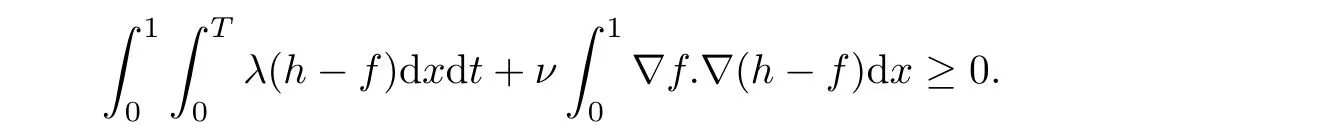
5 Uniqueness Result
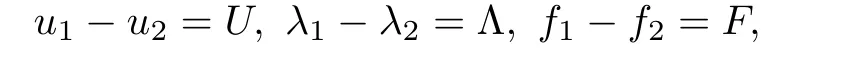
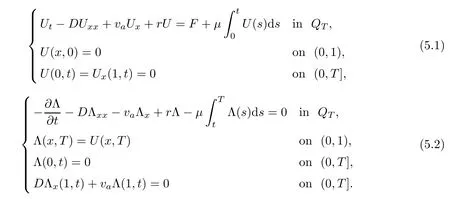
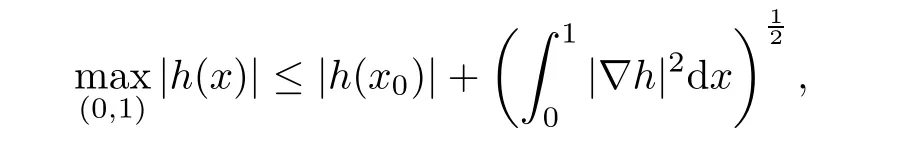

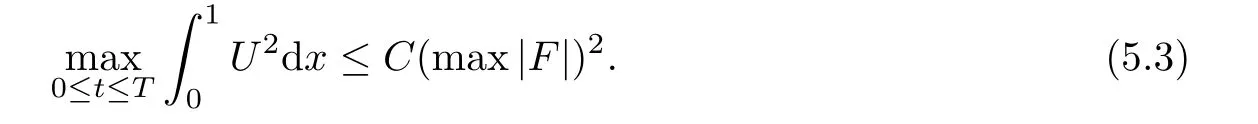



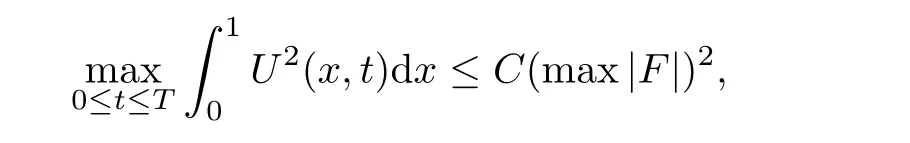


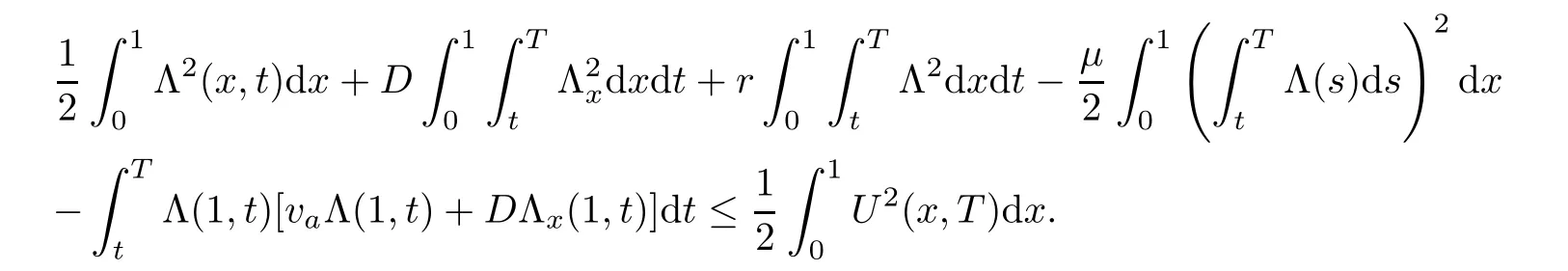
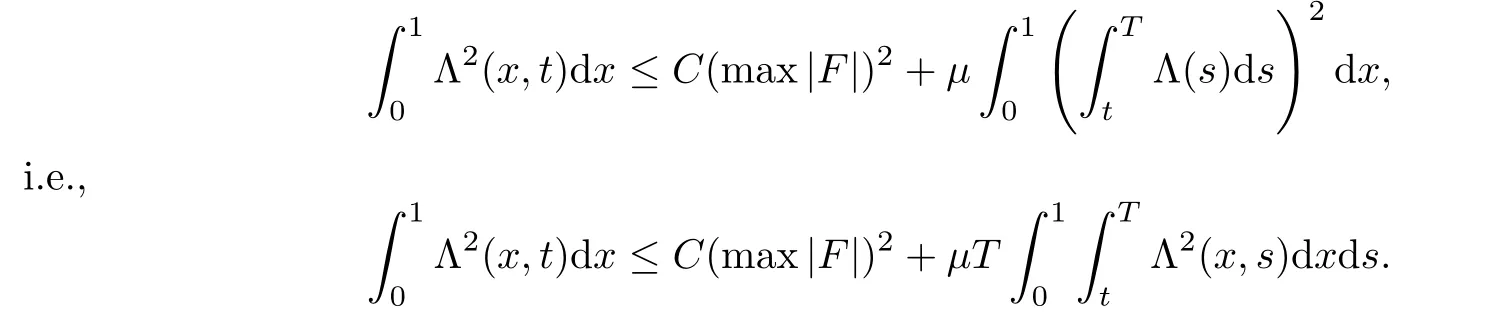







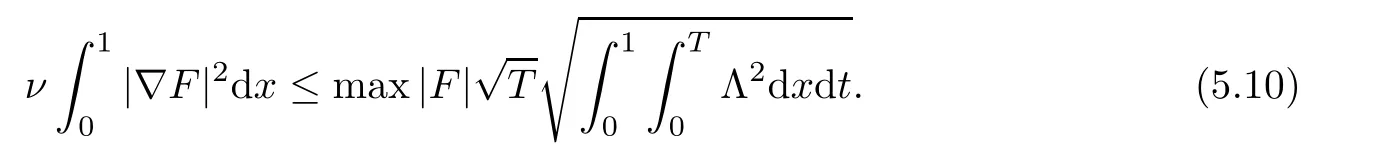





6 Stability

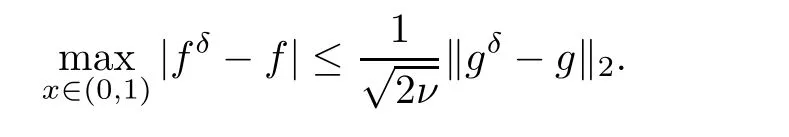
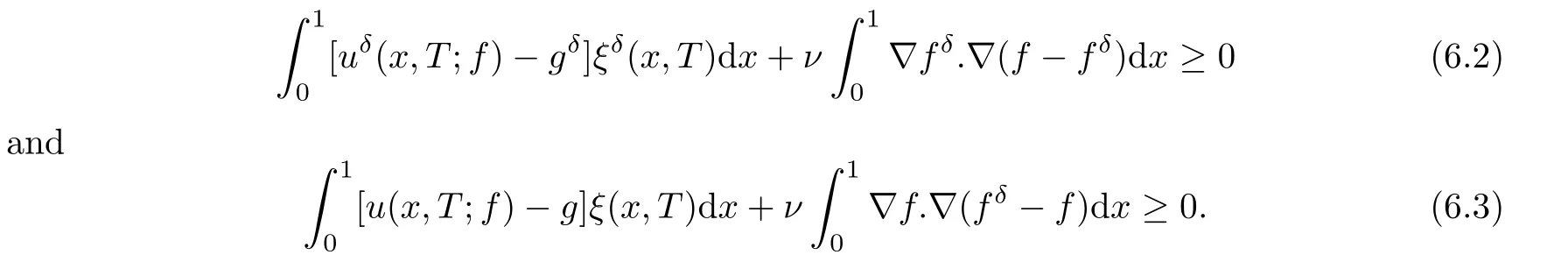
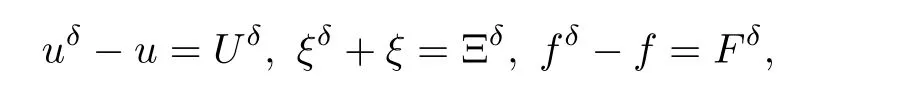




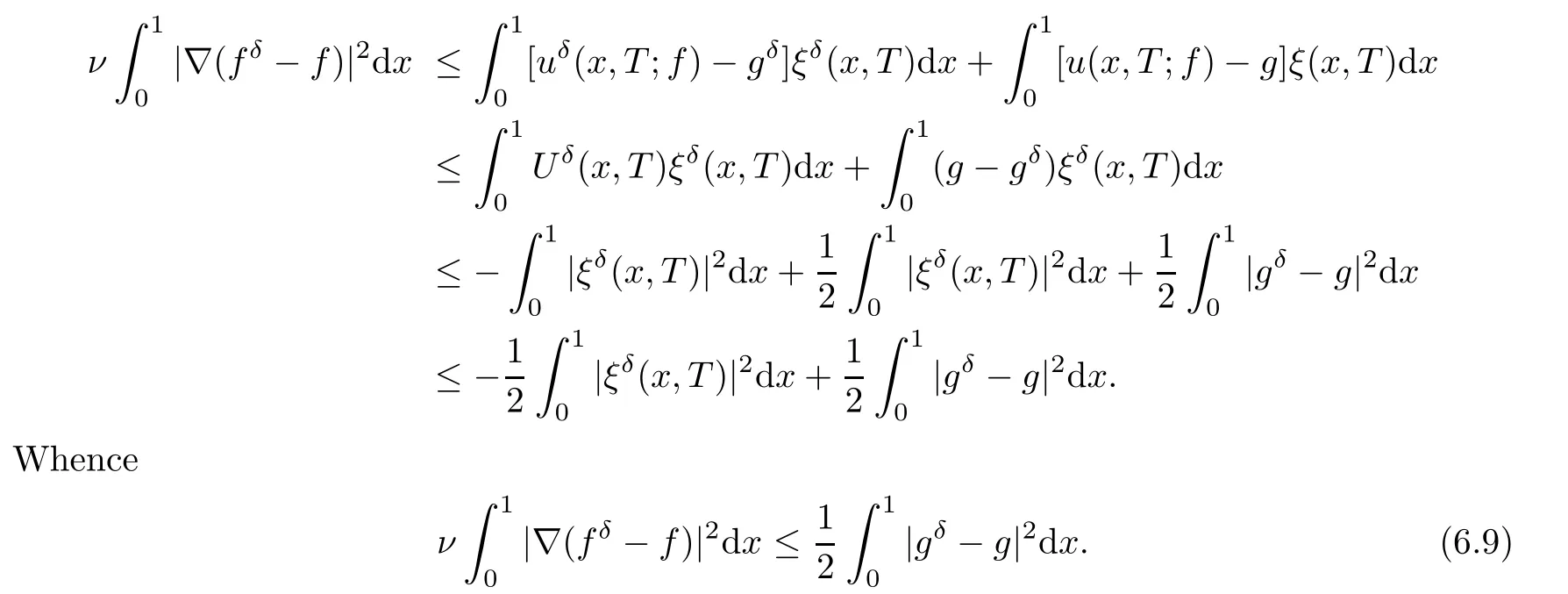

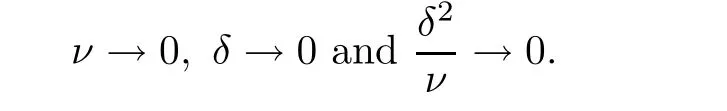
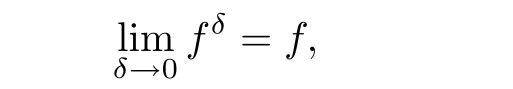
7 Numerical Results


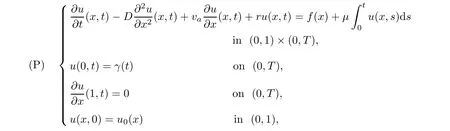

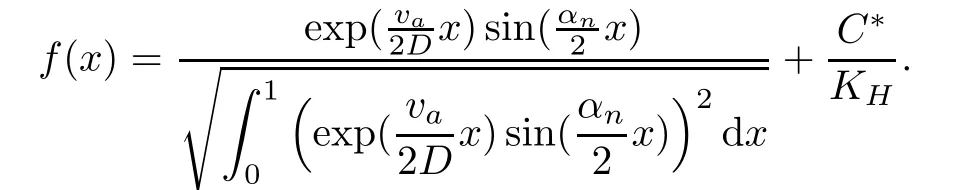


8 Concluding Remarks
 Acta Mathematica Scientia(English Series)2018年4期
Acta Mathematica Scientia(English Series)2018年4期
