OPTIMIZATION APPROACH FOR THE MONGE-AMP`ERE EQUATION∗

Fethi BEN BELGACEM

Department of Mathematics,Laboratoire EDP(LR03ES04),Faculty of Sciences of Tunis,1060 Tunis,Tunisia

E-mail:fethi.benbelgacem@fst.rnu.tn;fethi.benbelgacem@isimm.rnu.tn

Abstract In this paper,we introduce and study a method for the numerical solution of the elliptic Monge-Ampère equation with Dirichlet boundary conditions.We formulate the Monge-Ampère equation as an optimization problem.The latter involves a Poisson Problem which is solved by the finite element Galerkin method and the minimum is computed by the conjugate gradient algorithm.We also present some numerical experiments.

Key words elliptic Monge-Ampère equation;gradient conjugate method; finite element Galerkin method

1 Introduction

In this paper,we present a numerical solution for the following Monge-Ampère problem

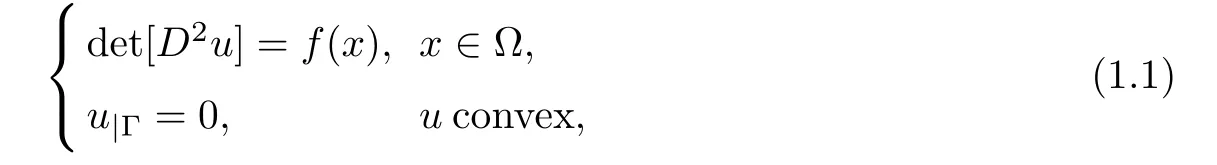
where Ω is a smooth convex and bounded domain in R2,?D2u?is the Hessian of u and f∈C∞(Ω),f>0.

Equation(1.1)belongs to the class of fully nonlinear elliptic equation.The mathematical analysis of real Monge-Ampère and related equations was a source of intense investigations in the last decades;let us mention the following references(among many others along with[7,9,15]):[2,8,10–14],[17,chapter 4],[28].Applications to mechanics and physics can be found in[4,5,18,24,26,31],(see also the references therein).

The numerical solution of the Monge-Ampère equation as well as the related equations recently were reported in the literature.Let us mention references[4,11,25,26,28,29,32,33,39];the method discussed in[11,25,32]is very geometrical in nature.In contrast with the method introduced by Dean and Glowinski in[19–21],which is of the variational type.

On the existence of a smooth solution for(1.1),we recall that if f∈C∞(Ω)equation(1.1)has a unique strictly convex solution u∈C∞(Ω)(see[14]).

To obtain a numerical solution for(1.1),we propose a least-squares formulation of(1.1).For that purpose,we formulate the Dirichlet Monge-Ampère problem as a well defined optimization problem,to which we associate a well defined functional whose minimum provides us with the solution to the Monge-Ampère problem after resolving the Poisson one by the finite element Galerkin method.The minimum is computed by the conjugate gradient method.

The rest of this article is organized as follows.In Section 2,we introduce the optimization problem.The different steps of the method are discussed in Section 3.In Section 4,we will expose some numerical results.Conclusions are made in Section 5.

2 Formulation of the Dirichlet Problem for the Elliptic Monge-Ampère Equation

Let uIbe the solution of(1.1).Let λ1and λ2be the eigenvalues of the given matrix[D2uI].We have

Then λ1and λ2are the solutions of the following equation

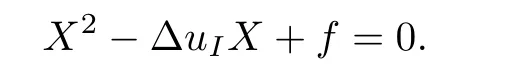
So

Then

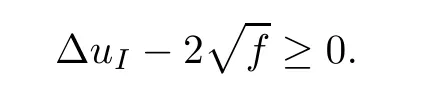
Let us set

We conclude that uIis a solution of the following Dirichlet Poisson problem

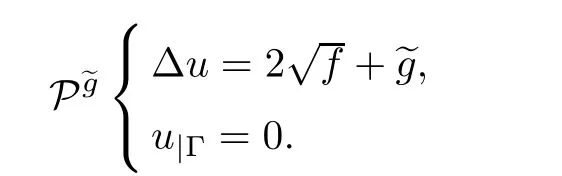
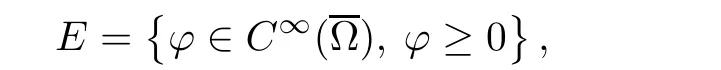
as follows

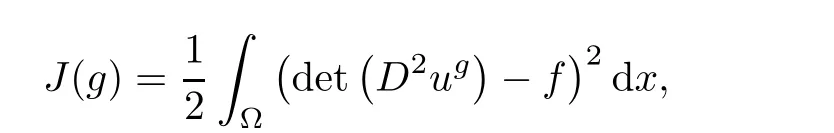
where ugis the solution of the Dirichlet Poisson problem

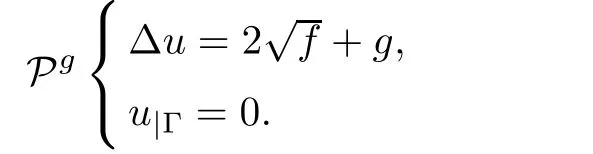
The minimization problem

is thus a least-squares formulation of(1.1).

Theorem 2.1 uIis the strictly convex solution of(1.1)if and only if there exists a unique solutionof(2.1)such that uI=

ProofSince uIis a solution of(),we have uI=.So J=0 andis a unique solution of(2.1).

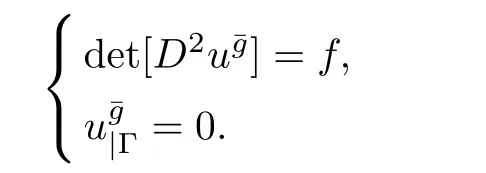
3 Numerical Method

3.1 Description of the Algorithm

The algorithm we consider to solve problem(2.1)which is based on the PRP(Polak-Ribiè-Polyak[36,37])conjugate gradient method reads.

Given g0∈E;loop over k∈N.

•The resolution of the Poisson problem?Pgk?:for k≥0,gkbeing known in E,solve

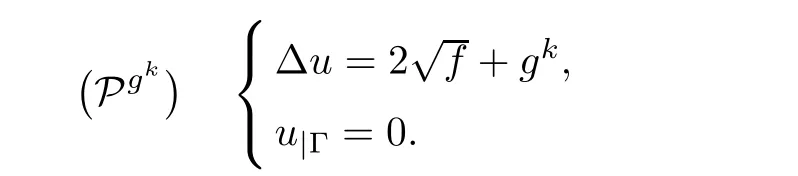
• Conjugate gradient method:computation of,and αk.

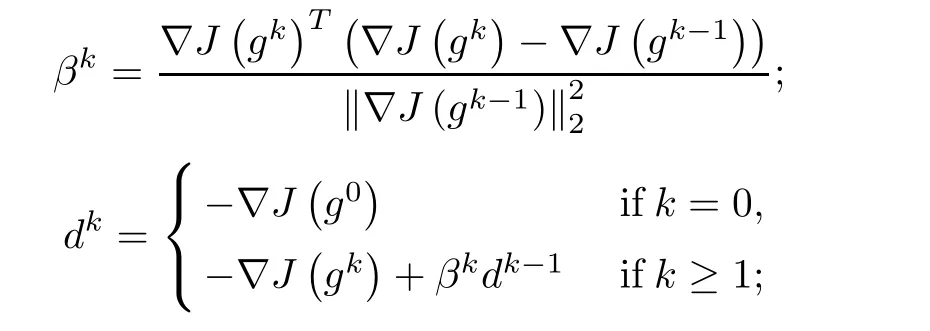
αkis determinited by Armijo line search.

•Update gk:

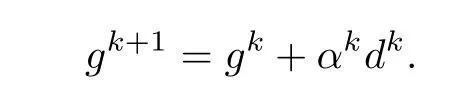
3.2 Solution of Sub-Problem(Pg)

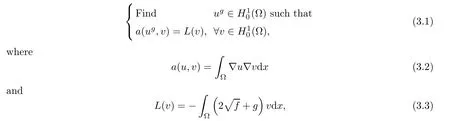
We consider first the variational formulation of(Pg)a in(3.2)is coercive on(Ω).For f ∈ L2(Ω),we have∈ L2(Ω).Since Ω is bounded and for g∈ L2(Ω),L in(3.3)is continuous,then by the Lax-Milgram theorem(Pg)has a unique solution ug.

3.3 Finite Element Approximation of the Minimization Problem

To make it simpler,we assume that Ω is a bounded polygonal domain of R2.Let Thbe a finite triangulation of Ω(like those discussed in e.g,[16]).

We introduce as finite dimensional spaces

with P1as the space of the two-variable polynomials of degree ≤ 1.A function ϕ being given in H2(Ω),we denoteby D2

ij(ϕ).It follows from Green’s formula that

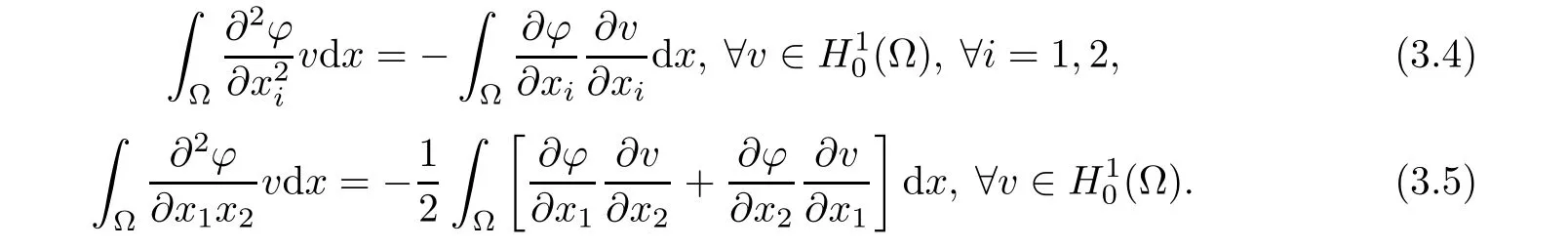
Let ϕ∈Vh;taking into consideration relations(3.4)and(3.5),we define the discrete analogues of the differential operatorsby

To compute the above discrete second order partial derivatives,we will use the trapezoidal rule to evaluate the integrals on the left hand sides of(3.6)and(3.7).We consider the setof the vertices of ThandWe define the integers Nhand N0hbySo dimVh=Nhand dimV0h=N0h.

It is well known(e.g.,[16])that the setsare vector bases of Vhand V0h,respectively.

We denote by Akthe area of the polygonal which is the union of those triangles of Thwhich have Pkas a common vertex.By applying the trapezoidal rule to the integrals on the left hand side of relations(3.6)and(3.7)we obtain

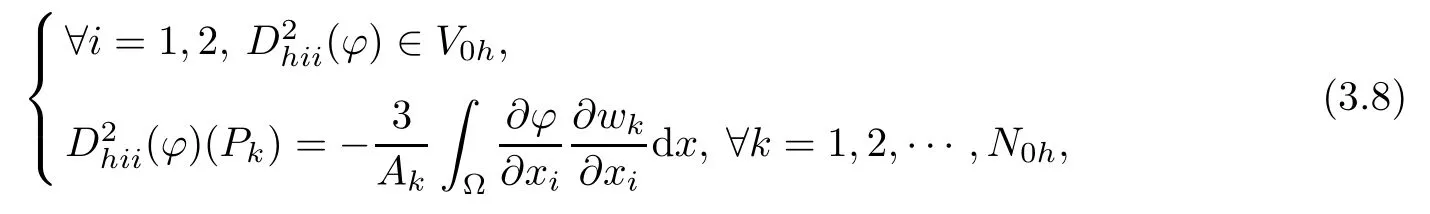
Computing the integrals on the right hand sides of(3.8)and(3.9)is quite simple since the first order derivatives of ϕ and wkare piecewise co nstant.

Taking the above relations into account,we approximate the space E by

and then the minimization problem(2.1)by

where

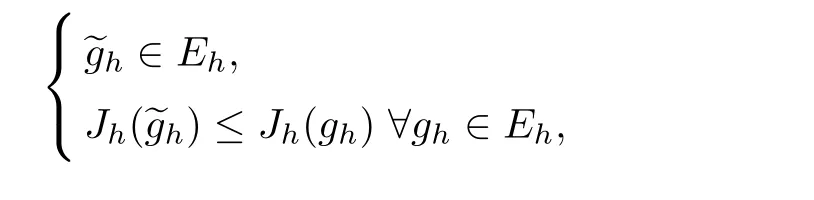
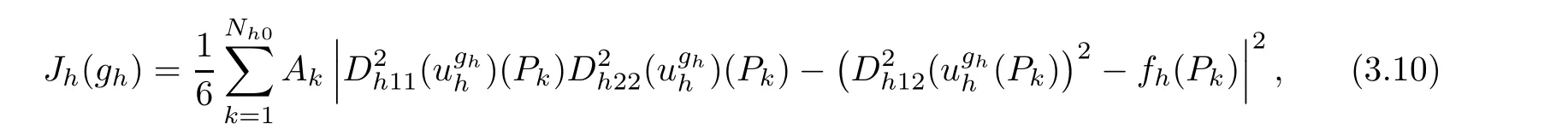
Remark 3.1 There are many approches for finding an available step size αkh.Among them the exact line search is an ideal one,but it is cost-consuming or even impossible to use to find the step size.Some inexact line searches are sometimes useful and effective in practical computations,such as Armijo line search[1],Goldstein line search and Wolfe line search[24,38].

The Armijo line search is commonly used and easy to implement in practical computations.

By the Lax-milgram theorem,we can easily show that(3.11)has a unique solution

Remark 3.2 It is clear from(3.10)that to compute∇Jh(gh),we need···,Nh.Since gh∈ Vh,we haveBy deriving the Poisson equation in Pgwith repect to gm,one can easily see thatcan be obtained by resolving a Poisson problem with wmon the right hand side.

4 Numerical Experiments

In this section,we are going to apply the discussed method in the previous section to the solution of some test problems.For all these test problems,we shall assume that Ω is the unit disk.We first approximate Ω by a polygonal domain Ωh.We consider Thas a finite triangulation of Ωh.

Remark 4.1 When computing the approximate solutions of these problems,we stopped the iterations of the algorithm as soon as|∇h(gh)|≤ 10−6.

The first test problem is expressed as follows

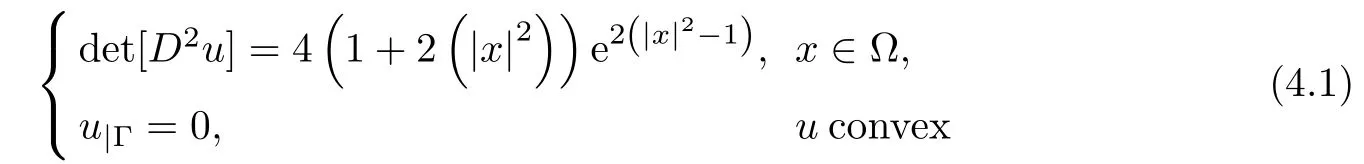
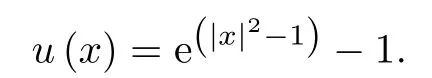
We have discretized the optimization problem associated to problem(4.1).We solved the Poisson problem encountred at each iteration of the algorithm by fast Poisson solvers.

We use three different constant values as an initial guess forThe results obtain after 68 iterations are summarized in Table 1(wheredenotes the computed approximate solution and k.k0,Ω=k.kL2(Ω)).

To see the effect of the initial g0on the calculations,the functional J is plotted against the step α for three differents values of g0.The graph of uobtained for h=1/128 is visualized on Fig.1.

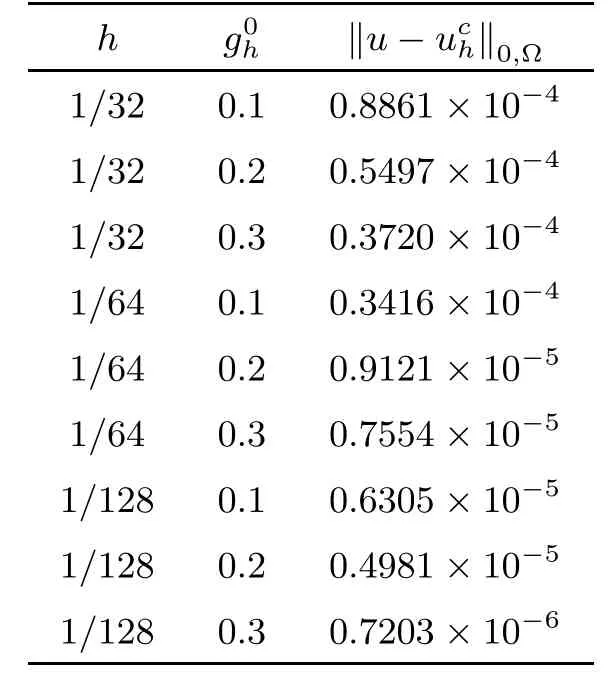
Table 1 First test problem:convergence of the approximate solution

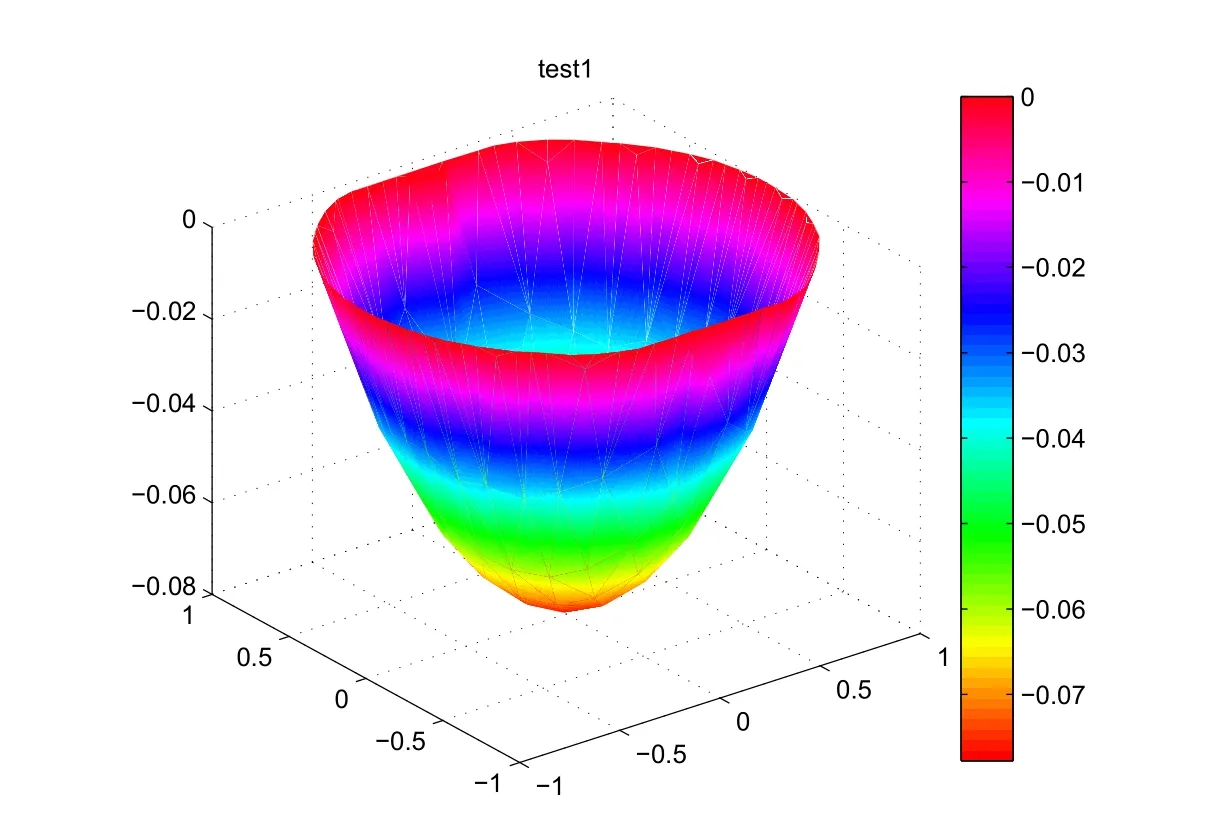
Fig.1 First test problem:surface plot of the computed solution

Remark 4.2 We did not try to find the optimal value of g0(it seems that it is a difficult problem).

We conclude from the results in Table 1 that the value g0=0.3 is optimal and quite accurate approximations of the exact solutions are obtained.This is confirmed by Fig.2.

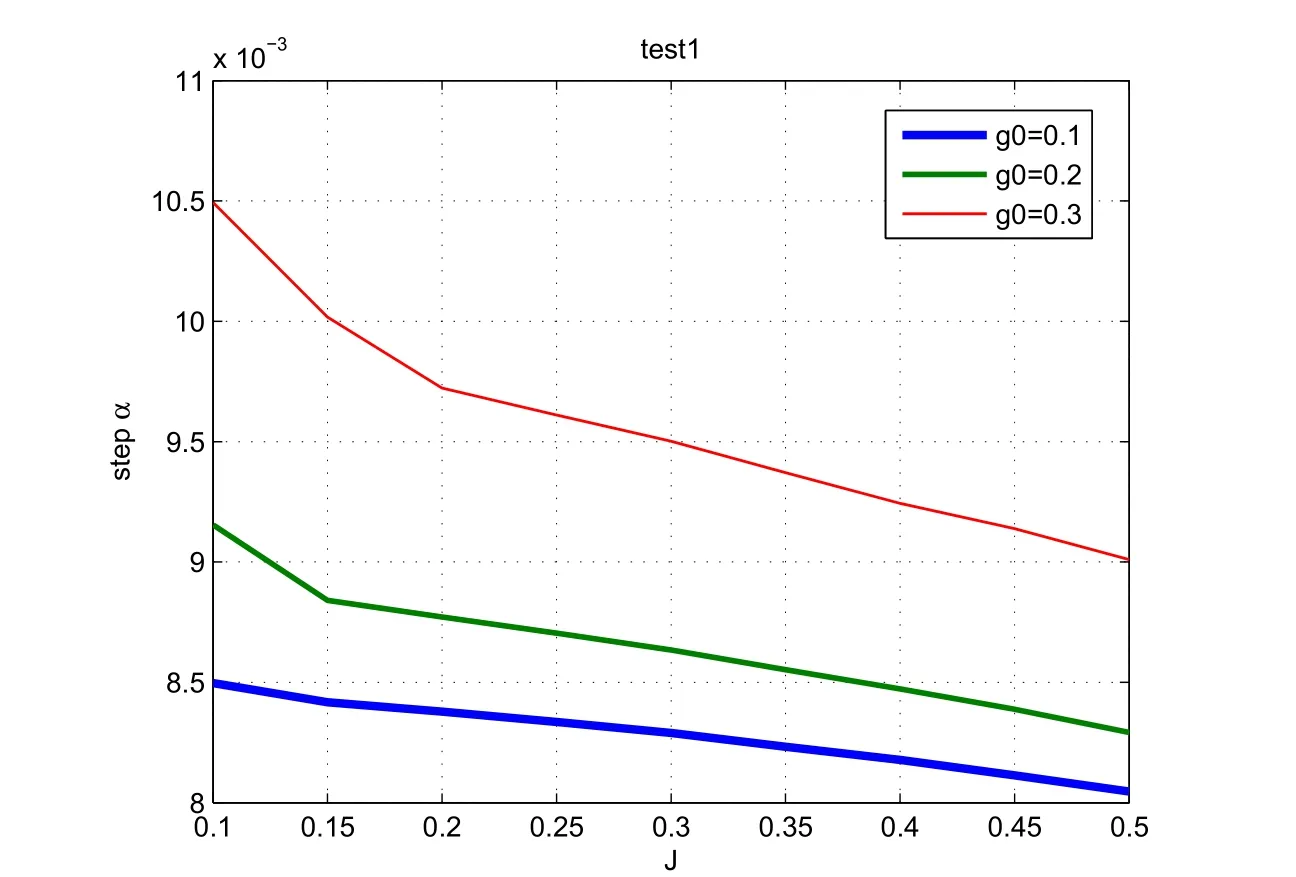
Fig.2 First test problem:The functional J against the step α for different values of g0

In the second test problem we take

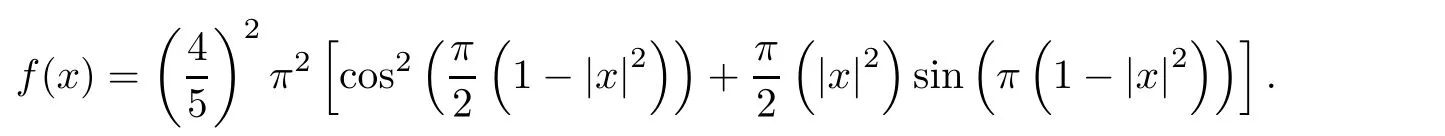
The solution to the corresponding Monge-Ampère problem is the function u∈C∞( Ω)defined by

The method provides after 64 iterations the results summurized in Table 2.

The value g0=0.3 is again optimal.

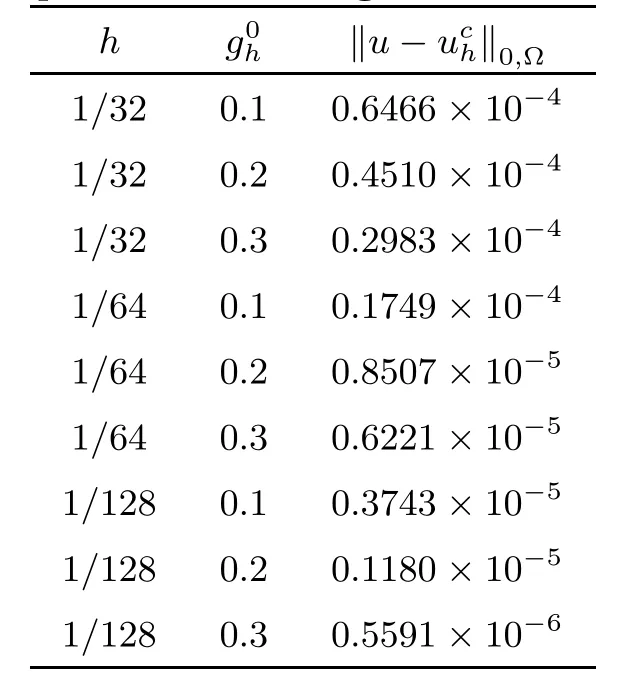
Table 2 Second test problem:convergence of the approximate solution

Fig.3 Second test problem:surface plot of the computed solution

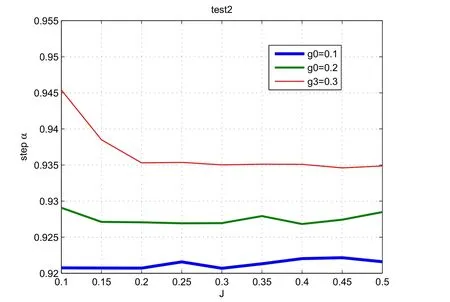
Fig.4 Second test problem:the functional J against the step α for different values of g0

The comparaison of the results in the above table with those of Table 1 and Table 2 shows that this method provides a more accurate solution in the first test and the second one.One can put the blame on the fact that we have used a line search that guarantees the global convergence of the PRP method and the initial guess is not optimal in this case.

The third test problem is defined as follows

The function u given by

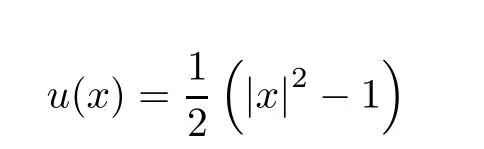
is the solution of(4.2)and u∈C∞( Ω).

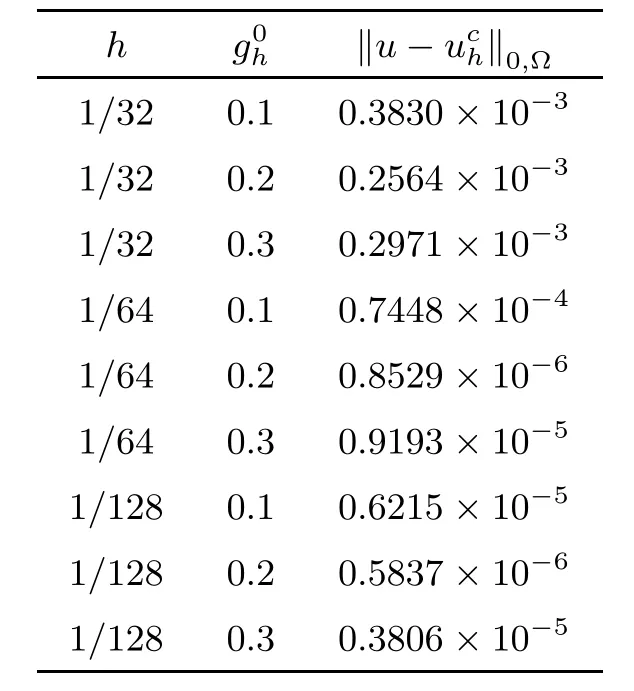
Table 3 Third test problem:convergence of the approximate solution

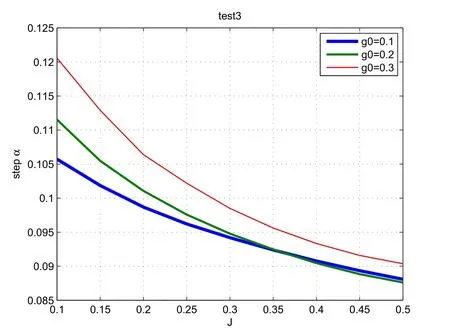
Fig.6 Third test problem:the functional J against the step α for different values of g0

We deduce from Table 3 that g0=0.2 is an optimal value.

Unfortunately,we did not find any other initial value that gives more accurate results.Even for g0=0.4,the results are not satisfying.

5 Conclusions

We have presented a new numerical method for the Dirichlet Monge-Ampere equation by introducing an equivalent optimization problem involving a Poisson Dirichlet problem.This latter is resolved by a finite element method and the minimum is computed by a conjugate gradient method.The results presented here are satisfactory and can be improved if one finds the optimal initial data.An attractive feature of our method is its simplicity:since it is based on a Poisson solver.This method raises some open questions.Hereafter,we list two questions.How can we study the regularity of the Monge-Ampere equation by considering the optimization problem introduced here?What is the suitable method to compute the optimal choice of the initial data?