THE REPRESENTATION OF THE SOLUTION OF STURM-LIOUVILLE EQUATION WITH DISCONTINUITY CONDITIONS∗
Ozge AKCAY
Department of Mathematics,Mersin University,Mersin 33343,Turkey
E-mail:ozge.akcy@gmail.com
Abstract The aim of this paper is to construct the integral representation of the solution of Sturm-Liouville equation with eigenparameter-dependent discontinuity conditions at an interior point of the finite interval.Moreover,we examine the properties of the kernel function of this integral representation and obtain the partial differential equation provided by this kernel function.
Key words Sturm-Liouville equation;discontinuity conditions;integral representation
1 Introduction
The boundary value problems for Sturm-Liouville equations with discontinuities inside the interval often appear in mathematical physics,geophysics,electromagnetic,elasticity and other branches of engineering and natural sciences.For example,we take a rod consisting of two homogeneous parts that have different modulus of elasticity with cross section and connected at the point x=a.The vibration problem of this rod can be expressed as follows
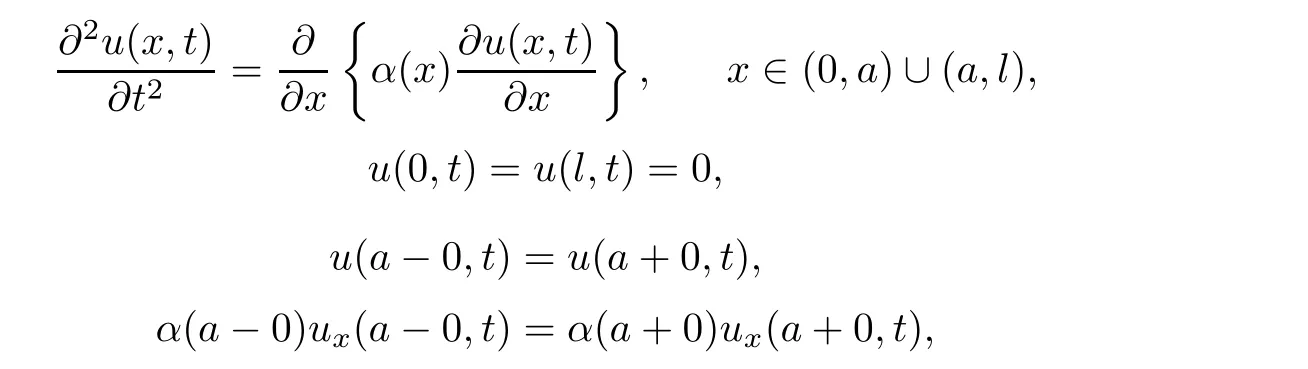
where l is the lenght of this rod,α(x)is the coefficient of elasticity of the rod and the piecewise continuous function

Moreover,the boundary value problems with discontinuities in an interior point arise in geophysical models for oscillations of the Earth[4,14],in heat and mass transfer problems[16]and in vibrating string problems which an interior point is under the action of a damping force[32],in addition,for the various applications of discontinuous boundary value problems,the works[10,13,31,35]can be given.
In this paper,we consider the Sturm-Liouville equation

with discontinuity conditions at the point

where q(x)is a real valued function in L2(0,π),α and β are positive real numbers,λ is a spectral parameter.It must be noted that for the eigenparameter-dependent discontinuity conditions(i.e.β 6=0),we can see the work of Gomilko and Pivovarchik[8],in this work,the problem of vibrations of a smooth inhomogeneous string damped at an interior point is examined and this problem is reduced to a spectral problem with discontinuity conditions that contain the λ eigenparameter.
In recent years,the Sturm-Liouville problems with discontinuity conditions(or transmission conditions)at interior points of the interval began to attract a great deal of attention because of the applications of these problems in physics,mechanics and engineering.Hereby,this type of problems were widely investigated by many authors,also the investigations were continued and developed in many directions.For example,some aspects of the direct spectral problems were studied in[5,6,12,22–24,26,27,29,30]and the references therein,moreover,the inverse spectral problems(according to Weyl function and/or spectral data and etc.)are examined in the works[2,3,9,11,21,25,33,34]where further references can be found.
In the present paper,as different from other studies,we construct the new integral representation of the solution e(x,λ)of equation(1.1)satisfying discontinuity conditions(1.2)and the initial conditions
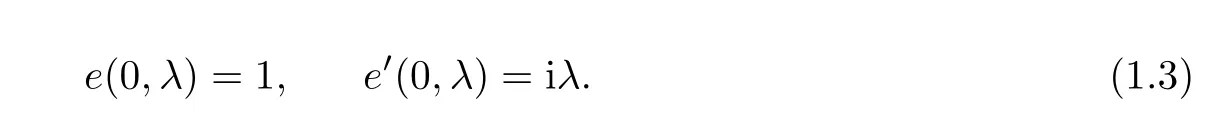
In the special cases of discontinuity conditions(1.2),the integral representation for the solution of equation(1.1)is obtained by Amirov[2]as β =0 and by Mammadova[19]as α =1.By the way,we note that the integral representations and transformation operators are used for the solution of inverse problems of spectral analysis(see[1,7,11,15,17,18,20,28]),especially,the relation between the potential function of the problem and the kernel function of the integral representation or transformation operator plays the central role in the solution of the inverse problems.Therefore,in this paper,we give this type of relation,examine the properties of the kernel function of constructed integral representation and obtain the partial differential equation provided by this kernel function.Additionally,unlike the other studies[9,19],it is shown that the kernel function is real valued and has a discontinuity along the line t=2a−x for x>a.
2 Main Results
In equation(1.1),assume that q(x) ≡ 0.Then,the solution e0(x,λ)of the equation−y′′= λ2y has the following form

Theorem 2.1 The solution e(x,λ)of equation(1.1)satisfying the discontinuity conditions(1.2)and initial conditions(1.3)can be expressed by the formula
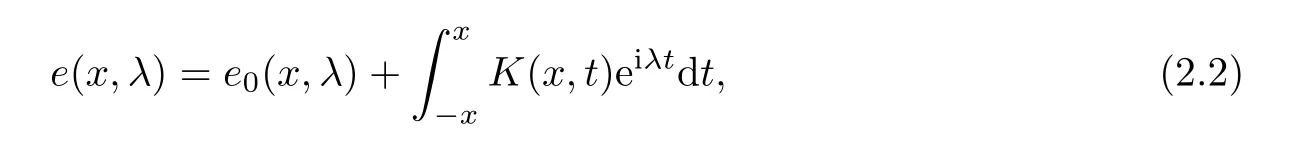
where the kernel K(x,.)∈ L1(−x,x)for each fixed x ∈ (0,a)∪(a,π)and satisfies the inequality
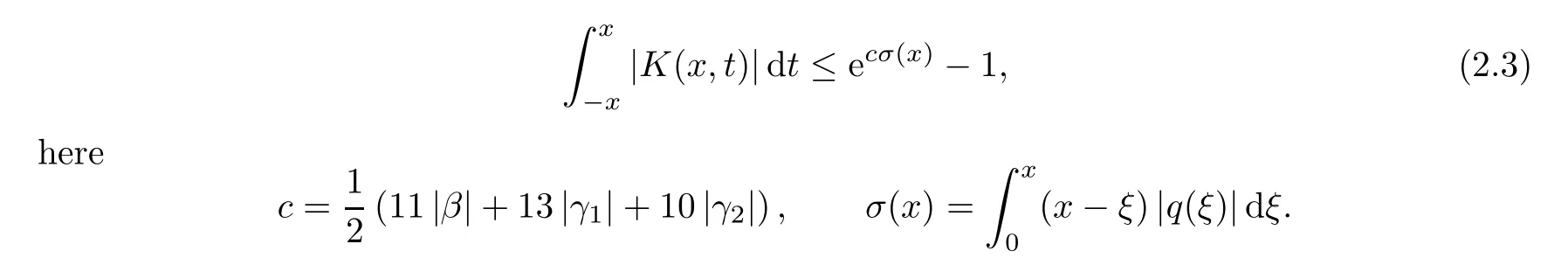
Moreover,the relations are valid,
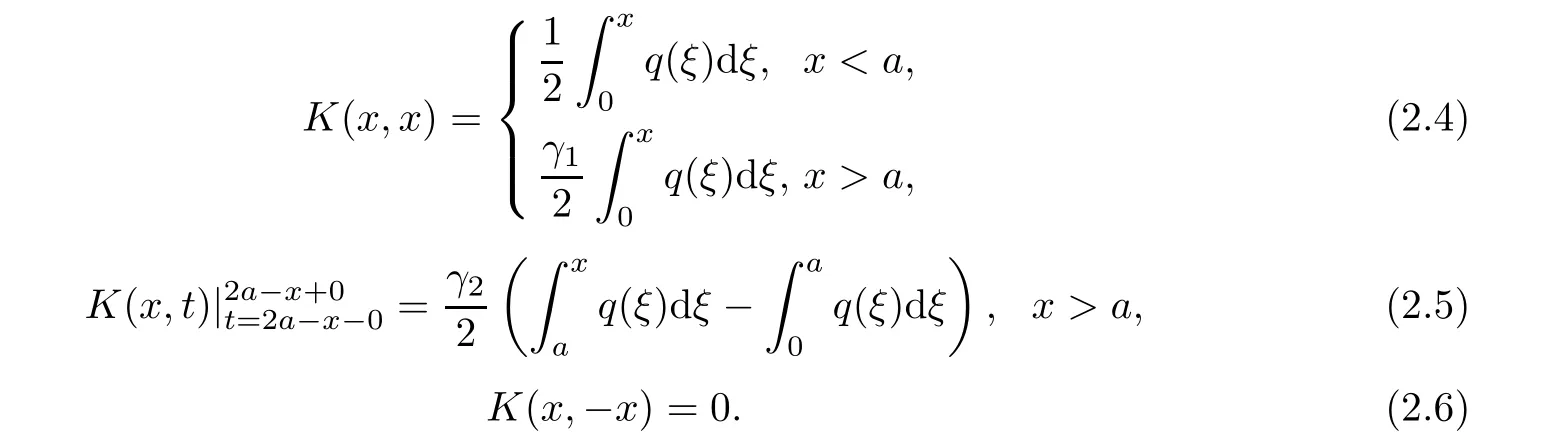
Proof In order to find the solution e(x,λ),the method of variation of constants can be applied.Consequently,the following equation is obtained

Equality(2.7)is an integral equation for the function e(x,λ).We seek the solution of this equation in form(2.2).It follows from(2.2)and(2.7)that
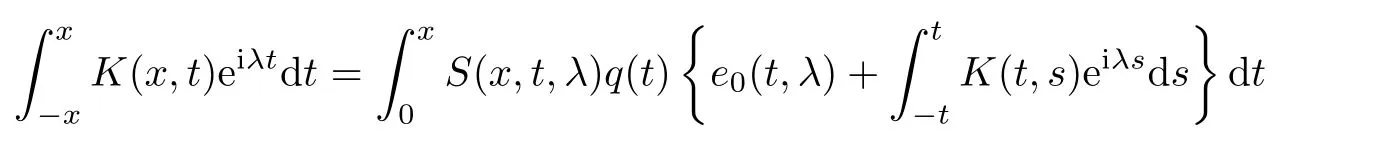
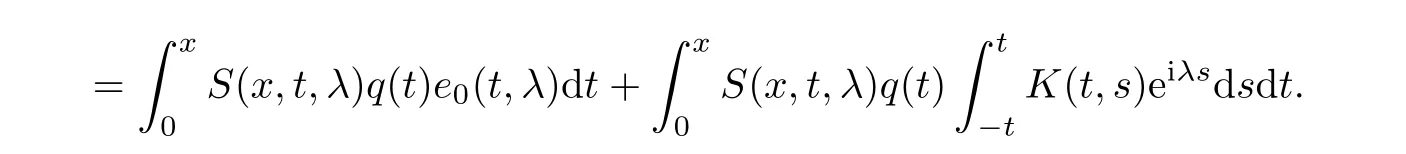
Thus,in order for such kind function to satisfy equation(2.7),it is necessary that
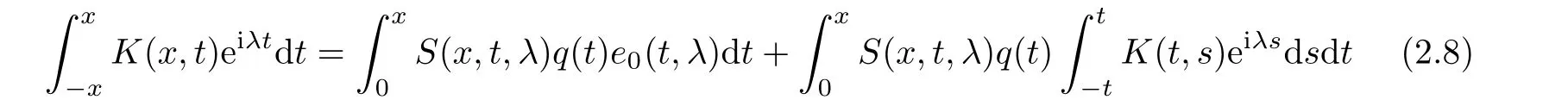
holds.Conversely,if K(x,t)satisfies this equality,then the function e(x,λ)satisfies equation(2.7).
Now,we express the right hand side of equality(2.8)as a Fourier transforms of some function.Consider the first summand from the right hand side of equality(2.8).In the case of x>a,we have
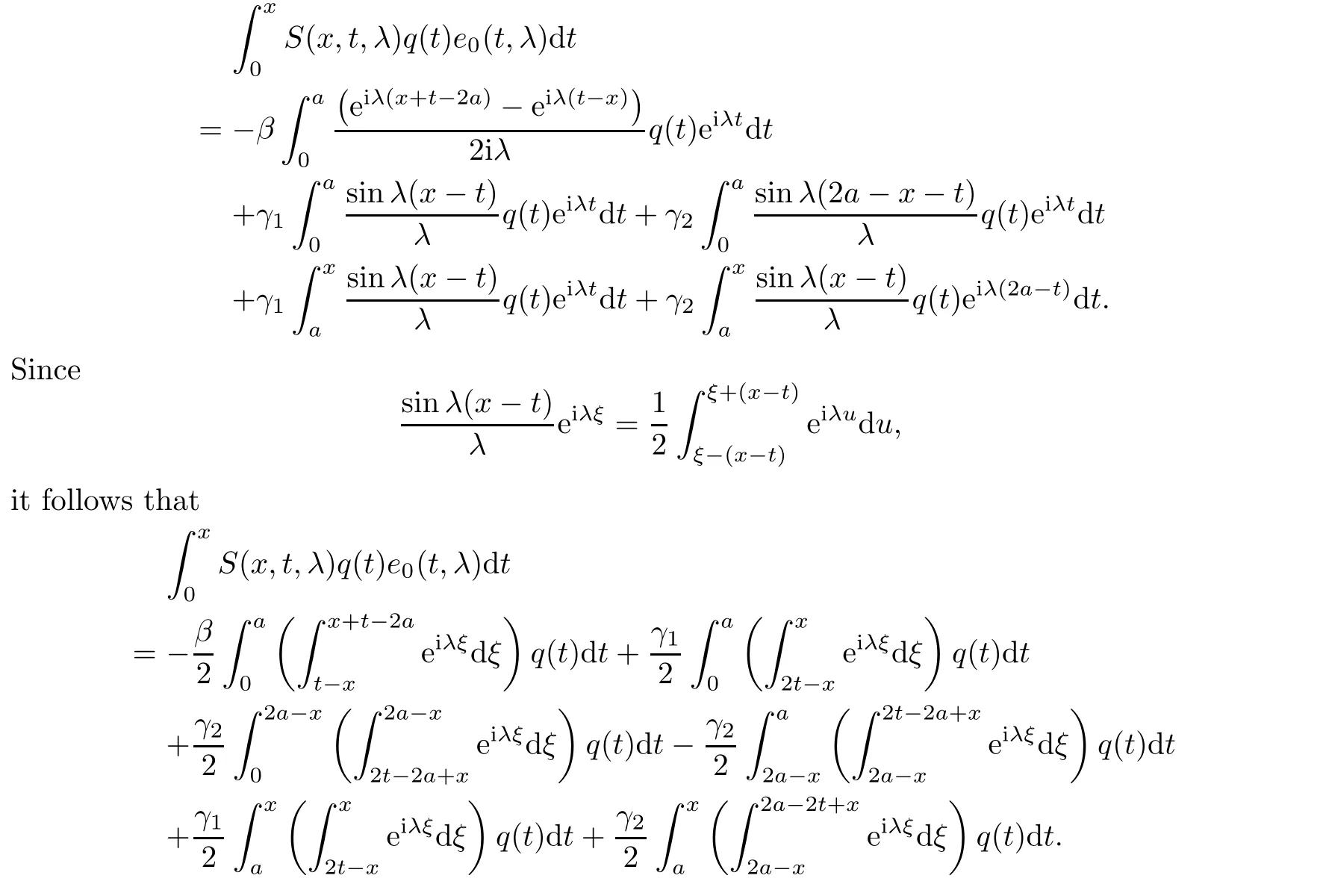
In this equality,changing respectively the integration order and denotation for integration variables,we find
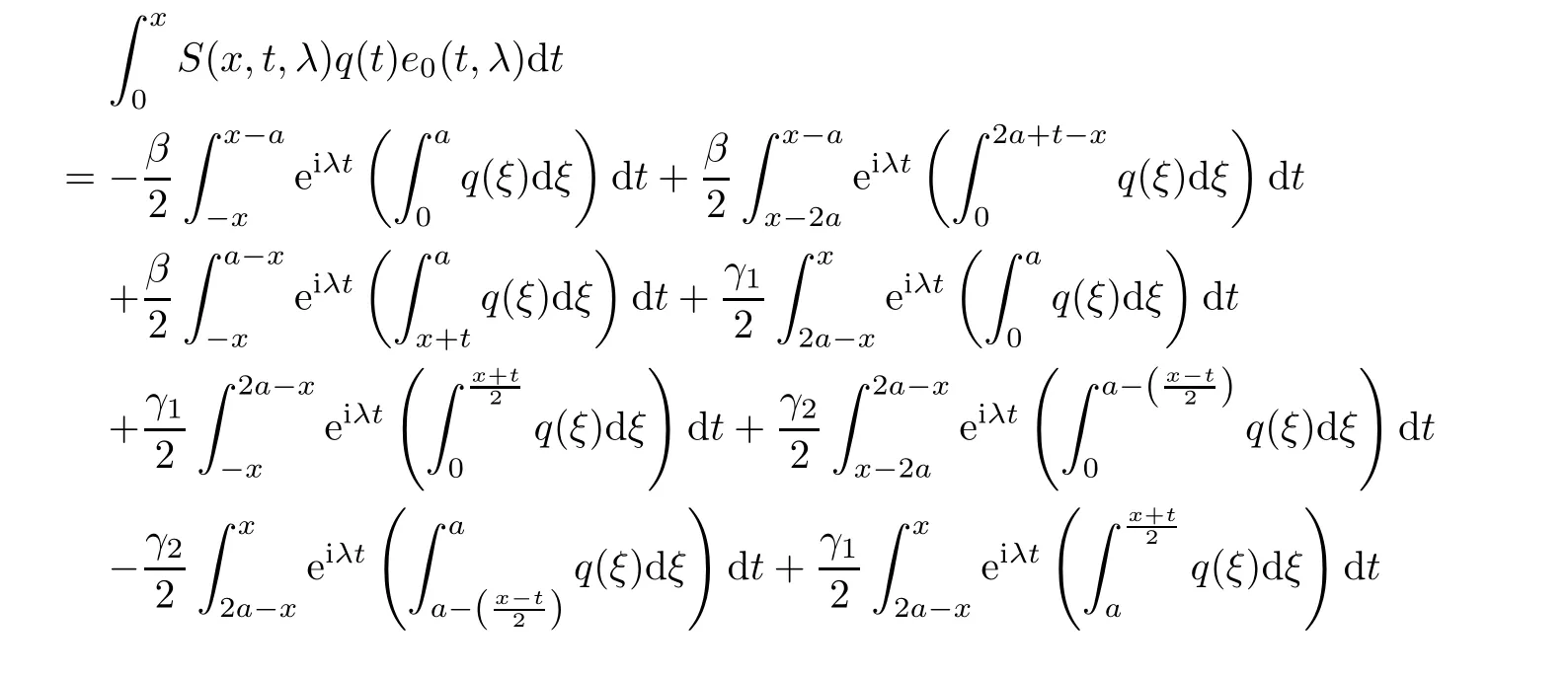
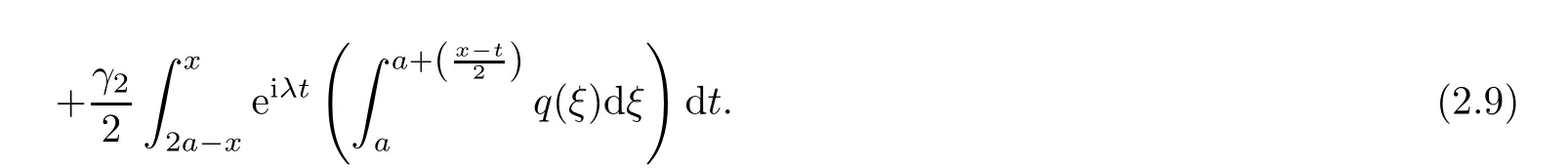
Now,take into account the second summand from the right hand side.In the case of x>a,we obtain

Extending the function K(t,s)by zero for|s|>|t|for any choice of t∈ (−x,x),we can write
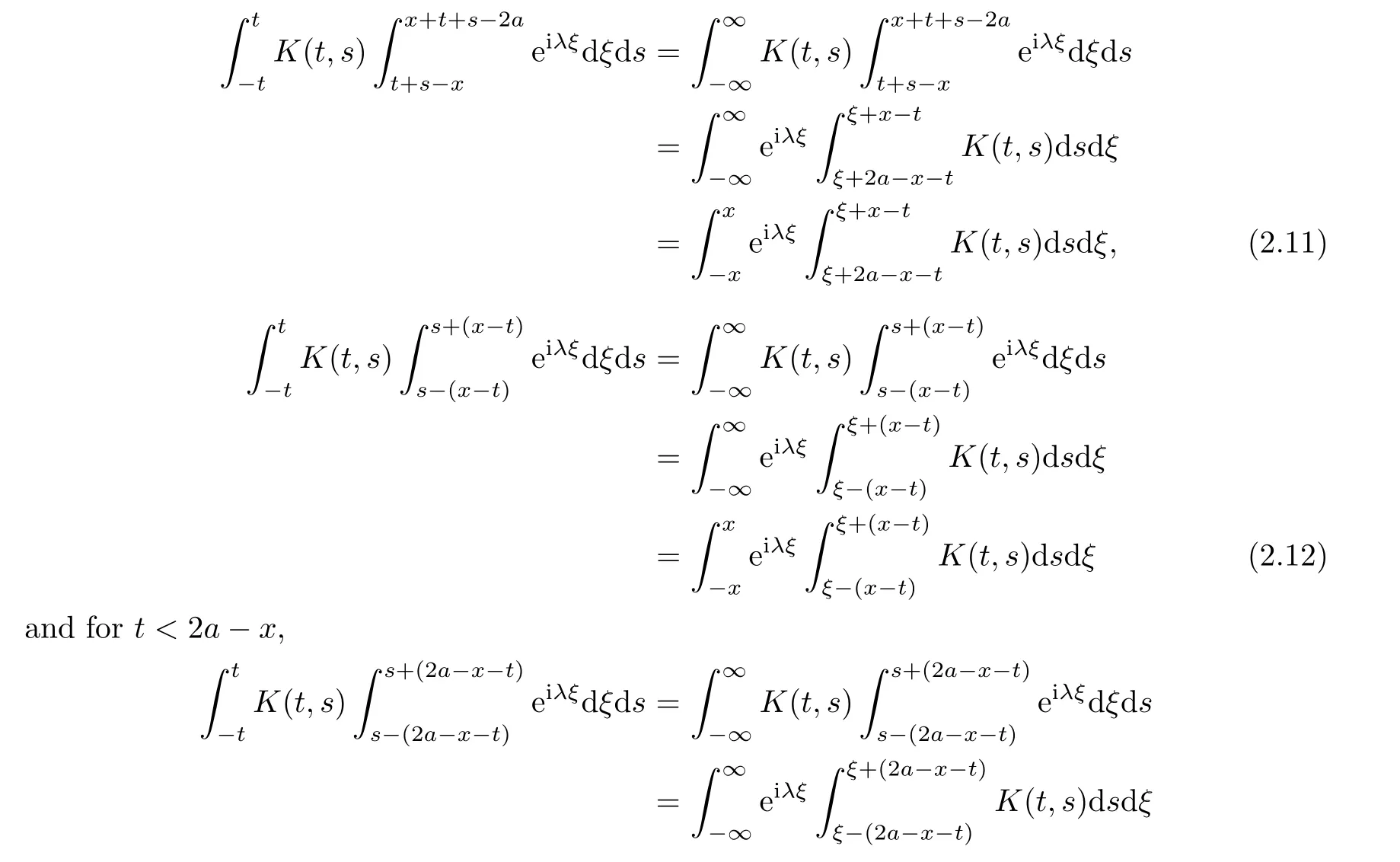
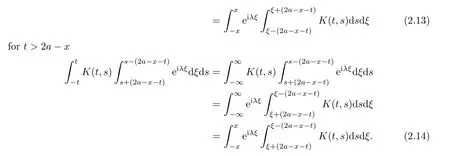
Substituting expressions(2.11)–(2.14)into equality(2.10)and then changing the denotation for integration variables,we get
Thus,putting relations(2.9)and(2.15)into equality(2.8),we find
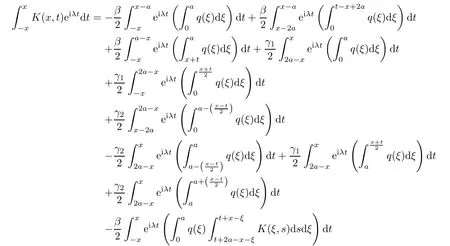
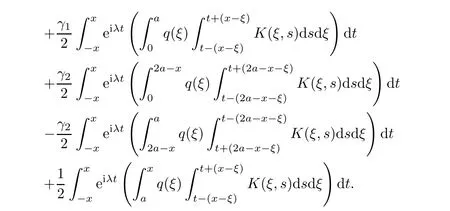
It follows from this equality that

Now,in the case of x Consequently,if the function K(x,t)vanishes for|t|>|x|and satisfies equations(2.16)and(2.18),then the function e(x,λ)constructed by means of formula(2.2)is the solution of equation(2.7)and conversely.In order to complete the proof of the theorem it suffices to show that for each fixed x ∈ (0,a)∪(a,π)the system of equations(2.16),(2.18)has the solution K(x,.)∈L1(−x,x)satisfying inequality(2.3).To obtain this,we apply the successive approximation method:set and for n=0,K0(x,t)is determined by formulas(2.17)and(2.19).Show that When n=0,expression(2.22)is true.In fact,for x For x>a,it is obtained from(2.17)that In case n=1,formula(2.22)is satisfied.Indeed,for x Since K(x,t)=0 for|t|>|x|,we can write For x>a,taking into account expression(2.21),we get Since K(x,t)=0 for|t|>|x|,it is obtained that Suppose that expression(2.22)is true for n=m.Then,it is shown from(2.21)that Consequently,the series K(x,.)converges in L1(−x,x)and its sum K(x,t)is a solution of the system of equation(2.16),(2.18)that satisfies condition(2.3).Moreover,relations(2.4)–(2.6)are obtained from expressions(2.16)–(2.19). ? Theorem 2.2 The kernel K(x,t)has both partial derivatives Kx(x,t)and Kt(x,t)∈L1(−x,x)for every x ∈ (0,a)∪(a,π)and the relations are valid: Moreover,if q(x)is differentiable on(0,π),then the kernel K(x,t)satisfies the following partial differential equation Proof Consider x Using this equality,we get Changing the variables,we find Since K(x,t)=0 for|t|>|x|and from(2.3), and since q(x)∈ L2(0,π)and σ(x)is monotonically increasing function, is obtained,where k1is a constant.Similarly,it is shown that Now,take into account x>a.When 2a−x Using K(x,t)=0 for|t|>|x|,condition(2.3),q(x)∈ L2(0,π)and the monotonically increasing function σ(x),it follows from here that where k2is a constant.Similarly,it is obtained that In the same way,it is shown that Kx(x,t)∈ L1(−x,x)and Kt(x,t)∈ L1(−x,x)for x>a and the other cases of t.Thus,we obtain that Kx(x,t)and Kt(x,t)belong to L1(−x,x)for x ∈ (0,a)∪ (a,π).Moreover,relations(2.23)and(2.24)are found by using(2.16)–(2.19). Now,assume that q(x)is differentiable on(0,π).In the case of x Consider x>a.Let us find the partial differential equation provided by the kernel function K(x,t).When 2a−x In here,changing the variables ξ+s=2θ and ξ− s=2ϑ and taking into account K(x,t)=0 for|t|>|x|,we find Now,we put x+t=2u and x−t=2v.Then,it follows from this equality that Now,similarly,let us examine the other cases of t.For x−a≤t<2a−x,we get In here,we set x+t=2u and x−t=2v.Then,we can write When a−x≤t≤x−a,we calculate Putting x+t=2u and x−t=2v in this equality,we obtain For x−2a≤t≤a−x,we have It is found by putting x+t=2u and x−t=2v in this expression that Finally,in case of−x In here,put x+t=2u and x−t=2v.This yields the following equation Now,using equality(2.26),we can write From these equalities,it follows that the function K(u+v,u−v)satisfies the equation Similarly,taking into account equalities(2.27)–(2.30),we obtain equation(2.31).In addition,if q(u)is differentiable,then K(u+v,u−v)has all the second-order derivatives.Hence,we can shift back to variables x=u+v and t=u−v in equation(2.31).Then,this yields the following partial differential equation Consequently,it is proved that in order for K(x,t)to be kernel of the integral representation determined by formula(2.2),it is necessary and sufficient that K(x,t)satisfies equation(2.25)and conditions(2.6),(2.23)and(2.24).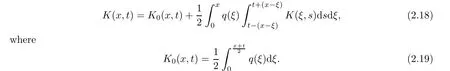
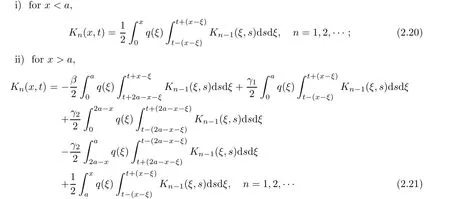
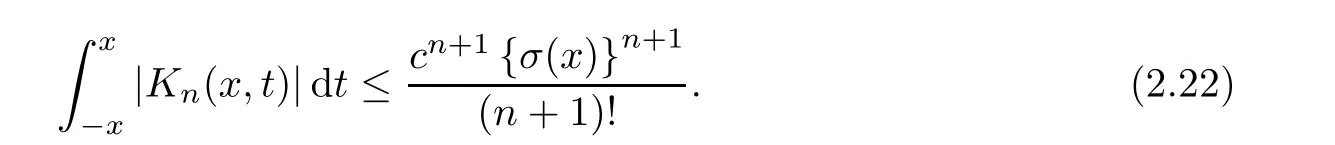
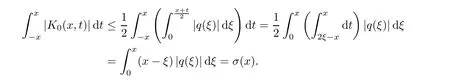
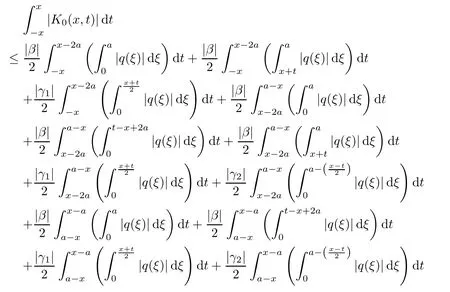
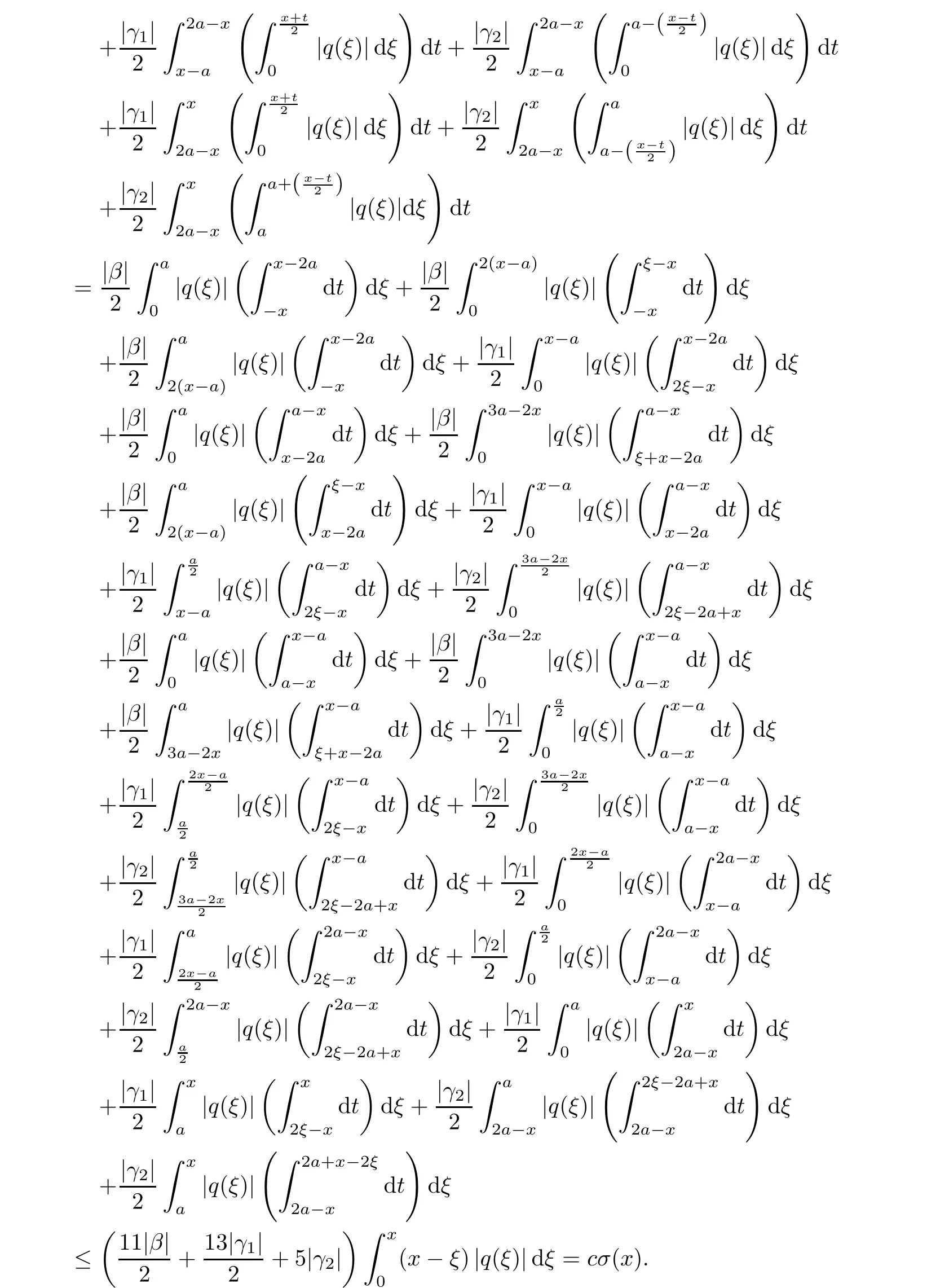
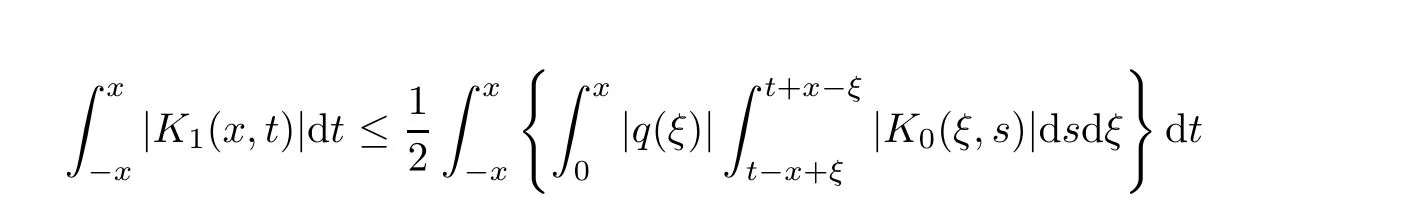
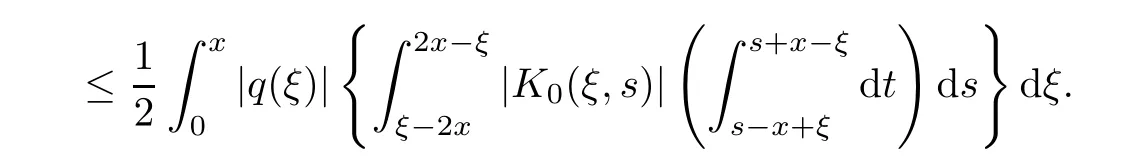

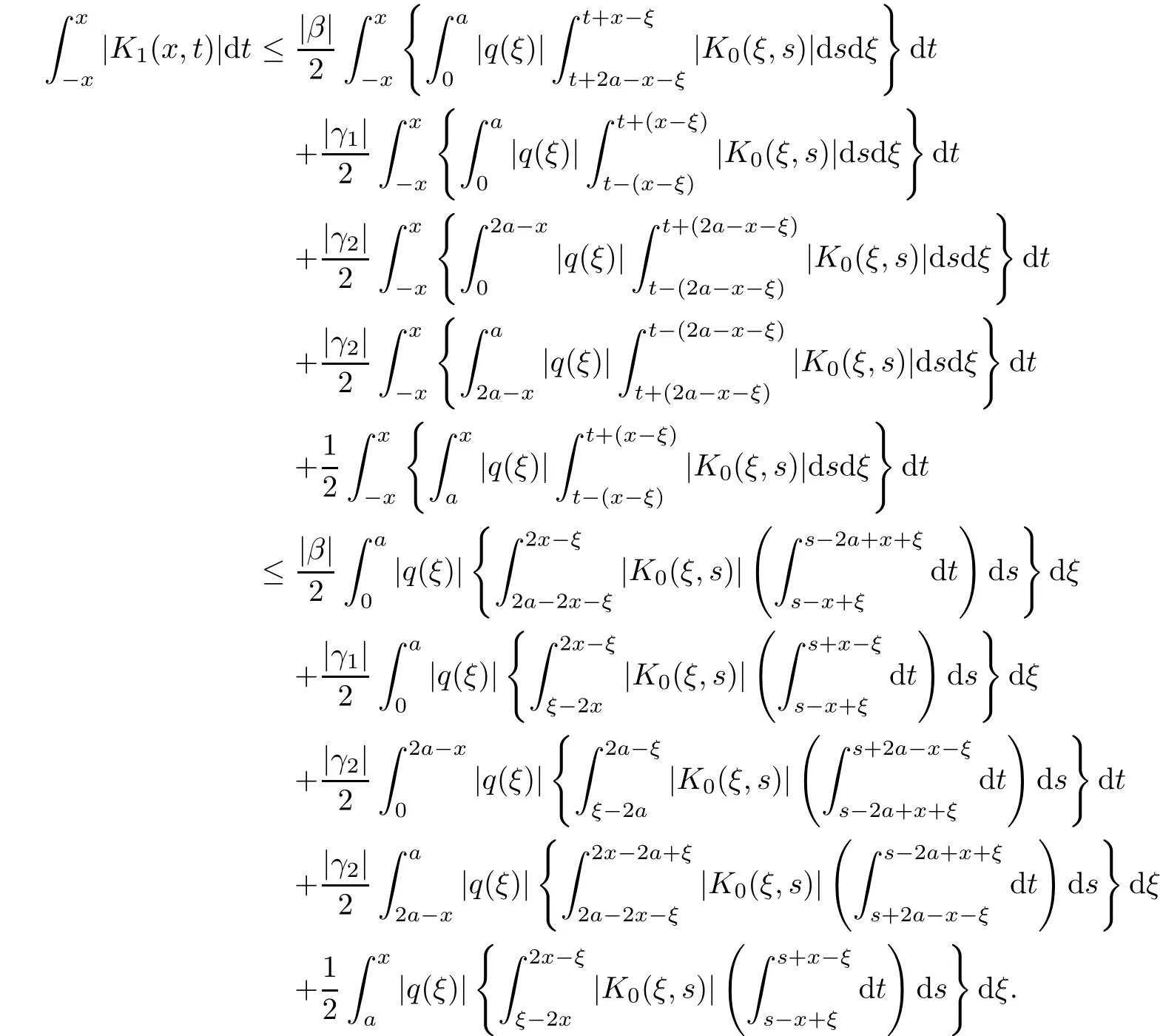
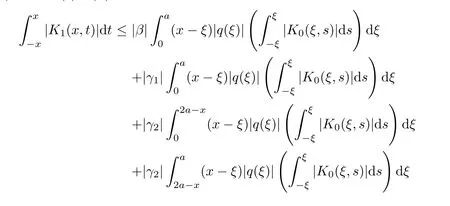

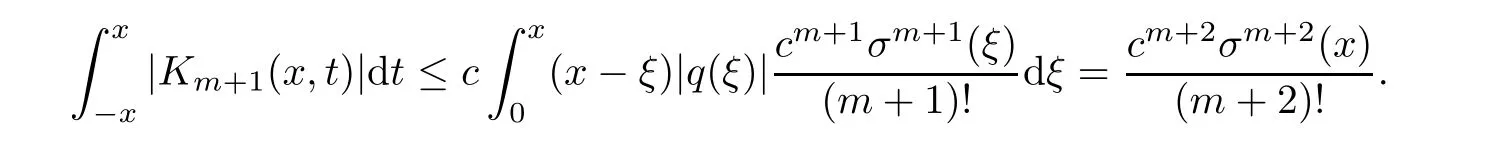
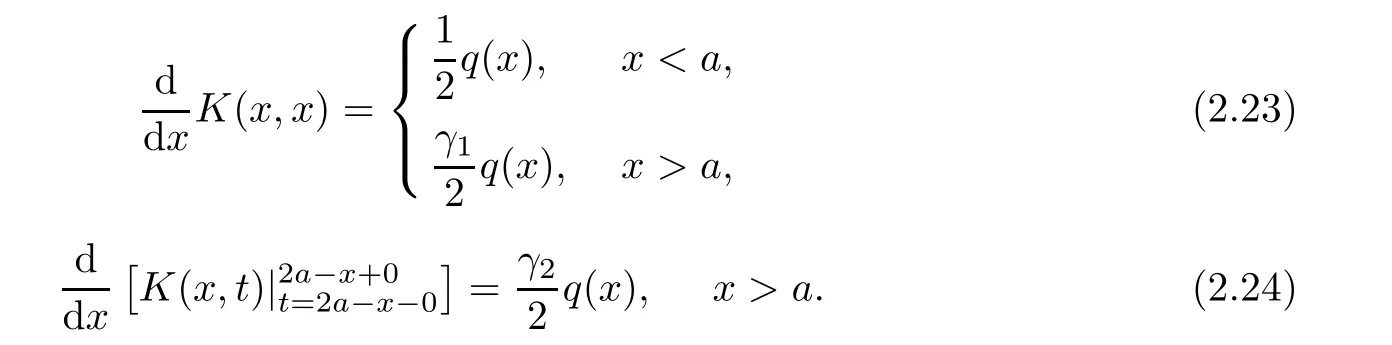

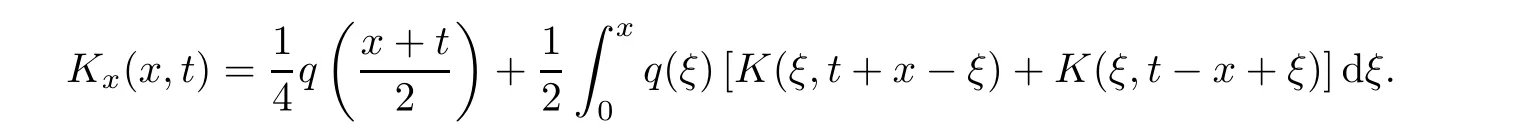
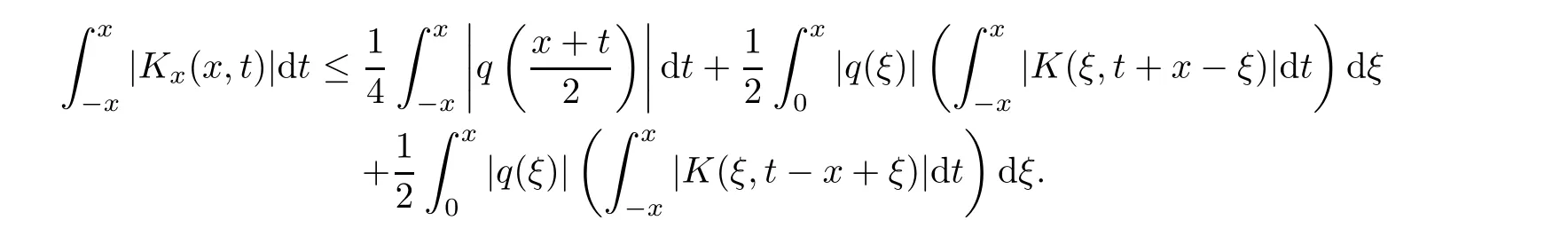
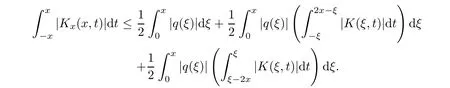
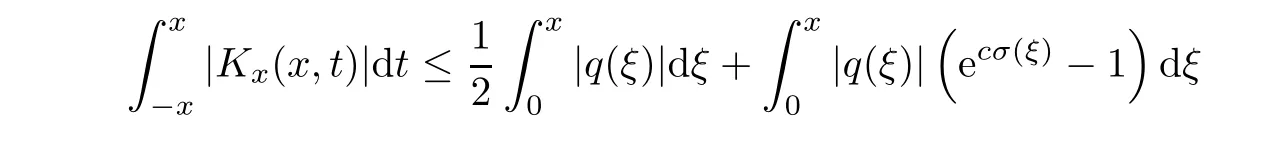
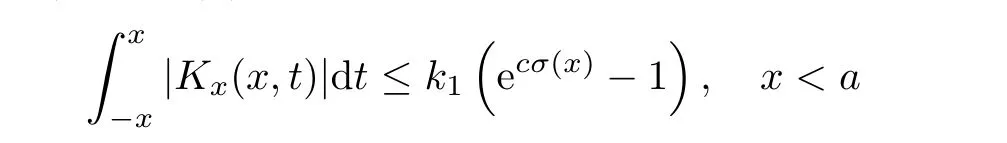
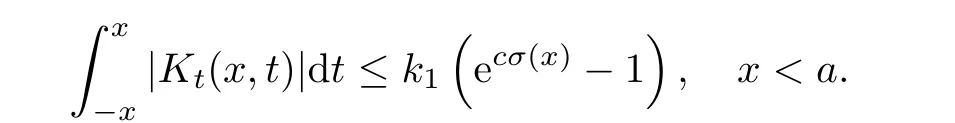
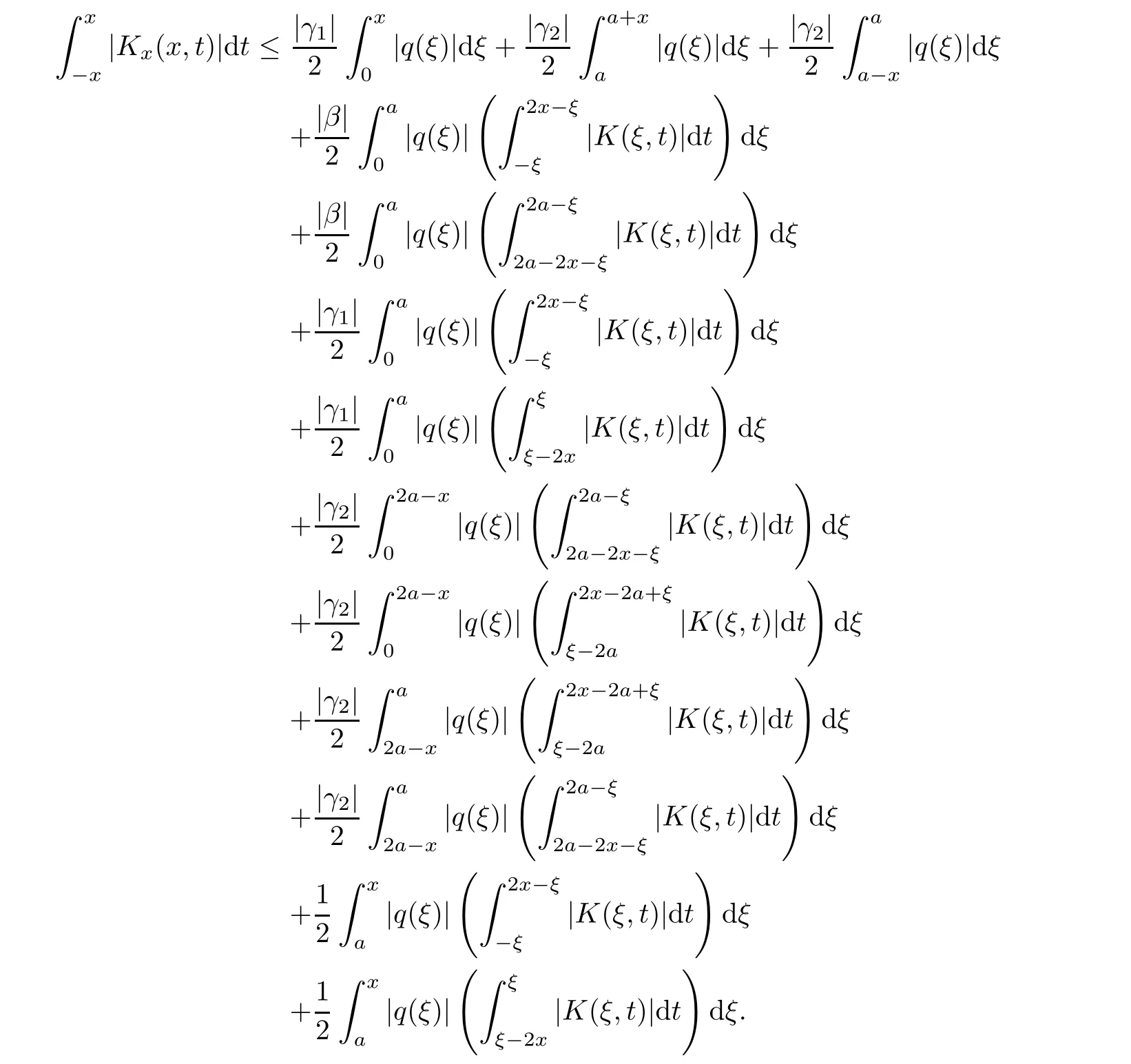
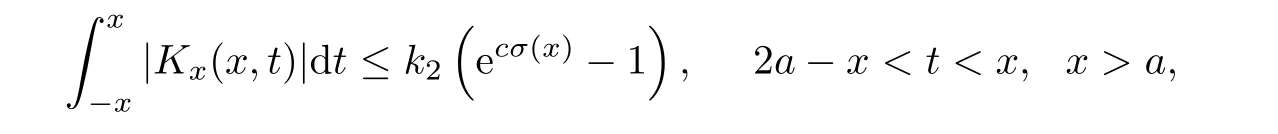
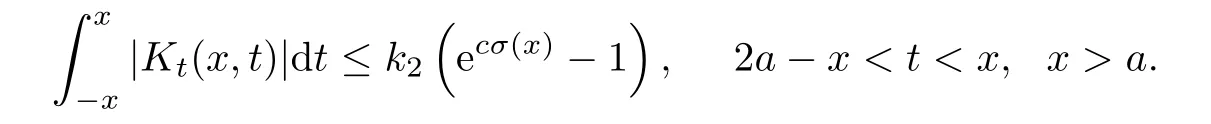

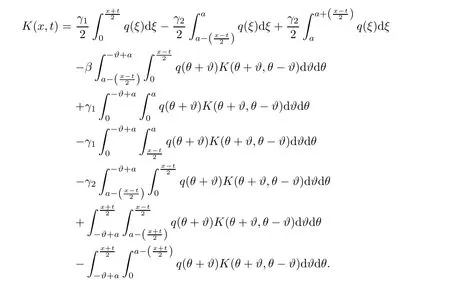
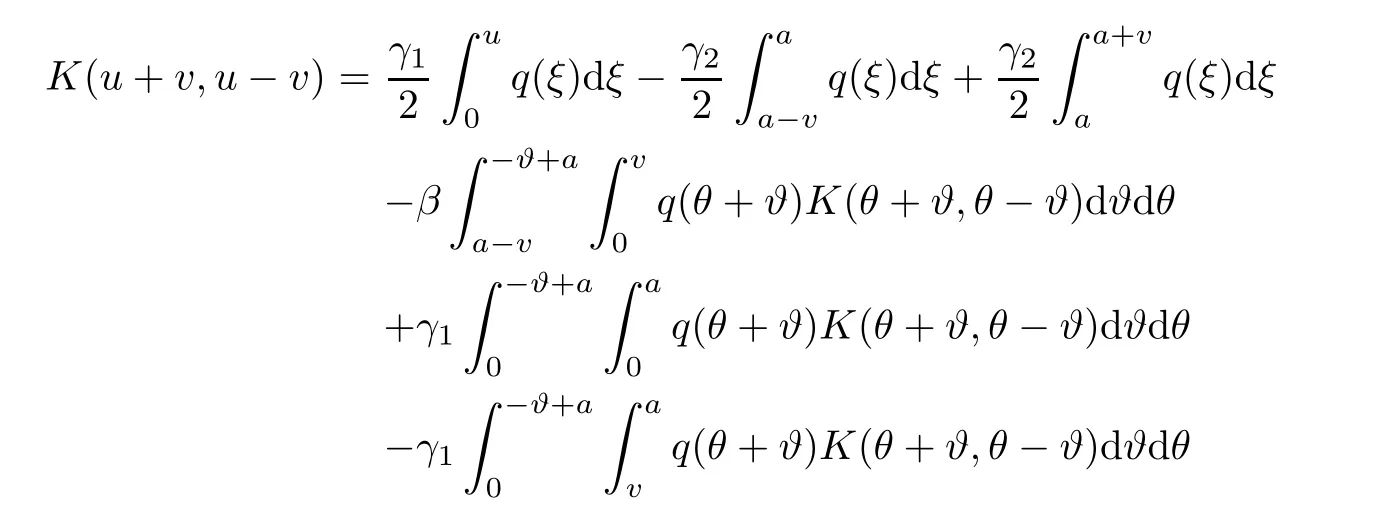
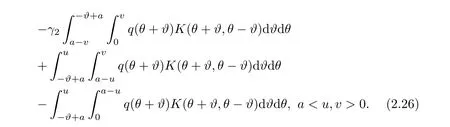
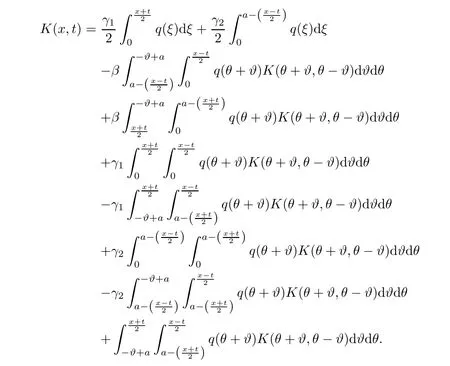

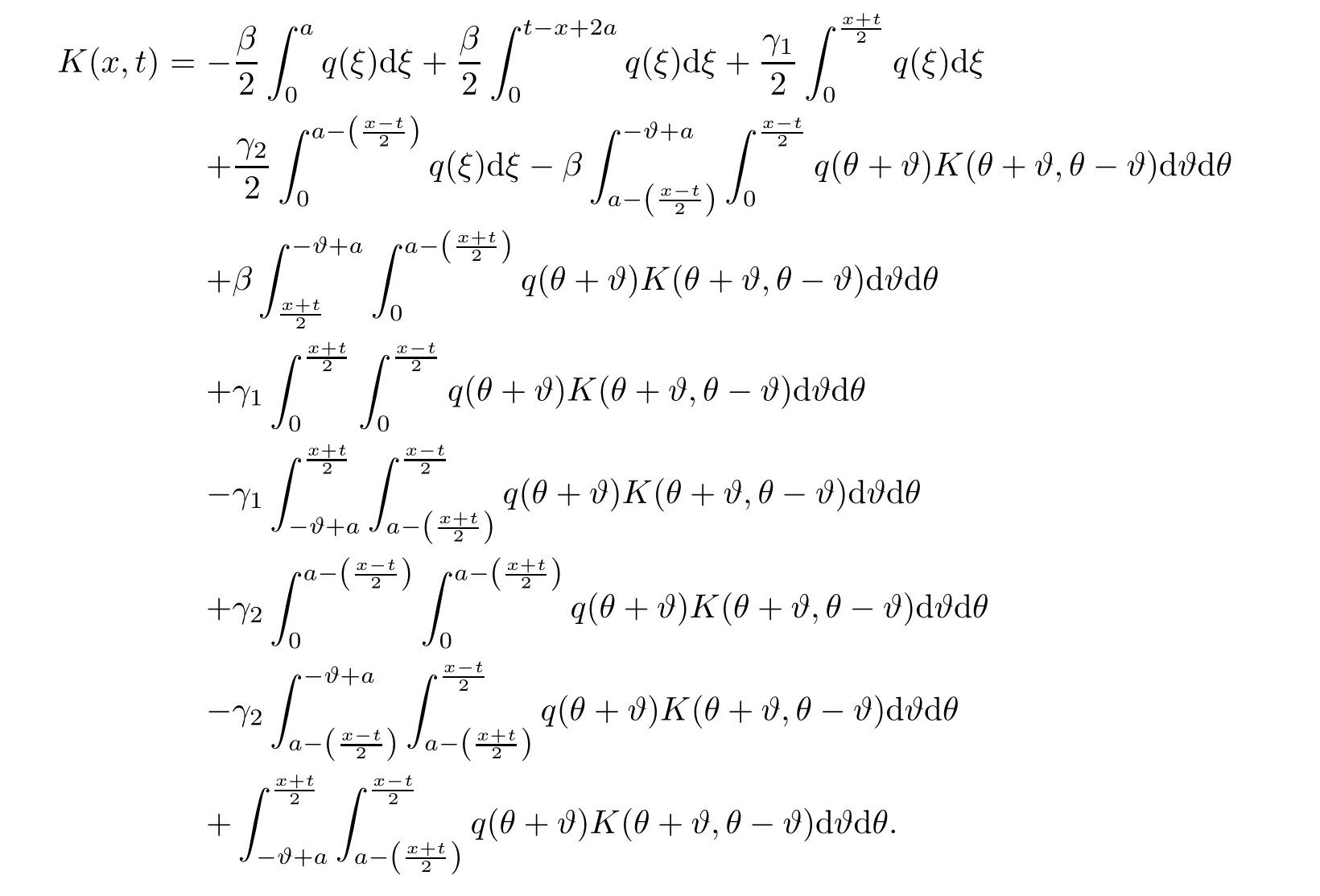

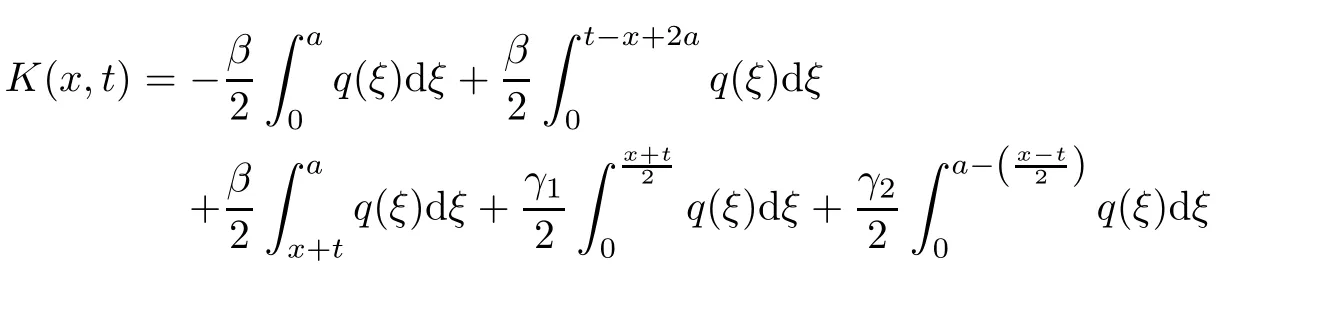
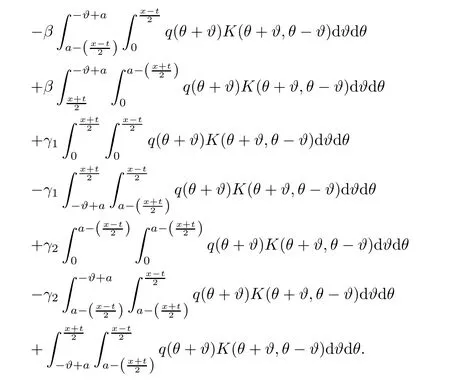
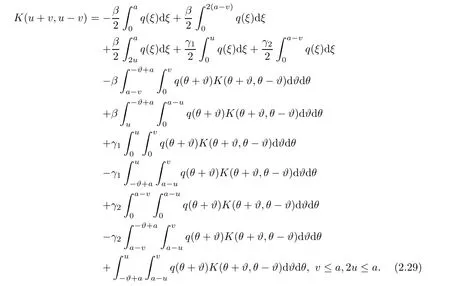

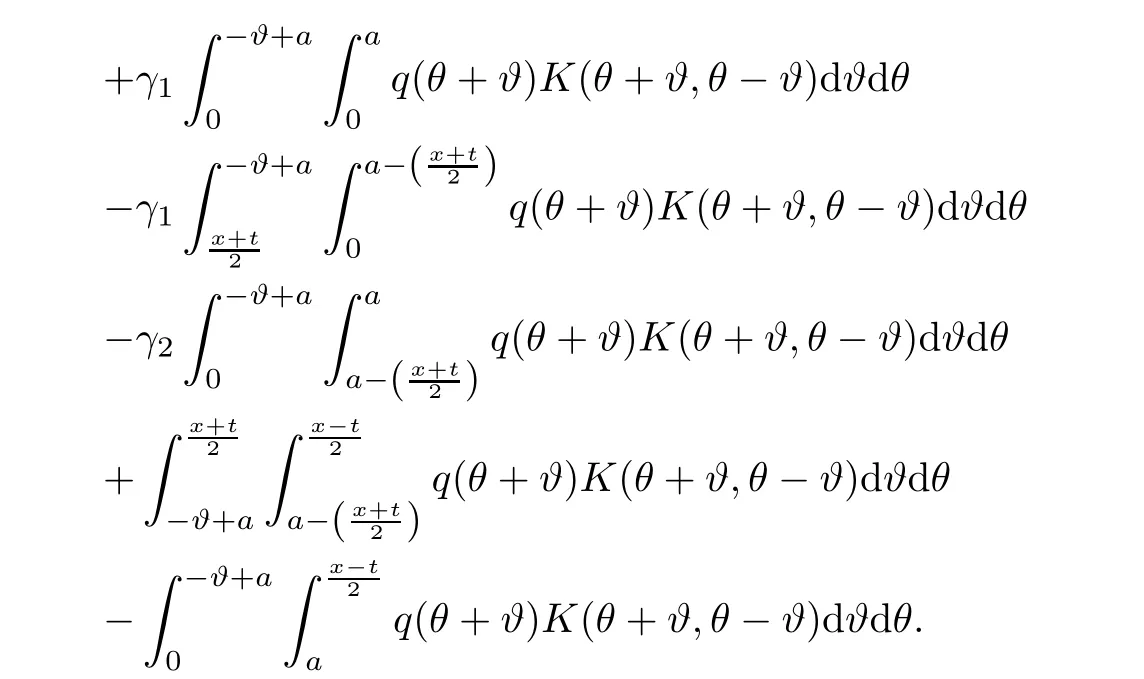
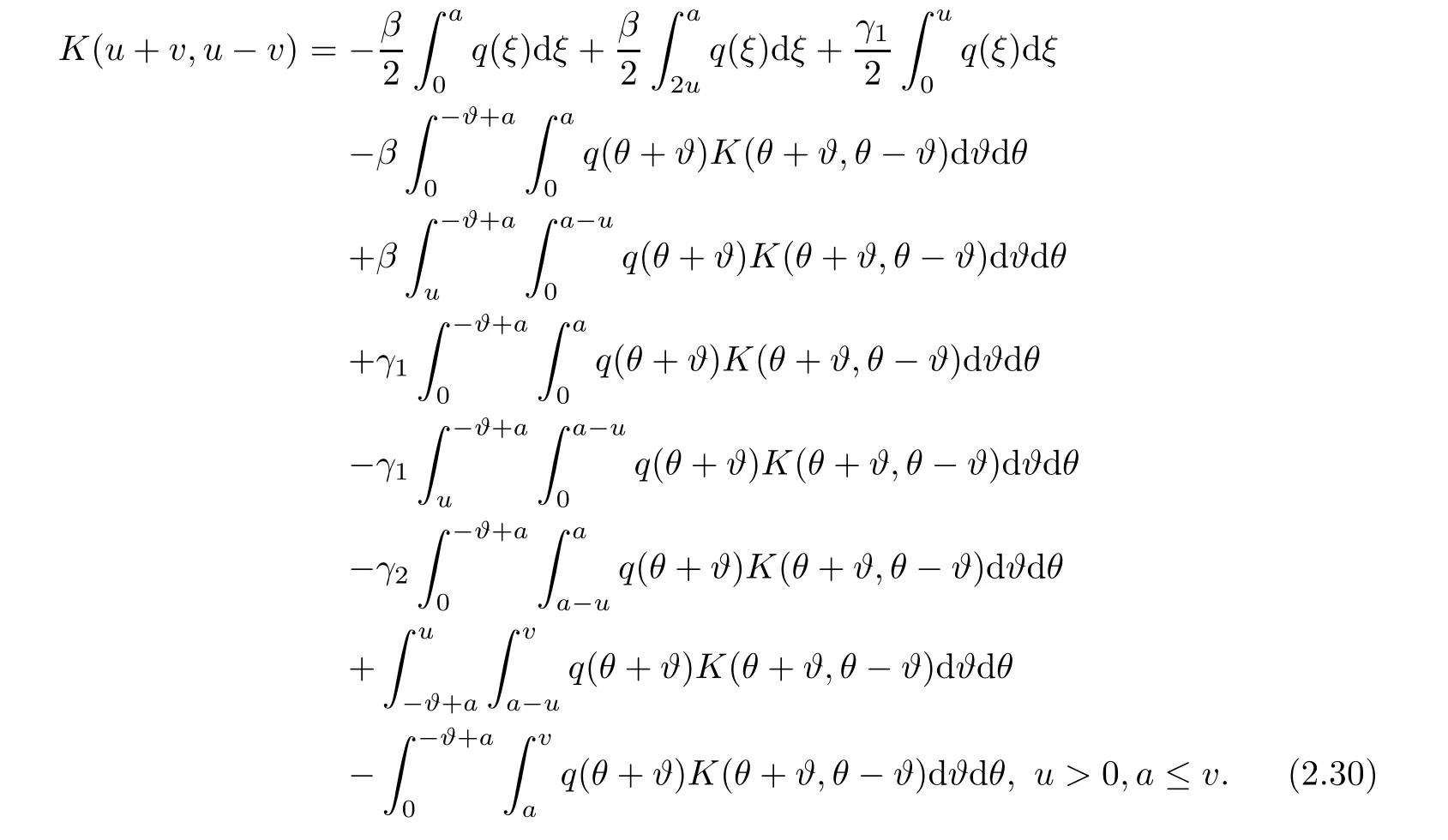

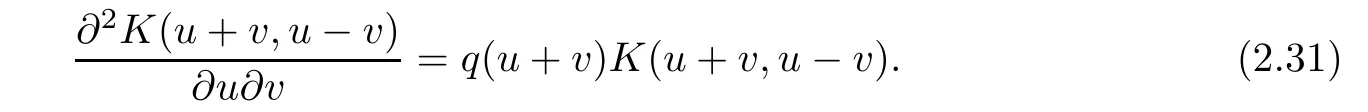
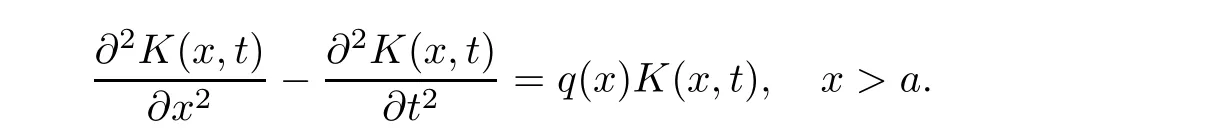
 Acta Mathematica Scientia(English Series)2018年4期
Acta Mathematica Scientia(English Series)2018年4期
