基于Boosting Tree算法的测井岩性识别模型

江凯,王守东,胡永静,浦世照,段航,王政文

(1.中国石油大学(北京)地球物理与信息工程学院,北京 102249;2.油气资源与探测国家重点实验室,北京 102249;3.海洋石油勘探国家工程实验室,北京 102249;4.中国石油新疆油田公司勘探开发研究院,新疆 克拉玛依 834000)

0 引 言

目前进行岩性识别最可靠直观的方法是钻井取心,但油田开发区取心井一般较少,且取心井段有限[1],而测井资料能提供全井段的高分辨率地下岩石物理响应信息,已成为油气藏研究的重要手段[2]。

测井岩性解释是通过分析地球物理测井资料,建立测井参数与岩石类型之间的映射关系模型,再借助手工或计算机对测井数据进行处理,最终达到识别岩性的目的[3]。目前利用测井数据进行岩性解释的方法多种多样,但总的可以归纳为基于测井曲线响应特征的定性解释方法[4]、基于测井响应方程的定量解释方法[3]、图版法[5-8]和支持向量机(SVM)[8-11]、神经网络[11-12]、决策树[13-14]等基于机器学习的智能化方法。其中定性解释方法和图版法的可靠性取决于解释人员的实践经验和剖面的复杂程度且需要人工方式进行处理,受人为因素影响大,解释效率较低,另外图版法只能利用部分测井资料,不能实现全部测井信息的有效利用;定量解释方法通过建立测井响应方程实现岩性识别,相比于定性方法可靠性更高,但其受限于地层矿物成分数量,对复杂岩性储层的适用性较差[3];基于机器学习的岩性解释方法因具有数据处理高度自动化、岩性识别智能化的特点,已成为近年来的研究热点。支持向量机的关键是核函数的选取、神经网络的难点在于网络结构设计和参数设置,决策树是一种符号学习方法,直观易于理解,以上3种方法适用条件各异,方法原理和参数设置不同,都是基于单一学习器的方法,一次学习完成后,不能对错误样本进行再学习。

Friedman等[15]在2000年提出Boosting Tree算法,其构建并结合多个决策树学习器完成分类任务以提高分类精度[15-17],在互联网知识推荐领域已得到广泛的应用。本文使用Boosting Tree算法建立岩性识别模型,并对准噶尔盆地玛北油田复杂砂砾岩储层的岩性进行识别,取得了很好的应用效果。同时本文将Boosting Tree算法与决策树、支持向量机等传统机器学习方法进行比较,结果证明基于Boosting Tree算法的岩性识别模型的性能优于其他2种算法。

1 Boosting Tree算法原理

Boosting Tree算法将多个决策树学习器进行组合,以获得比单个决策树学习器显著优越的泛化性能,其被认为是统计学习中性能最好的方法之一[18]。

1.1 决策树

Boosting Tree算法的基学习器为决策树。决策树算法是一种具有树状结构的符号学习方法,其由结点和有向边组成,结点分为代表属性测试的内部结点和代表决策结果的叶结点[19]。从根结点开始(根结点包含全部样本),对样本集合的全部属性依此进行测试,根据测试结果将样本集合划分到不同的子结点中,这时每个子结点中的样本子集都对应着该属性的一个取值或取值范围,若该子结点还可进行属性测试,则其为内部节点,否则为叶结点。如此递归对每个内部节点中的子集进行属性测试并划分,直至到达叶结点,即可获得最后的分类结果(见图1)。在岩性识别问题中,每个测井方法获得的数据即为一个属性值,某一深度对应的岩性即可认为是一个叶结点。

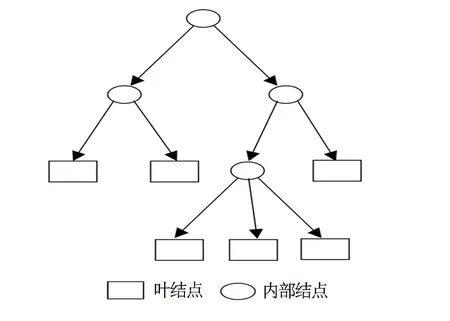
图1 决策树模型

样本属性测试的规则是决策树算法的关键。CART算法是目前应用广泛的决策树方法,其使用基尼指数来选择划分属性。假设样本集合D中共有K类样本,第k类样本所占比例为pk,即样本点属于第k类的概率为pk,1-pk即为样本点不属于第k类的概率,则样本集D的基尼指数为

k=1,2,3,…,K

(1)

在对某一属性进行测试时,需要计算这一属性的基尼指数。属性a的基尼指数为

(2)

式中,N表示人为的按属性值的大小或个数对内部结点中子集进行分块的数量(例如可将样本子集按大于或小于某一数值进行分块,此时N=2);|D|和|Dn|分别表示样本总数和第n个样本分块中的样本数;Gini(Dn)表示第n个样本分块的基尼指数。

从根结点开始,在每个内部节点上都分别计算每个属性的基尼指数,将基尼指数小的属性作为最优划分属性,可向下延伸出N个分支,如此递归直至到达叶结点结束。

1.2 Boosting Tree算法

Boosting Tree算法的基本思想是通过改变训练样本分布,学习多个决策树学习器(基学习器),并将这些学习器进行线性组合,以提高分类性能[15-17,20]。每次改变训练样本分布时,使被前一个学习器错误分类的样本权重提高,被正确分类的样本权重降低,这样被分类错误样本在下一个学习器将受到更大关注。将所有基学习器进行线性组合时,给予误差率小的基学习器更大的权值,误差率大的基学习器更小的权值,以此规则组合后即获得最终的分类器。

假设给定一个二分类的训练样本集D={(x1,y1),…,(xi,yi),…,(xm,ym)},yi∈{-1,+1),xi∈Rn,其中m为样本集大小,n为数据维数,即样本的属性个数。若训练T个弱学习器,用Dt表示第t次改变样本分布后的样本集,用Wt=(wt,1,…,wt,i,…,wt,m)表示第t次改变样本分布时所使用的样本权重,则初始时样本权重为w1,i=1/m;用ht(x)表示第t个弱学习器决策树模型,则Boosting Tree可表示为

(3)

在Boosting Tree算法中,第1个基学习器h1(x)是直接由初始样本分布训练而得,此后迭代地生成ht(x)和at。在基于样本集Dt训练下一个基学习器时,新的基学习器ht(x)和权重at应使得Ht(x)最小化指数损失函数

(4)

其中,f(x)表示对所有样本都分类正确的学习器;wt,i=exp(-f(xi)Ht-1(xi))可以被看作常数,如果将被ht(x)正确分类的样本的集合记作Ct,将错误分类的样本的集合记作Et,那么误差函数写成式(5)形式

(5)

其中,指示函数I(f(xi)≠ht(xi))定义为

(6)

对式(5)关于at求导并置零得

(7)

其中,et表示ht(x)在样本集Dt上的分类错误率,其定义为

(8)

式(7)为基于样本集Dt训练得到的基学习器ht(x)的权重at的更新公式。根据式(4),令

wt+1,i=wt,iexp(-f(xi)atht(xi))

(9)

得到该权重更新公式(9)。

由式(7)可以看到,当ht(x)在样本集Dt上的分类错误率et越小,则at越大,即表明对全部基学习器进行线性组合时,分类错误率小的基学习器会有更大的权值;而由式(9)可知,当分类错误率et<0.5,则at>0,此时若样本(xi,yi)分类错误,即f(xi)≠ht(xi),则wt+1,i=wt,ieat>wt,i,这表明被ht(x)分类错误的样本将在训练下一个基学习器ht+1(x)时赋予更大的权值。

2 岩性识别模型设计

2.1 样本构建

使用机器学习方法所构建的岩性识别模型都需要多维数据作为样本进行训练,Boosting Tree算法作为一种有监督的机器学习方法还需要给样本加上准确可靠的标签。所以样本构建的关键是测井属性的优选和岩性标签的合理选择。

在使用Boosting Tree算法进行岩性识别时,所输入的测井属性组合直接影响预测精度,因此需要进行测井属性优选。根据不同测井属性对地下岩性的敏感度,选取准噶尔盆地玛北油田目的层的自然伽马、自然电位、井径、冲洗带电阻率、侵入带电阻率、原状地层电阻率、密度、补偿中子、声波时差等9个测井参数采用交叉验证法进行试验,发现井径对岩性识别精度提高的贡献率很低,为了提高岩性识别模型的计算性能,故舍弃该测井参数选取剩下8个测井参数作为样本属性值。

根据录井资料,准噶尔盆地玛北油田目的层的岩石类型主要为泥岩、砂质泥岩、含砾泥岩、泥质粉砂岩、褐色砂砾岩、灰色砂砾岩和含砾粗砂岩7种岩性,其中后2类为储集层。在实际测井解释中,往往更加关注储层岩性的精细化分,故本文将泥岩、砂质泥岩、含砾泥岩、泥质粉砂岩统一归为泥岩一类,同时为了方便编程处理,用数字标签1表示泥岩,用数字标签2表示含砾粗砂岩,用数字标签3表示灰色砂砾岩,用数字标签4表示褐色砂砾岩。根据录井资料,在每个深度的测井数据后面加上岩性数字标签,即得到标记后的测井数据样本集。

2.2 数据预处理

不同的测井方法测得的数据拥有不同的量纲和属性值数量级,如果直接将测井数据作为输入训练岩性识别模型,那么他们对结果的影响程度是不一样的。为了消除这种系统性误差,就需要对数据进行标准化处理(见图2)。

(1) 数据的中心化。得到均值为0,标准差为1的数据集,计算过程为

(10)

式中,x为样本数据;μ为样本数据均值;σ为样本数据标准差。

(2) 数据的归一化。将测井数据样本集的所有属性值化到(-1,1)之间。

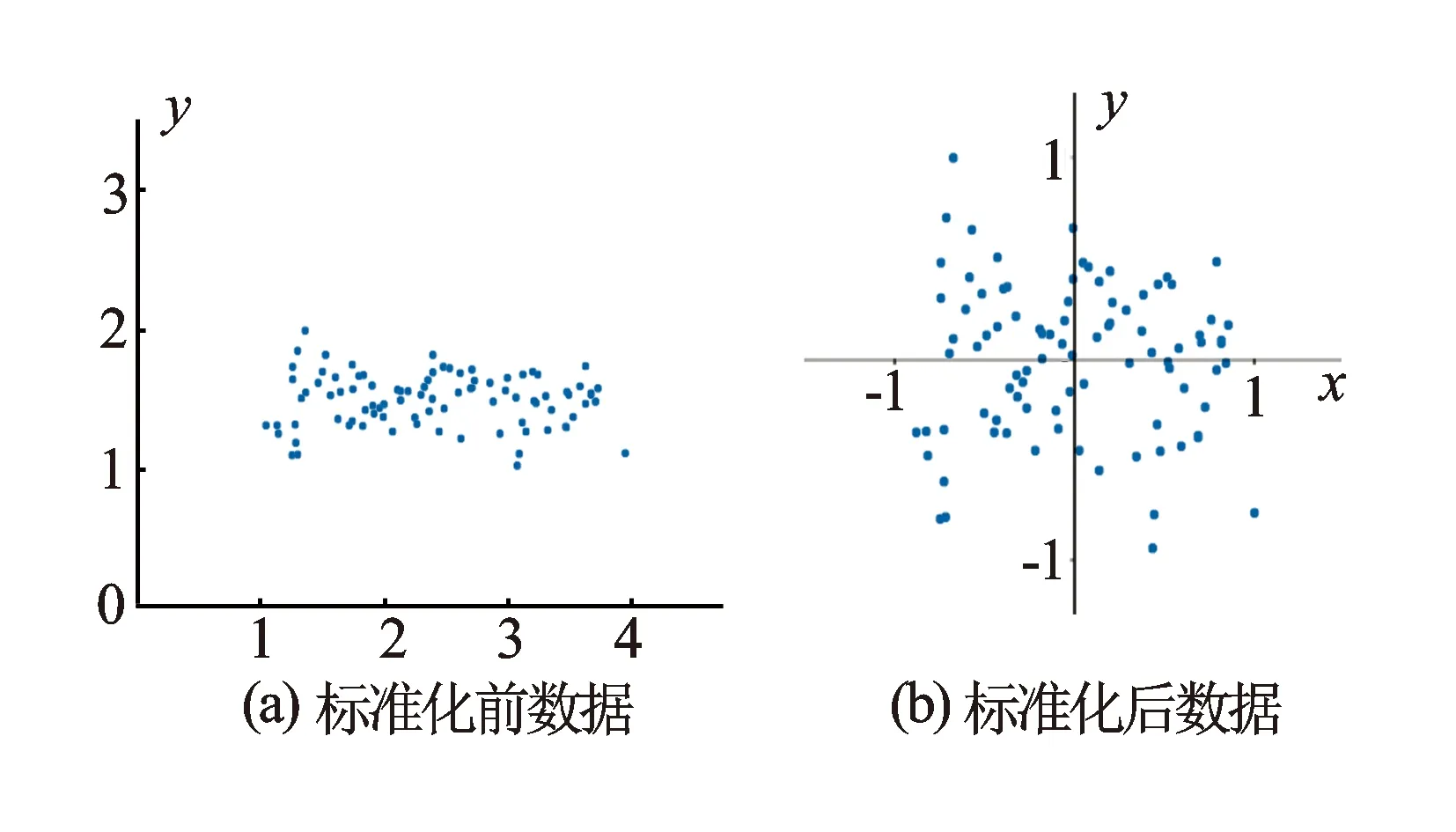
图2 数据标准化前后变化示意图

2.3 模型参数和模型评价指标

使用交叉验证法对模型参数进行寻优。k折交叉验证就是将样本数据集分为大小相同的k份,其中k-1份作为训练集进行模型训练,剩下的1份作为验证集检验模型在训练集上的分类性能。该过程重复k次,使得每份数据恰好用于验证集一次,模型在训练集上的总误差是这k次验证集误差的平均。

基于Boosting Tree算法的岩性识别模型的参数包括基学习器决策树模型最大深度Depth和基学习器个数N。Depth代表决策树模型结点的最大延伸长度,其值过大,就会对数据过拟合,其值过小则会欠拟合,这2种情况都会降低模型的泛化能力。使用交叉验证法对Depth的值进行寻优,确定Depth的值取6;基学习器个数N的值过大不仅会出现过拟合现象降低模型泛化性能,程序的计算时间也会迅速增加(见图3)。图4是采用交叉验证法得到的模型误差与基学习器个数N之间的变化关系图,由图可知当N超过200时,模型误差不再有明显降低,故确定基学习器个数N为200。

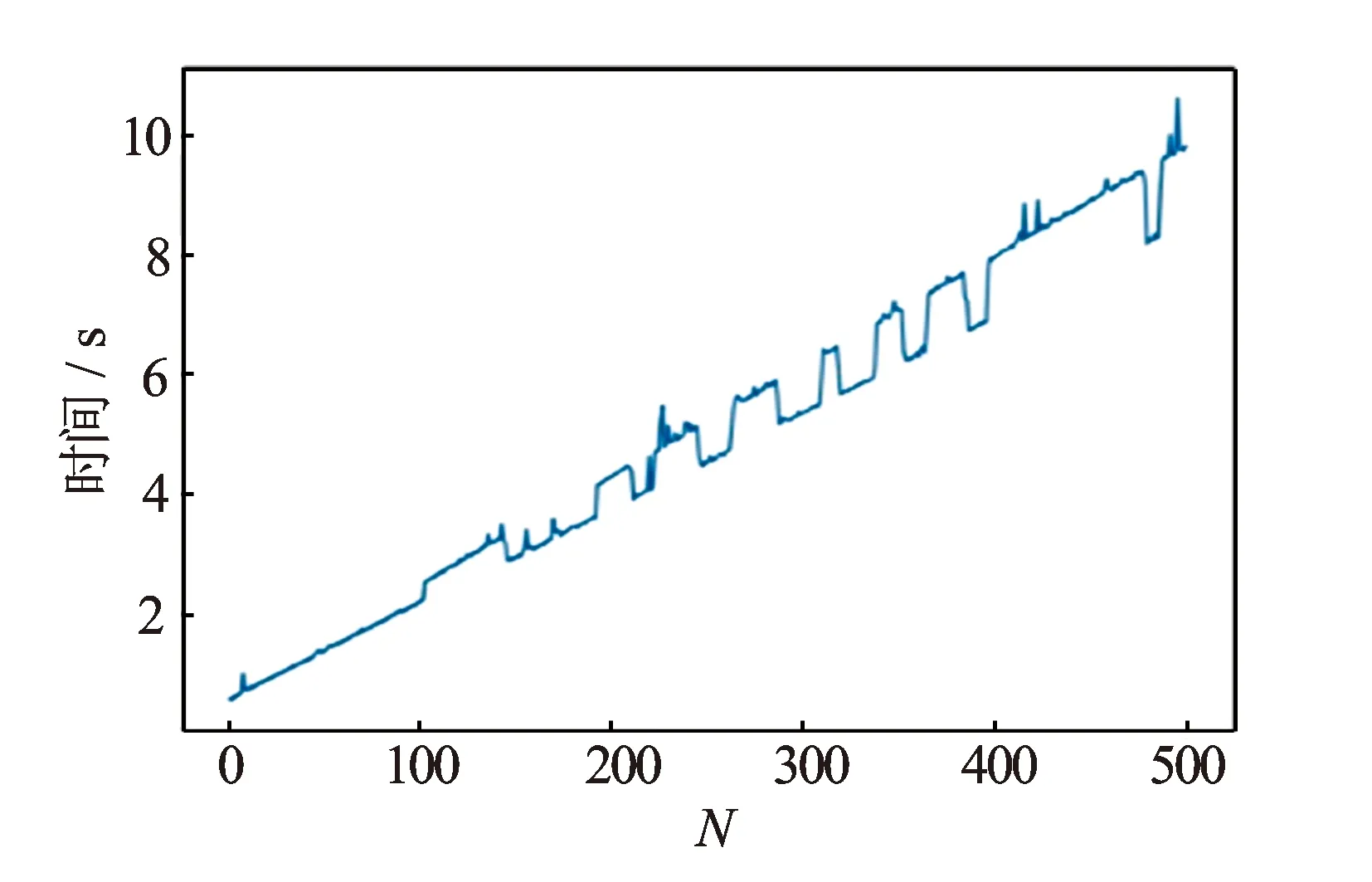
图3 程序运行时间随基学习器个数变化关系图

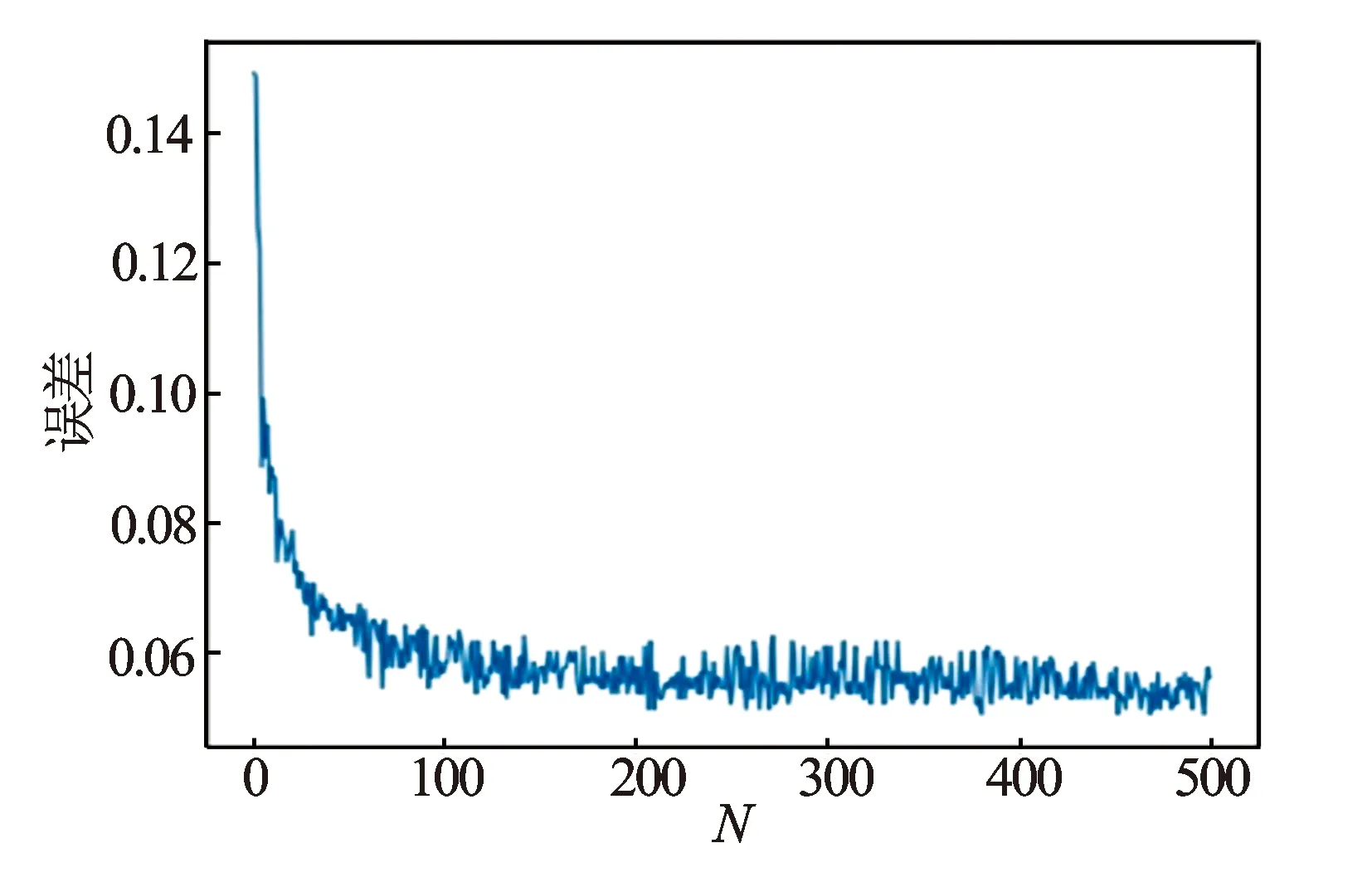
图4 模型误差随基学习器个数变化关系图

当使用已经训练好的岩性识别模型对新井进行岩性解释时,需要评价模型的识别效果。已有文献[8,10-11]大多使用正确率作为模型的性能度量,认为岩性识别正确的样本数占样本总数的比例越高则模型识别效果越好。在实际测井岩性解释时,往往希望在保证正确率的情况下,尽可能全面的将储层岩性识别出来,故本文同时使用正确率和查全率作为岩性识别模型的评价指标,查全率表示属于某一类别的样本被正确识别的比例,储层岩性的查全率越高则认为模型识别效果越好。

3 应用实例

3.1 区域概况

玛北油田位于准噶尔盆地西北缘断阶带下盘,属玛湖凹陷北斜坡带,构造格局表现为东南倾的平缓单斜,局部发育低幅度平台、背斜或鼻状构造,断裂较少[21]。其目的层三叠系百口泉组是一套扇三角洲碎屑沉积,主要岩性为粉砂质泥岩、含砾泥岩、泥质粉砂岩、褐色砂砾岩、灰色砂砾岩和含砾粗砂岩。研究区目的层段具有岩石类型多,岩性内部结构复杂,储集层低孔隙度低渗透率,非匀质性强的特点,给岩性解释带来较大挑战[21-23]。

3.2 应用效果

本文共使用研究区6口井对应目的层段的4 850个测井数据,每个测井数据的采样深度间隔为0.125 m。将1～5号井的4 106个测井数据作为训练集用于训练岩性识别模型,训练集中泥岩、含砾粗砂岩、灰色砂砾岩、褐色砂砾岩的样本比例分别为32.7%、5.9%、38.4%、23.0%(见表1)。将岩性齐全的6号井的744个测井数据作为测试集以验证Boosting Tree算法的岩性识别效果,同时将其结果与使用决策树、支持向量机算法的岩性识别结果进行比较,结果见表2和表3。

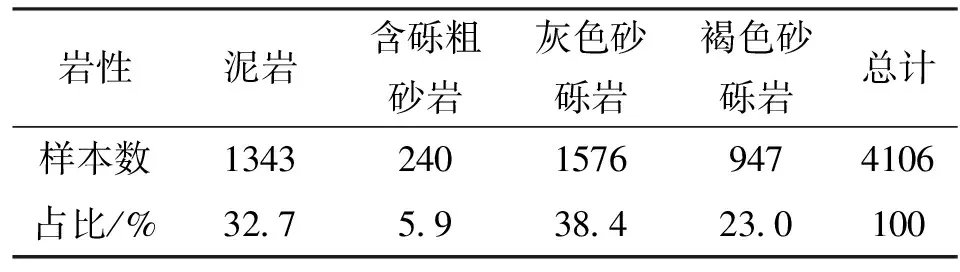
表1 训练样本集岩性类别分布表

通过与录井分析得到的准确可靠岩性解释结果进行比较,使用Boosting Tree算法对准噶尔盆地玛北油田6号井目的层段岩性识别的正确率达到89.1%,高于决策树算法的84.7%和支持向量机算法的86.8%。研究区目的层的储集层段岩性为灰色砂砾岩和含砾粗砂岩,其中Boosting Tree算法对灰色砂砾岩的查全率达到88.0%,远高于决策树算法的73.7%和支持向量机算法的78.5%。而对于含砾粗砂岩,3种算法均没有对其做出有效识别,这是因为玛北油田目的层含砾粗砂岩段为薄层,可用的样本数很少,仅占训练集样本总数的5.9%,这就造成样本类别的不均衡,使占比较高的岩性类别淹没掉岩性占比较低的岩性类别信息。综合来看,Boosting Tree算法相比于其他2种算法对储集层岩性的识别效果更好。对于非储集层中的泥岩,3种岩性识别算法的查全率均大于90%,其中Boosting Tree算法对泥岩的识别效果优于决策树和支持向量机,其查全率达到96.9%.而对于褐色砂砾岩,Boosting Tree算法的查全率为84.3%,略低于决策树和支持向量机的91.2%。图5为准噶尔盆地玛北油田百口泉组6号井岩性识别结果对比图,从图5中可以直观地看出基于Boosting Tree算法的岩性识别模型在玛北油田复杂砂砾岩储层的岩性识别中取得了较好的应用效果,且应用效果优于决策树算法和支持向量机算法。表3为与决策树算法、支持向量机算法的性能比较,虽然Boosting Tree算法在训练集和测试集上的岩性识别正确率都高于其他2种算法,但由于其是多个基学习器的组合,程序运行时间相对于其他两种算法更长,在程序运行时间很短的情况下,岩性识别模型时间成本的增加并不会对岩性解释过程产生太大影响。

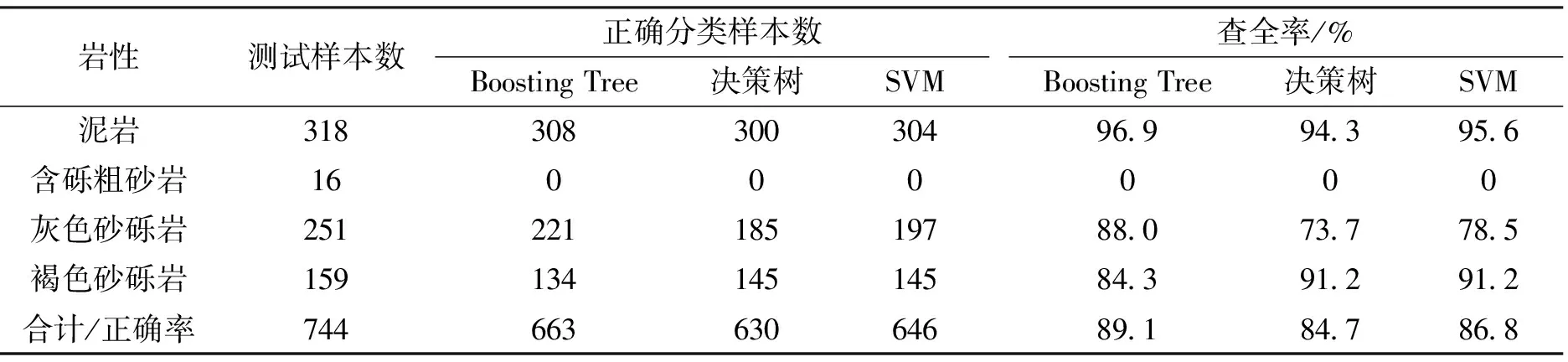
表2 玛北油田6号井不同算法岩性预测结果比较

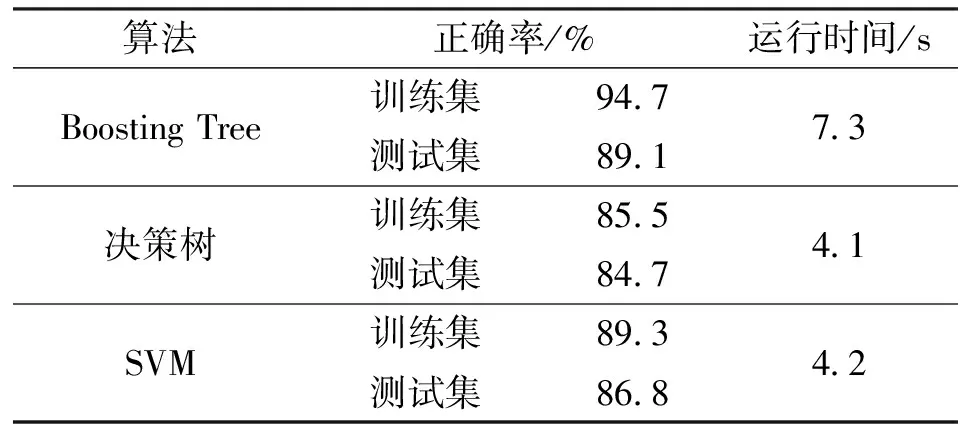
表3 不同算法性能比较

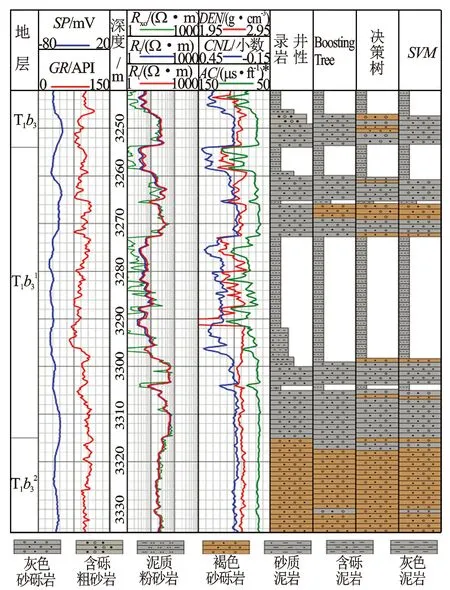
图5 准噶尔盆地玛北油田百口泉组6号井岩性识别结果对比*非法定计量单位,1 ft=12 in=0.304 8 m

4 结 论

(1) 提出了一种基于Boosting Tree算法的岩性识别模型,并在准噶尔盆地玛北油田对复杂砂砾岩储层进行岩性识别试验,取得了很好的效果,这说明使用Boosting Tree算法识别复杂砂砾岩储层岩性是一种有效的手段,也为地球物理测井解释提供了新思路。

(2) 测井属性优选、数据预处理和模型参数选择对基于Boosting Tree算法的岩性识别模型的应用效果有直接影响,需要根据专业知识优选出合适的测井属性,对测井数据进行预处理和使用交叉验证法确定最优的模型参数。

(3) 使用Boosting Tree算法进行岩性识别能够实现数据处理的高度自动化、岩性识别的智能化,其识别效果主要依赖于模型参数的选择,而降低了对解释人员实践经验和专业知识的要求。

(4) 基于Boosting Tree算法的岩性识别模型对复杂砂砾岩储层的应用效果比传统机器学习方法决策树、支持向量机更好,但由于其是多个基学习器的线性组合,运行程序的时间成本更高。