玄武岩纤维混凝土抗压强度和劈拉强度的研究

汪 炅

建德市建筑业管理处 浙江 建德 311699

1 研究背景

混凝土作为土木工程中广泛使用的建筑材料，具有较好的力学性能，但是随着工程技术应用的不断深入，其力学相关基本性能的不足也逐渐暴露出来。其中由于仅为抗压强度十分之一的较低的抗拉强度特征，致使构件受拉过程中易出现裂缝，直接降低了构件的耐久性，减小了混凝土材料的应用范围。

以提高混凝土材料工程力学性能为目标，破解混凝土材料使用的不足，多年来学者对混凝土材料的性能进行相关改良并取得阶段性成果，如加外加剂、调整配合比、改进制作工艺和养护方法等。

由于科学技术的进步和实际工程的需要，许多学者试着将其他材料（各类纤维、粉末等）掺入混凝土以提高其使用功能，其中一种就是纤维混凝土，即砂石、水泥等材料中混入无机或有机纤维形成复合材料，这种材料一方面利用混凝土的抗压性能，另一方面利用纤维良好的抗拉性能，将各自材料性能都发挥了出来。

H.F.Porter首先考虑使用钢纤维这类无机纤维混入混凝土中，以提高混凝土的抗拉能力，并提出一些相应的处理方法[1-2]。后来，J.P.Romualdi等发表的《关于纤维混凝土增强理论的研究报告》促进了这一行业的快速发展，聚酰胺纤维、聚丙烯、天然植物纤维等均被尝试作为混凝土的掺合料[3-4]。

玄武岩纤维是在1 400～1 500 ℃高温中，将玄武岩矿石熔融，然后通过拉丝漏板将熔融后的玄武岩矿石浆制成短切纤维[4]。玄武岩矿石为典型火山岩矿石，热稳定性和化学稳定性均较好，具体性能如下：质量轻、吸湿性低、耐腐蚀、导热系数低、断裂强度高、弹性模量高、伸长率低。同时玄武岩纤维有着优良的加工性能，也是典型的绿色环保材料。与建筑材料中常用的碳纤维材料相比，玄武岩纤维综合性能与碳纤维综合性能基本一致，而价格则便宜很多[5]。

基于此，本文以短切玄武岩纤维为研究对象[6]，研究玄武岩纤维体积掺量对混凝土抗压性能和抗劈裂性能的影响。

2 纤维混凝土增强机理

纤维混凝土增强机理理论现阶段主要包括两大类理论，即复合材料理论和纤维间距理论，其分别源于复合材料混合法则和纤维基体黏结理论，从不同方面对纤维的增韧作用进行解释。

2.1 复合材料理论

复合材料理论是将多种材料混合而成的材料整体视为一个多相多界面的系统，而该系统的各方面性质是各个相共同作用产生的结果。由材料力学混合定律出发，把纤维和混凝土视为一个整体，通过两者相互作用，使得混凝土的强度和弹性模量都有所改善。对简单复合材料，可以假定基体材料为各向同性、纤维平行受力方向的纤维与基体之间无相对滑移，在弹性范畴内，按叠加原理有：

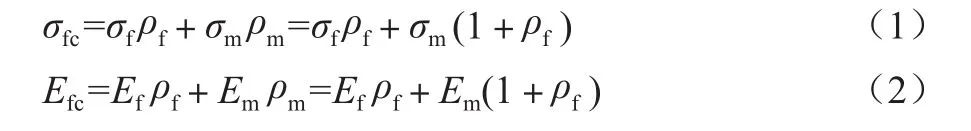
式中：σfc、σf、σm——复合体的应力、纤维的应力、水泥基体的应力；

Efc、Ef、Em——复合体的弹性模量、纤维的弹性模量、水泥基体的弹性模量；

ρf、ρm——纤维的体积率、水泥基体的体积率。

式（1）、（2）表明，在变形一致的情况下，纤维应力与水泥基体应力之比等于纤维弹性模量与水泥基体弹性模量之比，因此若要增强复合材料的总体强度与弹性模量，纤维的强度及弹性模量必须大于水泥基体的强度和弹性模量，同时可以看出，纤维单位含量越多，自身性能越好，则对复合体增强效果越显著。

本文主要研究短切玄武岩纤维复合材料，需要考虑短切纤维产生的不连续性影响，进一步可以得到下式：

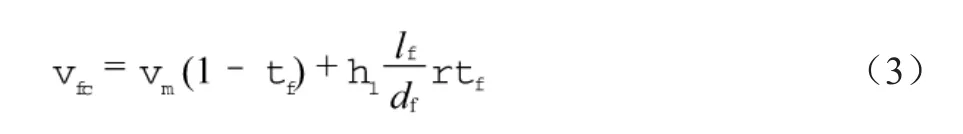
式中：lf——纤维长度；

df——纤维直径；

ηl——有效黏结长度系数。

假定纤维在混凝土中随机分布排列，即可能是一维定向分布或二维乱向分布。但对试验中采用短切纤维制作的复合混凝土来说，由于其短小，故可以认为纤维处于三维乱向分布。增强效果明显，则表明纤维方向与受力方向一致；增强效果薄弱，则说明两者方向垂直。为了方便，可以用纤维方向有效系数表示纤维分布方向与增强效果之间的关系。

2.2 纤维间距理论

纤维间距理论是基于线弹性断裂力学，假定混凝土内部存在大量缺陷，在外力作用下，这些微缺陷进一步生长延展形成分散裂纹，而若干分散裂纹进一步扩展贯通为一个宏观裂纹，从而导致混凝土最终破坏。在这个过程中，由于抗拉能力较强的纤维加入，可以有效提高复合体对各级别裂纹扩展的抵抗能力，从而达到增强作用。该理论不足之处就是，假设纤维分布均匀，若分布不均匀，纤维间距理论即失去意义。所以，在实际中，纤维分布是否均匀，是这类混凝土力学性质优劣的关键所在。

3 试验材料及试验方法

选用P.O 42.5水泥，其28 d抗压强度为48.3 MPa，28 d抗折强度为8.2 MPa。采用细度模数为2.5～ 2.6的中砂为细骨料，其表观密度为1 996 kg/m3。采用粒径5～27 mm连续性级配的碎石为粗骨料，其表观密度为2 737 kg/m3。采用减水率为40%的西卡聚羧酸系高效减水剂。短切玄武岩纤维长度在30 mm左右，单丝直径约15μm，密度2.7 g/cm3，弹性模量为95～120 MPa，抗拉强度为3 300～4 500 MPa，断裂延伸率为2.5%～30.0%。

本试验采用的相关配合如表1所示。立方体抗压试验和立方体劈拉强度试验相关试样尺寸、制备方法及实验参数，均参照《普通混凝土力学性能试验方法标准》。抗压试验、劈裂试验均采用100 mm×100 mm×100 mm立方体试件，每组3个试样，标准养护28 d。其中，劈拉强度尺寸折算系数对于普通混凝土取为0.85，对于纤维混凝土取为0.8。最大值和最小值分别与中间值之差至少有一个不大于中间值的15%，则取中间值作为该组试件的抗压强度值；如果两者与中间值之差均大于中间值的15%，则判断该组试验结果无效。

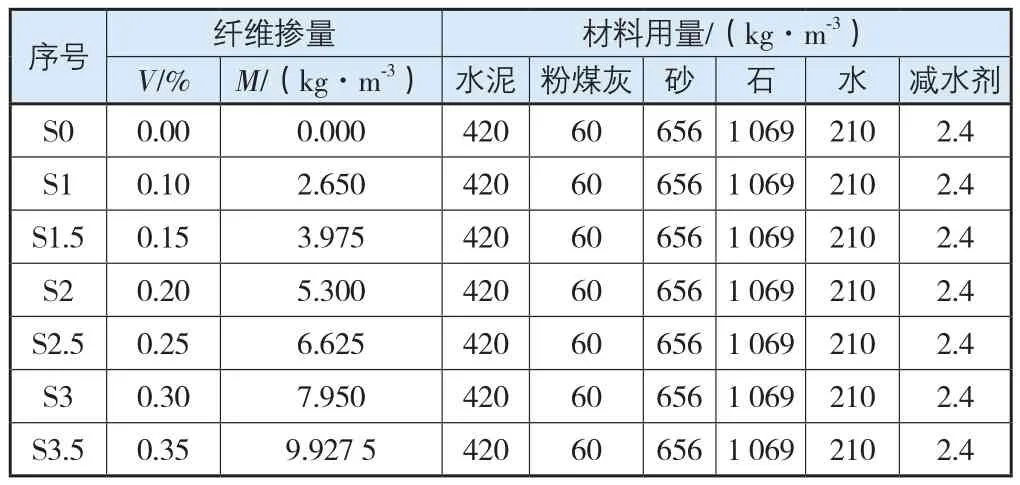
表1 不同组试件制备材料用量

4 试验步骤

1）擦净待测试件后检查外观并测量尺寸，精确到l mm。试件承压面的不平整度要求误差不大于0.5 mm/ 100 mm，相邻两面的不垂直度应小于等于1°。

2）将试件放置于载物台上，轴心对准压板中心，检查无误后开动试验机，当压板接近试件上表面时，调整支座位置，以保证不产生弯矩，达到受力均匀目的。

3）加载速度要保持连续、均匀，立方体抗压强度试验加荷速度取12～18 kN/s之间，立方体劈拉强度试验加荷速度取0.05～0.07 kN/s之间。

4）记录显示器中的荷载极值，精确至0.1 MPa。混凝土立方体试件的抗压强度计算公式如下：

式中：fcu——混凝土立方体试件抗压强度，MPa；

F——试件破坏荷载，N；

A——试件承压面积，mm2。

混凝土立方体试件的劈拉强度计算公式如下：

式中：fts——混凝土立方体试件劈拉强度，MPa。

5 试验结果及分析

由立方体抗压强度测试值（表2）可知，混凝土7 d抗压强度随玄武岩纤维的增加呈现不变到逐渐降低的特征，这主要是由于玄武岩纤维加入后，在纤维与水泥形成的界面处产生一个薄弱面，而随着纤维掺量的增加，这类薄弱面不断增加，因此立方体抗压强度自然就会不断下降。而混凝土28 d抗压强度随玄武岩纤维掺量的增加呈现出先增加后降低的趋势，这个先增加的原因是少量掺入的玄武岩纤维起到了一定的连接作用，在一定程度上减少了混凝土自身的收缩变形，而同时增加的薄弱面相对28 d强度提高要少很多，从而在整体上表现为强度增加。

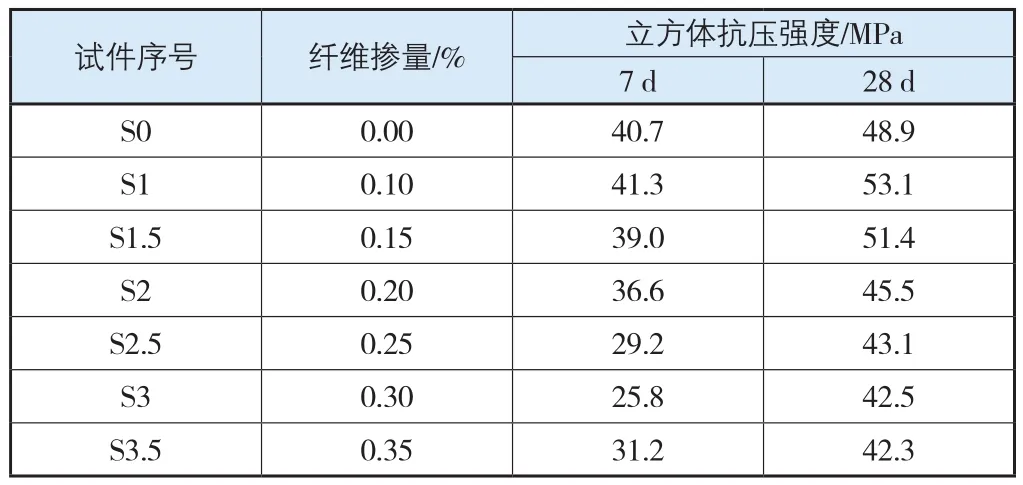
表2 立方体抗压强度测试值

由立方体劈拉强度测试值（表3）可知，基准混凝土的7 d立方体劈拉强度是28 d立方体劈拉强度的76.9%，随着短切玄武岩纤维不断掺入，7 d与28 d龄期的立方体劈拉强度差值开始减小，7 d强度均到达28 d强度的85%以上。根据前面数据，一方面掺入的纤维延缓了混凝土立方体抗压强度的增长，一方面掺入纤维对立方体劈拉强度而言并无太大的影响。

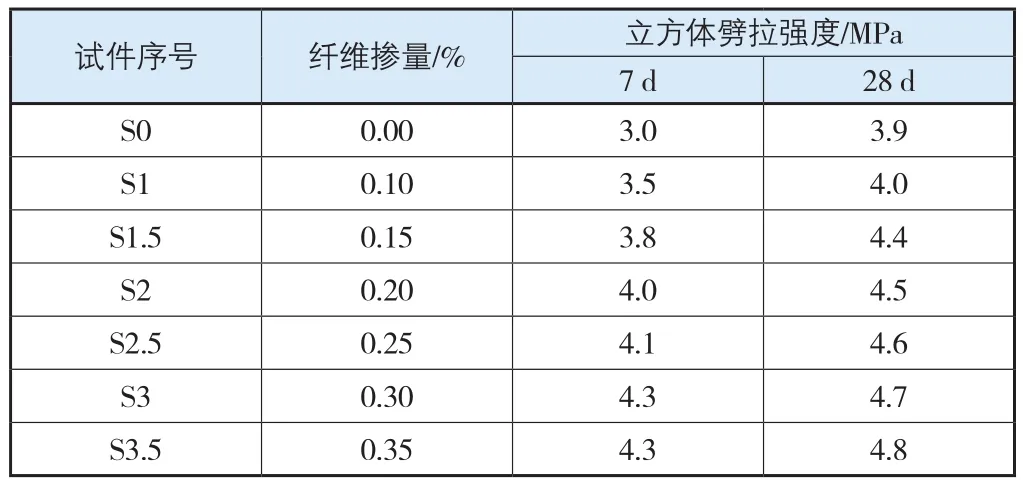
表3 立方体劈拉强度测试值

随着玄武岩纤维掺量的增加，短切玄武岩纤维混凝土的立方体劈拉强度有一定程度的提高：以普通混凝土为研究基础，当短切玄武岩纤维掺量为0.35%时，劈拉强度提高约23.1%。在加荷初期，纤维混凝土混合体刚度较大，变形相对较小，混凝土自身变形较小，因此混凝土承担大部分拉应力，而玄武岩纤维所承担的小部分拉应力也比较小。随着荷载的增加，混合体总变形开始增大，总应变也不断增加，此时，混凝土基体部分随着变形增加承担的拉应力也在增加，但是玄武岩纤维在这个过程中由于变形得更为充分，因而承载的拉应力增加很快，超过混凝土。显然，短切玄武岩纤维的加入减缓了混凝土基体由于张拉作用导致裂纹产生的速度，随着外力的不断施加，内部出现细小微裂纹，此时玄武岩纤维开始承担部分拉应力，促使应力进行重分布，这种拉接力使得裂纹处材料并未完全退出承载，进而继续承担一部分荷载，这样使得裂纹扩展得到了较好的约束。

6 工程应用

湖南省宁道（宁远县—道县）高速公路总路程约91 km，属于厦成高速湖南省段的重要组成部分。全线以黏性土和碎石土为主，局部分段为裸露基岩。基于前文相关研究，考虑到经济性，选用0.15%玄武岩纤维混凝土进行部分路段施工，后期对比观测掺入纤维和未掺入纤维混凝土的特征：掺入纤维段混凝土路面开裂情况明显优于未掺入纤维路段，掺入段仅有3处最长长度为6 m、最大宽度为1 mm的裂缝，裂缝在距离板切缝为3 m、1 m处，而未掺入段有8处最长长度为11m、最大宽度为2 mm的裂缝，且裂缝在距离板切缝约为0.5 m、1 m处。上述路面特征表明，玄武岩纤维混凝土对实际工程中减少裂缝的产生具有极其重要的意义。

7 结语

本文从理论和实际应用2个角度对玄武岩纤维混凝土进行了相关研究，得到如下结论：

1）从立方体抗压强度角度分析，当短切玄武岩纤维掺量达到体积百分比的0.10%～0.15%时，短切玄武岩纤维混凝土的7 d和28 d的立方体抗压强度较没有掺加纤维的混凝土均有一定幅度的提高。

2）掺入短切玄武岩纤维的混凝土立方体劈拉强度均有一定程度的提高。

3）在实际玄武岩纤维混凝土路面工程中，短切玄武岩纤维的应用能够明显减少路面裂缝的产生。