红外目标模拟仿真系统中定向镜的模型参考自适应控制与仿真

吴振远，郭艳颖

（广州民航职业技术学院 飞机维修工程学院，广州 广东 510000）

红外目标模拟仿真系统是研究和发展红外寻的制导武器的一项先进技术。它为红外寻的制导武器系统的研制提供了一种快速有效而又经济的手段。红外制导武器半实物仿真技术需要建立逼真的红外目标背景环境，制导装置支撑架，导弹空气动力学模型和作用于导弹舵面上的绞链力矩模型，而红外目标背景仿真装置是其中的关键，它在很大程度上决定着红外目标模拟仿真系统的逼真程度。为提高红外目标模拟仿真系统的仿真精度，采用目标二级定位决策进行控制系统设计，目标二级定位系统是由两轴的定向镜系统组成，所以定向镜伺服系统的精度将会直接影响红外目标模拟仿真装置的仿真精度。

1 定向镜系统的数学模型

定向镜系统是一个复杂的非线性、强耦合系统。定向镜系统的典型结构图如图1所示。

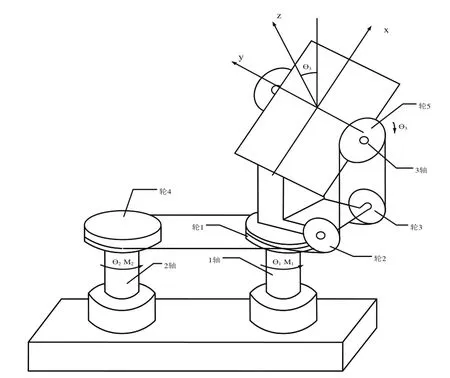
图1 定向镜系统结构图

图中：轴1为方位电机驱动轴；轴2为俯仰电机驱动轴；轴3为控制俯仰驱动轴；1轮为俯仰从动轮；2轮为俯仰支撑轮；3轮为俯仰支撑轮；4轮为俯仰电机驱动轮；5轮为俯仰角度驱动轮。

根据定向镜系统的机械结构，利用分析动力学方法，列写Lagrange方程，建立定向镜系统的数学模型，通过化简和线性化处理得到定向镜系统的简化数学模型为：

式中：J1、J2、J3是由定向镜的机械结构尺寸决定的常数，具有转动惯量的量纲和意义。

2 定向镜伺服系统典型频域方案设计

针对定向镜伺服系统的数学模型，采用方框图等效原理进行系统解耦。解耦后俯仰轴系统和方位轴系统可看成两个独立系统。再根据定向镜系统的技术指标确定系统结构、控制方案以及组成系统的元部件。定向镜系统的具体的技术指标要求如下：（1）方位轴旋转范围：±2º（34.8mrad）。（2）俯仰轴角速度不大于 150º/s；（2.61rad/s）。（3）俯仰轴旋转范围：±3º（53.3mrad）。（4）俯仰轴角加速度不大于600º/s2（10.4rad/s2）。（5）方位轴角加速度不大于400º/s2（6.99rad/s2）。（6）方位轴角速度不大于100º/s（1.76rad/s）。（7）误差不大于0.6mrad。定向镜系统的控制精度要求很高，对响应速度要求很快，所以对于定向镜的俯仰轴系统和方位轴系统均采用速度环和位置环的两重闭环结构。确定定向镜伺服系统的控制结构图如图2。

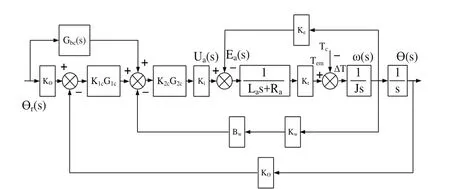
图2 定向镜系统控制结构图

由于定向镜系统要求有较大的加速度，速度变化快，对系统动态品质要求较高。因此，设计速度环是为了保证系统有高性能的动态响应以及降低系统的灵敏度、抑止噪声、限制电机速度等。为了将系统的稳态误差控制在允许范围内，可以采用串联积分环节，也可以采用提高系统开环增益的方法，但这些方法都有可能减小系统的相对稳定性，甚至会使系统不稳定。针对这个问题，可以采用给定量反馈和顺馈控制相结合的控制方案。利用顺馈控制在不影响系统稳定性的前提下提高系统的型别。位置环内采用串联滞后校正提高系统的增益，满足系统的带宽要求。系统设计后在MATLAB下进行仿真试验得到了闭环控制系统的位置环单位阶跃响应曲线，通过对仿真曲线的分析可以看到，控制系统的超调量为10%，调整时间为0.06s，满足了系统性能指标的要求。

3 模型参考自适应控制设计

当定向镜系统处于低速运行状态时，由于摩擦力矩的影响加大，常规反馈控制无法将系统误差控制在允许的稳态误差范围之内，因此，常规反馈控制无法满足系统低速跟踪精度的要求。本文采用模型参考自适应控制理论设计控制器，以达到减小摩擦力矩干扰影响，提高系统低速状态下运行稳定性的目标。位置环闭环阶跃响应曲线图如图3。

图3 位置环闭环阶跃响应曲线

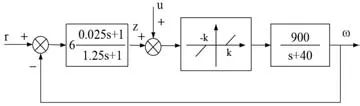
图4 速度环电机系统控制框图

控制系统的设计采用模型参考自适应控制方法，首先写出描述被控对象输入输出关系动态过程的微分方程：

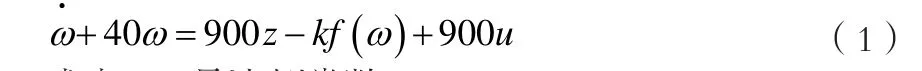
式中：k是比例常数。

选定的自适应参考模型的微分方程：

其中：mω表示参考模型的理想速度，将参考模型与被控对象的微分方程相减，可得速度偏差信号微分方程：

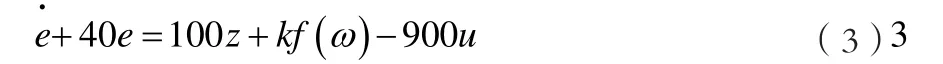
式中： e=ωm-ω。

为了减小被控对象的参数变化和非线性摩擦力矩的影响，利用能直接获取的输入信号z、输出信号ω来综合自适应控制信号u，因此，可令：

采用Lyapunov直接法来设计自适应律。选取能量函数V为：

其中：1α、2α、3α、1β、2β、3β为大于0的任意常数。对能量函数V求时间导数得：

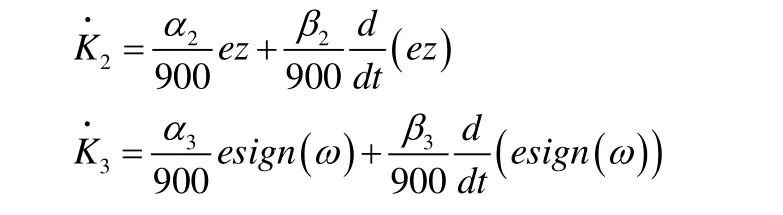
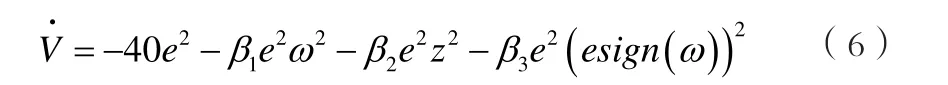
最后，可得自适应控制律：

取系统输入信号为斜坡速度信号 r(t)=0.01t时，通过MATLAB仿真，得出了有摩擦力矩情况下线性控制的误差曲线，和有摩擦力矩力矩情况下自适应控制的误差曲线。由图5可看到，摩擦力矩使得系统线性控制的输出信号有3s的死区现象，不能很好的跟踪输入信号，误差为0.0172。由图6可看到，由于摩擦力矩的作用，自适应控制的输出信号仅有0.5s死区现象，基本消除了死区，误差仅为0.000503。

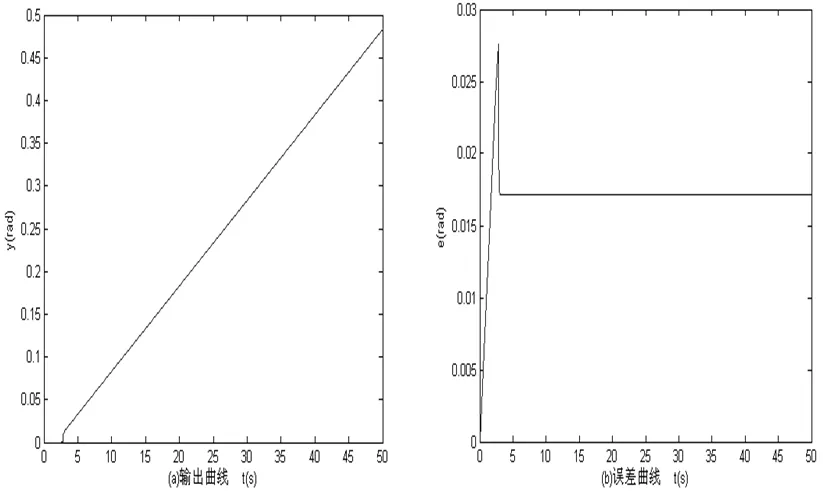
图5 有摩擦力矩线性控制仿真曲线

4 结语

定向镜伺服系统在低速运行状况下，采用模型参考自适应控制，有效的减小甚至消除了摩擦力矩干扰引起的死区现象，渐进跟踪参考模型输出信号，提高了系统低速运行性能，增强了系统鲁棒性，体现了模型参考自适应控制的优越性。

图6 有摩擦力矩自适应控制仿真曲线

图5 为有摩擦力矩线性控制仿真曲线图。

图6为有摩擦力矩自适应控制仿真曲线图。