近海潮汐效应对上海地区精密定位的影响
丁倩云,孙宪坤,尹玲,郝美云,尹京苑
(1.上海工程技术大学,上海 200000;2.上海市地震局,上海 200000)
0 引 言
由于受到日月的引力,海水会产生周期性的涨落,该现象称为海洋潮汐,潮汐使得海水质量重新分布,固体地球对此产生的弹性响应称为海潮负荷效应(OTL)[1]。根据Farrell理论[2],海潮负荷位移可由全球海潮模型和格林函数的褶积分计算得出,因此,全球海潮模型建立方式以及精度不同会造成海潮负荷位移的差异[3-5]。文献[3]采用三种不用的海潮模型分析海潮负荷对山东区域GPS定位的影响,得出利用NAO99b海潮模型计算得到的山东CORS站垂直方向位移最大达到了28 mm,相比FES2004和CSR4.0海潮模型,NAO99b更适用于山东地区海潮负荷改正。文献[4]选取江苏近海测站和西安内陆GPS测站,利用NAO99b以及FES2004两种海潮模型计算海潮负荷的影响,结果表明两种海潮模型在内陆差异很小,在沿海区域差异达1 cm以上。
近年来较新的全球海潮模型大多数都是通过卫星测高技术以及流体动力学理论建立[1],而中国近海区域特殊的海岸线、复杂的海底地形导致了全球海潮模型在近海区域精度较差[6-10]。用验潮站观测资料建立的中国近海海潮模型,能更好地反映中国近海区域海洋潮汐变化[7-8]。文献[9]将中国东海和南海的近海海潮模型和HAMTIDE11A.2011全球模型相结合,计算了海潮负荷对不同地区GPS测站的影响,结果表明,修正前后,海潮负荷对GPS测站定位的影响存在5 mm的差异。文献[10]利用TPX06全球模型与中国东海和南海潮汐资料分析了近海潮汐效应对沿海部分测站的影响,结果表明,在沿海GPS测站的影响最大达到了15 mm.上述研究表明,全球海潮模型在中国近海区域精度不高,需要利用中国近海模型进行修正。
上海地区作为沿海发达城市,对GPS精密定位的要求越来越高,海潮负荷作为影响GPS精密的一个重要影响因素,尤其是对沿海城市影响更是显著,因此分析海潮负荷对上海地区GPS精密定位的影响是必要的。针对上述分析得出的全球海潮模型在不同沿海地区存在差异性以及全球海潮模型精度不高的问题,分析NAO99b、FES2004两种全球海潮模型在上海地区的差异性。然后利用中国东海、南海海潮模型osu.chinasea.2010对全球海潮模型进行修正,对比修正前后模型计算得到的海潮负荷对上海GPS精密定位的影响。
1 海潮负荷计算原理
海潮负荷对测站位移影响可以表示为海潮潮高和格林函数的褶积积分:
G(φ,A)sinφdφdA,
(1)
式中:ρw为海水密度;R为地球半径; (θ,λ)为测站的球坐标; (θ′,λ′)为负荷点的球坐标;φ和A分别是测站到负荷点的球面角和方位角;H(θ′,λ′,t)为(θ′,λ′)处的瞬时潮高;SG为整个海面;L(θ,λ,t)为在t时刻U、W、S分量的海潮负荷;G(φ,A)为位移负荷格林函数和方位角的组合。
由于近海区域海岸线特殊、海底地形复杂,全球海潮模型在近海区域精度有限,为了进一步提高精度,可利用高精度的近海海潮模型替换全球海潮模型中对应的区域,此时,海潮负荷的计算公式为:
(2)
式中:SL表示近海区域;HL(θ′,λ′,t)表示近海区域的舒适潮高;L′(θ,λ,t)为修正全球海潮模型后的海潮负荷。
因此,由公式(1)和公式(2)可以得到近海效应:
δL=L′(θ,λ,t)-L(θ,λ,t) .
(3)
通过积分得到测站位移的海潮负荷影响后,通过在频域求得各分潮波位移改正的振幅和相位后,总的海潮负荷效应就是不同潮波的叠加:
(4)
式中: Δc为在t时刻测站垂直方向、东西方向和南北方向的位移;i为分潮波总数;fi为与月球升交点经度有关的系数;Acj、φcj分别表示测站第c个位移分量相对应的第j个分潮波的振幅和格林尼治相位;wj、χj分别为第j个分潮波的角频率和天文幅角;fj、μj为与月球升交点经度有关的系数和参数。
2 实例分析
2.1 区域选取
选取经纬度范围为120°E~122.5°E,30.5°N~32°N,其中上海地区经纬度范围为120.85°E~122.2°E,30.6667°N~31.8833°N,并选取上海地区四个GPS测站SHJS站(上海金山)、SHBS站(上海宝山)、SHAO站(上海佘山)和DCMD站(上海崇明)作为研究对象,分析海潮负荷对上海地区的影响。区域站点分布如图1所示。
2.2 全球海潮模型FES2004和NAO99b在上海地区的差异分析
为了分析不同海潮模型在上海地区差异,采用FES2004和NAO99b两种全球海潮模型,利用SPOTL软件分别计算所选区域0.5°×0.5°的海潮负荷位移振幅大小。根据文献[14]和[15]分析,在中国东中国海基本以半日潮(S2,M2)为主,其中M2占优,而南海以全日潮为主,以K1和O1为主。因此分析两个全球模型计算的S2、M2、K1和O1四个潮波的海潮负荷位移在垂直分量上的差异如图2~图5所示。
从图中可以看出,FES2004和NAO99b海潮模型计算得出的M2、S2两个半日潮垂直分量的海潮负荷位移的振幅在离海域较远的区域(120°E~120.5°E)的差异都小于1.5 mm,K1、O1两个全日潮的差异都小于0.5 mm,说明这两个全球海潮模型在我国中部地区K1、O1两个全日潮的精度相当。对于上海地区中较靠近东海海域的区域(如宝山、崇明),M2分潮垂向分量的海潮负荷位移的振幅的差异达到2.8 mm的最大值,S2分潮的差异达到3.9 mm的最大值,K1分潮的差异最大为1.8 mm,O1分潮的差异最大为1.2 mm,且越靠近东海海域,海潮负荷位移差异越大。从这四个分潮的垂直分量海潮负荷位移的振幅差异的趋势可以看出,海潮负荷位移随着离海洋距离增大而减小。水平方向的东西分量和南北分量具有相同的走势,但差异是大约垂直分量的三分之一,表明海潮负荷主要影响垂直分量。通过上述分析,FES2004和NAO99b海潮模型在内陆地区精度相当,但在上海地区相差较大,这是由于两者模型数据获取方式、分辨率不同。
2.3 经中国近海模型修正前后的FES2004海潮模型对上海测站位移的影响分析
表1示出了FES2004、NAO99b两个全球海潮模型和osu.chinasea.2010中国近海模型的基本信息。相对于NAO99b海潮模型的构建方法和分辨率,FES2004海潮模型是有限元海潮模型中的最新版本,并且同化了T/P卫星测高数据、ERS-2交叉点数据和验潮站数据[6],并且具有更高的空间分辨率。osu.chinasea.2010海潮模型是基于流体动力学模型同化T/P卫星测高数据构建的中国近海海潮模型,覆盖范围为1°E~41°E,98°N~129°N。因此选择用osu.chinasea.2010中国近海模型修正FES2004全球海潮中的相应区域,计算修正前后的海潮负荷对SHJS、SHBS、SHAO以DCMD.
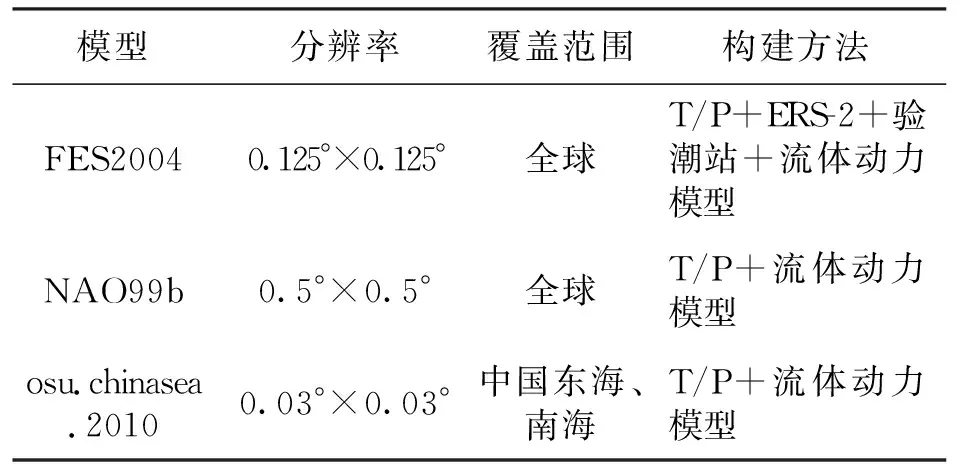
表1 近海模型及全球海潮模型
利用SPOTL软件计算修正前后上海四个GPS测站的8个分潮的振幅和相位,根据公式(4)得到2014年091天到118天共28天海潮负荷对上海GPS测站E、N、U三个分量的位移的时间序列,如图6所示。
由图6可以看出,对于SHJS、SHBS和DCMD,修正前后的全球海潮模型计算的海潮负荷在两个水平分量的差异分别为1.4 mm、1.1 mm、1.3 mm,在南北分量的差异均为1 mm,在垂直分量的差异为4.2 mm、4.9 mm,5 mm;对于距海洋较远的佘山站SHAO,在东西分量差异为1.1 mm,在南北分量的差异小于1 mm,垂直分量的差异达3.6 mm.通过上述分析可知,修正前后的全球海潮模型计算的海潮负荷主要影响上海GPS测站的垂向分量,并且对临海测站SHJS、SHBS、DCMD的影响较大,可以分析得出海潮负荷的影响随测站距离海洋增大而减小。修正前后的全球海潮模型对上海测站海潮负荷的计算差异较大,进一步说明了全球海潮模型在中国近海区域精度不高。
2.4 近海效应对上海GPS测站的影响
利用公式(3)可以计算近海效应测站的影响,近海效应指修正前后的全球海潮模型的差异[4],能够反应近海造成的海潮负荷影响。本文用修正前和修正后的FES2004全球海潮模型计算海潮负荷对上海四个GPS测站的影响,主要分析四个主要潮波S2、M2、K1和O1的近海效应在E、N、U三个方向的振幅,如表2所示。
由表2可以看出,S2和M2两个分潮的近海效应对上海四个GPS测站的水平位移的影响都小于0.5 mm,都在亚毫米级,对测站垂直方向位移的影响都在毫米级,其中SHBS站(上海宝山)和DCMD站(上海崇明)垂直分量位移较大,达到1.9 mm,可能是因为两个测站距离海域较近,以及崇明岛特殊的地形导致。K1、O1两个分潮的近海效应对上海GPS测站水平和垂直方向位移影响都不大,都小于0.2 mm。这说明全球海潮模型在上海地区精度不高,尤其是对于较临海的测站,所以需要利用近海模型修正全球海潮模型以分析海潮负荷的影响。

表2 近海效应对测站的负荷影响单位:mm
进一步分析近海效应对上海测站位移的总影响,利用8个潮波计算了四个测站垂直分量的海潮负荷位移,如图7所示,计算时间为2014年091—118共28天。由图7可知,虽然上海四个测站的地理位置不同,但近海效应对四个测站垂直分量的位移影响相差不大,都接近5 mm,其中上海崇明站影响最大,超过5 mm,通过测站分布图可知,上海崇明四周环海,且地形构造特殊,由泥沙堆积而成,所以近海效应对DCMD站的影响略大。
3 结束语
利用SPOTL分析了全球海潮模型FES2004和NAO99b在上海地区经纬度范围为120.85°E~122.2°E,30.6667°N~31.8833°N的差异,并利用中国近海模型修正全球海潮模型FES2004,分析近海效应对上海地区GPS测站精密定位的影响。经过实验分析得出,1) 全球海潮模型FES2004和NAO99b在内陆地区精度相当,但在上海地区计算的海潮负荷差异较大,且精度不高,需要利用近海模型加以修正;2) 经过修正后的FES2004模型对上海地区测站位移影响显著,水平分量最大达到1.4 mm,垂直分量最大达到5 mm,并且海潮负荷对上海宝山、金山、佘山、崇明四个测站的影响随测站离海洋距离增大而减小,但差异不大,说明海潮负荷对上海地区的影响几乎一致;3) 近海效应对测站位移垂直分量位移的影响达到5 mm,因此在上海地区进行高精度GPS观测时必须考虑近海效应的影响。

