基于直连BP神经网络模型的森林火险预测

王亚琴，王耀力，郭学斌，孙永明

（1.太原理工大学信息工程学院，山西 晋中 030600；2.山西省林业科学研究院，山西 太原 030000）

由于受气候条件、地理条件和人为因素等多种不同因素的影响，森林火险的发生具有很大的波动性，其中，气象因素是森林火险发生的主要诱导因素[1-4]。很多学者对气象因子与森林火险之间的关系进行了研究，并利用传统的统计学方法建立了气象因子与森林火险之间的预测模型[5-10]。谢克勇等[5]分析了日照时数、气温、相对湿度及降水与森林火险之间的关系，得出森林火险与日照时数呈正相关，与相对湿度和降水成负相关，与气温密切相关，为科学预防森林火险提供了参考。徐海龙[6]运用主成分分析和聚类分析方法建立了林火过火面积预测模型。李丽琴[7]通过统计学方法分析得出风速、气温年较差、平均气温与森林火灾的发生有显著相关性。李德[8]探究了四川省近30年森林火灾重灾区火灾发生与气象因子的关系，得出重灾区森林火灾与风速、日照时数、降水量呈显著线性相关。王智慧等[9]建立了气象因素与森林火险的回归模型，结果表明年平均相对湿度对森林面积与森林火险存在显著影响，并建立了线性回归模型进行拟合。苏漳文[10]将福建省2000年至2004年的林火数据作为训练样本，2005年的林火数据作为测试样本，结果表明日最高地表温度、最低地表温度、平均风速、日照时间、平均相对湿度等9个变量与林火发生显著相关。

近年来，基于气象因子建立神经网络森林火险预测模型成了研究热点[11-18]。例如：杨景标[13]以气象因子作为网络输入，以广东省林火发生与否、次数和林火面积等作为输出，建立了人工神经网络预测模型，获得了较好的预测效果。王丹丹[14]以河南登封地区的气象条件为基础，采用BP神经网络建立了森林火险发生预测模型，建模精度为0.97，取得了较好的拟合效果。Safi等[15]讨论了基于神经网络的森林火灾预测模型，并以葡萄牙Montesinho自然公园相关的真实测试数据为例对该模型进行了仿真，获得了较为满意的结果。马奔等[16]以1997—2012年的全国森林火灾成灾面积为依据，应用BP神经网络模型对成灾面积进行了预测，然后利用残差提出了修正的BP神经网络模型，并对改进的模型进行了预测。

BP神经网络能够很好地拟合输入与输出之间复杂的非线性关系。文献[7-9]通过气象因子与森林火险的相关性分析，得出它们之间存在着显著的线性相关性，因此，气象因子和森林火险之间既存在复杂的非线性关系，也存在一定的线性关系，所以采用BP神经网络很难描述出它们之间复杂的关系。因此，本文提出一种改进的网络—直连BP神经网络（BPNN-DIOC）用于构建森林火险预测模型。为了探究该网络的有效性，根据是否存在输出层阈值和输入到输出之间的连接而扩展了4个不同的森林火险预测模型，并对网络进行训练，最后进行网络泛化能力的测试。

1 改进神经网络描述

1.1 改进思路

人工神经网络(Artificial neural networks,ANN)可以被描述为将第m个输入向量X（m）映射到第n个输出向量O（n）的函数。函数的形式，即输入和输出之间的函数关系决定了网络拓扑结构，可以近似表述为[19]：①输入变量的线性函数，对应没有隐含层的单层感知机网络，这种结构产生的预测误差非常大，不适合用于预测；②输入变量的非线性函数，对应具有非线性拟合特性的BP神经网络，其网络结构如图1所示；③输入变量的线性和非线性组合函数，对应基于BPNN加入输入到输出连接的BPNN-DIOC，其网络拓扑结构如图2所示。

从图1和图2可以看出，BPNN-DIOC的网络拓扑结构与BPNN相似，主要区别在于BPNN-DI⁃OC加入了从输入到输出的直接连接。1991年，Peng等[19]提出了一种改进的BP神经网络算法，该算法在常规BP神经网络中加入了输入层到输出层的连接，形成具有线性和非线性模型结合的网络，并用于短期电力负荷预测，预测精确度提高了1%。2016年，Ren和Suganthan[20]通过采用澳大利亚能源管理运营商（Australian Energy Market Op⁃erator,AEMO）新南威尔士州的电力负荷数据对RVFL（Random Vector Functional-Link）网络进行了全面的评估。结果表明从输入到输出的连接在网络性能中起着非常重要的作用，使网络在具有高度非线性映射能力的同时又具有了从输入到输出的线性映射能力，从而可以更准确的表示出输入与输出之间完整的映射关系。可以看出，这种网络结构具有一定的优势。

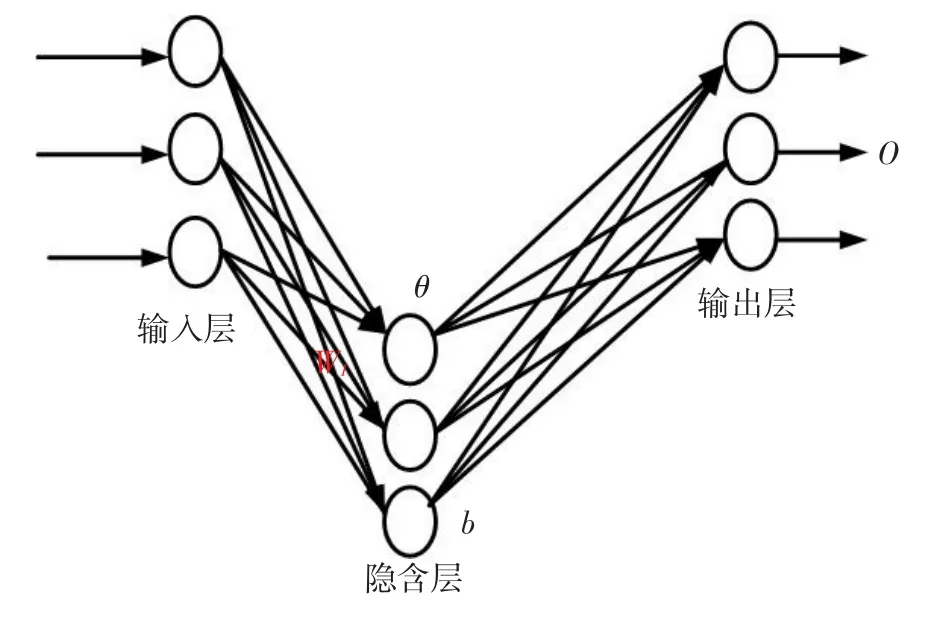
图1 神经网络拓扑结构

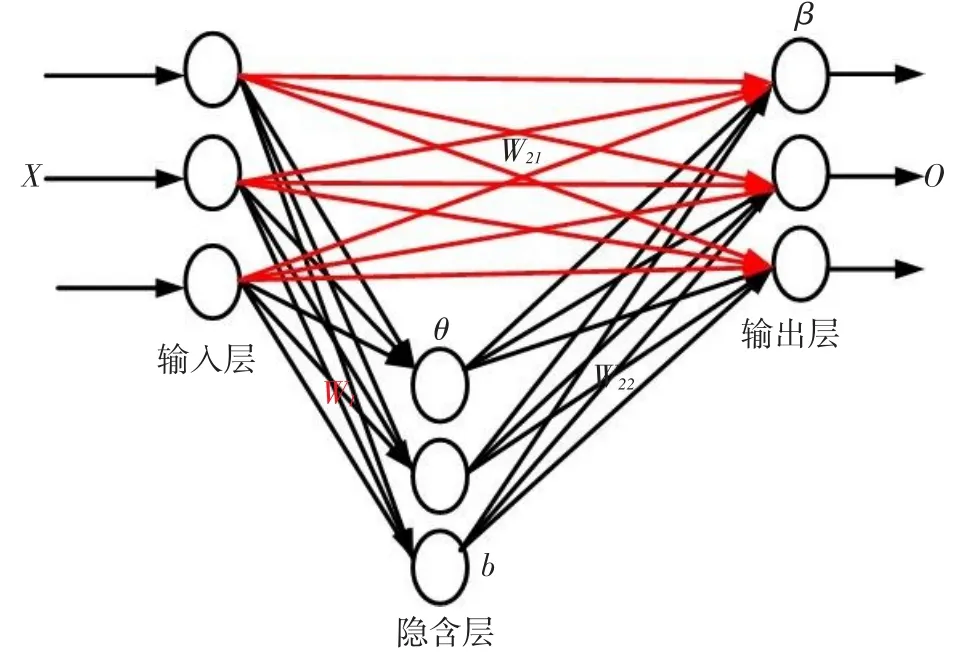
图2 直连BP网络拓扑结构

目前，该网络模型还没有应用在森林火险预测上。因此，本文以太原和桂林两个地区的森林火险情况为例（表1），首先，分析气象因子与森林火险之间的相关性；然后，从BP神经网络角度出发，根据是否存在输出层阈值和输入到输出之间的连接而扩展了4个不同的森林火险预测模型，并分别进行训练；最后，对网络的泛化能力进行测试。

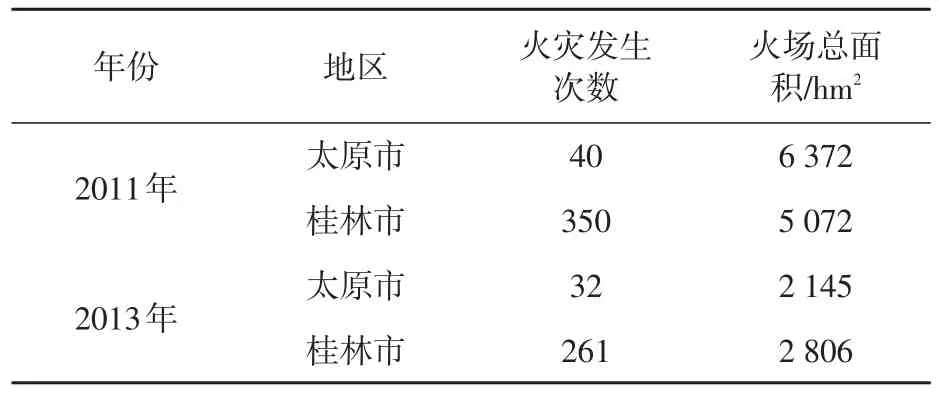
表1 太原市和桂林市的火灾情况

1.2 数据分析

1.2.1 自然概况

太原市位于东经111°30′～113°09′，北纬37°27′～38°25′之间，属于北温带大陆性气候。年平均气温9.5℃，冬季室外相对湿度是46%，夏季相对湿度是51%，年平均风速为9 km/h，年均降水量456 mm。总特征为：春季干燥多风，夏季炎热多雨，秋季天高气爽，冬季寒冷少雪。其中在3、4、5三个月，大部分地区气温较高、空气干燥、风力也较大，很容易发生火灾，是太原市森林火险发生的高频月份，发生的火险占全年的80%以上。

桂林市位于东经109°36′～111°29′、北纬24°15′～26°23′，属于亚热带季风气候。年平均气温19.3℃，年平均相对湿度是73%，年平均风速为0.6～0.75 km/h，年均降水量1949.5 mm，十分有利于多种林木的生长和林业的发展。桂林森林资源丰富，2016年森林覆盖率达70.91%，植被种类繁多，有包括银杉、红豆杉、银杏在内的高等植物1000多种。因此，要谨防森林火险的发生。

每个不同的地区都有不同的气候条件。从表1可以看出，桂林属于森林火险发生较频繁的地区，但是太原地区风力较大，因此造成火势蔓延快，火场面积较大。

1.2.2 气象因子和森林火险的相关性分析

众所周知，森林火灾的起火、传播等过程与气象条件密切相关，而引起火灾的主要气象因子有温度、相对湿度、风速和降水量。本文选取太原市2011年5月1日-31日、2013年5月10日-22日，桂林市2005年6月1日-30日、2010年6月1日-13日的气象数据和森林火险记录作为研究对象。为了探讨这4个气象因子与森林火险之间的关系，我们建立了气象因子与森林火险之间的回归模型[9]。

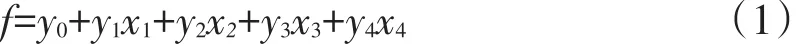
其中，x1为日平均温度，x2日平均相对湿度，x3为日平均风速，x4为日平均降雨量。f表示森林火险是否发生，1是林火发生，0是不发生。

对于太原地区，该回归方程F检验的值为6.1798，对应的P值为5.96×10-4；对于桂林地区，该回归方程F检验的值为17.7902，对应的P值为2.63×10-8。很显然，两个地区样本的F检验的P值均小于0.05，这意味着在显著性水平为0.05时，4个气象因子对森林火险的联合线性影响是显著的，即气象因子和森林火险之间既存在复杂的非线性关系，也存在一定的线性关系。

表2为两个地区的4个气象因子与森林火险的相关性分析。从表中可以看出，对于太原地区，温度与森林火险之间存在着显著的正相关性，表明温度越高，火险发生的概率越大；对于桂林地区，相对湿度与森林火险之间存在着显著的负相关性，表明相对湿度越低，发生林火的概率越大。这和当地的气象条件有很大的关系。表2的分析结果说明，在总体5%显著性水平下并不是所有影响因子都与森林火险存在显著的相关性，这可能是由于因子间相互的影响作用使得某些因子对因变量的影响被其他因子的影响关系覆盖了。

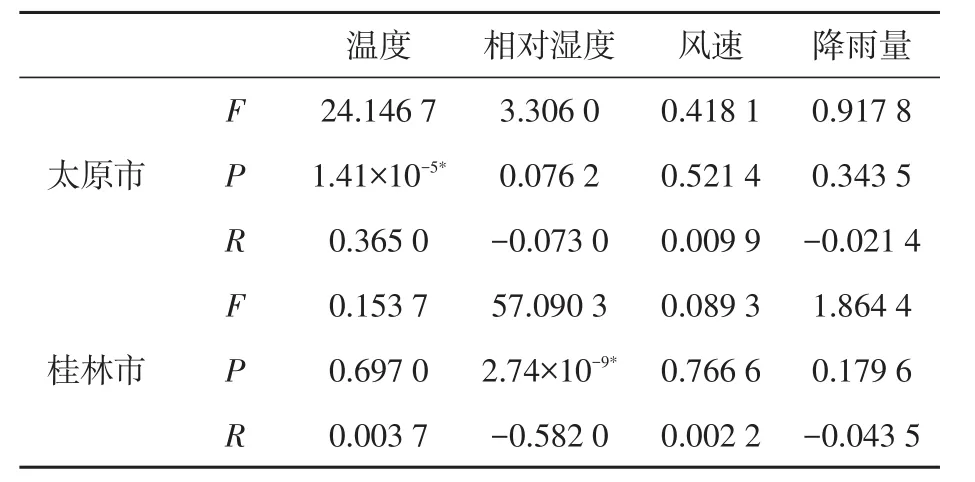
表2 气象因子与森林火险的相关分析

2 实验设置

2.1 BP神经网络的扩展

根据从输入层到输出层是否有连接和输出层是否有阈值，可以将BP神经网络扩展成4个不同的神经网络模型，见表3。

表3 4种不同的神经网络模型

2.2 构建神经网络森林火险预测模型

本文选取日平均气温、日平均相对湿度、日平均风速和日均降水量作为神经网络的输入，森林火险是否发生作为输出，其中1表示发生，0表示不发生。隐含层神经元的个数对神经网络预测模型的学习能力有很大的影响，直接影响其预测结果。本文采用五折交叉验证法选取合适的隐层神经元个数S，通过找出样本在不同的隐层神经元个数中最小的误差，从而得到最佳的隐含层神经元个数，构建最优的神经网络预测模型。

2.3 预测精度分析

为了对4种神经网络的预测精度进行分析，本文采用均方根误差（RMSE）来衡量网络的预测能力，RMSE越小，网络的预测性能越好。它的定义为：

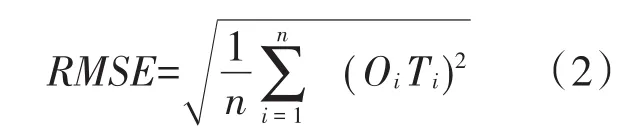
式中，n为数据的长度，Ti代表实际的目标值，Oi是网络输出反归一化后的值。

2.4 仿真结果及分析

本文选取太原市2011年5月1-31日，桂林市2005年6月1-30日的气象数据和森林火险记录作为训练样本，2013年5月10-22日和2010年6月1-13日的数据作为两个地区的测试样本。仿真平台为MATLAB R2012a，对训练样本分别构建4种神经网络森林火险预测模型，之后对测试样本进行拟合，试验重复10次。

2.4.1 最佳隐层神经元数比较

表4为4种网络所需的最佳隐层神经元数。通过比较M1、M3以及M2、M4可以看出，从输入到输出的连接是否存在对选取最佳隐含层节点个数有很大的影响，没有输入到输出直接连接的网络（M1，M2）比具有输入到输出直接连接的网络（M3，M4）需要的隐含层神经元数要多。而通过比较M1、M2以及M3、M4可以看出，输出层阈值是否存在对网络选取最佳隐含层节点个数几乎没有影响。

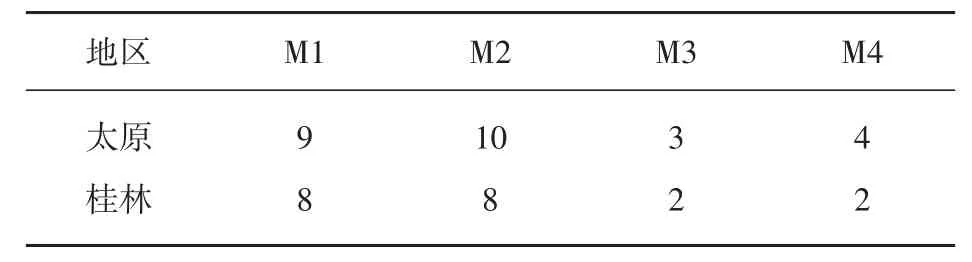
表4 4个网络所需的最佳隐层神经元数

2.4.2 预测结果比较

表5列出了4种不同网络模型重复10次试验的平均RMSE及标准差。仿真结果表明，直连BP神经网络模型可以获得比BP神经网络模型更高的预测精度，并且该方法不仅对森林火险发生较频繁的地区有效，对森林火险发生较少地区也有很好的预测效果，具有良好的通用性。

Two-sided Wilcoxon signed rank test是非参数的统计假设检验，用于比较两个样本之间是否存在显著的差别。P＜0.05时表示两个样本存在显著差异，而P＞0.05时表示两个样本之间无显著差异。为了比较BP神经网络模型中有无输出层阈值对网络预测性能的影响，对M1、M2以及M3、M4分别采用Two-sided Wilcoxon signed rank test测试，结果如表6所示。可以看出，预测结果之间没有显著的差异。因此，输出层阈值的有无不会影响网络模型的预测性能。

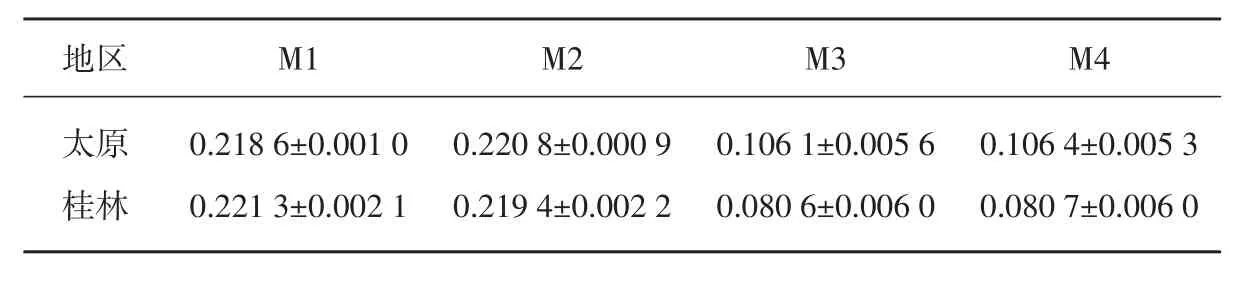
表5 4种不同预测模型的RMSE及标准差

通过对M1、M3以及M2、M4模型采用Twosided Wilcoxon signed rank test测试，以判断在BP神经网络基础上是否存在输入到输出的连接对网络模型预测性能的影响，结果如表7所示，可以看出预测结果之间存在着显著的差异，即在BP神经网络模型基础上加入从输入到输出的连接，即直连BP神经网络模型可以明显改善预测性能。

可见，在BP神经网络中加入从输入到输出的连接相当于网络具有了从输入到输出的线性映射能力，可以将气象因子对森林火险的影响更好的映射到网络的输出，从而更准确的用于森林火险的预测。

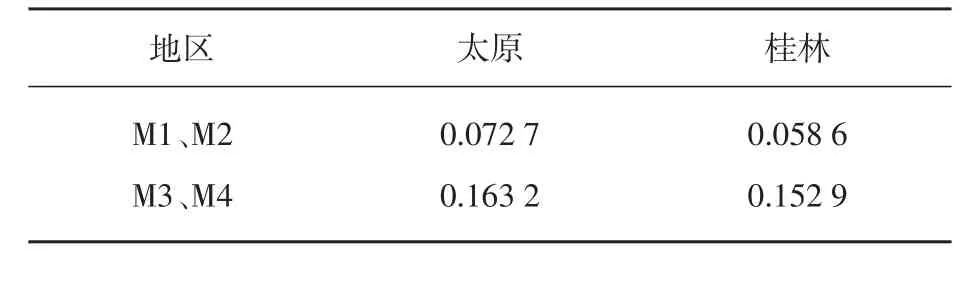
表6 有无输出层阈值的显著性比较

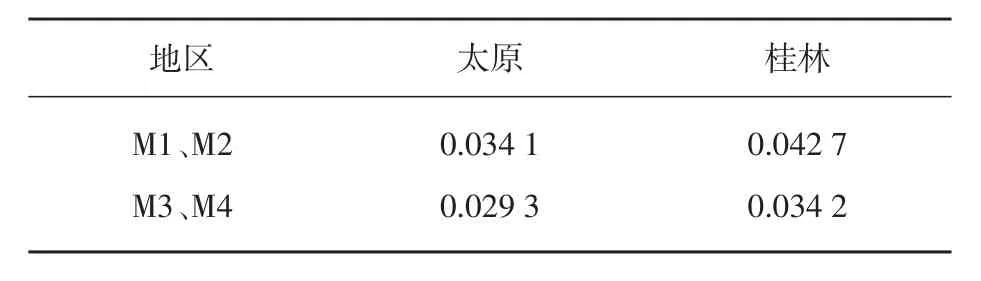
表7 有无输入到输出的连接的显著性比较

3 结论

通过4个气象因子与森林火险的相关性分析，得出气象因子与森林火险之间不仅存在复杂的非线性关系，还具有显著的联合线性特性。对于太原地区，温度与森林火险之间存在着显著的正相关；而对于桂林地区，相对湿度与森林火险之间存在着显著的负相关性。本文在BP神经网络的基础上根据是否存在从输入层到输出层的连接和输出层阈值，构建了4个不同的神经网络模型，由仿真结果可以得出以下结论：

1）BP神经网络模型中有无输出层阈值对网络所需的隐含层节点个数和预测性能几乎没有影响。

2）在BP神经网络上加入从输入层到输出层的连接可以大大减少所需的隐含层节点个数，降低网络所需调整的参数个数，加快网络的训练速度。

3）直连BP神经网络模型可以提高网络的预测精度，增强网络的泛化能力。因为在BP神经网络中加入从输入到输出的连接相当于网络具有了从输入到输出的线性映射能力，改善了具有高度非线性拟合能力的BP神经网络在处理非线性和线性综合问题方面的能力，可以更准确地将输入完整的映射到网络的输出。

4）基于直连BP神经网络模型的森林火险预测模型不仅适用于火灾发生频繁的地区，也适用于火灾发生较少的地区，具有很好的通用性。