岩体特性参数对坝基及近坝山体抬升变形影响研究

曾杨晨，李双龙，王 鹏，谭文帅

(1.江西省南昌县象湖联圩管理站，江西 南昌 330200；2.长沙理工大学水利工程学院，湖南 长沙 410076；3.湖南省株洲市佳联建设工程有限公司，湖南 株洲 410004)

0 引 言

坝基及近坝山体抬升变形现象在国内外相对少见。国外的托克托古尔重力坝[1]、英古里重力坝[2]在蓄水后都发现水工结构物有抬升变形现象；我国湖南省江垭大坝近坝山体最大抬升位移达21.8 mm[3，4]，铜街子水电站坝体右岸山体表面产生24.3～28.9 mm抬升位移[5]，金沙江向家坝左岸近坝山体抬升量超过13.0 mm[6]等。针对以上抬升变形问题，国内外学者进行了研究。Xiaoli Liu[7]等认为铜街子大坝及右岸近坝山体抬升变形的主要原因是分布在坝址区承压含水层作用和坝基强度参数的弱化以及构造应力的组合影响；王兰生[8]等利用MTS刚性压力试验机对岩体扩容行为进行试验模拟，认为承压含水层D2y内的孔隙水压力增高是造成坝基和近坝山体抬升的主要原因；伍法权[9]等结合监测数据与江垭水库地质资料，认为热水含水层中的有效应力减小，导致岩体卸荷扩容；祁生文[10]等利用FLAC3D数值软件对江垭大坝进行了抬升变形过程模拟，认为水库蓄水是抬升变形的本质原因。Fuzhang Yan[11]等通过三维数值模拟，得到了抬升变形的空间位移分布；蒋中明等[6]提出了水库蓄水条件下的抬升变形水文地质结构模式，探讨了不同坝基地质条件对抬升变形的影响。

由此可见，针对坝基及近坝山体抬升变形问题，现有成果侧重于外因研究，即抬升变形的本质原因在于水库蓄水，同时结合一定的特殊地质条件导致岩体有效应力降低，使岩体产生扩容变形，然而在抬升变形的内因条件方面研究不足，如岩体参数、水文地质条件等。本文拟基于应力场-渗流场耦合理论，充分考虑蓄水条件下渗透力作用，采用三维数值模拟方法，研究坝基及近坝山体中岩体变形模量及渗透系数对抬升变形的影响规律，进一步揭示抬升变形的变形机制。

1 抬升变形数值理论

1.1 流固耦合基本方程

根据文献[6]、[9]、[10]，水库抬升变形的诱因是水库蓄水，蓄水条件下坝基岩体在巨大渗透力作用下产生上抬变形，采用岩土数值软件FLAC3D可以实现对抬升变形过程的模拟。本文拟基于应力场-渗流场耦合理论，利用FLAC3D内嵌fish语言[12]，模拟坝基及近坝山体不同岩体参数在蓄水条件下的抬升过程。FLAC3D在模拟岩土体流固耦合问题中，将岩土体都作为孔隙介质来考虑，符合Darcy[13]定律，满足Biot[14]方程。下面给出FLAC3D计算采用的流固耦合基本方程。

(1)平衡方程

假定小变形条件下，流体质点平衡方程为：

-qi，j+qv=∂ζ/∂t

(1)

式中：qi为渗流速度，m/s；qv为流体源强度，1/s；ζ为单位体积流体体积变化量；t为时间，s。又有：

∂ζ/∂t=(1/M)×∂p/∂t+α(∂ε/∂t)-β(∂T/∂t)

(2)

式中：M为Biot模量，N/m2；p为孔隙水压力，Pa；α为Biot系数；ε为体积应变；β为热膨胀系数(1/℃)；T为温度，℃。此方程考虑了流固耦合作用中的温度效应，在本文研究中并没有考虑地下水温度的影响，故本文计算方程温度项可删除。

(2)运动方程

假定介质为均质、各向同性且密度不变，利用Darcy定律描述运动方程为：

qi=-k[p-ρfxjgj]

(3)

式中：k为介质渗透系数，m2/Pa·s；ρf为流体密度，kg/m3；gi，(i=1，3)为重力加速度的三个分量，m/s2。

(3)本构方程

流固耦合作用下，应力通过改变孔隙介质渗透属性来影响渗流场，渗流场的改变导致渗透力对应力场的改变，致使发生体积应变，其本构方程为：

Δσij～+αΔp=Hij*(σij，Δεij)

(4)

式中：Δσij～为应力增量；Hij*为给定函数；εij为总应变。

(4)相容方程

还需满足相容方程，即：

εij*=(vi，j+vj，i)/2

(5)

式中：vi，j为介质中某点的速度，m/s。

(5)连续性方程

联立平衡方程(2)和本构方程(4)可得到流体的连续性方程：

(1/M)(∂p/∂t)+(n/s)(∂s/∂t)=(1/s)(-qi，j+qv)-α(∂ε/∂t)

(6)

式中：s为节点饱和度，n为节点孔隙率，其他变量同前。

1.2 流固耦合数值实现

在FLAC3D数值计算中，将模型区域划分为四面体，将孔隙水压力和饱和度作为节点变量，依赖于流体连续性方程的有限差分节点表达式，以力学平衡作为起始状态，通过若干流体步及力学步相互转换循环计算，达到系统计算平衡；通过流体步得出孔隙水压力增量，力学步得出体积应变[12]。从而计算出计算模型整体渗流场及应力应变场分布。

2 数值模型

坝基及近坝山体的抬升变形现象实质为岩土体的扩容行为。影响此种扩容行为的因素诸多，除现有研究成果[6～11]提到的外因(水库蓄水导致坝基及近坝山体岩层渗流场变化而产生垂直向上的渗透力分量)及内因(坝址区特定的水文地质结构模式)之外，还存在诸如土体力学及水力学参数、坝址区岩层地下水温度以及坝体接触空气温度等其他可能影响因素，这些因素都将可能引起坝体及近坝山体不同程度的抬升变形。

依据应力场与渗流场耦合作用理论可知，坝基岩层渗透系数的改变，将引起坝基岩层整体渗流场的改变，进而改变应力场，产生相应变形。水库蓄水，岩层孔隙(裂隙)充水，孔隙(裂隙)水压力增大，有效应力降低，由此产生回弹扩容变形。因此，可初步认为：岩土体变形模量影响扩容变形的大小，而渗透系数的大小对流固耦合作用效应会产生不同程度的影响，进而影响抬升变形。

为验证以上观点，进一步揭示内因对抬升变形的影响，本文对坝基岩层变形模量及渗透系数对抬升变形的作用效应展开研究，进一步深入探讨抬升变形的形成机制以及变形规律，获得水库蓄水作用下库区抬升变形的位移空间分布规律。以下对坝基及近坝山体的抬升变形进行三维数值分析，分别研究不同岩体变形模量、不同渗透系数对水库枢纽区抬升位移分布的影响规律。

2.1 计算模型

由于实际坝址区岩层分布复杂，坝基及近坝山体岩层的岩体参数分布差异较大。根据蒋中明等[6]的研究成果，坝基及近坝山体抬升变形与水库枢纽区的水文地质结构模式有重大关系，本文采用文献[6]中数值计算模型。采用江垭水库[8，9]的简化地质模型，将整体模型分为大坝、灌浆帷幕、渗透系数相对较低的隔水层和渗透系数较大的含水层。整体三维计算模型范围取值如图1所示，以坝轴线分别取上游、下游800.00 m，左岸、右岸取450.00 m作为四周边界，底部高程-200.00 m作为底部边界。上游模拟计算水位高程236.00 m，下游模拟计算水位高程125.00 m。大坝为混凝土重力坝，大坝建基面高程114.00 m，坝顶高程245.00 m，坝基底宽102.00 m。坝基灌浆帷幕最大深度处在相对隔水层中，以起到隔水效果，相对隔水层厚度90.00 m。

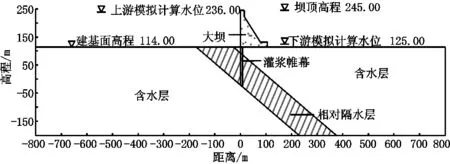
图1 模型地质结构图

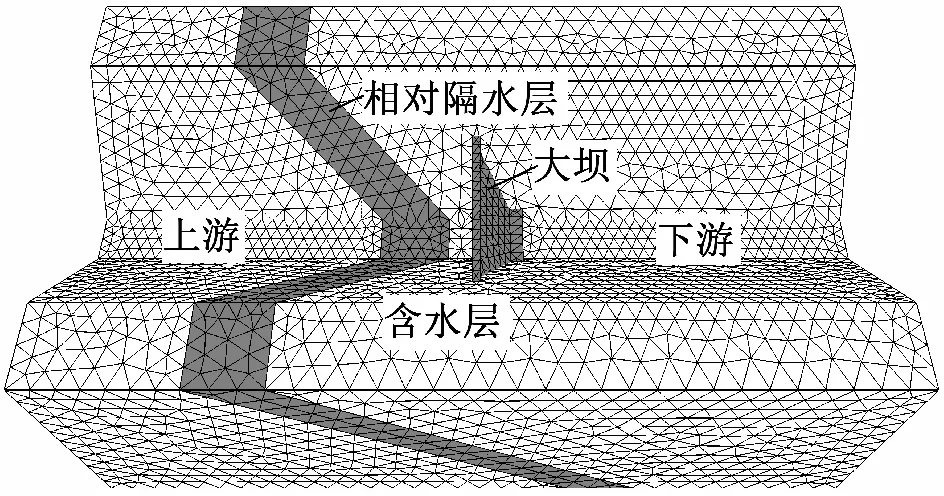
图2 计算模型网格图

图2为FLAC3D数值计算网格。采用四面体网格单元剖分，节点数共计16 719个，单元数共计88 097个。

2.2 初始条件

边界条件：四周竖向边界采用水平位移约束边界，模型底部采用位移固定边界；上游库水位以下表面按线性变化施加深度122 m库水压力，下游河道水位以下表面按线性变化施加深度11.00 m库水压力。水库库底表面及下游河道表面采用水头边界；模型底部及四周竖直边界采用不透水边界。

岩土体本构关系采用摩尔-库伦本构模型，渗流计算服从达西定律。基于文献[10]地质参数，本文数值研究采用的地质计算参数取值见表1。

表1 基本参数表

2.3 计算方案

2.3.1 变形模量计算方案

以表1参数作为基本参数，将含水层与隔水层变形模量分别按0.1、0.5、1.0、1.5、2.0、3.0倍的变换系数同比缩小或增大且其他参数保持不变建立计算方案，计算方案见表2。方案1坝基岩体含水层变形模量为1.10 GPa，相对隔水层变形模量为0.96 GPa。显然，相比实际重力坝坝址区基岩变形模量参数，方案1中所采用的参数明显偏小，实际勘测选址也不会将低参数岩层作为优选坝址区，但作为抬升变形规律定性分析过程，故也将其纳入计算方案中，为类似低变形模量坝址岩层的抬升变形分析提供参考。

2.3.2 渗透系数计算方案

将地质岩层分为渗透系数相差较大的相对隔水层和含水层。建立研究计算方案：第一种，采用表1基本参数，将相对隔水层的渗透系数确定不变，变换含水层岩体的渗透系数，其他力学及水力学参数均不变，考察含水层渗透系数变化对抬升变形的影响；第二种，将含水层的渗透系数确定不变，变换相对隔水层岩体的渗透系数，其他力学及水力学参数均不变，考察相对隔水层渗透系数变化对抬升变形的影响。计算方案见表3。

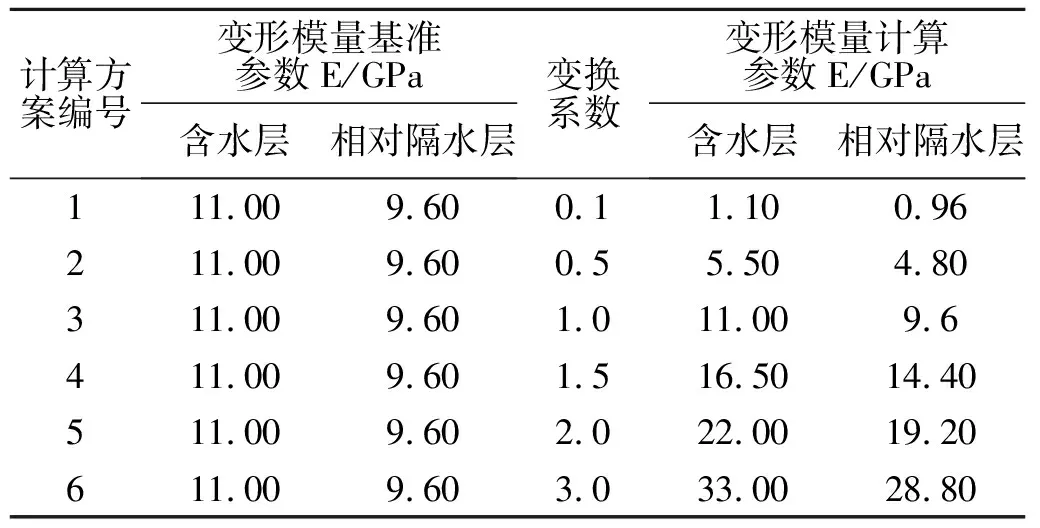
表2 不同变形模量计算方案表

2.4 计算步骤

按照以上拟定计算方案参数，分别赋予模型进行计算。计算步骤如下：首先，施加重力荷载生成初始自重应力场，接着，进行大坝一次性施工完成模拟，生成大坝施工完成后应力场，位移清除；然后，进行生成初始地下渗流场；最后，考虑流固耦合作用，施加上游蓄水荷载，模拟坝基及近坝山体抬升过程。

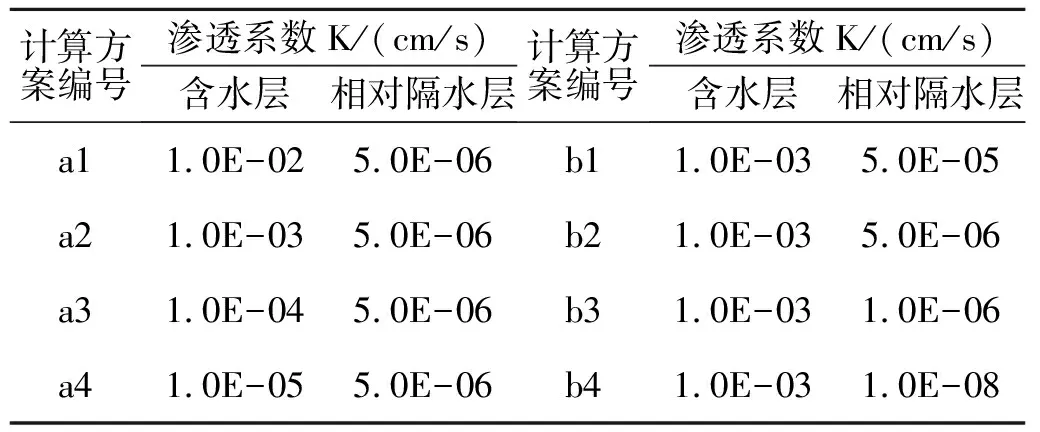
表3 不同渗透系数计算方案表

3 抬升变形空间位移分布规律

3.1 岩体变形模量对抬升变形的影响

表4为计算模型含水层与相对隔水层在不同变形模量参数下，最大抬升位移量及其最大抬升位置统计表。由表可知，随着含水层与相对隔水层变形模量不断增大，其抬升位移量呈现减小趋势。方案1中含水层变形模量为1.10 GPa，相对隔水层为0.96 GPa且倾向下游(倾角为38°)，计算最大抬升量为176.90 mm；当含水层变形模量增加到33.00 GPa，相对隔水层为28.80 GPa，其最大抬升量仅为1.5 mm，这表明坝基及近坝山体岩层变形模量参数对抬升变形的作用影响较大。而从最大抬升部位来看，最大抬升位移位置均出现在下游河道近坝山体，基本在坝轴线往下游200 m范围内。当变形模量足够大时，也出现在下游河道较远范围，可能原因是岩层变形能力有限，加上坝体重力荷载，渗透力不足以引起近坝河道岩层与近坝山体岩体上抬变形，因其最大抬升部位离坝体较远。

针对6种不同变形模量参数计算方案，图3给出了各方案抬升位移空间分布云图。由图可知，坝基及近坝山体岩层的变形模量参数不同时，其抬升变形量及抬升空间分布亦不同。由于水库上游库底水压力最大，造成最大沉降位移量出现在水库底部位置。在上游水库蓄水渗透力的作用下，坝体及下游近坝库岸、河道部分区域出现抬升变形，且抬升变形量随变形模量的增大而减小，而近坝山体的上抬变形很有可能由于边坡表面倾角的增大造成局部滑坡。而离坝体较远处的下游近坝山体、河床及高程较高山体依然产生沉降变形，由于不受水库蓄水导致的渗透力影响，故没有表现上抬趋势。由于计算模型中相对隔水层倾向下游(倾角38°)，因而无论是沉降变形还是抬升变形都是关于河道中心剖面对称分布。

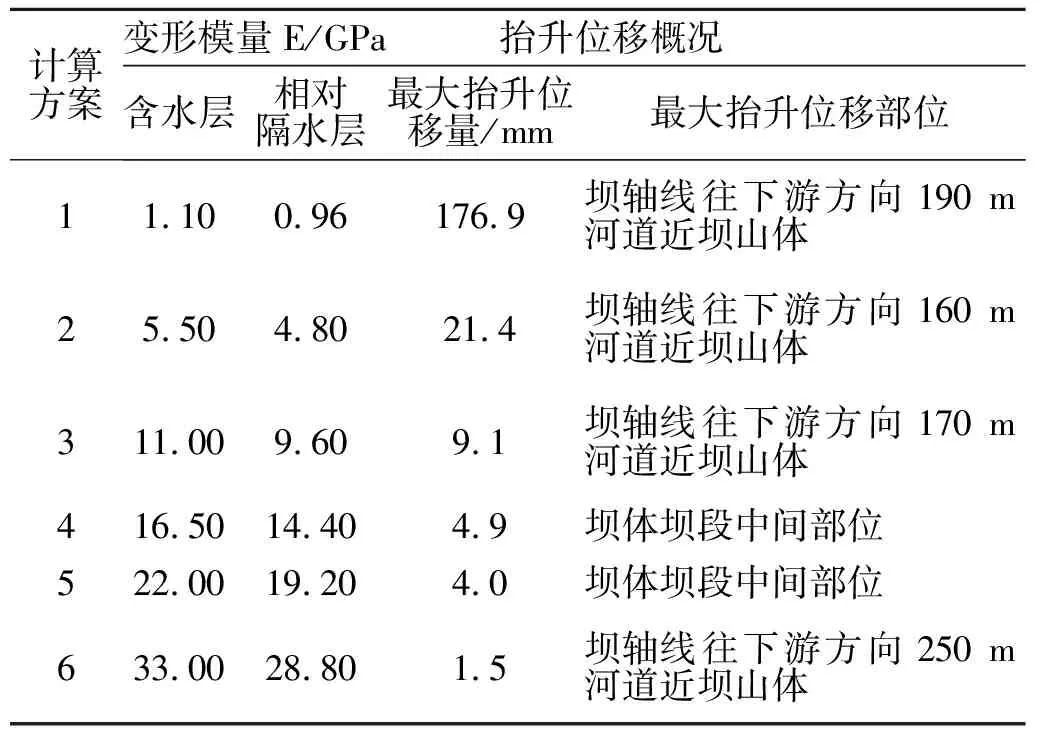
表4 最大抬升位移统计表

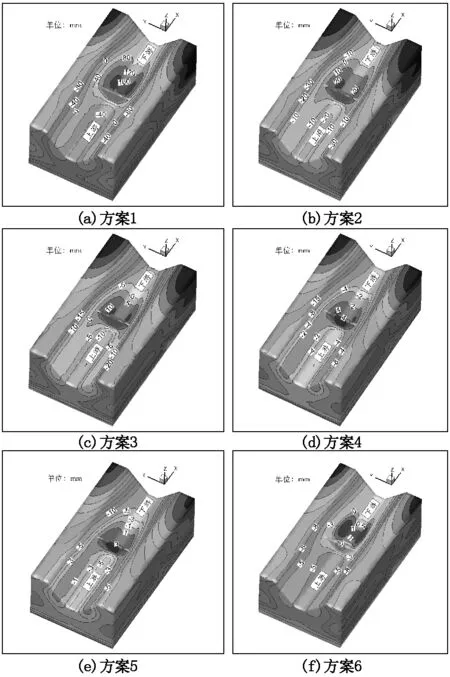
图3 变形模量敏感计算铅直位移空间分布图

图4给出了方案1至方案6计算模型在河道中心剖面的抬升位移等值线图。等值线云图直观的表达了河道中心剖面抬升位移分布情况。由图可知，随着变形模量的增大，河道中心剖面抬升位移减小；而上抬变形区域均发生在相对隔水层的上盘岩层，在抬升变形与沉降变形之间存有一位移变形为零的“分界面”。图中位移等值线表明，随着变形模量的增加，分界面逐渐减小，即抬升位移区域范围逐渐减小。

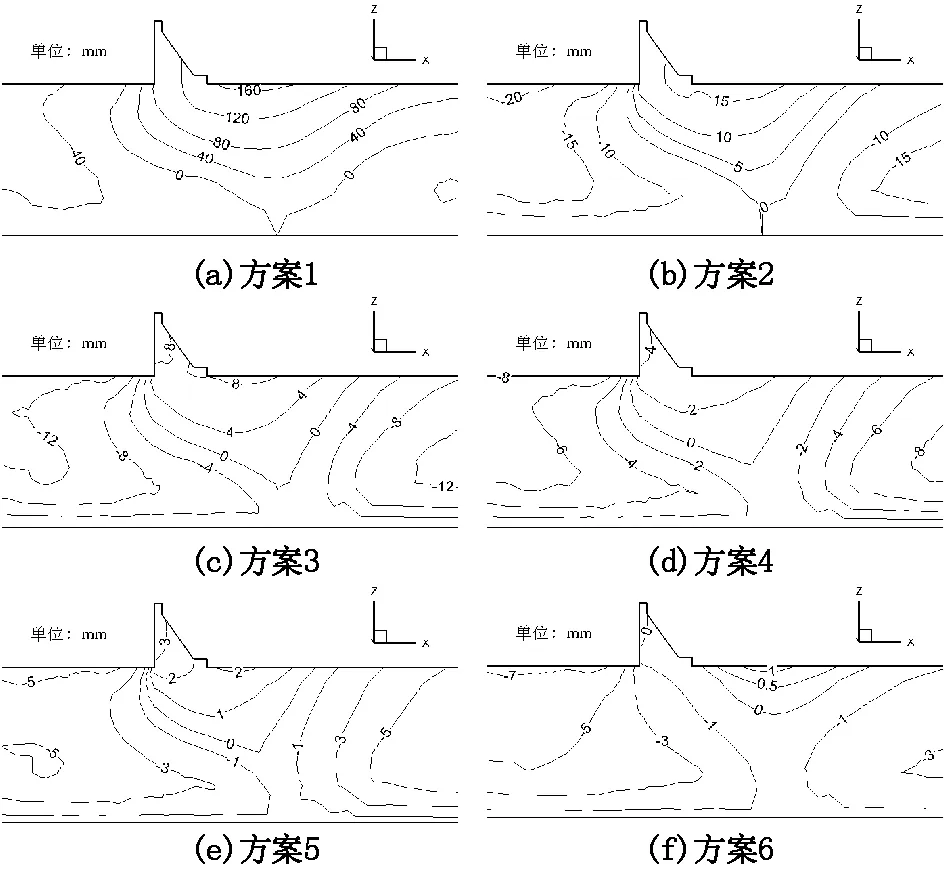
图4 河道中心剖面铅直位移分布图

3.2 岩体渗透系数对抬升变形的影响

3.2.1 含水层渗透系数变化对抬升变形的影响

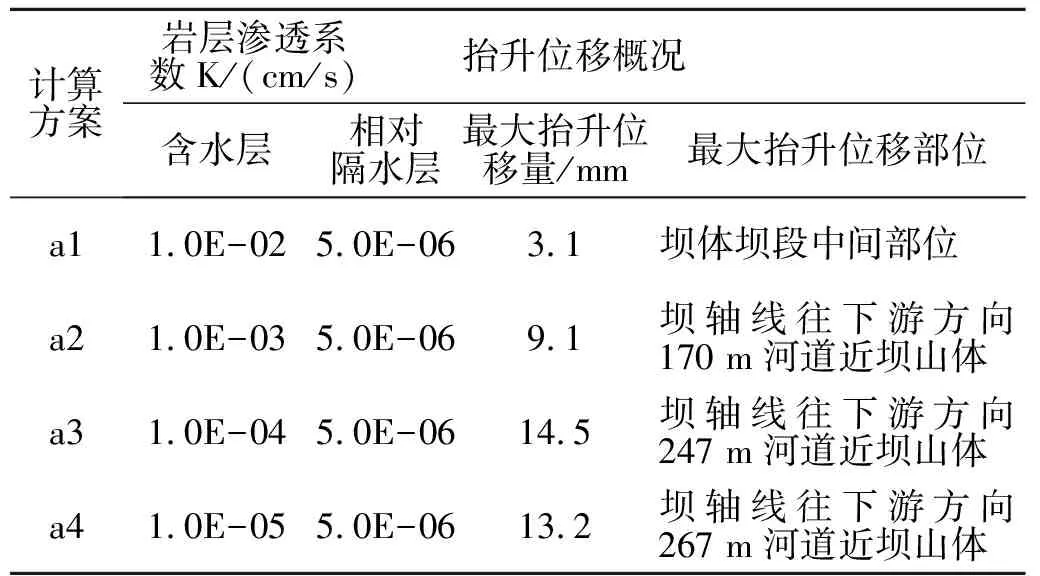
图5为计算模型相对隔水层渗透系数不变的情况下，含水层渗透系数变换计算的铅直位移空间分布图。由图可知，左右两岸铅直位移整体分布关于河道中心剖面对称，因库水压力荷载所致，各方案最大沉降位移均出现在水库库底。坝体及下游近坝河床、近坝山体出现不同程度抬升变形，最大抬升位移量均出现在下游近坝山体位置，其原因是：下游近坝河道由于承受最大河水压力，其抬升量比近坝山体抬升量略小；而近坝山体虽然承受一定水位的河水压力，但是在较大渗透力的作用下出现抬升，两种效应综合导致最大抬升量位置出现在近坝山体(见表5)。图中还表明，随着含水层渗透系数的减小，其抬升量整体呈先增大后减小趋势，抬升范围有向下游移动的趋势并且不断增大。因此，在含水层渗透系数不断变化的方案中，抬升变形的产生是含水层与隔水层渗透系数特定“组合”的结果，这种“组合”作用直接影响抬升变形的大小及范围。

图6为在河道中心剖面铅直等值线位移图。由图可知，与上述计算成果规律类似，在抬升变形与沉降变形之间存有一位移变形为零的“分界面”，并且随着渗透系数的减小，其河道下部岩体抬升范围越大，抬升量整体呈增大趋势。

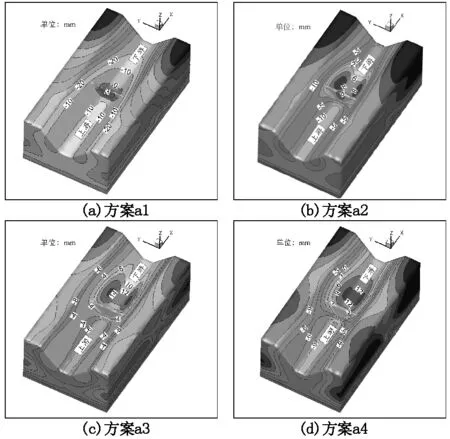
图5 含水层渗透系数变换计算铅直位移空间分布图

图6 河道中心剖面铅直位移分布图

计算方案岩层渗透系数K/(cm/s)抬升位移概况含水层相对隔水层最大抬升位移量/mm最大抬升位移部位a11.0E-025.0E-063.1坝体坝段中间部位a21.0E-035.0E-069.1坝轴线往下游方向170 m河道近坝山体a31.0E-045.0E-0614.5坝轴线往下游方向247 m河道近坝山体a41.0E-055.0E-0613.2坝轴线往下游方向267 m河道近坝山体

3.2.2 相对隔水层渗透系数变化对抬升变形的影响

图7给出了在含水层渗透系数不变的情况下，相对隔水层渗透系数逐渐减小的抬升位移空间分布图。由图可知，随着相对隔水层渗透系数的逐渐减小，抬升位移量并没有大幅度增加或减小，而是在9.0～10.0 mm范围内，抬升位移分布关于河道中心剖面对称，并且抬升范围基本一致(见图8河道中心剖面铅直位移等值线图)。可见，当含水层渗透系数处于某一定值时，相对隔水层的变化幅度不会太大，而是在某一范围值内变化。

表6为抬升位移统计表。由表可知，最大抬升位移量出现在下游近坝山体，并且与相对隔水层渗透系数变化不是单一相关关系，在下游近坝山体180 m附近变化。

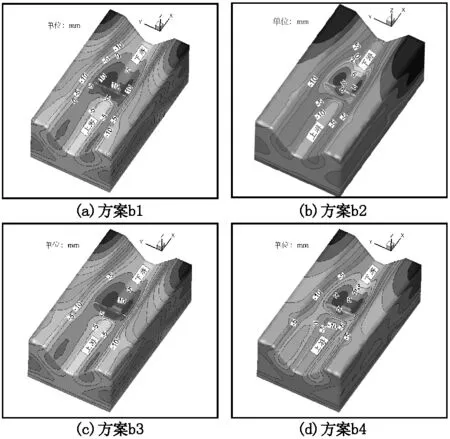
图7 相对隔水层渗透系数变换计算铅直位移空间分布图

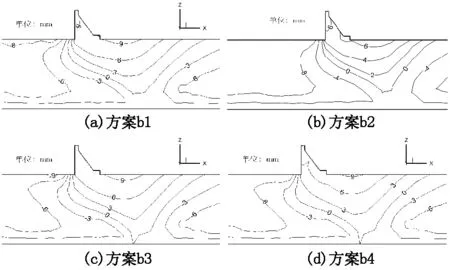
图8 河道中心剖面铅直位移分布图

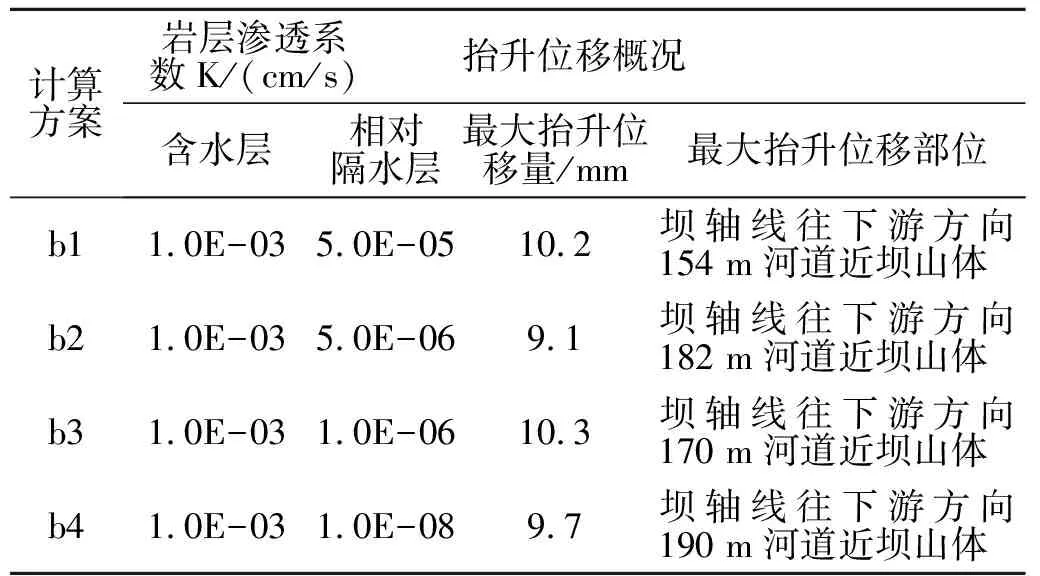
计算方案岩层渗透系数K/(cm/s)抬升位移概况含水层相对隔水层最大抬升位移量/mm最大抬升位移部位b11.0E-035.0E-0510.2坝轴线往下游方向154 m河道近坝山体b21.0E-035.0E-069.1坝轴线往下游方向182 m河道近坝山体b31.0E-031.0E-0610.3坝轴线往下游方向170 m河道近坝山体b41.0E-031.0E-089.7坝轴线往下游方向190 m河道近坝山体

4 结 论

本文基于应力场-渗流场耦合理论，采用三维数值模拟方法，针对岩体特性参数对抬升变形的影响展开研究，考察变形模量及渗透系数对抬升变形的敏感性影响规律，进一步揭示抬升变形的形成机制。得到以下结论：

(1)坝基岩体变形模量参数对抬升变形的影响较大，抬升变形量对变形模量大小较为敏感。随着岩体变形模量的增大，抬升变形量呈减小趋势；由于受水位差引起的渗透力及下游水位压力的综合作用，发生最大抬升部位均在下游近坝山体，而不是下游河床底部。上抬变形区域均发生在相对隔水层的上盘岩层，在抬升变形与沉降变形之间存有一位移变形为零的“分界面”，“分界面”的形成有可能导致岩土体及水工结构物产生剪拉变形。

(2)改变渗透系数对抬升变形规律及其空间分布的影响较不敏感。在相对隔水层渗透系数不变情况下，随着含水层渗透系数的减小，其抬升量整体呈增大趋势，抬升范围有向下游移动的趋势并且范围扩大；在含水层渗透系数不变情况下，随着相对隔水层渗透系数的减小，其抬升量并没有大幅增加或减小，而是稳定在一个范围值；空间位移分布形状相似；最大抬升位移部位同样发生在下游近坝山体。近坝山体抬升变形过大有可能造成边坡局部滑坡。