考虑基质和酸压缝应力敏感性的 产能预测模型

郑子君，余 成

(1.重庆理工大学，重庆 400054；2.重庆交通大学，重庆 400074)

0 引 言

非常规油气田开发中普遍遇到应力敏感性现象：随着地层有效应力升高，储层渗透率明显降低[1]。对储层基质渗透率的应力敏感性的定量评价主要是在变围压渗流实验的基础上，采用不同的拟合模型描述渗透率与净应力的关系[2-5]。文献表明，储层基质的应力敏感性对油气井的稳态产能有显著的影响[6-11]。经过储层改造的油气井的产能也同样受到基质应力敏感性的影响[12-17]。调研发现，在进行应力敏感储层酸化压裂井的产能预测分析时，现有文献通常只考虑了基质渗透率的变化[5，12-17]，而忽略了酸压缝导流能力也会随地层压力变化而改变的现象，这不符合实验和数值模拟的结果[18-20]，可能导致预测结果在地层压力衰竭后出现较大偏差。因此，提出在现有应力敏感储层产能预测模型基础上，考虑酸压缝导流能力变化的影响。通过离散元数值模拟，确定影响导流能力变化的因素，在此基础上选取合适的经验公式，将酸压缝导流能力的变化抽象为等效表皮系数的改变，从而对产能预测模型进行修正。采用库车西部某井的生产数据对修正后的模型进行了验证。

1 应力敏感储层的产能预测模型

应力敏感储层基质的渗透率随地层压力变化的规律，可在实验基础上采用各种数学模型描述。一种常见的模型是，总围压不变时，地层压力和渗透率的关系满足指数规律[5，13-16]；在指数模型的基础上，进一步考虑渗透率可部分恢复，则渗透率应力敏感模型为：

K=K0exp(-βαΔpmax)·exp[βreα(Δpmax-Δp)]

(1)

式中：K和K0分别为当前地层压力和初始地层压力下的渗透率，10-3μm2；β、βre分别为应力敏感性指数和渗透率恢复指数，MPa-1；α为比奥常数；Δp、Δpmax分别为当前地层压力的降幅和岩石经历的历史最大压力降幅，MPa。模型参数βre、β均由实验测出，且通常βre<β，即地层压力恢复后渗透率不能完全恢复[12]。

假设井下渗流是平面径向稳态的，将式(1)代入径向流动的达西定律求解，得油井地面产量Qo与生产压差Δp′的关系：

(2)

式中：Qo为油井地面日产量，m3/d；B为无因次体积系数；re为供给半径，m；rw为井眼半径，m；Δp′为生产压差，MPa；μ为原油黏度，Pa·s；h为储层厚度，m；S为储层改造影响后的等效表皮系数。

对于可压缩气体，在低速渗流情形下可引入平均压差和平均流量的概念，按式(2)计算；或假定气体为等温理想气体[21]，此时，将式(1)和波义耳方程代入达西定律，可推得气井地面稳态产量为：

(3)

在常规产能预测中，等效表皮系数S通常被当作常数处理，即用初始表皮系数S0代替。然而，考虑到酸压缝的导流能力会随着地层压力变化而变化[18-20]，S应为地层压力的函数。

为提高气田应力敏感储层产能预测的可信度，可根据地层压力的变化对式(2)、(3)中的S进行修正。

2 酸压缝导流能力变化幅度的影响因素

对于不同情形的酸化压裂缝，地层压力变化时，导流能力的变化程度不同，因此，表皮系数的修正幅度也不同。为确定导流能力变化幅度与裂缝参数的关系，采用离散元方法对酸压井的生产过程进行流固耦合模拟。

建立以单井为中心的储层准三维模型，边界受原场地应力作用，过中心沿最大主应力方向有1条矩形酸压主缝(图1)。模型中，液体可以同时在裂缝和基质中流动；裂缝开度可随裂缝贴合面净应力的变化而改变；基质可以发生弹性变形，但暂不考虑基质应力敏感性。分别以20、40、60 MPa的生产压差模拟开采，直至达到稳定流动状态。

图1 带有酸压主缝的储层离散元模型

稳态生产时，储层的归一化压降分布和相对采油指数见图2、3。随着生产压差增加，压降漏斗的形状改变，相对采油指数减小，表明酸化压裂缝的导流能力随着地层压力的变化而变化，即酸压缝也存在“应力敏感性”。

利用控制变量法，变更单个裂缝参数，计算压降分布以及采油指数，并进行对比(图2、3)。可以看出，裂缝刚度(改变单位裂缝开度所需要的应力增量)越小，初始开度越小，裂缝长度越长，压降漏斗形状和采油指数随生产压差的变化越明显，即酸压裂缝的“应力敏感性”越强。

实际工程中，酸压裂缝形状复杂，裂缝刚度和初始长度难以直接测定，但根据酸化压裂的机理，酸压缝刚度与岩体强度正相关[19，22]。另一方面，根据定义，裂缝初始开度越大，长度越短，其初始无量纲导流系数CFD0就越大。由此可得，酸压缝等效表皮系数的修正幅度与岩体强度、初始无量纲导流系数均呈负相关，而岩体强度、初始无量纲导流系数可以通过实验和工程手段获得。

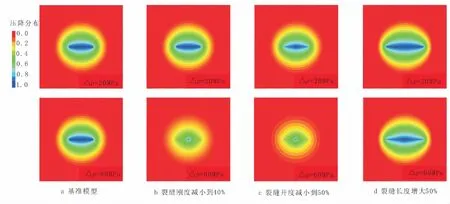
图2 稳态流动时压降漏斗分布(已对生产压差归一化处理)

3 酸压井等效表皮系数的修正

地层压力降低时，有效地应力升高，裂缝的无量纲导流系数降低，等效表皮系数则随之升高。根据现有文献提出的地应力、无量纲导流系数、表皮系数之间的经验规律，可对表皮系数进行修正。在对此类经验关系考察后发现，结合Nierode-Kruk公式[23]和Prats酸压评估图板[24]，得到的表皮系数修正公式符合前述数值模拟的定性结论，且计算结果和实例吻合较好。Nierode-Kruk公式指出，酸压缝导流能力与闭合应力间存在指数关系：

Kfw=C1exp(-C2σc′)

(4)

式中：Kf为裂缝等效渗透率，10-3μm2；w为开度，m；σc′为裂缝贴合面的平均有效闭合应力，MPa；C1与C2均为模型参数，10-3μm2·m·MPa-1，其经验取值方法由Nierode和Kruk给出[23]。

式(4)两边同时除以裂缝半长xf和基质渗透率K0后取对数，取增量形式，得：

(5)

式中：Δ代表取增量。

ΔlnCFD=-C2αfΔp′

(6)

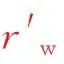
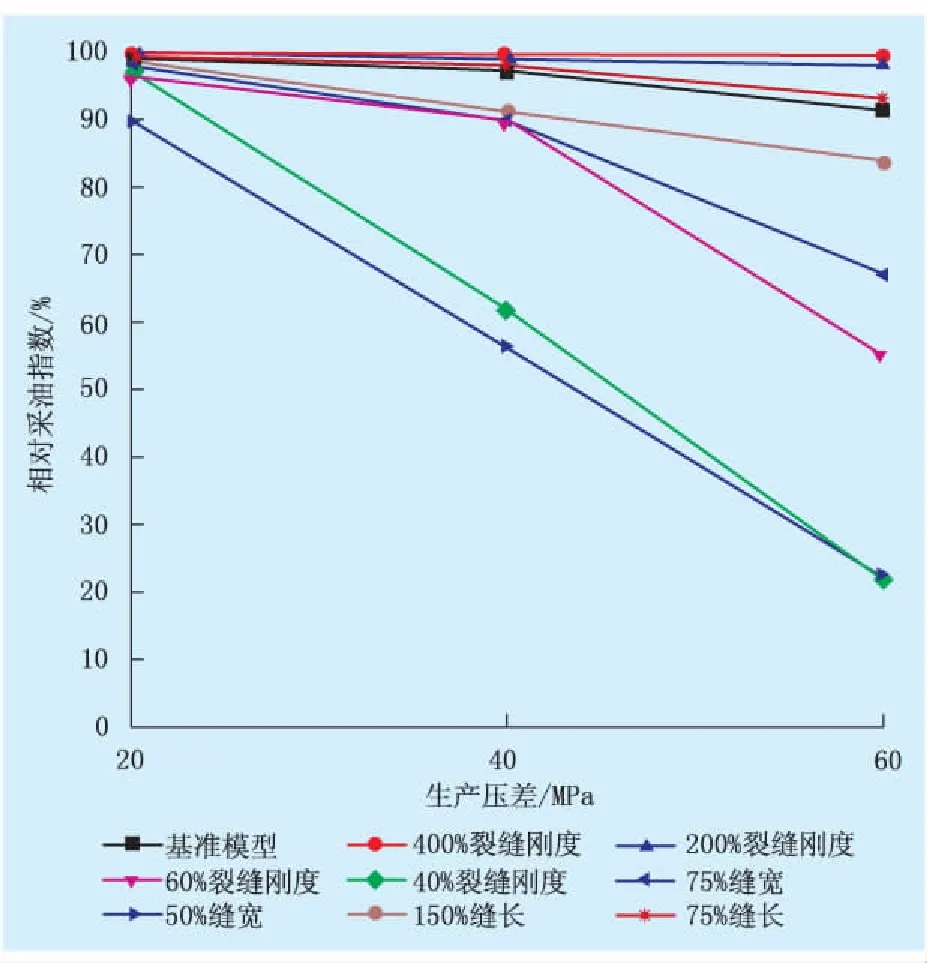
图3 相对采油指数随生产压差的变化规律(对生产压差无穷小时的指数归一化处理)

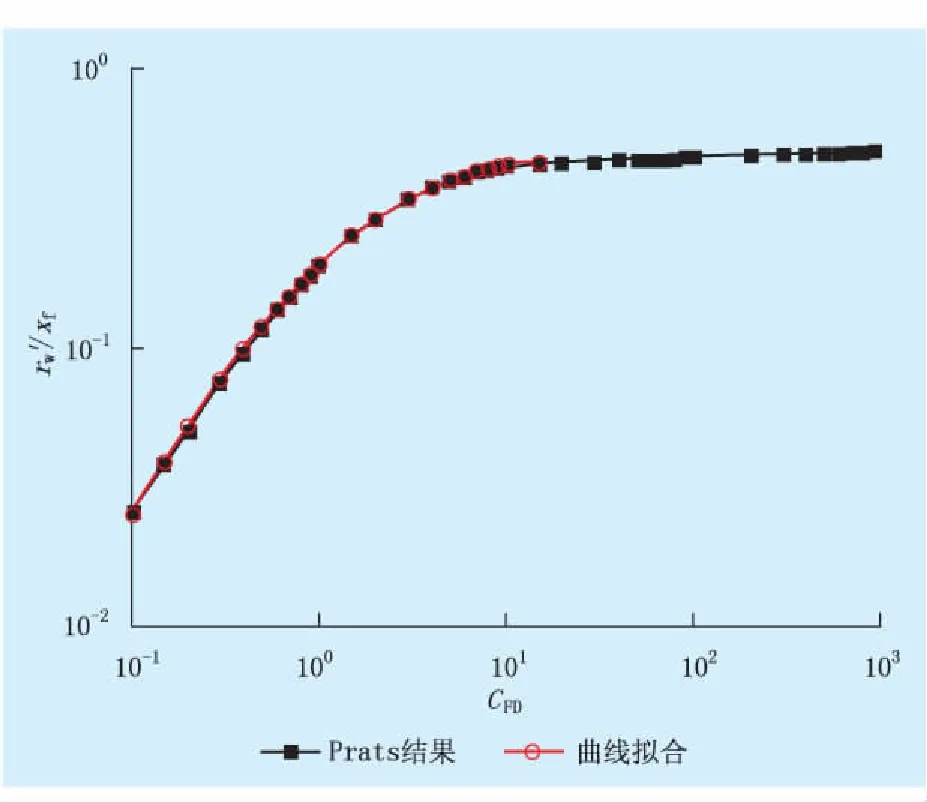
图4 无量纲导流系数和无量纲等效井半径的关系

由图4可知，无量纲等效井径在CFD>20时趋于常数；在CFD≤20时(适合库车地区大部分情形)，可用下式拟合：

(7)

式中：rw′为等效井径，m。

根据表皮系数S的定义，其修正量可表示为：

(8)

注意到裂缝半长xf和井径rw通常不随地层压力变化改变，上式右端第2项为0。对式(7)取增量形式，并与式(6)一起代入式(8)，得：

ΔS=(0.65-0.23lnCFD0)αfC2Δp+0.115(αfC2Δp)2

(9)

式(9)即为地层压力变化时表皮系数的修正公式。根据Nierode-Kruk公式，C2与岩石强度σs呈负相关，因此，式中修正量ΔS与岩石强度σs、初始无量纲导流系数CFD0均呈负相关关系，和前述模拟定性结论一致，符合物理规律。

另一方面，若逐渐降低生产压差，使地层压力恢复，则裂缝导流能力可能部分恢复。为考虑裂缝导流能力恢复对产能的影响，引入恢复系数θ∈(0，1)，并将表皮系数修正量表示为：

ΔSre=(1-θ)ΔSmax+θΔS

(10)

式中：ΔSmax为历史最大生产压差Δpmax下按式(9)算得的修正量；ΔS为当前生产压差Δp下算得的修正量。

显然，θ越大，裂缝导流能力变化的可逆性越强。θ=0，1时分别对应着导流能力变化完全不可逆情形和完全可逆情形。利用式(9)、(10)可以修正复杂地层压力变化路径下的表皮系数，从而对式(2)、(3)中的预测产能进行修正。

4 案例分析

库车西部某致密储层凝析气井，酸压后的生产情况见图5[12]。该井于2015年5月恢复生产，产量逐渐下降，至10月达到稳定，假定此后该井处于稳态流动状态，继续缓慢增大生产压差，日产量呈减速上升趋势，直至生产压差约为28 MPa时，产量达到峰值；之后进一步升高压差，产量反而降低，其间未见明显地层出砂；至2016年5月，生产压差达到峰值45 MPa，短暂关井后降低至20 MPa左右生产，发现产量不能恢复到前期相同压差下的水平。

图5 库车西部某井的生产情况

根据分析，初步怀疑该井产量受到储层应力敏感性的影响。由于该井地层压力与露点压力差较大，分析时可按单相气体流动进行计算。若按照文献中应力敏感性储层的产能预测公式，无论采用何种参数，产量总与压差正相关[5，9-10]，与实际现象不符。因此，采用提出的模型对生产压差与产量的关系进行定量分析。该井部分参数见表1。

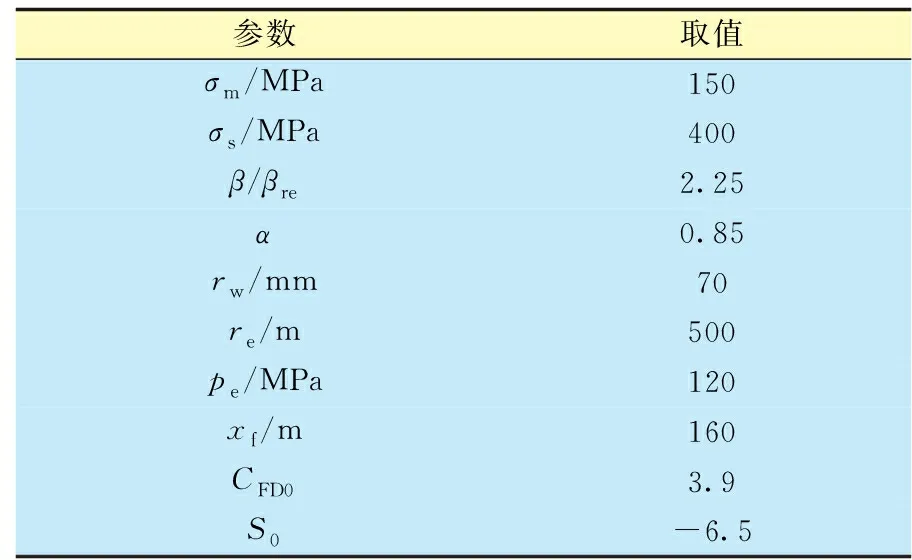
表1 库车西部某井部分参数

根据离散元模拟结果，主缝内平均压降约为生产压差的85%，即压降折减系数αf=0.85。酸压缝导流能力恢复系数θ取0.7，则修正后的稳态产量与生产压差关系如图6中蓝色线所示，可见预测结果与实际数据吻合良好。

模型预测结果表明，初期随着生产压差的增加，稳态产量先单调增加，当压差达到27 MPa时(实测约28 MPa)，产量达到峰值，之后随生产压差增加，产量反而下降。若生产压差持续升高至45 MPa后再逐渐降低，由于基质和酸压缝的导流能力均发生不可逆的损害，产量将低于前期同压差产量。上述现象与实际完全吻合。由于裂缝闭合后重新张开需要更多能量，生产压差下降阶段的实测数据随机分散性较大，模型预测仅与部分数据点相近。

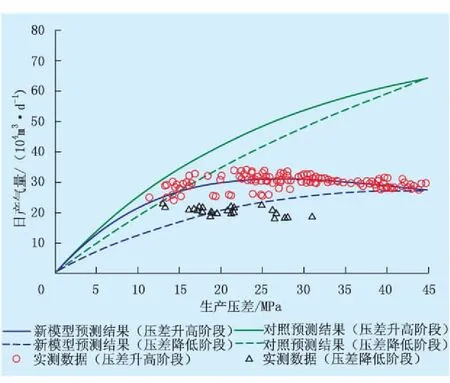
图6 库车西部某井生产压差和稳态产量关系

作为对比，图6给出相同模型参数下，不修正表皮系数、只考虑基质应力敏感性的产量预测结果。可以看到，高生产压差下的产量被明显高估，这可能对井区开发策略的制订产生误导。

5 结 论

(1) 通过进行流固耦合的离散元模拟，验证了酸压裂缝导流能力随生产压差变化的现象。参数分析表明，岩石的强度和裂缝初始形态是影响酸压缝导流能力变化幅度的因素。

(2) 提出对不同压差下酸压缝等效表皮系数进行修正，得到能同时考虑基质应力敏感性和酸压主缝导流能力变化的产能预测模型。模型还考虑了地层压力恢复时基质和裂缝导流能力的恢复，可用于地层压力变化路径较复杂时的情形。

(3) 新模型指出，在生产压差单调增加时，产量先期上升，且上升趋势逐渐减缓，有可能在达到极值后转而下降，出现压差和产量呈负相关的现象；生产压差升高后再减小到初始压差时，产量低于初始产量；预测结果和实例吻合。

致谢：中国石油塔里木油田公司地质工程一体化团队的领导和专家在地质认识、实验处理、资料收集等方面为本文提供了重要帮助，在此表示诚挚的谢意！