基于EEMD-BBO-ELM的短期风电功率预测方法

时 彤，杨 朔

(大唐东北电力试验研究院有限公司，吉林 长春 130012)

0 引言

进入21世纪以来，人类面临的环境危机越来越严重，对传统能源的利用形式进行改革的呼声日益高涨。在此背景下，清洁能源登上了历史发展的舞台，且在近年的发展中取得了良好的环境效益和成本效益，其中最具代表的清洁能源非风电莫属；但众所周知，由于风能本身存在的有悖于电力系统稳定性要求的间歇性、随机性和不确定性等诸多缺陷，大规模的风电并网一直是一大难题。目前，业内普遍较为认可的解决这一难题的技术手段便是提高风电功率的预测精度[1-3]。风电功率序列通常具有较高的复杂度，混沌特性明显，规律性不强，要准确把握其本质往往具有较大难度，基于此本文提出首先利用集合经验模态分解算法(ensemble empirical mode decomposition，EEMD)对风电功率序列进行分解，以准确把握其内在的规律，之后再利用优化后的极限学习机算法进行风电功的短期预测。该算法可以有效地提高短期功率的预测精度，从而可以为优化电网调度，降低运行成本，维持电网稳定运行提供重要支撑。

1 经验模态分解方法原理及其改进

1.1 经验模态分级

经验模态分解(empirical mode decomposition,EMD)是一种自适应时间序列分解技术，采用Hilbert Huang变换筛选非线性信号直到信号达到稳定状态[4]。EMD算法认为某一时间序列是由不同类型下的振荡模式共同构成的，每种振荡模式下的本质特征都隐藏在合成的序列中。因此，每个振荡模式下的本质被EMD分解后便可从原始序列中剥离出来[5-6]。EMD是基于信号的自身尺度来进行分解，理论上可以应用于任何类型的时间序列，但是其对波动性较大的波形进行处理更具有先天性优势。进行EMD分解后，本征模态分量(intrinsic mode function，IMF)需符合以下2个条件：

(1) 序列中的局部极值点的个数和信号过零点的个数相差不超过1个。

(2) 在序列定义域范围内的均值趋于0。

EMD分解过程如下：

(1) 求解原始序列X(t)中的所有极值点，后拟合出原始序列的上包络线l1(t)和下包络线l2(t)。

(2) 求解2条包络线的中位值。

m1(t)=[l1(t)+l2(t)]/2

(1)

(3) 令h1(t)=X(t)-m1(t)，此时若h1(t)不满足IMF分量的条件，则重复上述步骤，直至k次迭代后h1k(t)满足条件，此时便有C1(t)=h1k(t)。

(4) 将IMF1分量抽离出原始序列，后将抽离IMF1分量后的序列r1(t)=X(t)-C1(t)再视为原始序列重复进行分解。如此便可获得n个IMF分量，直至剩余分量rn(t)满足单调性时停止继续分解。此时最终分解得到的序列为

(2)

式中：Ci(t)为原始序列的IMF分量；rn(t)为原始序列的剩余分量。

1.2 集合经验模态分解

EEMD是指在模态分解时的序列加入白噪声序列，该白噪声的分布服从正态分布，此举可有效抑制传统模态分解中存在的模态混淆问题[7]。由于在风电功率数据的实测过程中，由于各个环节间的传输和协调不通畅，往往会造成异常脉冲干扰等现象，这些异常脉冲会对模态分解产生误导，使得分解出的IMF分量不够准确，因此便会出现模态混叠现象，从而使得分解效果大打折扣。而集合经验模态分解对分解过程进行了改进，从而可有效避免模态混叠现象[7-8]。集合经验模态分解对传统模态分解的改进过程如下：

(1) 在原始风电功率序列中增加白噪声序列(该序列服从正态分布)，形成新风电功率序列。

(2) 对由步骤(1)构成的新序列进行EMD分解。

(3) 将上述2步迭代m次，需要注意的是在每次开始迭代时都需在序列中增加新的不同幅值的白噪声序列，后对得到的m组IMF分量求均值，便可得到原始序列的IMF分量。

2 生物地理学算法及其改进

2.1 生物地理学

生物地理学算法(biogeography-based optimization，BBO)考虑了大空间、长时间尺度范围内的不同栖息地的进化，由该栖息地中生物的迁入、迁出和变异来挖掘出栖息地不同生物种群间的相互联系。在各物种的相互平衡下，生态系统演化的最终结果将是一种相对稳定、平衡的状态。因此，BBO算法是一种受到生物地理学系统间变异效应和种群迁移启发而形成的一种优化算法。

在BBO算法中信息的交互机制所对应的是栖息地中生物种群的迁入和迁出。也就是说在BBO优化算法中是通过迁入和迁出操作来完成信息共享的，若从j迁移到i，则有

Hi(SIV)←Hj(SIV)

(3)

式中：Hi(SIV)和Hj(SIV)分别为第i步和第j步的迁移操作；SIV为适宜度指数变量。

若在第k个栖息地总共有Ck个物种的概率为Pk，Ck=1,…,smax，其中smax表示种群数目的最大值，则从t时刻到t+Δt时刻，Pk将变为

(4)

式中：λk为在第k个栖息地物种数目为Ck时的迁入率；μk为在第k个栖息地物种数目为Ck时的迁出率。迁入率λk和迁出率μk与k的关系如下：

(5)

式中：I为迁入率函数的最大值；E为迁出率函数的最大值。

为提高BBO算法的寻优能力、增加其鲁棒性，可在以上基础上引进不同的迁移模型：

(6)

为模拟真实栖息环境中发生的各种突变、栖息地生物种群的多样性，同时为进一步提升BBO算法的寻优性能，需要对其中的每个候选解的每个特征都依据变异率进行变异操作。设栖息环境突变概率为mk，栖息地的物种数量为Ck时所对应的概率为Pk，则有

(7)

式中：Pmax为Pk的最大值；M为突变率的最大值。

值得注意的是，研究中应规避处于平衡点的栖息地发生突变，因为处于平衡点的候选解有最大的得到改善的概率，因此平衡点发生突变可能反而会对寻优过程产生破坏。

2.2 极限学习机算法

极限学习机(extreme learning machine, ELM)是一种新型的前馈神经网络算法，其是在单隐层前馈神经网络(single-hidden layer feedforward neural networks，SLFNs)的基础上形成的一种新型学习算法[9-11]。

假设训练集为(xj,tj)∈Rn×Rq，j=1,…,N，xj=[xj1,xj2,…,xjn]T，tj=[tj1,tj2,…,tjq]T，则此时对含有L个隐含层节点，含有q个输出节点的SLFNs网络而言，ELM网络的输出便可表示为

(8)

式中θi为第i个隐含节点与输出节点间的权值向量；h()为特征映射；xj为神经网络的输入；wi,bi均为特征映射参数[12-14]。

(9)

若以矩阵形式表示，有

HB=T

(10)

式中：H为隐含节点输出矩阵；B为输出的权值矩阵。

为进一步增强网络的可推广性和其数值解的稳定性，可考虑利用回归法和Tikhonov正则化，给出正则化系数η后，式(8)的最小二乘解便可记为[15-17]

(11)

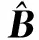
2.3 BBO-ELM算法

单输出结构的ELM网络中，权值向量θ由隐含节点的参数wi和bi求得，由于参数是随机获得的，因此其准确性无法保证。为获得更好的性能，ELM算法更愿选取较多的隐含层节点，但是对不同类型的训练集而言，网络隐含节点的多少并不直接决定网络的学校能力，较多的隐含节点有时反而会降低网络的学习能力。基于此，本文引入BBO算法对ELM网络的结构和其参数选取进行合理的优化，以期提高ELM算法的性能。对ELM网络的优化过程主要包括对输入变量选取的优化、隐含层节点数目的优化和激活函数优化3个方面[18]。

BBO-ELM方法的具体实现步骤如下：

(1) 初始化参数。给出最大迁入率I、最大迁出率E、全局迁移率pmod、全局最大突变率M、最大进化代数gmax、精英个体保留数z。

(2) 根据均匀分布的随机数来确定初始的种群R=[p1,p2,…,pm]。

(3) 计算种群中所有pk的栖息地适宜度指数(habitat suitability index，HIS)，并将求取的HIS降序排列，计算栖息地pk的物种数量、迁入率λk和迁出率μk，保留按HIS降序排列的前z个“精英”。

(4) 利用全局迁出率pmod判断对“精英”之外的个体是否需要进行迁移。

(5) 按照式(3)对栖息地的Pk进行更新，同时对按降序排列HIS的后1/2个体产生一个随机数r。此时若变异率大于该随机数，则说明需要对该个体进行变异操作，之后再重新计算HIS。

(6) 排除栖息地中存在的重复种群，假设栖息地中存在pk=pv,k≠v，则需通过初始化来随机产生一个新栖息地来替代重复的种群，同时更新HIS。

(7)g=g+1,若满足g=gmax，则进化结束，若不满足则转到步骤(3)。

3 建模过程及其预测结果评价指标

3.1 建模过程

首先利用集合经验模态分解对原始风电功率序列进行分解，后针对不同的IMF分量分别采用BBO-ELM算法进行预测，之后再把全部分量的预测值进行累加便能够获得实际的预测结果。利用本文算法进行预测具体流程如图1所示。

图1 EEMD-BBO-ELM预测流程图Fig.1 EEMD-BBO-ELM prediction flow chart

3.2 预测结果评价指标

为了能够准确衡量预测模型的预测性能，采用归一化后的绝对平均误差eNMAE及归一化后的均方根误差eNRMSE两个指标作为评价指标。

4 算例分析

本文实验数据为吉林省某风电场的实测数据，该风电场装机容量为99 MW，实测数据的采样间隔为15 min，选取其中2 000个点的风电功率数据进行仿真实验。其中前1 800个点的数据作为训练样本，后200个点的数据作为测试样本。

图2为选取的风电场2 000个样本数据的时间序列曲线，将该曲线经过EEMD分解过程后，则得到如图3所示的分量曲线。

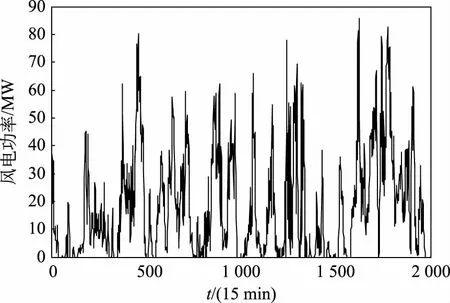
图2 风电功率原始时序曲线Fig.2 Original time series curve of wind power

图3 EEMD分解结果Fig.3 EEMD decomposition results

预测模型可由BBO或其他优化算法优化的ELM方法构建。实验中，ELM的隐层节点数目初始化为500，BBO算法的pmod=1，I和E均为1，突变率mk=0.005，精英数量z为2。粒子群(particle swarm optimization，PSO)算法的加速度因子为0.3，惯性权重为0.3。遗传算法(genetic algorithm，GA)中的交叉概率pc=1，变异率pm=0.1。尺度因子α选择为[0.5,2]范围的随机数。初始温度T0=100，退火因子β=0.95，迭代次数g=250。

4.2 预测结果分析

由图3可知经EEMD分解后的IMF分量与图2所示的原始风电功率序列相比，其波动变化较为平稳，频谱特征也由IMF分量从高频到低频依次表征出来。

为验证本文所提EEMD分解和BBO-ELM模型的预测性能，建立基于ELM、EEMD-ELM、BBO-ELM、EMD-BBO-ELM和EEMD-BBO-ELM这5种模型来验证本文所提模型的优越性。

表1统计了不同预测模型的预测误差，可看出EEMD-BBO-ELM的精度较单一的ELM预测模型有很大提高，且由BBO-ELM预测模型的预测结果明显好于ELM和EEMD-ELM。可见BBO算法对于优化ELM的网络参数具有至关重要的作用，而对原始风电功率序列既进行分解又进行网络参数优化的EEMD-BBO-ELM预测模型在5种预测模型中预测结果的精度最高。图4为某日的5种预测模型的预测曲线与实际曲线对比情况。由图4可知，经过EEMD分解后采用BBO-ELM模型进行预测时预测曲线和实际曲线的吻合度为5种预测模型中最高的，由此便可说明采用EEMD分解方式和BBO参数优化方法更大程度地提高了ELM的预测性能，从而有效提高了短期风电功率的预测精度。

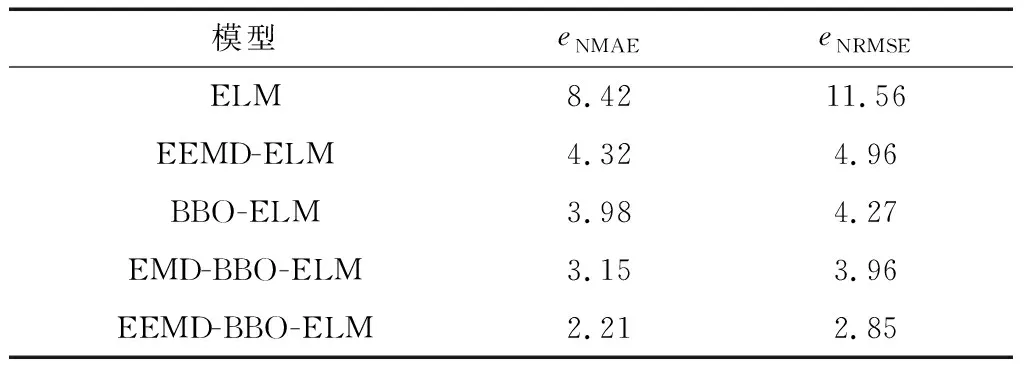
表1 不同预测模型的预测误差(风电场1)Table 1 Prediction error of different prediction models (wind farm 1)

为进一步验证本文所提模型的普适性和优越性，对吉林省另一个风电场数据进行实验分析。该风电场总装机容量49.5 MW，较之前实验的风电场规模小，同样采用上述5种预测模型对比分析。表2为不同预测模型的预测误差，本文所提模型的风电功率最优预测曲线如图5所示。

由表2可知，EEMD-BBO-ELM预测模型的eNAME和eNRMSE较ELM分别降低了61.05%和50.79%，较EEMD-ELM的eNAME和eNRMSE降低了47.46%和41.96%，较BBO-ELM的eNAME和eNRMSE降低了39.49%和37.69%，较EMD-BBO-ELM的eNAME和eNRMSE降低了31.30%和24.39%，说明经过BBO算法进行参数优化后的ELM预测模型具有更明显的优势。再在此基础上，经EEMD分解后，采用BBO-ELM模型可有效提高预测能力。结合图5可知，EEMD-BBO-ELM模型与其他组合模型相比其预测效果最佳，能够获得较高精度的短期风电功率预测结果。该结论与对上文装机容量为99 MW的风电场的预测结果得出的结论一致。

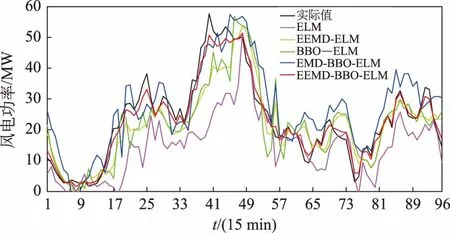
图4 实际曲线与5种预测模型的预测曲线(风电场1)Fig.4 Prediction curve of actual curve and five prediction models (wind farm 1)

模型eNMAEeNRMSEELM6.657.56EEMD-ELM4.936.41BBO-ELM4.285.97EMD-BBO-ELM3.774.92EEMD-BBO-ELM2.593.72

图5 实际曲线与5种预测模型的预测曲线(风电场2)Fig.5 Prediction curve of actual curve and five prediction models (wind farm 2)

此外，EEMD-BBO-ELM模型具有很高的预测效率，在预测过程中所用时间方面，采用EEMD-BBO-ELM进行实验分析时预测200个点的预测时长为40.56 s，较只采用ELM进行预测时多10.02 s，可满足预测的基本需求。

5 结论

EEMD-BBO-ELM模型要优于BBO-ELM模型，说明了进行EEMD分解的有效性，有效降低了IMF不规则性对预测结果的影响，提高了预测性能；BBO-ELM模型优于ELM模型，说明了采用BBO算法对ELM模型参数进行优化的有效性，且BBO-ELM模型优于EEMD-ELM模型，说明在采用ELM模型进行预测时，进行参数优化更加重要。

采用不同风电场的数据对EEMD-BBO-ELM模型进行验证，证明了本文所提分解模型的稳定性和普适性；BBO算法进一步提高了ELM的预测能力，EEMD-BBO-ELM可有效地跟踪风电功率的变化规律，提高预测精度。