阈值阵列系统中TCM编译码的随机共振现象
李 恒,王友国,翟其清
(南京邮电大学 通信与信息工程学院,南京 210003)
0 引言
随机共振(Stochastic Resonance,SR)[1-2]最初是由意大利物理学家Benzi等人在解释地球远古气象中冰期与暖期周期性交替出现而提出的;此后被用来描述一种现象——非线性系统当中,因噪声的存在改善信号的处理和信息传输。众所周知,在线性系统当中,噪声总是对信号的传输与测量起到消极作用;但是,经过研究发现,在非线性系统当中,适量的噪声可以提高系统的性能,改善系统的输出[3]。此后,随机共振被广泛应用,如在故障诊断、图像增强、微弱信号检测等方面的应用。
在信号与信息处理领域,国内学者采用神经元模型和耦合神经元网络将SR现象用于改善周期性语音信号的性能[4]和增强脉冲信号传输[5]。此外,还采用阈值非线性系统,利用不同的测度(如互信息[6-7],信噪比[8-9]等)研究SR现象的存在及应用,并取得很多成果。在实际的通信中,调制和信道编码等技术被广泛使用,在调制和编码的过程中总是伴随着噪声的存在,文献[10][11]研究了二进制信号经过调制之后传输过程中的SR现象,文献[12]研究了直接序列扩频信号在解调和解扩过程中的SR现象;而在信道编码方面,文献[13]采用串行级联turbo码通过单阈值比较器,引入噪声,来研究噪声对误码率的影响。文献[14]采用了并行级联turbo码,研究信号通过阈值阵列系统时,接收端经过译码之后,噪声对系统译码性能的影响。
本文在文献[14]的基础之上研究了信号经过网格编码调制[15-16](Trellis Coded Modulation,TCM)编码后通过阈值阵列系统时,噪声对信号译码接收性能的影响。TCM码将编码和调制相结合形成一个整体,它利用状态记忆和适当的映射来增大码字序列之间的距离。本文采用卷积码与8ASK调制相结合的编码方式,利用与文献[14]不同的阈值阵列系统作为解调器。此阈值系统由并行的多阈值系统单元构成[17]。
1 TCM编译码系统

图1TCM编译码流程图
Fig.1TheflowchartofTCMCodinganddecodingsystem
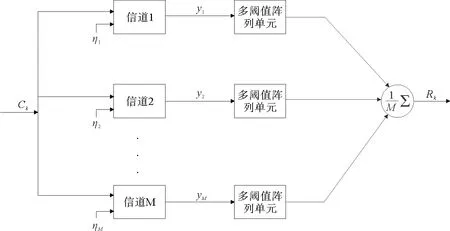
图2 阈值阵列系统Fig.2 Threshold array system
TCM编译码流程图如图1;阈值阵列系统的具体结构如图2所示。
信源S是随机产生的由0和1所组成的序列,经过TCM编码之后输出长度为n的已调信号序列C(c1,c2,…,cn),序列C经过阈值阵列系统之后输出序列R,在经由维特比译码之后得到D。本文TCM编码采用的是卷积码和8ASK调制相结合的设计,所以任意一个已调信号ck取值为{-7,-5-3,-1,1,3,5,7},其中k取值为{1,2,3,…,n},与之相对应的阈值阵列系统输出信号为Rk。
1.1 TCM编码
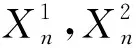
(1)
将码字映射为调制信号,此时不再是简单的与8ASK星座图一一对应,必须考虑卷积码状态转移规律。根据文献[16]提出的分集原理,得到图3的8ASK星座映射图,将码字与星座点一一对应,得到已调信号ck。通过公式(1),可知TCM编码部分可以看作是一个马尔科夫信源,公式(2)可以求出其各稳态分布概率[18],进而可以求出输出的已调信号为ck的概率P(ck)。公式(2)中Wi和Wj是稳态分布概率,pij是从i状态转移到j状态的一步状态转移概率。
(2)
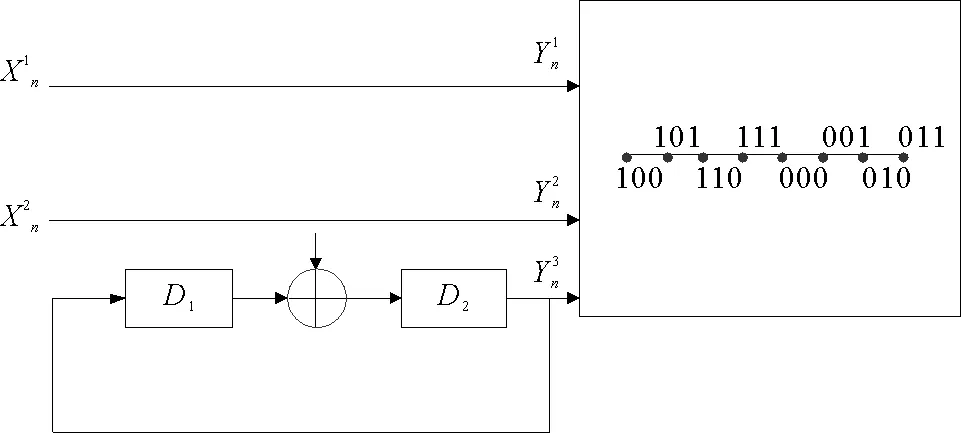
图3 TCM编码器结构Fig.3 The encoder structure of TCM
1.2 阈值阵列系统
图2给出了文中使用的阈值阵列系统结构,该阈值阵列系统有M个阈值阵列单元,每个阈值阵列单元是一个八阈值的多阈值模块。每个阈值阵列单元都具有相同的输入ck,同时也受到独立加性高斯白噪声的影响,每个阈值阵列单元的输出yi如公式(3)所示,其中n取值为{-5-3,-1,1,3,5},u是每个阈值单元阵列的阈值间隔。
(3)
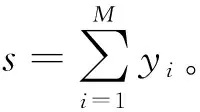
(4)

(5)
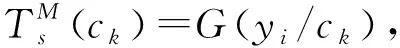
(6)
公式(6)同时是多阈值阵列系统在给定输入信号ck条件下输出求和取平均等于Rk的概率。
1.3 维特比译码
TCM编码是利用分集映射的方法增大最易混淆的信号之间的欧氏距离,从而获得更多的编码增益,所以,采用软判决的维特比译码[19]。译码的具体步骤如下:
1)将分支度量BM、路径度量PM、留存路径SUR等初始化为0,网格编码器初始状态设为00。
2)计算每个时刻每一个接收信号的分支度量BM即计算接收信号R与图3中每个信号的星座图之间的欧氏距离。更新各状态的路径度量,即将分支度量BM与前一时刻前一状态的路径度量PM相加。
3)比较延伸至同一时刻同一状态的路径度量PM,选择其中较小的,保存下来。同时记录此路径所对应的状态值,以方便可以正确地恢复原始信号。
4)重复使用上述方法,直到最后一个时刻,此时记录下来的路径就是最似然的路径,即与正确路径最接近的路径,然后根据记录下的历史状态进行译码,恢复出发送序列。
2 随机共振现象分析
文中分别通过互信息和误码率两个测度对信号通过阈值阵列系统时的变化情况进行了衡量。信道编码在信息论的基础上发展的,因此可以用互信息和误码率对信道编码的信号优劣进行衡量。
2.1 互信息测度的随机共振现象
通过计算阵列系统输出端信号Rk关于输入信号ck的互信息来研究信号的变化情况。互信息如公式7所示。
I=H(R)-H(R/C)
(7)
其中,

(8)
当噪声强度不为0时根据公式(5),(6),(7)可以计算出此时的互信息I。当噪声强度为0时,互信息I由公式(8)给出。综合公式(5),(6),(7),(8)可以计算出互信息I;且互信息只与阈值阵列间隔u、阈值阵列数M和噪声强度三者有关。图4和图5展示了互信息I受u,M和噪声强度影响下的变化情况。
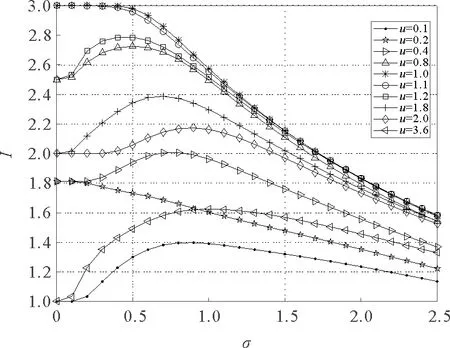
图4 M=3时在不同阈值单元阵列间隔u下互信息随噪声强度变化曲线图Fig.4 The variation of I with the noise intensity under different u when M=3
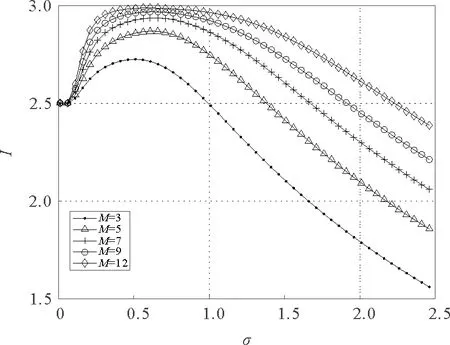
图5 u=0.8时在不同阈值阵列单元数M下互信息随噪声强度变化曲线图Fig.5 The variation of I with the noise intensity under different M for u=0.8
观察图4发现在固定阈值单元数等于3时,当u等于1.0或者1.1时即u在区间[5/6,7/6)未出现随机共振现象,这是因为当噪声强度为0时,互信息I达到了最大值3bit/符号,之后随着噪声强度增大互信息逐渐减小。当阈值间隔u不等于0.2,1,1.1时出现了随机共振现象,当噪声逐渐增大的时候,互信息I出现先增大后减小的变化趋势。表明在阈值阵列系统当中,适当的噪声会提高互信息I。此外,当u小于5/6时,随着u的增大,互信息的极值会逐渐增大,极值点会逐渐减小,当u大于等于7/6时,互信息的极值会随着u的增大而逐渐减小,极值点会逐渐增大。观察图5发现在不同阈值阵列单元数条件下都出现了随机共振现象,随着阈值阵列单元数M的增大互信息逐渐增大,且互信息的极值逐渐趋近于3bit/符号。当噪声强度趋近于0,互信息I趋近于一个确定的值,当噪声趋近于无穷大时,互信息趋近于0。
2.2 误码率测度的随机共振现象
利用MATLAB对整个系统进行仿真,来研究经TCM编码后的信号通过阈值阵列系统时,噪声对译码性能作用情况。仿真中采用先验概率为1/2的0、1随机序列,序列长度为107。仿真结果如图6和图7所示。
观察图6发现在以误码率为测度的情况下,阵列系统输出端信号变化出现了随机共振现象,表示当信号通过阈值阵列系统时添加适当的噪声会使得误码率得到一定程度的降低。当阈值阵列单元数逐渐增大时,这一现象更加明显,而当噪声强度趋近于0时,误码率趋近于一个确定的值,此时误码率与阈值阵列数几乎没有关系而只与阈值间隔有关。
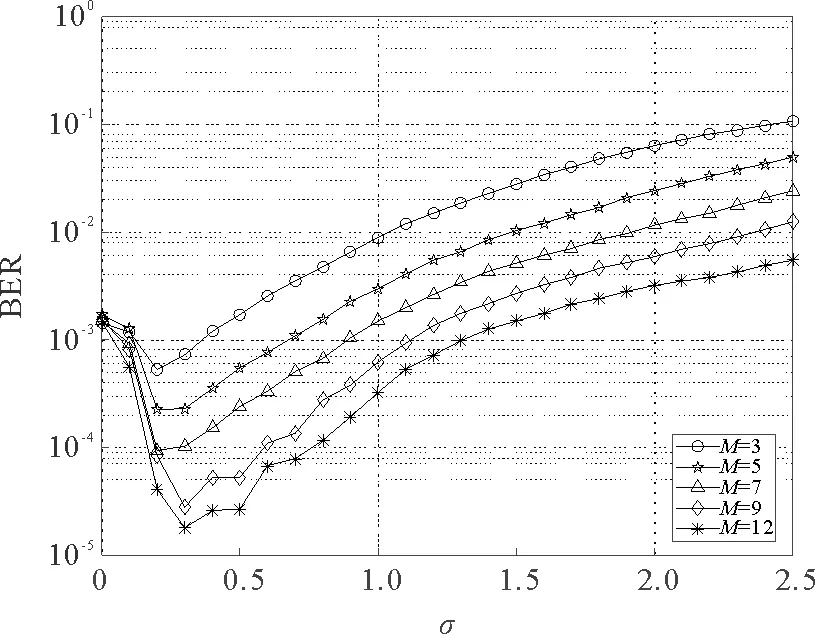
图6 u=0.8时不同阈值阵列单元数M下误码率随噪声强度的变化Fig.6 The variation of BER with the noise intensity under different threshold array element number M for u=0.8
观察图7发现当u不等于1.0、1.1、2.1或者2.2时,出现了随机共振现象,随着噪声强度的增加误码率出现了先减小后增大的变化。图7b中当u等于1.0或者1.1时未出现随机共振现象,这是因为,当多阈值阵列系统输出端在零噪声条件下,互信息已经达到最大值3bit/符号。图7a中u等于2.1或者2.2时未出现随机共振现象,是因为选用误码率作为测度导致未展现随机共振现象。

图7 M=3时不同阈值间隔误码率随噪声强度变化Fig.7 The BER of different threshold intervals varies with the noise intensity for M=3
3 两种测度下的随机共振现象对比

图8 u=0.8时不同阈值阵列数M下误码率随互信息变化曲线图Fig.8 The difference between BER and Mutual Information under different threshold arrays for u=0.8
本节对两种不同测度下的随机共振现象进行了对比。图8和图9分别展示了在不同阵列数和阈值间隔条件下随机共振现象的对比结果。观察图8发现在固定阈值阵列间隔u情况下,互信息出现先增大后减小的趋势,而误码率出现了先减小后增大的趋势,说明误码率和互信息都出现了随机共振现象,随着M的增加随机共振现象越加强烈,曲线的极小点逐渐趋近于点(0,3)。
观察图9a发现在阈值阵列单元数m等于3时,当u不等于0.2时,互信息是先增大后减小的,误码率出现了先减小后增大的趋势,这时误码率和互信息测度下都出现了随机共振现象,但是当u等于0.2时,互信息是一直减小的,而误码率是先减小后增大的,这表明此时在互信息测度下并未出现随机共振,而在误码率测度下出现了随机共振现象。事实上当u在区间[0.167,0.288]时都发生了这种情况。当u等于2.1或者2.2时互信息先增大后减小,而误码率一直增大,这表示在误码率测度下未出现随机共振,而在互信息测度下出现了随机共振。进一步研究发现当u在区间[2.1,2.4]时都出现此种情况。在文献[20]中以信噪比和误码率为测度的情况下也出现了不同测度下随机共振未一同出现的情况。图9的现象表明,随机共振现象是否出现与采用的测度标准有关。

图9 M=3时不同阈值间隔u下误码率随互信息变化Fig.9 The BER varies with mutual information under different threshold intervals for M=3
4 结语
文章主要研究了TCM编码后信号通过阈值阵列系统后,信号的变化情况。分别以互信息和误码率作为测度标准,进行了理论计算和仿真分析。当阵列数越多时,译码性能提高的越明显。不同的阈值阵列间隔会导致差异出现,当阈值阵列间隔在[2.1,2.4]时误码率未出现降低的现象而互信息出现了随机共振现象,当阈值阵列间隔处于[0.167,0.288]时误码率出现了随机共振现象,而互信息并未出现。综合以上研究结果表明,在使用多阈值阵列系统和维特比译码器相结合的系统时,通过引入适当的噪声、阈值阵列间隔和阵列数能够有效改善TCM编码信号的译码性能。这些研究结果对提高其他类型编码信号的抗干扰性有一定参考作用。另外,多阈值阵列系统仍需要进一步完善,例如阵列单元数的选取和阈值阵列间隔的选取,使译码性能达到预定要求。

