基于Triple Collocation方法的土壤湿度误差分析
吴 凯, 舒 红, 聂 磊, 焦振航
(武汉大学测绘遥感信息工程国家重点实验室,武汉 430079)
0 引言
土壤湿度是土壤的重要组成成分,通过改变陆地表面与大气间的物质和能量平衡而影响气候变化,是气象学、水文学等科学研究中的关键参数之一。常规的土壤湿度站点观测虽然精度高,但耗时费力且观测站点稀疏,获取的土壤湿度数据只能代表站点附近小范围的土壤湿度,空间代表性较差。随着遥感技术的快速发展,卫星遥感为获取大范围、长期实时的土壤湿度数据提供了有力的技术支持,具有速度快、效率高的特点。目前,全球尺度的土壤湿度来源主要是主动、被动微波遥感以及模型模拟。通过被动微波遥感中卫星亮温数据反演或主动微波遥感中后向散射系数处理可快速获取大范围的土壤湿度数据,但受观测仪器噪声和反演模型的不确定性影响而含有较大的误差。为了有效利用遥感土壤湿度数据,需要了解其观测误差大小,但现实中缺少大范围、长时间的土壤湿度真值,因而无法直接对遥感土壤湿度数据误差进行估计。
传统获取土壤湿度误差特征的方法依赖于卫星反演资料与地面实际观测的验证,但是该方法有3个缺点[1]: 一是土壤湿度地面站点观测被限制在有限的空间范围内,获取的土壤湿度数据时间范围有限,甚至因为仪器故障等原因而时间不连续; 二是由于遥感数据中代表性误差和尺度转换误差的存在使遥感土壤湿度误差估计复杂化; 三是该方法被限制在估计两个土壤湿度数据间的差异大小,不能同时得到两者的误差估计。误差估计的另一个方法依赖于土壤湿度反演模型与误差传播途径,通过模型输入数据的误差得到模型模拟土壤湿度的误差估计[2-3],其优点是可以得到每个独立观测数据的误差估计,但是该方法得到的土壤湿度不确定性只能解释模型输入变量中的随机误差,并不能说明模型本身是否正确,因此不同的反演模型得到的土壤湿度不确定性很难作定量化比较。
国外对遥感土壤湿度数据的误差分析研究取得了一定的进展。TC是1998年由Stoffelen最早应用于海洋学科评估风和浪高观测[4],后来被引入遥感土壤湿度观测误差估计和遥感土壤湿度数据同化误差方差计算中。K Scipal[5]等利用TRMM微波辐射计、主动微波散射计ERS-2土壤湿度反演数据和ERA-Interim土壤湿度再分析资料,采用TC方法得到3种数据各自的误差方差估计; K Scipal[1]等利用ASCAT,AMSR-E和ERA-Interim再分析资料,通过TC方法得到3个数据各自全球范围的误差估计,实验结果表明TC方法具有稳健性并能生成客观的误差估计; D J Leroux[6]等使用TC方法对SMOS,AMSR-E(LPRM)和ASCAT全球尺度的土壤湿度数据误差进行估计,分析比较了SMOS土壤湿度数据与已存在的土壤湿度数据间的差异; M Tugrul Yilmaz[7]等基于TC方法,使用ASCAT,AMSR-E土壤湿度反演数据和NOAH模型土壤湿度模拟数据,探讨了TC方法中土壤湿度误差与真值独立,以及三者土壤湿度误差间相互独立这两个前提假设对TC结果的影响,结果表明这两个假设导致TC结果被低估,土壤湿度误差间相互独立的假设比土壤湿度误差与真值独立的假设对结果有更大的影响; WA Dorigo[8]等探讨了TC方法中主被动微波遥感数据的选择、被动微波遥感不同频率(C波段、X波段和Ku波段)选择以及参考数据选择对结果的影响; L J Renzullo[9]等采用集合卡尔曼滤波的同化方法,利用AWRA-L模型模拟以及AMSR-E,ASCAT土壤湿度数据,使用TC方法估计了澳大利亚研究区域AMSR-E和ASCAT土壤湿度的误差方差并在土壤湿度数据同化中使用,获得了良好的同化结果。
本文首先对TC方法进行了推导,然后利用TC方法对研究区域内ASCAT,AMSR-E遥感反演土壤湿度数据及ERA-Interim土壤湿度再分析资料的误差方差和信噪比进行估计,并对TC结果进行了分析,通过MODIS土地覆盖类型数据分析了3种土壤湿度数据误差与土地覆盖类型的关系,并以此说明TC结果的合理性。
1 TC方法
假设对未知的土壤湿度真值θ有3个估计:θASCAT,θAMSR-E和θERA,分别表示ASCAT,AMSR-E和ERA-Interim土壤湿度数据,3种数据在时间和空间上整理排列后,使相同空间格网点、相同时间上3个土壤湿度数据均存在。TC方法有4个前提假设: ①3个数据集与真值间线性相关; ②误差稳定不随时间变化; ③3个数据集的误差相互独立; ④3个数据集的误差与真值独立。根据假设①可将3个数据表示为下列形式:

(1)
式中,εASCAT,εAMSR-E和εERA代表均值为0的加性噪声,根据假设③,εASCAT,εAMSR-E和εERA相互独立,即它们相互之间的协方差为0;αASCAT,αAMSR-E和αERA表示3组数据相对于真值θ的加性偏差系数;βASCAT、βAMSR-E和βERA表示3组数据相对于真值θ的乘性偏差系数。TC方法的目标是估计εASCAT,εAMSR-E和εERA的方差。
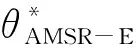
(2)
(3)
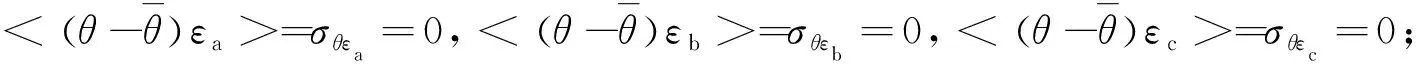
(4)
(5)
对上式两两做差相乘并取时间序列均值,得到式(6)。
(6)

(7)

求协方差法与做差法的不同之处在于无须事先选择参考数据以及对数据进行比例转换。真值θ和误差εi(i∈[ASCAT,AMSR-E,ERA])是2个随机变量,因此可以利用式(1)将观测数据的方差与协方差表示为
(8)
由前文假设(3)和(4)可将式(8)简化为
(9)
由上式可得最终结果,即
(10)
(11)
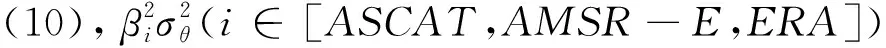
实验采用求协方差法估计研究区域内ASCAT,AMSR-E和ERA-Interim土壤湿度数据的误差方差和信噪比(signal to noise ratio, SNR),并使用式(12)将3个土壤湿度数据的信噪比(fMSE)标准化至[0,1],即

(12)
计算结果fMSE=0表示观测的土壤湿度信号无噪声,fMSE=1表示没有观测到任何土壤湿度信号,fMSE=0.5表示观测到的土壤湿度信号方差等于噪声方差。
做差法在式(2)中可以采取不同的线性变换方法(如最值变换法,累积概率分布函数匹配方法等[12]),因此做差法的求解结果不唯一。文献[10]中提到,做差法中使用式(2)中线性变换方法的求解结果与求协方差法的求解结果理论上是相同的,因此可将其他线性变换方法认为是TC方法中非最优的变换方法。
2 研究数据与方法
本文实验区域的位置为15°N~55°N,73°E~135°E,选取了2010年4月1日至2011年4月30日ASCAT,AMSR-E和ERA-Interim3种土壤湿度数据,ASCAT和AMSR-E土壤湿度的数值范围均为0~100,单位是百分数(%)。ERA-Interim土壤湿度单位是土壤体积含水量(mm3/mm3),将其采用最值线性变换的方法转换到百分数单位(%),即公式为
(13)
式中:ERAScaled为比例转换后的ERA土壤湿度,单位是百分数(%);ERA为原始的ERA土壤湿度数据,单位是体积含水量(mm3/mm3);ERAmax和ERAmin分别为ERA原始数据的最大值和最小值,两者的单位均为体积含水量(mm3/mm3)。
ASCAT(Advanced Scatterometer)搭载于Metop系列卫星上,是一个真实孔径的后向散射雷达,采用对土壤湿度较为敏感的C波段(5.3 GHz),从45°,90°和135°这3个方位角方向对每个观测点进行观测,得到连续的后向散射系数观测[13,14],通过TU-Wien发展的变化检测方法处理得到卫星过境时刻土壤表层(0~2 cm)的土壤湿度数据,空间分辨率为25 km。
AMSR-E(Advanced Microwave Scanning Radiometer Earth Observing System)是改进型的多频段、双极化的被动微波辐射计,搭载于AQUA卫星在2002年5月发射升空,分为上午星(降轨)和下午星(升轨)。实验中使用的是阿姆斯特丹自由大学和NASA共同研发的土壤湿度反演产品,含C波段和X波段两种土壤湿度估算产品,反演模型是LPRM模型[15]。由土壤发射的微波信号波长越小越容易被植被冠层吸收,与X波段相比C波段对土壤湿度更为敏感,因此实验选取了C波段土壤湿度数据[8],空间分辨率为0.25°。需要注意的是,反演产品中除土壤湿度外还有植被含水量估计,实验中使用的AMSR-E数据是指地表0~1 cm的土壤湿度,不包含地表上层植被含水量。
ERA-Interim是欧洲中期天气预报中心第三代再分析资料,提供自1979年以来的全球再分析资料,并实时更新。与第二代ERA-40再分析资料的数据同化模型相比,ERA-Interim采用了四维变分分析(4D-Var),同化了包括浮标、卫星高度计等数据在内的大量观测数据,实现了再分析资料质量的提升[16]。其土壤湿度数据将土壤分为4层,分别为[0,7) cm,[7,28) cm,[28,100) cm和[100,289] cm,实验中选取了ERA表层0~7 cm的土壤湿度数据。
实验中ERA、ASCAT和AMSR-E的土壤湿度的观测深度并不一致,虽然卫星遥感数据只能反映表层几厘米的土壤湿度,但是表层土壤湿度与0~10 cm的土壤湿度通常有密切的关系[17,18]。实验中认为表层10 cm之内的土壤湿度垂直变异不大,三者的土壤深度近似视为同一土壤深度。
MODIS卫星产品数据——MOD12Q1通过处理全年的Terra和Aqua观测数据得到土地覆盖类型数据,采用监督决策树分类方法将全球土地分为17种覆盖类型[19]。实验中选取了2010年MODIS土地覆盖类型数据(见图1),为了与TC结果进行比对,将其空间分辨率重采样至0.25°。实验中为确保TC结果可靠性,对3组数据间相关性低(相关系数小于0.2)的地区不进行处理,处理的网格点表示该地3组数据间的相关系数大于0.2且通过了相关系数的显著性检验(显著性α=0.05),对实验区域中的水体部分不使用TC方法进行计算。
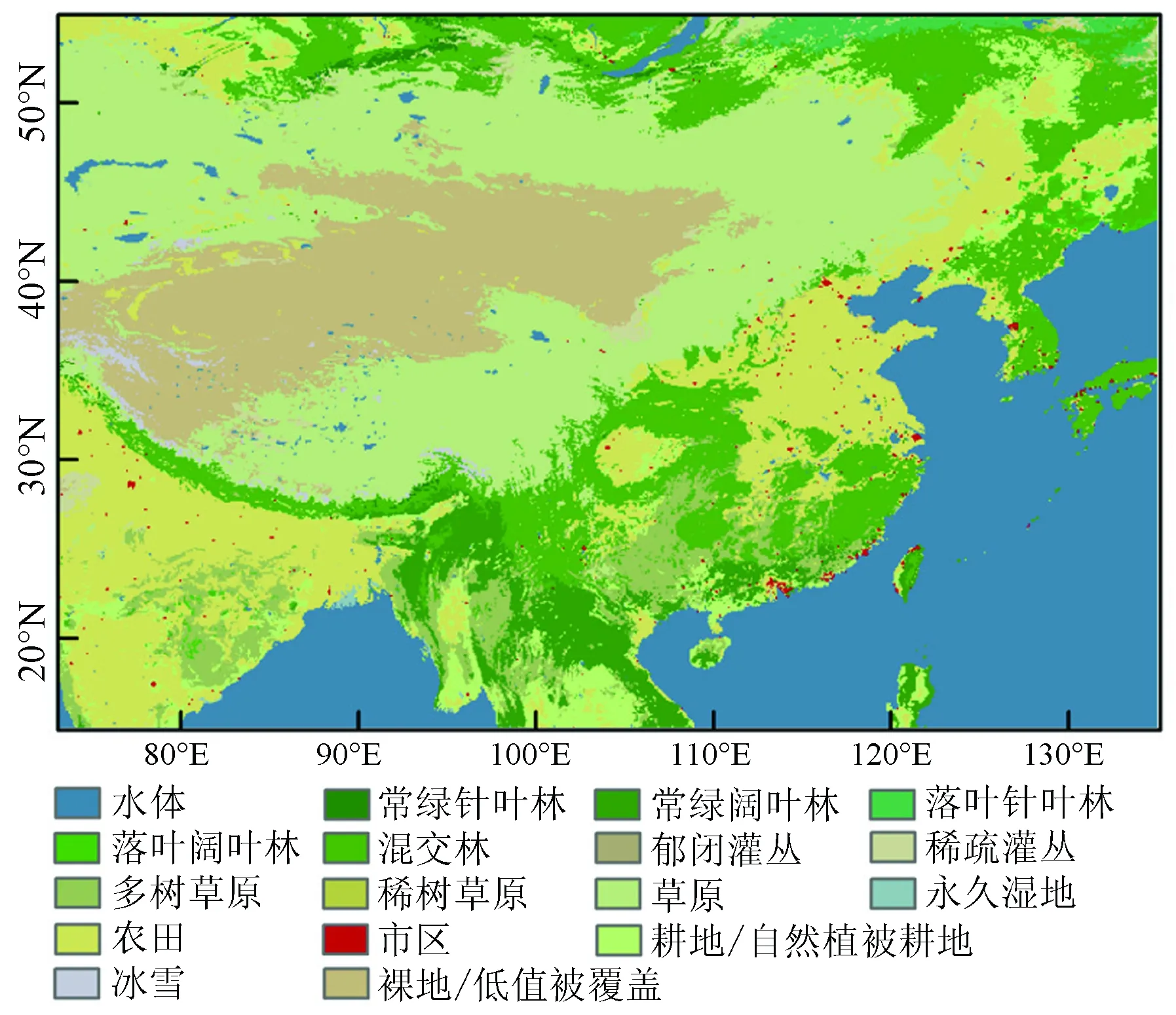
图1 2010年研究区域MODIS土地覆盖类型Fig.1 2010 MODIS land cover type classification in study area
3 结果与分析
根据ASCAT,AMSR-E和ERA土壤湿度数据间的相关性判断是否对该地使用TC方法估计其误差方差和信噪比,因此首先分析了3种土壤湿度数据间的相关性。图2表示研究区域ASCAT,ERA和AMSR-E这3种土壤湿度数据相互间的相关系数。

(a) 研究区ASCAT与AMSR-E土壤湿度相关系数 (b) 研究区ERA与AMSR-E土壤湿度相关系数 (c) 研究区ERA与ASCAT土壤湿度相关系数
图2研究区ERA,ASCAT及AMSR-E土壤湿度数据间相关系数
Fig.2CorrelationcoefficientbetweenASCAT,AMSR-EandERAsoilmoistureinstudyarea
可以看到ASCAT和AMSR-E在中国中部、新疆塔里木盆地和南部沿海区域土壤湿度的相关性差,在中国的青藏高原和印度的德干高原地区两者具有较高的相关性,研究区北部蒙古国地区两者的相关性也较好。ERA和AMSR-E土壤湿度在在中国中部、东南沿海以及研究区北部俄罗斯地区的相关性低,在其他地区的相关性较好。ERA和ASCAT土壤湿度在中国东南部以及中部地区相关性较高,在研究区北部俄罗斯和蒙古国地区、中国西北地区的相关性差,如中国新疆塔里木盆地的相关性甚至为负。
图3(a)(c)(e)分别表示研究区ERA、ASCAT和AMSR-E土壤湿度误差σ的空间分布,单位是百分数(%),(b)(d)(f)分别是其对应的直方图。(a)(c)(e)空白区域表示3组土壤湿度数据相互间的相关性较差(小于0.2)或无数据,有值表示3种数据的相关性均大于0.2且通过了α=0.05的相关系数显著性检验。
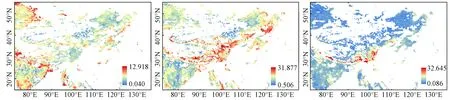
(a) ERA土壤湿度误差标准差的空间分布(b) ASCAT土壤湿度误差标准差的空间分布 (c) AMSR-E土壤湿度误差标准差的空间分布

(d) ERA土壤湿度误差标准差的直方图 (e) ASCAT土壤湿度误差标准差的直方图 (f) AMSR-E土壤湿度误差标准差的直方图
表1是ERA,ASCAT和AMSR-E土壤湿度误差的正态分布参数及置信区间估计(α=0.05)。3者的直方图显示3个土壤湿度数据的误差均呈现出正态分布的特征,由表1知ERA土壤湿度精度最高,其土壤湿度误差均值和方差是3者中最小的。AMSR-E土壤湿度精度低于ERA高于ASCAT,ASCAT土壤湿度误差最高,均值达到了12.728 9%,需要注意的是,这里的比较是依据TC结果判断的,TC结果并没有覆盖研究区全部,无法说明没有TC结果的地区3种土壤湿度的精度也是如此。由图3(a)(c)(e)3种土壤湿度误差σ的空间分布来看,3种土壤湿度数据在中国东南、中部地区和东南亚地区较少有TC结果分布,这些地区植被生长比较茂盛,导致ASCAT和AMSR-E遥感观测有较大误差,使得两者土壤湿度数据间的相关性很低。ERA土壤湿度误差在中国内蒙古高原和四川盆地、蒙古国东部较小,土壤湿度精度较高。ASCAT土壤湿度误差较大值主要分布在中国自青藏高原东南部,沿四川盆地西部、甘南、晋北一线直至沈阳的大片地区。AMSR-E土壤湿度误差在中国青藏高原南部边缘至四川盆地西北部地区的误差较高,达到了30%,此处的土地覆盖类型多为混交林; 与之相比,该地区两侧土地覆盖类型是农田、裸地和草原,误差则明显要小得多。图4(a)(b)(c)分别表示研究区ERA、ASCAT和AMSR-E经标准化的土壤湿度信噪比fMSE的空间分布,(d)(e)(f)表示它们对应的直方图。
(a) ERA土壤湿度fMSE的空间分布 (b) ASCAT土壤湿度fMSE的空间分布(c) AMSR-E土壤湿度fMSE的空间分布

(d) ERA土壤湿度fMSE的直方图 (e) ASCAT土壤湿度fMSE的直方图(f) AMSR-E土壤湿度fMSE的直方图
图4研究区ERA,ASCAT和AMSR-E土壤湿度fMSE空间分布及对应的直方图
Fig.4fMSEspatialdistributionsofERA,ASCAT,AMSR-Esoilmoistureandcorrespondinghistogramsinstudyarea
由图4可知3种土壤湿度数据的fMSE绝大部分数值较小,这说明观测信号中噪声信息较少。ASCAT土壤湿度的fMSE最小,说明其信噪比最高,除了在中国内蒙古高原西部和蒙古国中部地区的fMSE值较高外,ASCAT在其他地区的fMSE的值都普遍较低。ERA的fMSE高值集中在沿海地区,如中国渤海湾和山东半岛南部沿海地区、印度的德干高原东部沿海区,有的甚至达到了0.998,说明这些地区观测信号中掺杂了比例很高的噪声,这可能是ERA再分析资料处理海洋—陆地交界处的土壤湿度过程中由重采样等过程因素造成的。AMSR-E土壤湿度的fMSE较大值空间分布较为分散,仍可观察到中国内蒙古高原西部、松嫩平原附近以及泰国、老挝少部分地区fMSE值较高。
ASCAT是微波散射计,以主动方式发射连续的或脉冲形式的电磁波并接受散射回波, 而AMSR-E是微波辐射计,以被动方式接收来自地物目标的电磁辐射,虽然两者接受的观测信号中均会有地表覆盖植被电磁辐射的噪声影响,但是从理论上讲ASCAT比AMSR-E观测到更多的地物目标信息,因此ASCAT的信噪比理论上讲应比AMSR-E高,这与实验结果是相符的。

表2 土地覆盖类型与ERA,ASCAT和AMSR-E土壤湿度误差σTab.2 Land cover type classification and σ of ERA, ASCAT, AMSR-E soil moisture error
①Q1指较小四分位数,Q3指较大四分位数,min指数据最小值,max指数据最大值。
表2表示ERA,ASCAT和AMSR-E这3种土壤湿度数据误差σ与土地覆盖类型的数量关系。在微波遥感中,地表土壤的上行微波辐射会被覆盖的植被层衰减,植被层自身也有微波辐射,这些因素会影响观测到的土壤湿度信息。从表中可以看到,TC方法计算结果多分布在草原、农田和裸地,裸地植被覆盖率低,较少有植被辐射噪声,因此表2显示ASCAT和AMSR-E数据在裸地/低植被覆盖地区的土壤湿度误差较小,集中在0~Q3,且0~Q1范围内误差的数量占较大比例,较大四分位数Q3以上的误差所占比例很低。农田和草原虽然有植物覆盖,微波可以穿透,但仍会对土壤湿度观测有一定的影响,因此ASCAT和AMSR-E数据在农田和草地的土壤湿度误差比裸地的土壤湿度误差大,集中在Q1~Q3。对于植被覆盖茂密区域,如常绿阔叶林和混交林,ASCAT和AMSR-E的TC结果少,误差较大,集中在最大四分位数以上。ERA是再分析数据,对于不同的土地覆盖类型其土壤湿度误差大部分集中在Q1~Q2。通过上述分析可以发现TC实验结果比较符合实际情况,3种土壤湿度数据可以通过TC方法生成比较客观真实的误差方差估计。
4 结论
本文基于TC方法,使用ERA-Interim土壤湿度再分析资料、ASCAT和AMSR-E土壤湿度反演数据得到研究区域(15°N~55°N,73°E~135°E)内3种土壤湿度数据的误差方差和信噪比估计,结合MODIS土地覆盖类型数据对3种土壤湿度数据的误差方差进行了分析,主要结论如下:
1)植被覆盖会影响遥感土壤湿度的TC误差方差估计。研究区内东南亚、中国东南和中部地区植被覆盖较为茂盛,导致土壤湿度遥感观测具有较大误差,3种土壤湿度间的相关性较差,致使TC方法无法准确估计这些地区的土壤湿度误差方差和信噪比。
2)从TC误差方差估计值来看,ERA土壤湿度误差的均值和方差最低,精度最高, AMSR-E土壤湿度精度低于ERA高于ASCAT,ASCAT土壤湿度数据精度最低。但需要注意的是,这里的比较是依据TC结果判断的,TC结果并没有覆盖全部研究区域。
3)TC方法得到的3种土壤湿度数据的fMSE均较小,这表明ERA,ASCAT和AMSR-E土壤湿度观测数据中噪声所占比例很低。从观测到的信号来看,ASCAT的fMSE值相对较低,信噪比最高; ERA的fMSE高于ASCAT低于AMSR-E,ERA土壤湿度的fMSE高值集中在海洋—陆地交界区域,这可能是ERA再分析资料重采样等过程因素造成的; AMSR-E的信噪比最低,观测信号中噪声相对ASCAT和ERA来说较高。主动微波ASCAT从理论上讲信噪比高于被动微波AMSR-E,与实验结果一致。
4)通过MODIS土地覆盖类型数据与TC结果的分析可知,TC方法得到的研究区域土壤湿度误差估计多分布在草原、农田和裸地,TC方法能够得到较为真实客观的土壤湿度误差方差估计。
需要注意的是,本实验中3种土壤湿度数据的观测深度以及观测时间并不完全一致,这会对实验结果有一定影响; TC方法假设观测误差在一定时间内是恒定的,这并不符合实际的情况; TC方法以每个像元为处理单元,这就表示TC方法的土壤湿度误差方差估计结果没有考虑不同像元土壤湿度的空间相关性。如何对TC方法中这些缺陷进行改进是我们下一步的工作内容。

