节流孔式空气阻尼系统建模及参数影响分析

陈俊杰， 殷智宏， 郭孔辉， 何江华， 曾祥坤， 袁显举

(1. 江西理工大学 机电工程学院，江西 赣州 341000； 2.华南理工大学 机械与汽车工程学院，广州 510640； 3.广州溢滔钱潮减震科技股份有限公司，广州 510540； 4.吉林大学 汽车工程学院，长春 130025； 5.广东技术师范学院 汽车学院，广州 510635； 6.湖北汽车工业学院 汽车学院，湖北 十堰 442002)

空气弹簧质量轻、摩擦小，能有效降低簧下质量和轮胎动载荷，降低振动、噪声，具有良好的道路友好性和优越的乘坐舒适性，已广泛在火车、客车、货车、豪华轿车和SUV上应用。随着空气弹簧在列车和汽车领域中应用越来越广泛，对空气弹簧进行理论研究也越来越受到了各国学者和工程技术人员的重视。Benjamin[1]首次提出并研究了空气弹簧的有效作用面积，设计了一种膜式空气弹簧，并针对空气弹簧的有效作用面积特性进行了一系列的实验研究。喻凡等[2]建立了空气弹簧垂向特性模型，并通过实验研究了在大频率和大幅值情况下空气弹簧的侧向特性。Fox等[3]对膜式空气弹簧的静刚度特性进行了较为深入地研究，对有效面积进行了等效处理，提出了由压缩空气模型、Fancher迭代摩擦模型和速率相关的阻尼模型并联而成的空气弹簧模型。

上述研究仅针对单个工作气室的空气弹簧，这种单气囊空气弹簧设计完成后刚度不能根据路况进行调节，也没有阻尼作用，需要采用传统的液压减振器或阻尼可调减振器衰减振动。尽管阻尼连续可调减振器大大提高了汽车悬架系统的性能，但其重量增加了簧下质量，同时也存在油液泄漏的问题。故一些学者开始通过引入附加气室和节流孔构成节流孔式空气阻尼系统，实现空气阻尼，以达到减振隔振的目的。该系统在引入空气阻尼的同时其刚度特性也发生了变化，因此必须对节流孔式空气阻尼系统的刚度和阻尼特性进行研究，为合理设计和应用空气阻尼衰减振动提供理论依据。

为了研究节流孔式空气阻尼系统的动力学特性，国内外学者进行了大量研究。1957年，在郭孔辉院士的领导下，第一机械工业部长春汽车研究所和化工部橡胶工业研究所联合研制了我国第一款重型汽车空气弹簧，对空气弹簧进行了大量的试验工作[4]。Yin等[5-6]建立了气缸式空气阻尼系统的非线性模型，并在平衡点附近进行了线性化处理，得到了该系统的等效阻尼系数比模型，提出了一种便于进行空气阻尼设计的空气阻尼图表；并在此研究的基础上，基于公理设计理论，设计了一种用于汽车的新型空气悬架，该空气悬架实现了高度和刚度调节的解耦。王家胜等[7]对节流孔式空气阻尼悬架模型进行了线性化处理，得到了系统动刚度的线性化模型，分析了影响系统动刚度的影响因素。Toyoufuku等[8]研究了带附加气室空气悬架的电磁阀和设计参数对空气弹簧刚度特性的影响，该设计在1997年已成功应用在五十铃观光巴士上，该空气悬架由空气弹簧、附加气室、连接管路和开关电磁阀等组成，利用开关电磁阀切断和连接空气弹簧和附加气室，起到改变容积，实现空气悬架刚度调节的功能，但是在高频激励下，由于空气弹簧的压力变化不能及时通过管路传递到附加气室，导致刚度调节失效。Soleiman等[9]通过在空气弹簧和附加气室之间引入连接管进行节流，产生阻尼，并指出该阻尼作用在低频时较大，在高频时较小，大大改善了隔振性能。但是该系统在低频时刚度较小，在高频时刚度较大，不利于提高乘坐舒适性。美国福特汽车公司的Bachrach等[10]在Soleiman的研究基础上，推导了用毛细管连接主气室和附加气室的空气弹簧的动刚度和耗能因数，分析发现附加气室和主气室的体积比是影响动刚度和耗能因数的关键因素，分析得出连接管的尺寸仅仅影响最大阻尼出现的频率，不影响最大阻尼值的大小。张广世等[11]利用气体热力学和流体力学理论推导了空气弹簧、连接管路和附加气室的空气阻尼式空气弹簧系统动力学模型，研究了连接管路的长短、管径大小以及管内气体质量对悬架性能的影响。贺亮等[12]以凡士通公司的1T15M-2型膜式空气弹簧为基础，构建节流孔空气阻尼式空气弹簧，采用单自由度自由衰减振动的方法，研究了不同气压下悬架的垂直刚度和阻尼随节流孔径变化的规律，得出在孔径为5 mm附近时阻尼达到最大值。潘孝斌等[13]将空气阻尼应用于高速弹体软回收，分析了弹体初速、气室初压和破膜压力之间的匹配关系，拓展了空气阻尼的应用领域。但上述研究都没有考虑空气弹簧橡胶气囊的力学特性，造成了实验数据和理论计算之间的较大差异；同时未深入研究设计参数对系统动态特性的影响，不便于进行车辆悬架的设计和匹配。

本文考虑空气弹簧橡胶气囊力学特性，首次采用摩擦模型和分数导数Kelvin-Voigt模型建立了橡胶气囊力学模型，并提出了橡胶气囊模型参数的识别方法。基于热力学、牛顿力学和流体力学理论建立节流孔式空气阻尼系统的非线性模型，在系统平衡点附近，对该系统模型进行了线性化处理，并基于复刚度等效推导了该系统的等效刚度和等效阻尼系数方程，实验验证了橡胶气囊模型和系统线性化模型的有效性。最后，分析了外部输入参数及系统设计参数对等效刚度和等效阻尼系数的影响规律，为进一步研究空气阻尼系统的刚度和阻尼设计、匹配提供了理论依据和有效参考。

本文所建立的橡胶气囊模型及其参数识别方法，进一步完善了空气弹簧的力学模型，大大降低了理论与实验数据之间的误差。基于复刚度等效得到的系统等效刚度和等效阻尼系数可直接用于空气阻尼悬架系统的匹配设计，更加直观和利于工程师进行悬架设计应用。关键设计参数对等效刚度和等效阻尼系数的影响规律研究为空气阻尼悬架系统的优化设计提供良好的理论依据。

1 节流孔式空气阻尼系统建模

节流孔式空气阻尼系统如图1所示，主要由空气弹簧主气室，附加气室，连接管路和节流孔组成。空气弹簧用于承受垂直载荷，其垂直向上的作用力包括压缩空气产生的作用力Fa和橡胶气囊的作用力Fb，F=Fa+Fb。其中，压缩空气产生的作用力Fa可表示为：

Fa=(Pz-Patm)Az

(1)

式中:Pz为主气室内气体绝对压力；Patm为大气压强；Az为空气弹簧有效工作面积;Az=Az0+β(zs-zu)，Az0为在标准工作高度(即系统工作平衡点)附近下空气弹簧有效工作面积;β为空气弹簧有效工作面积变化率;zs是簧上质量位移;zu是输入位移。

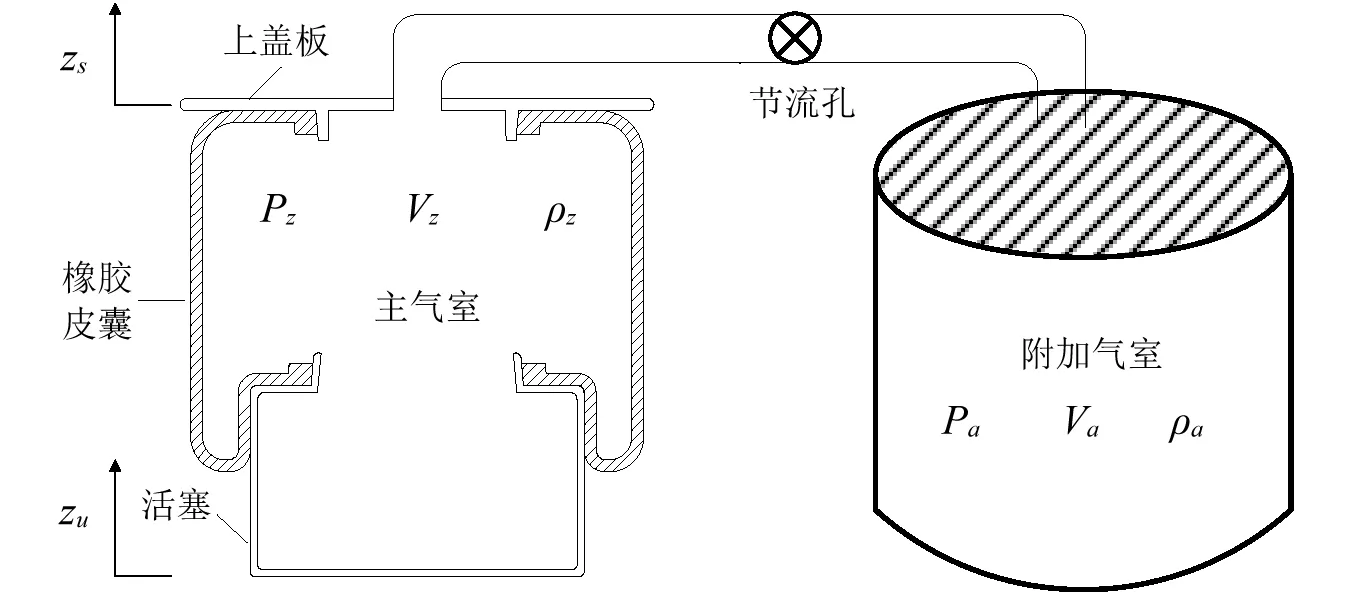
图1 节流孔式空气阻尼系统示意图Fig.1 Schematic diagram of OADS

1.1 橡胶气囊模型

空气弹簧橡胶气囊模型主要包括库仑摩擦模型和分数导数Kelvin-Voigt模型。库仑摩擦模型表征了橡胶气囊的振幅相关性，分数导数Kelvin-Voigt模型表征了橡胶气囊的频率相关性。

(1)库仑摩擦模型

图2 库仑摩擦模型Fig.2 Coulomb friction model

应用摩擦模型来描述橡胶气囊动态特性的振幅相关性，见图2，其力和位移的关系为[14]：

(2)

式中：Ffmax表示最大摩擦力；x2表示达到最大摩擦力一半所对应的位移大小；x0表示输入激励的振幅；Ffs和xs分别表征参考状态的初始力和初始位移；参量Δ=Ffs/Ffmax，Δ∈[-1,1]。摩擦模型的刚度和滞后角为：

(3)

(4)

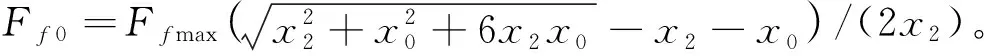
(2)分数导数Kelvin-Voigt模型

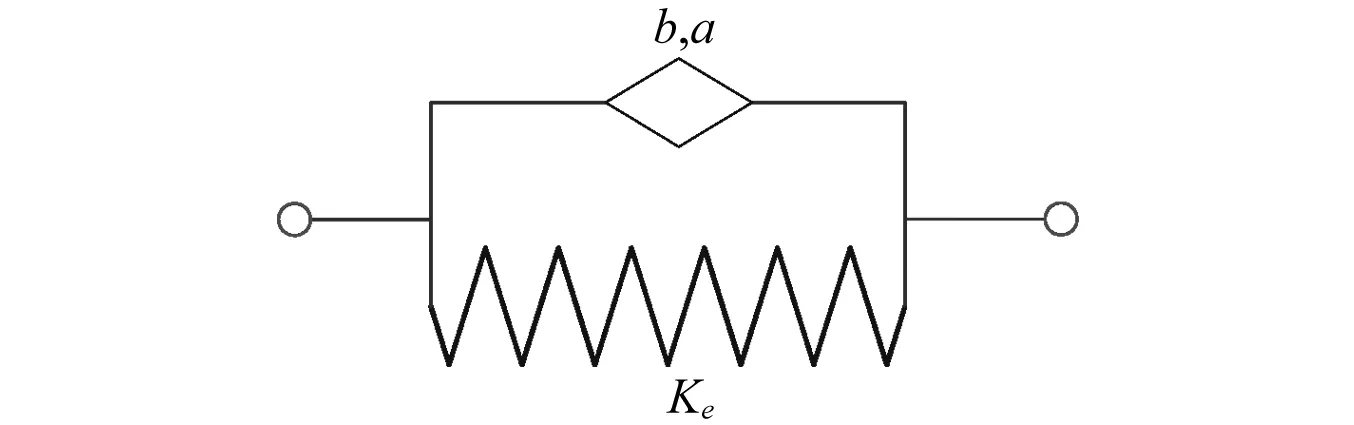
图3 分数导数Kelvin-Voigt模型Fig.3 Fractional derivative Kelvin-Voigt model

应用分数导数Kelvin-Voigt模型来描述橡胶气囊动态特性的频率相关性。采用分数导数描述的橡胶气囊的力与位移关系为[14-15]：

Fv(t)=Kex(t)+bDax(t)

(5)

式中:Ke为线弹性刚度;a为分数导数阶次;b为分数导数阻尼参数;Fv(t)是黏弹性力；Dax(t)表示位移x(t)的a阶分数导数。对方程(5)进行傅里叶变换后，得到分数导数Kelvin-Voigt模型的动刚度和滞后角为：

(6)

(7)

1.2 主、附加气室模型

主气室中的压缩空气满足理想气体状态方程和绝热过程， 空气弹簧主气室和附加气室之间流动的气体满足质量流量连续性，由此可得到主气室内气体质量流量Gz与气体压强及体积变化关系为[16]：

(8)

式中:R为热力学常数；Pz0、Tz0分别为标准工作高度下主气室内气体初始绝对压力和初始温度；k为热力学多变指数；Vz为主气室容积，Vz=Vz0+α(zs-zu)，Vz0为在标准工作高度下空气弹簧有效工作容积，α为空气弹簧有效工作容积变化率。在系统平衡点附近，对主气室模型进行线性化：

(9)

式中:Tz0=T0，Pz0=P0。

由式(9)可见，在系统工作平衡点附近，主气室内气体压强变化率由主气室内气体质量流量和气体体积变化引起，且与二者成线性关系。

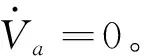
(10)

式中:Pa、Va分别为附加气室内气体绝对压力，容积；Pa0、Ta0分别为附加气室内气体初始绝对压力和初始温度。在系统工作平衡点附近，对附加气室模型进行线性化：

(11)

式中：Pa0=P0，Ta0=T0。由式(11)可见，附加气室气体压强变化率与气体质量流量成线性关系。

1.3 节流孔模型

系统工作时，流经节流孔的空气具有压缩性，其流量特性表现为非线性特性。节流孔在流量特性上可以等价为一个小孔。在平衡点附近，采用割线法对流经节流孔的气体质量流量变化Gz进行线性化，得到：

(12)

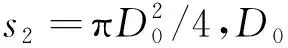
2 等效刚度和等效阻尼系数的计算方法

对方程式(1)、(9)、(11)和(12)进行拉普拉斯变换，并结合方程式(3)、(4)、(6)和(7)，得到系统的复刚度计算式为：

K(jω)=Kar+Kfcosφf+Kvcosφv+

j[Kai+Kfsinφf+Kvsinφv]

(13)

其中，

(14)

(15)

(16)

(17)

(18)

式中:Ks表示有效工作气体体积仅为空气弹簧主气室内气体时的体积刚度；Kd表示有效工作气体体积为空气弹簧主气室和附加气室体积之和时的体积刚度；KA为面积刚度；N为附加气室体积和主气室体积之比；Ca表示附加气室气容大小。

为了便于进行节流孔式空气阻尼系统刚度和阻尼的设计与匹配，将该系统等效成有阻尼的单自由度弹簧阻尼系统，见图4。

图4 等效弹簧阻尼系统Fig.4 The equivalent spring-damping system

图4中，等效弹簧阻尼系统复刚度为：

Keq(jω)=keq+jωceq

(19)

式中：Keq为等效复刚度;keq为等效刚度;ceq为等效阻尼系数。

对同一空气悬架系统，由于方程式(13)与(19)是等价的，可见，复刚度的实部表征悬架刚度，虚部表征悬架阻尼系数和频率的乘积。令ω0=1/(RfCa)，节流孔式空气阻尼系统等效刚度和等效阻尼系数为：

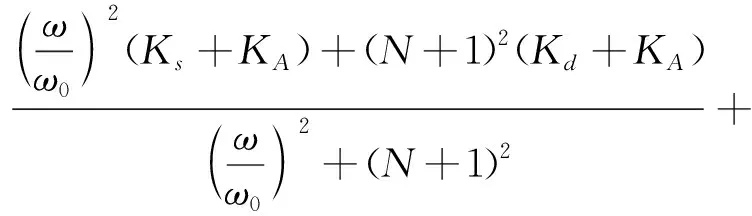
Kfcosφf+Kvcosφv

(20)

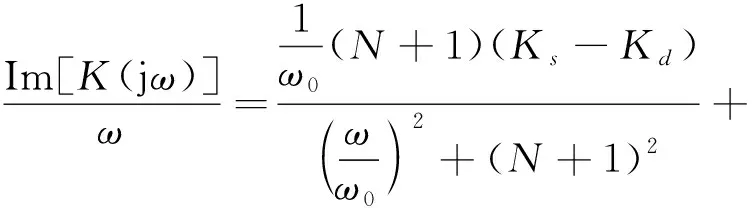
(21)

由方程式(20)、(21)可见，等效刚度和等效阻尼系数具有振幅相关性和频率相关性，并与孔径、体积比等系统设计参数有关。

3 实验验证

3.1 实验装置

文中以某空气弹簧(广州溢滔钱潮生产)作为研究对象，实验装置如图5所示，空气弹簧安装在MTS液压作动器和力传感器之间，空气弹簧主气室3、2.5 mm直径的节流孔7和附加气室9之间通过内径8 mm的硬质尼龙管连接。调压阀10用于控制充入空气弹簧主气室和附加气室的初始压强。

1-MTS设备 2-MTS液压作动器 3-1A975空气弹簧4-工装5-力传感器和加速度传感器 6-压强传感器 7-2.5 mm直径的节流孔 8-压强传感器 9-附加气室 10-调压阀及开关阀11-MTS液压站 12-储气罐 13-空气干燥器14-空气压缩机图5 节流孔式空气阻尼系统实验装置Fig.5 Test rig of OADS

3.2 橡胶气囊参数识别及模型验证

3.2.1橡胶气囊参数识别

橡胶气囊参数需要通过空气弹簧主气室的静、动刚度实验辨识得到。首先，为识别橡胶气囊的参数，将节流装置和附加气室移除，进行空气弹簧主气室的静刚度和动刚度实验。静刚度测试时，MTS试验台其液压作动器对主气室施加一个加载速度为10 mm/min，幅值分别为5 mm，10 mm和15 mm的三角波激励信号，静刚度实验时加载频率极低，橡胶气囊的黏弹性效应可以忽略，主气室的静刚度取决于库仑摩擦模型。主气室静刚度测试得到的迟滞回线如图6所示，采用振幅为5 mm的三角波激励信号所获得的迟滞回线可以识别出橡胶气囊模型中的线性刚度Ke, 最大摩擦力Ffmax和达到最大摩擦力一半时所对应的位移x2，这三个参数关系满足[15]：

(22)

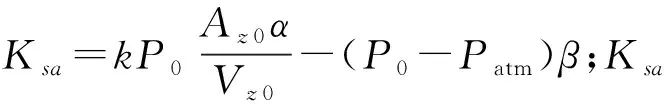
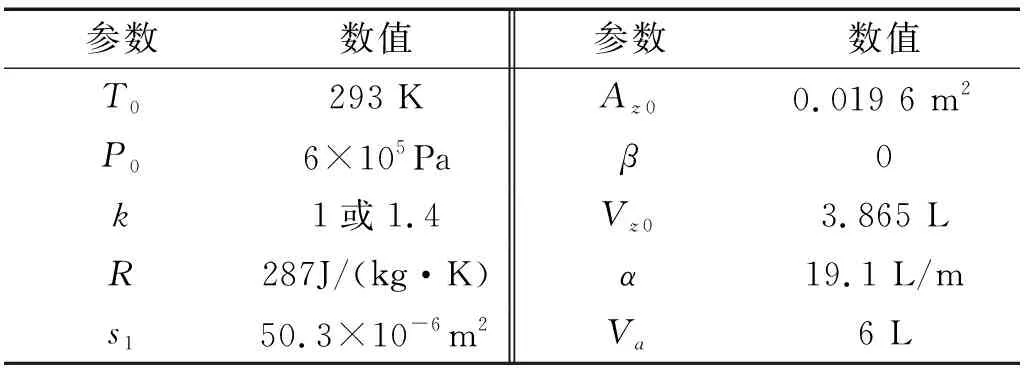
表1 主气室模型参数

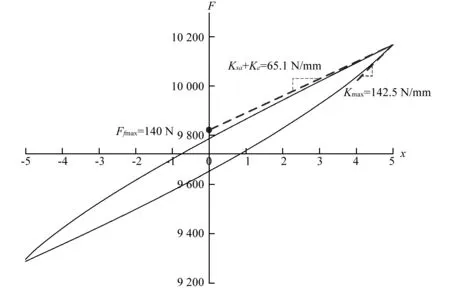
图6 主气室静刚度迟滞回线Fig.6 Hysteresis loop of the main chamber

主气室动刚度实验时，MTS液压作动器激励信号采用振幅分别为5 mm，10 mm和15 mm，频率为0.5～10 Hz，间隔0.5 Hz的正弦信号进行扫频。通过采用振幅为5 mm、频率为0.5～10 Hz，间隔0.5 Hz的正弦扫频信号获得的主气室的动刚度特性减去库仑摩擦模型和主气室压缩空气刚度的影响可得到分数导数Kelvin-Voigt模型在该激励信号下对单个空气弹簧动刚度特性的贡献值，采用最小二乘法拟合提取得到分数导数阶次a和阻尼参数b[17-18]。辨识得到的橡胶气囊参数见表2。

表2 橡胶气囊参数

3.2.2橡胶气囊模型验证

主气室静刚度迟滞回线和动刚度计算、实验结果对比见图7。由图7(a)可见，库仑摩擦模型可以准确地复现不同振幅下的迟滞环和尖角效应，且随着振幅的增大，静刚度减小。由图7(b)可见，橡胶气囊模型可以很好地描述不同振幅下的动刚度特性，随着振幅的增大，动刚度减小；随着频率的增大，动刚度逐渐增大。尽管橡胶气囊模型参数是仅仅通过振幅5 mm的静、动刚度实验所识别得到，但该模型能够很好地复现振幅分别为10 mm和15 mm时主气室的静刚度和动刚度特性，表明橡胶气囊模型是有效的。

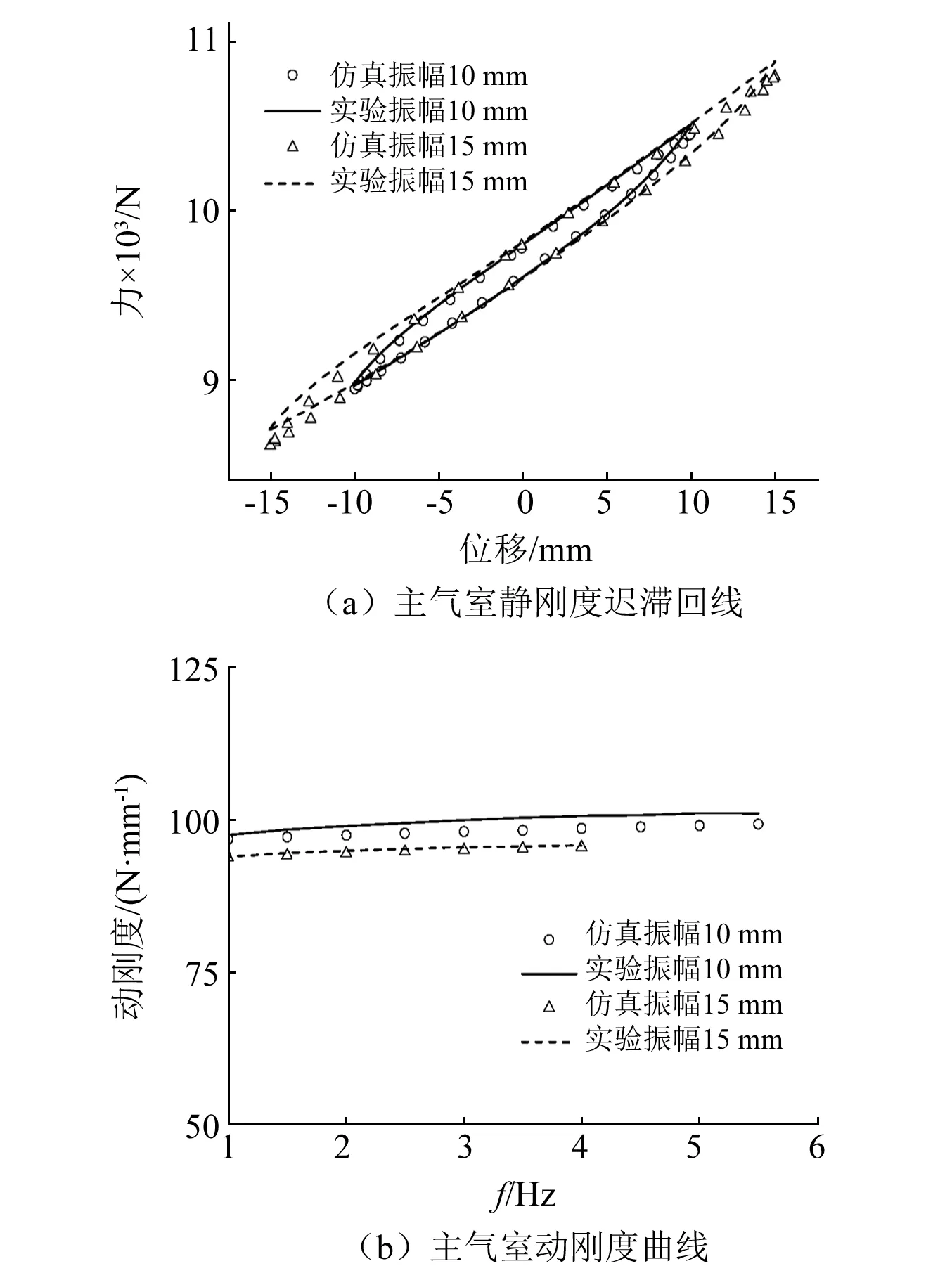
图7 主气室静、动刚度计算、实验结果对比图Fig.7 Comparison of calculation results and experimental data ofstatic stiffness and dynamic stiffness of the main chamber

3.3 节流孔式空气阻尼系统模型验证

最后，文中进行了节流孔式空气阻尼系统动刚度特性实验。动刚度特性实验时，MTS液压作动器对空气弹簧各分别施加振幅为10 mm和15 mm，频率为0.5～6 Hz，间隔0.5 Hz的正弦扫频激励信号。

孔径为2.5 mm的空气阻尼系统等效刚度和等效阻尼系数计算值和实验结果对比图见图8。由图8可见，该系统等效刚度和等效阻尼系数计算和实验结果吻合较好，说明文中所建立的节流孔式空气阻尼系统模型可用于表征在一定激振振幅和激振频率下系统的刚度、阻尼特性。

图8 节流孔式空气阻尼系统等效刚度和等效阻尼系数计算、实验结果对比图Fig.8 Comparison of calculation results and experimental data ofequivalent stiffness and equivalent damping coefficient of OADS

4 参数影响分析

为进一步研究节流孔式空气阻尼系统等效刚度和等效阻尼系数特性，文中针对激振振幅、激振频率和关键设计参数对等效刚度和等效阻尼系数的影响规律进行详细分析。

4.1 激振振幅和激振频率影响分析

节流孔径为2.5 mm，在振幅分别为5 mm、10 mm和15 mm的三种扫频正弦激励下系统的等效刚度和等效阻尼系数计算结果见图9。由图9可见，等效刚度和等效阻尼系数都具有振幅相关性和频率相关性。等效刚度随频率的增大逐渐由下边界过渡到上边界，呈拉平的S曲线状；等效阻尼系数随频率增大逐渐减小，呈反S曲线状。由于空气弹簧橡胶气囊的振幅相关特性，振幅的增大导致等效刚度下降；且使中间过渡频段变窄，等效刚度值从下边界到上边界的上升速度较快，这主要是振幅的增加提高了流经节流孔的气流速度，加快了空气弹簧主气室和附加气室的隔绝。当频率很低时，等效刚度处于下边界，此时主气室和附加气室无障碍相通；当频率很高时，等效刚度处于上边界，空气弹簧主气室内气压变化没有时间传递到附加气室，空气弹簧主气室和附加气室隔绝。等效阻尼系数随频率的增加而迅速降低，当频率增大到一定程度时，阻尼很小且接近零，此时主气室和附加气室隔绝，节流阀无气流通过，不产生阻尼作用。当振幅增大时，等效阻尼系数随频率呈现先增加后减小的趋势，在低频段，振幅的增大有利于提高气流通过节流孔的速度，增大阻尼且阻尼峰值左移；在高频段，振幅的增大加速了气流通过节流孔时产生壅塞现象，加速了主、附气室的隔绝，降低了阻尼。

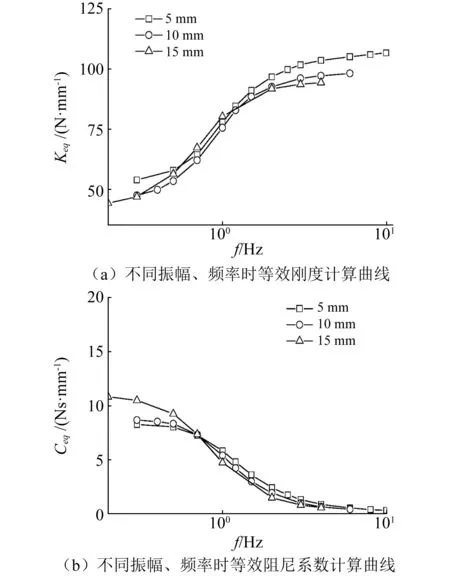
图9 不同激振振幅和激振频率时系统等效刚度和等效阻尼系数计算结果Fig.9 Calculation results of equivalent stiffness and equivalentdamping coefficient of OADS at different excitation amplitudesand excitation frequencies

4.2 节流孔径影响分析

振幅为10 mm、不同孔径时系统等效刚度和等效阻尼系数计算结果见图10。从图10可见，孔径大小不影响等效刚度的上边界值和下边界值。更大的节流孔径降低了气流通过节流孔的速度，导致等效刚度曲线右移，中间过渡频段变宽；同时孔径的增大也导致低频段等效阻尼系数大大降低，而在高频段，大的孔径产生略大的等效阻尼系数，此后随着频率增大，阻尼逐渐减小至接近零。因此，改变节流孔径可以明显改变空气悬架的刚度过渡特性和阻尼大小，相对小的孔径可以获得更大的阻尼和更快的刚度过渡特性。

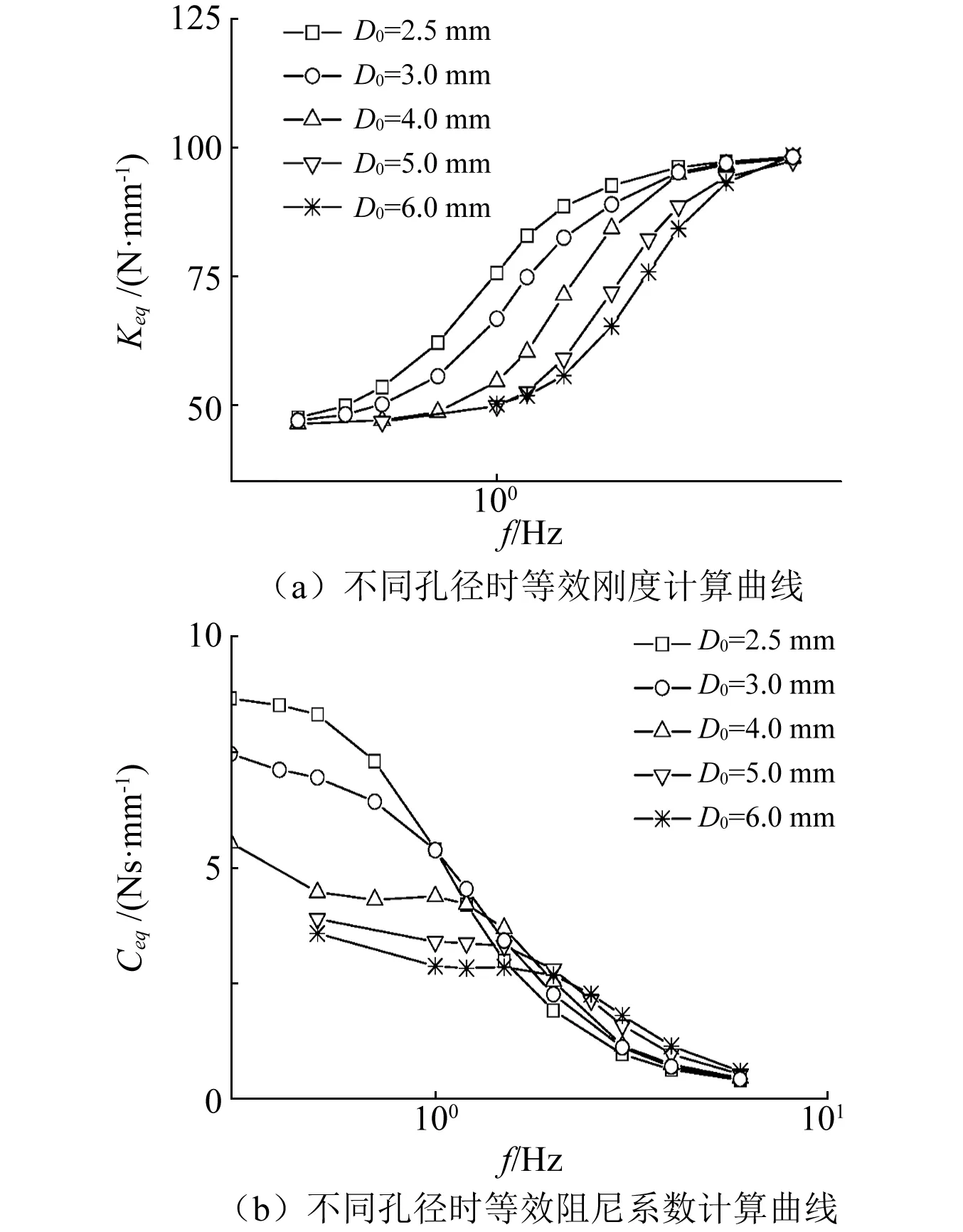
图10 不同孔径时系统等效刚度和等效阻尼系数计算结果Fig.10 Calculation results of equivalent stiffness and equivalentdamping coefficient of OADS with different orifice diameters

4.3 附加气室和空气弹簧主气室体积比影响分析

孔径为2.5 mm、振幅为10 mm、不同体积比时系统等效刚度和等效阻尼系数计算结果见图11。由图11可见，较大的体积比使等效刚度和等效阻尼系数的变化范围增加。体积比的增大降低了等效刚度，使等效刚度值从下边界到上边界的上升速度加快，但不改变等效刚度的上边界值。较大的体积比可以获得更大的等效阻尼系数，有利于衰减振动。但当体积比增加到一定程度(图中为N=5)时，体积比对系统等效刚度和等效阻尼系数的影响作用明显减弱。总体而言，体积比决定了刚度变化范围的大小，较大的体积比可得到较软的刚度特性；体积比的增大有利于提高系统阻尼。在悬架布置空间允许的情况下，通过增加附加气室体积可以得到更柔软的悬架刚度特性和更大的悬架阻尼，有利于提高车辆的乘适性。

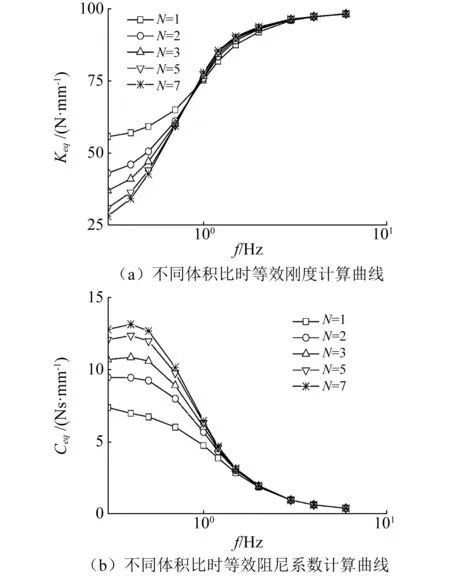
图11 不同体积比时系统等效刚度和等效阻尼系数计算结果Fig.11 Calculation results of equivalent stiffness and equivalentdamping coefficient of OADS with different volume ratios

5 结 论

(1)首次引入分数导数Kelvin-Voigt模型和摩擦模型对空气弹簧橡胶气囊力学特性进行建模，提出了橡胶气囊模型参数的识别方法，实验验证了模型的准确性，进一步完善了空气弹簧的力学模型。

(2)在系统工作平衡点附近，建立了节流孔式空气阻尼系统线性模型，基于复刚度推导了节流孔式空气阻尼系统等效刚度和等效阻尼系数方程，实验验证了线性模型的有效性。

(3)最后，分析了激振振幅、激振频率、节流孔径大小和体积比对系统的等效刚度和等效阻尼系数的影响规律，对进一步研究空气阻尼悬架的刚度和阻尼设计、匹配提供了理论依据，具有实际工程价值。