有限幅波理论下小水线面双体船非线性波激振动研究

唐宇航， 陈志坚

(1. 中国人民解放军92578部队，北京 100161； 2. 海军工程大学 舰船工程系，武汉 430033)

船舶在较平稳的波浪中航行时出现显著的持续总振动现象，称之为波激振动[1]。目前，关于波激振动的描述有线性和非线性之分，导致非线性波激振动原因有很多，一般人们认为是船-波间遭遇频率与总振动频率存在倍频关系[2]以及其他非线性激励所致，例如船舶剖面水线宽、附加质量以及水动力阻尼等引起的非线性效应[3]。

海浪是海洋环境中最为复杂的自然现象，可分为长峰波和短峰波。波浪对船舶的扰动可分为一阶力和二阶力[4]，海洋工程结构受到的非线性波浪载荷也一直是人们关注的重点，其主要是对二阶波浪力的研究[5-6]。微幅波作为有限幅波的一阶近似，是描述线性波激振动常用波形；高阶有限幅波理论可以对波浪的高阶成分进行描述，也称之为斯托克斯波，可以独立于船型有效地解释船舶在波浪航行中产生高阶振动激励力的来源。

美国学者曾经对线性和非线性波激振动的重要性进行了论述，发现某305 m长大湖型矿砂船二阶和频非线性激励的贡献能接近线性波激振动的50%[7]。Gu等[8]也对船舶非线性弯矩的高阶调谐成分进行了试验和理论研究。He等[9]研究了顶浪和斜浪下入射波和频波激振动的二阶贡献，在一个典型海况计算中发现，某些站号上非线性波激振动的增大使得总波激振动达到了线性波激振动的5倍以上。顾学康等[10]对一超大型油船进行了线性与非线性波激振动试验，非线性波浪载荷中的某阶倍频成分很容易使船体梁产生共振。小水线面船具有与常规单体排水型船不同的特殊结构形式，其总振动模态较为密集，且形式多样。因此，其总振动受遭遇波浪影响较为严重，不同的遭遇波浪频率、航向、航速以及波高均会较容易激起船体结构的高频振动，而针对SWATH船的波激振动研究较少。

为探究有限幅波中高阶波浪成分对小水线面双体船的振动特性影响，本文从引起波激振动激励源入手，对波浪的频率特性进行分析，在结合高阶有限幅波理论的基础上，推导了受航速、航向、波高、波频等因素影响下的波浪激励力表达式，同时指出了评估波浪参数的决定方法。利用虚拟质量法完成了双体船流固耦合振动响应计算，对比了该船在不同波频参与激励下，船体振动响应的差异。

1 波激振动响应计算理论

1.1 引起波激振动的激励

理论研究和试验研究均认为，非线性波激振动是由非线性波激力产生，且只能产生于船与波浪间的相互作用。马广宗[11]指出，由于船体横剖面或水线面在首部沿深度方向和长度方向的变化是非线性的，从而产生了非线性激励力，并给出了单体船迎浪时的一、二阶波激力表达式

(1)

式中：Ls为船长;Lw为遭遇波长;B为船宽;Hw为波高;d为吃水;C0为考虑浮力和流体动力阻力的修正系数;G2和G3为Lw/Ls的函数，ve为船与波浪的遭遇频率。

常规单体船进行波激振动试验中发现，零航速下波浪遭遇频率变化的低频波浪弯矩能量占主要成分，其它为一些倍频成份；有航速时，按船体梁一阶振动频率变化的高频波浪弯矩占主要成份，比波浪遭遇频率的能量大得多，即存在高阶振动现象。且在有船体梁一阶总振动频率与波浪遭遇频率之间存在倍数关系n。 若n是整数且较小，其峰值明显，则非线性波浪载荷中的某阶倍频成份很容易使船梁产生共振。因此，有必要对波激振动力中遭遇频率的1倍频、2倍频、3倍频等高阶分量进行研究。

微幅波和有限幅波是描述波浪运动常用理论，其波面随位置、时间呈现周期性的起伏，且不变其形状地以固定波速向前传播，在外形上是近似的，如图1所示，它们都属于规则波。常用的微幅波理论是有限幅波理论的一阶近似，有限幅波理论中含有高阶分量，可以独立于船型、有效地解释船舶在波浪中产生高阶振动的激励力来源。微幅波理论要依赖于船体外表面的非线性外型才能勉强解释波激振动的激励力的成因。由于SWATH支柱体的几何外型在垂向是直壁，故在小水线面船上，基于微幅波理论的高阶激励力成因不再存在。

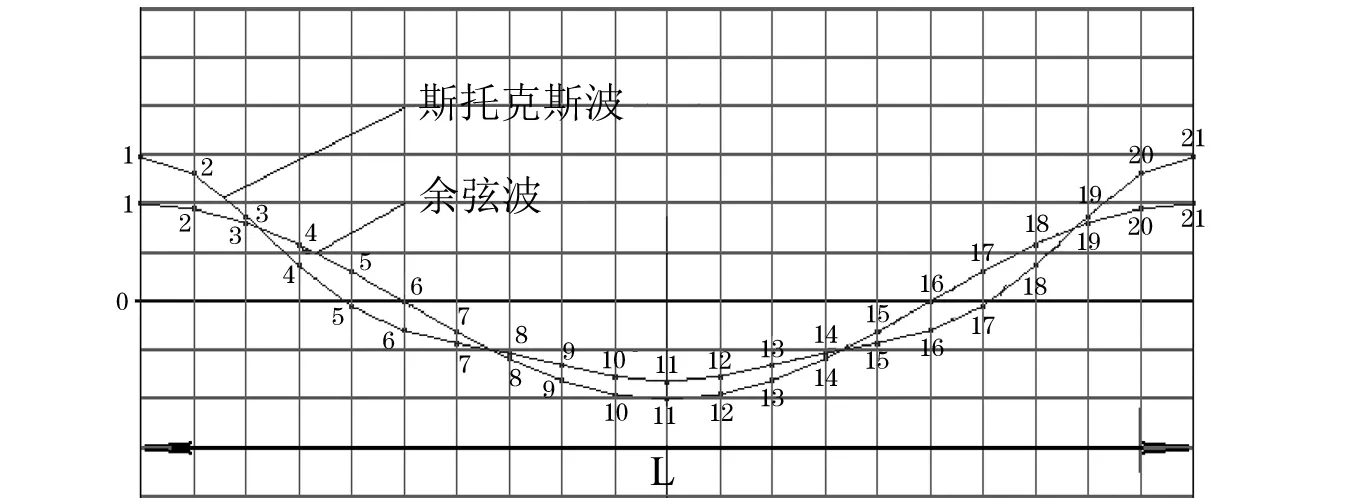
图1 有限幅波与微幅波示意图Fig.1 Finite-amplitude wave and micro-wave diagram

1.2 有限幅波理论下波激振动激励力

静水面在风的作用下失去平衡，受重力和惯性力影响，海面在静水面往复运动，形成波动。设波的传播方向为x,y坐标铅垂向上，波动发生的水域R由下式确定

(2)

式中：d(z,y)表示平面点(x,y)处的深度， 而x0(y)表示由d(x,y)=0解出的显函数。 按势流理论求解变化水域势函数φ(x,y,z,t)的思想，基本方程为

(3)

且式(2)满足-d(x,y)≤z≤ζ(x,y,t)。 如取流场复势为如下形式[12]

w(x+iz)=φ(x,z)+iψ(x,z)

(4)

存在如下边界条件形式：

(1) 自由表面运动学条件

ψ(x,z)z=ζ(x)=const

(5)

(2)表面动力学条件

(6)

式(5)、式(6)中的ζ(x)为波面形状。

(3)有界性条件

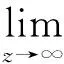
(7)

由式(4)复势求出的自由表面具有周期性起伏， 起伏的周期(即波长)为L=2π/k， 起伏的高度(即波高)为H。 取复势w(x+iz)的试探解为

w(x+iz)=-c(x+iz)+iβce-ik(x+iz)

(8)

令式(5)中的常数为零，则有

ζ(x)=βekζ(x)coskx

(9)

结合以上公式，可得

e2kζ(x)≈1+2kζ(x)

(10)

(11)

将坐标原点置于静水面，并以前进波的形式表示波面，可得波面函数的3阶表达式为(由于太过复杂，本文仅列出3阶)

(12)

式中：c为波的传播速度;H为波高;a为波幅;k为波数。式(12)为深水3阶斯托克斯波，是一种有限幅波。

设SWATH表面在有限幅波中航行时所受到的脉动压力为p(x,y,t)， 根据伯努利方程

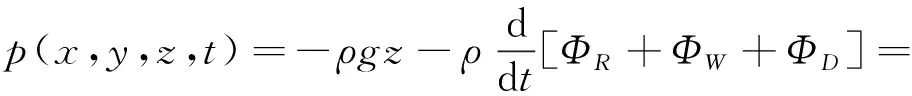
(13)

式中：ΦR为辐射波势，ΦW为入射波势，ΦD为绕射波势。pS为船体运动引起的流体静水压力变化，pR为船体运动引起的辐射压力，pW为入射波引起的波浪压力，pD为船体对入射波的限制而引起的绕射压力。

考虑船的航速，前进波的入射波势函数形式为

ΦW=-c[(x-ct+Ut)+iz]+iβce-ik(x-ct+Ut+iz)

(14)

建立随船坐标系如图2所示，以固定坐标系描述波浪，设船的航行方向与波浪传播方向有夹角μ，则在随船坐标系中，入射波引起的波动压力为

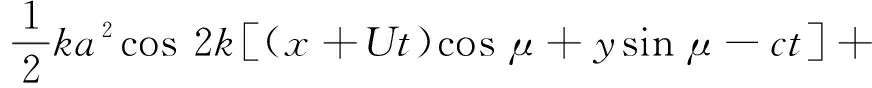
(15)

辐射力{FR(t)}与船舶湿表面的运动有关，可由船舶湿表面速度与水动力系数表示为

(16)

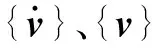
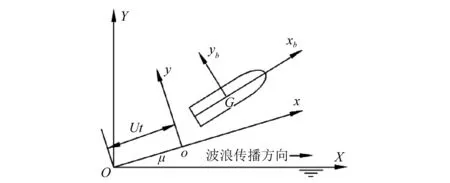
图2 船体运动坐标系Fig.2 Hull movement coordinate system

根据“相对运动”假设，取适当的波浪代表点(如湿表面上点)，设该点各自由度的速度向量为{v}， 则其绕射力{FD(t)}可近似由“等效”的辐射力表示，即

(17)

因此可知，辐射力和绕射力均为流体的附加质量效应和附加阻尼效应。

1.3 评估波浪参数决定方法

式(15)即为激起波激振动的激励力， 其中有1阶力pw1、2阶力pw2、3阶力pw3分量。各阶力的脉动频率呈倍数关系。决定该激励力量值和频率特性的是3个参数：波幅参数a、波长参数k、波频参数c。即存在如下比例关系：

按实际海浪观测资料决定波激振动激励力的基频和激励波的波高、波长参数。

1986年Hogben等提供的目测资料GWS，是经过长期的观测统计给出的全球海浪统计资料，它为海洋结构，特别是船舶结构的设计和作业提供了重要的原始资料。1998年挪威Lφseth提出了对GWS的北大西洋8、9、15及16四海区经修正后的海浪长期统计资料NA-1C。可按该海浪统计资料决定波激振动激励力的基频和激励波的波高参数。

该海浪资料的有义波高为三参数的Weibull分布、跨零波浪周期为log-normal分布。其有义波高的Weibull分布为

(18)

式中：H1=3.041，j=1.484，H0=0.66。 跨零波浪周期的log-normal分布为

(19)

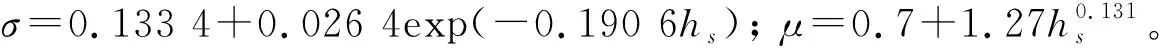
2 整船有限元波激振动响应模型的建立

2.1 整船有限元模型的建立

双体船具有与常规单体船不同的结构形式，振型多样也更为复杂[13]，总振动频率较为密集。双体船模型相关尺度见表1，依据模型资料构造全船有限元模型，纵向基本按1个肋位间距，横向按纵骨间距，垂向基本按纵向构件间距划分，上建甲板层高间划分为5个单元，单元的长宽比尽可能控制在1∶3内。骨架结构采用梁单元模拟，甲板板、舱壁板、外板等板材采用板单元模拟，加强筋和主要支撑构件用梁单元模拟，大设备及液舱质量按点质量单元模拟，使用MPC法加载设备质量。

表1 计算模型的参数

采用全自由边界条件模拟水声测量船在波浪中的情形，采用“剔除刚体模态”的方法实现全自由边界条件模拟。全船有限元模型如图3所示，共有95 760个节点，212 518个单元。

图3 有限元整船模型Fig.3 Whole ship finite element model

2.2 舷外水效应处理

如“1.2”节所述，舷外水与船体的相互作用体现为入射波力、辐射波力和绕射波力这三种形式，且入射波力是导致波激振动的激励力，辐射波力、绕射波力是一种惯性效应和阻尼效应，即惯性力和阻尼力。

对于辐射波力、绕射波力中的惯性效应部分，则采用MSC.Nastran程序中基于流固耦合理论的有限元技术进行模拟，即虚拟质量法。该方法利用Helmholtz理论，通过在外部边界上分布一组“源”，每个“源”产生一个微分方程的简单解，求解Laplace方程。推导出一个虚流体体积产生一个质量矩阵，该质量矩阵表达流体与一个结构单元组成的边界耦合和其它影响。

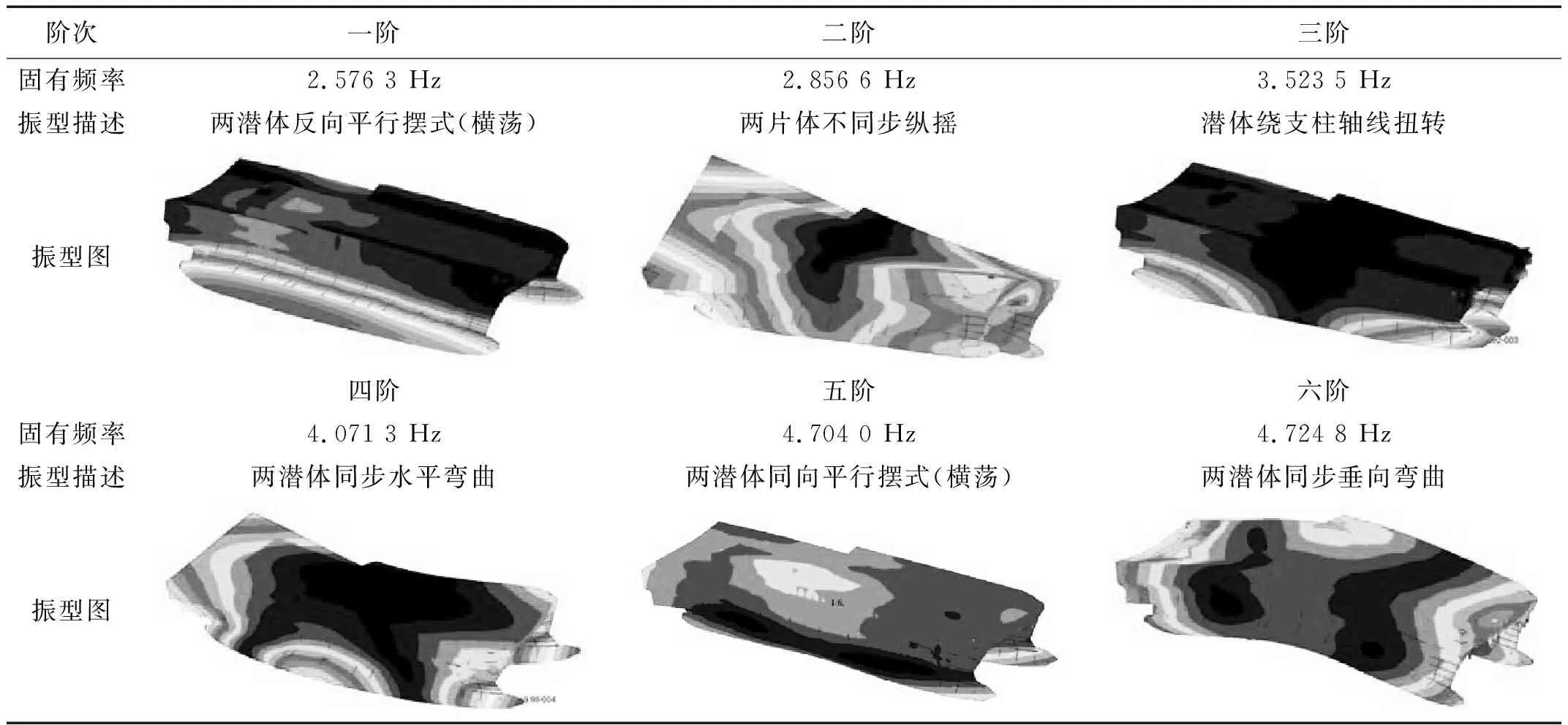
表2 整船总振动频率和振型数值计算结果

虚质量法适合于下列问题类型：

(1) 包围部分结构的无限流体；

(2) 带自由界面、内含可弯曲变形结构的流体；

(3) 由上述情形组合的多个流体体积。例如：漂浮在水中的一半，带有几个内部容器，内部容器具有自由界面和对称边界。

表2给出了考虑流固耦合效应的总振动固有频率及其对应振型。

由海浪理论和实测海浪谱可知，主要规则波波频多在0.1 Hz附近，且一般不会超过1 Hz。据表2中固有频率可见，该船总振动的低阶固有频率值均远大于波浪频率，不会发生线性波激振动。但波浪的倍频成分及其激励力幅值、结构刚度、结构阻尼均会影响结构的振动响应的剧烈程度，由波浪高阶分量产生的结构振动问题不可忽视。

秦铁崖伸手示意：“这是刑部赵大人交给我的差事，现在交差。我已给老仙翁说好，腾一座小院出来，专供你表姐居住。”说罢拱手告辞。

2.3 波浪载荷的施加

受波浪作用的船体，在载荷作用的每个变化周期内，波浪在船体水线附近的作用位置(湿表面)是变化的，即力的作用点是“场变的”，此外，这部分船体湿表面所受的波浪力是随时间变化的、是非连续的，即力的大小和方向是“时变的”[14]。本文采用移动波浪激励力直接加载技术进行波激振动响应计算[15]，将式(15)所描述的波动压力以面压力的方式直接作用在整船有限元模型的湿表面上。

设在固定坐标系O-X1Y1Z1中， 记某瞬时的波型方程为ξ(x1,y1)， 波轴在静水面上。 对所选取的波浪在OX1Y1面内进行旋转变换可得在随船坐标系O-XYZ中的波型方程ξ′(x,y)。 设小水线面船在静水中的吃水用随船坐标系表示为ξ0(x)， 则

ξJ(x,y)=ξ0(x)+ξ′(x,y)

(20)

以板壳单元离散小水线面船的船体表面， 设第i个节点的坐标为(xi,yi,zi)， 则有第i个节点吃水为

di=ξJ(xi,yi)-zi

(21)

在随船坐标系中，记波浪压力载荷为q(x,y,z)， 对于第e个单元，其平均压力为

(22)

式中：Se为第e个单元的面积。

当单元划分得足够小时

(23)

将波浪载荷函数转换成用PCL语言描述的Field函数作用于船体上，即实现了波浪对小水线面船整船有限元模型的加载。

3 波激振动响应计算结果

3.1 计算工况

按实际海浪观测资料决定波浪激励力的基频和波高参数，重点对5级、6级、7级海况进行分析，定义波高为3.25 m、5 m、7.5 m，对应于各级海况波高的上下限均值。船体强迫振动位于共振区时需考虑阻尼，将其与内阻尼合并考虑，按照规范中关于水面舰艇模态阻尼系数的规定[16]，见图4(取低阻尼)。

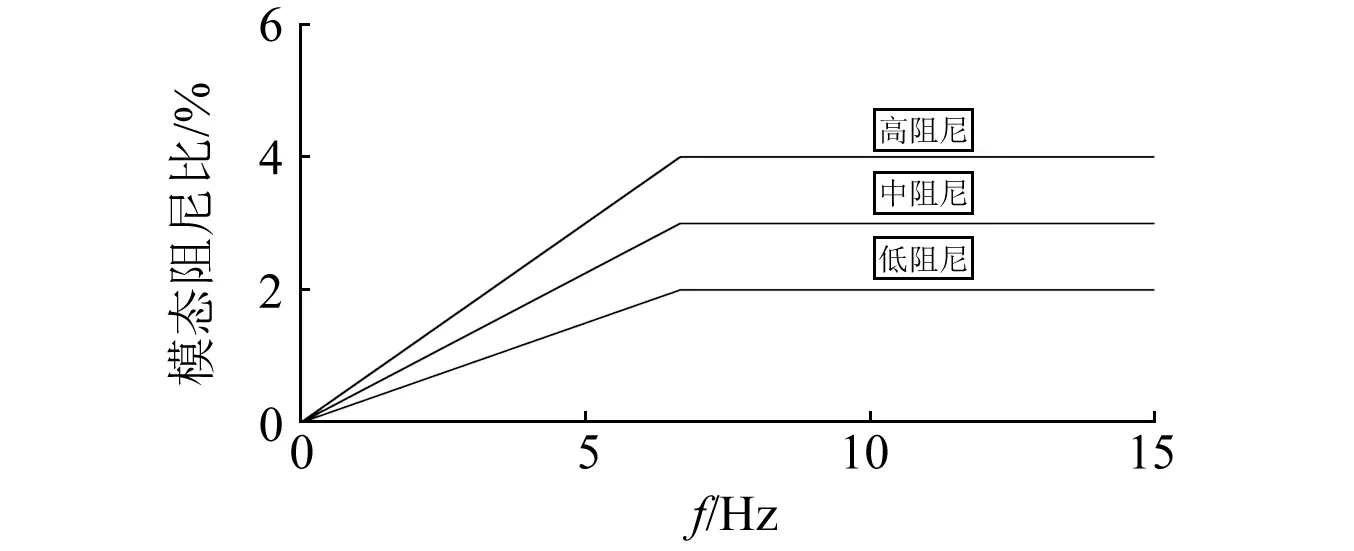
图4 水面舰艇模态阻尼系数Fig.4 The modal damping coefficients of surface ship

根据NA-1C海浪长期统计资料的波浪参数概率分布规律， 计算波浪取最大概率波浪，即在本级海况有义波高条件下，波浪周期有最大发生概率p(tz/hs)的规则波，p(tz/hs)按式(19)进行计算。

表3中列出了5级、6级海情下波浪参数和概率。表4中给出了15个计算工况，其中包括5级海情下0 kN、6 kN和12 kN航速， 180°、135°和90°浪向角的9个组合工况，6、7级海情下12 kN航速， 180°、135°和90°浪向角的6个组合工况。对于各个组合工况分别对比计算由三阶有限幅波、二阶有限幅波和一阶有限幅波(微幅波)激励下的船体波激振动响应。

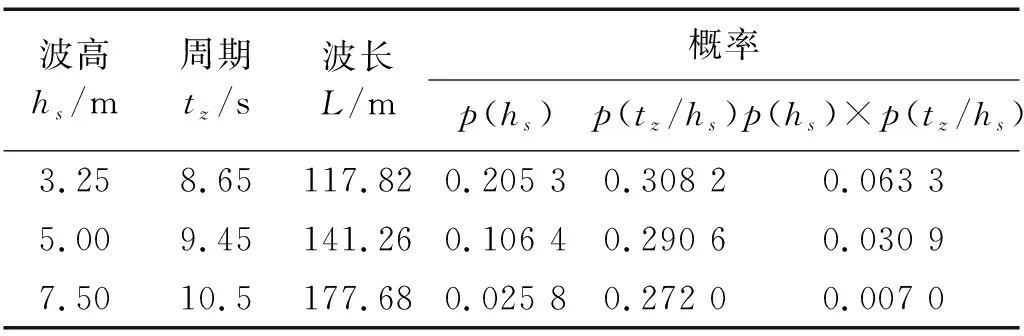
表3 波浪参数及发生概率计算表

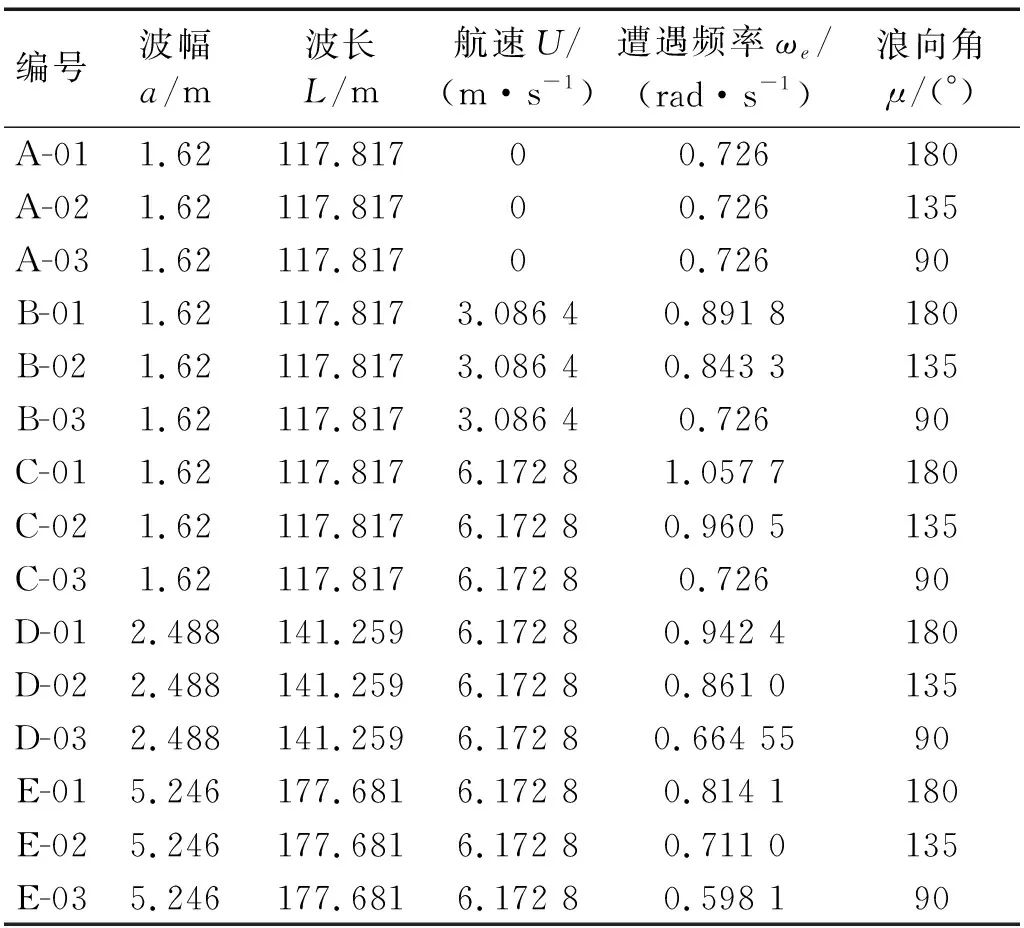
表4 数值仿真试验计算工况

3.2 非线性波激振动响应对比结果

采用瞬态响应分析对船体动响应进行预报，参考《水面舰艇振动评价基准》中关于评价区域的要求，对1甲板艏、艉端的左、右舷边以及船舯的左、右舷边的6个位置处的加速度响应进行计算，取总时长40 s内的时域响应信号进行处理。以顶浪工况组为例，图5给出了A-01、B-01、C-01和D-01三种有限幅波激励作用下1甲板艉端左舷边的时域加速度响应。

图5 顶浪航行状态下1甲板左舷端时域响应Fig.5 Time-domain response of 1st deck stern side port side in the state of surfing sailing

为直观对比波浪的高频成分对船舶振动响应的影响，计算得到平均振动加速度级

(24)

式中：n为测点总数;Li为第i个测点的振动加速度级曲线，dB； 振动加速度基准值：a0=10-6m/s2。振动加速度总级为：

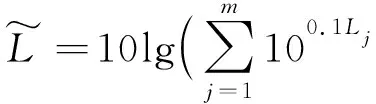
(25)

式中：Li为测点第j个频率点的振动加速度级， dB；m为频率点总数。

将时域响应数据进行频域转换，得到船体1甲板上6个响应测点在0～10 Hz内三阶有限幅波、二阶有限幅波和一阶有限幅波(微幅波)激励下的船体波激响应平均振级，测点的频带平均总振级见表5。

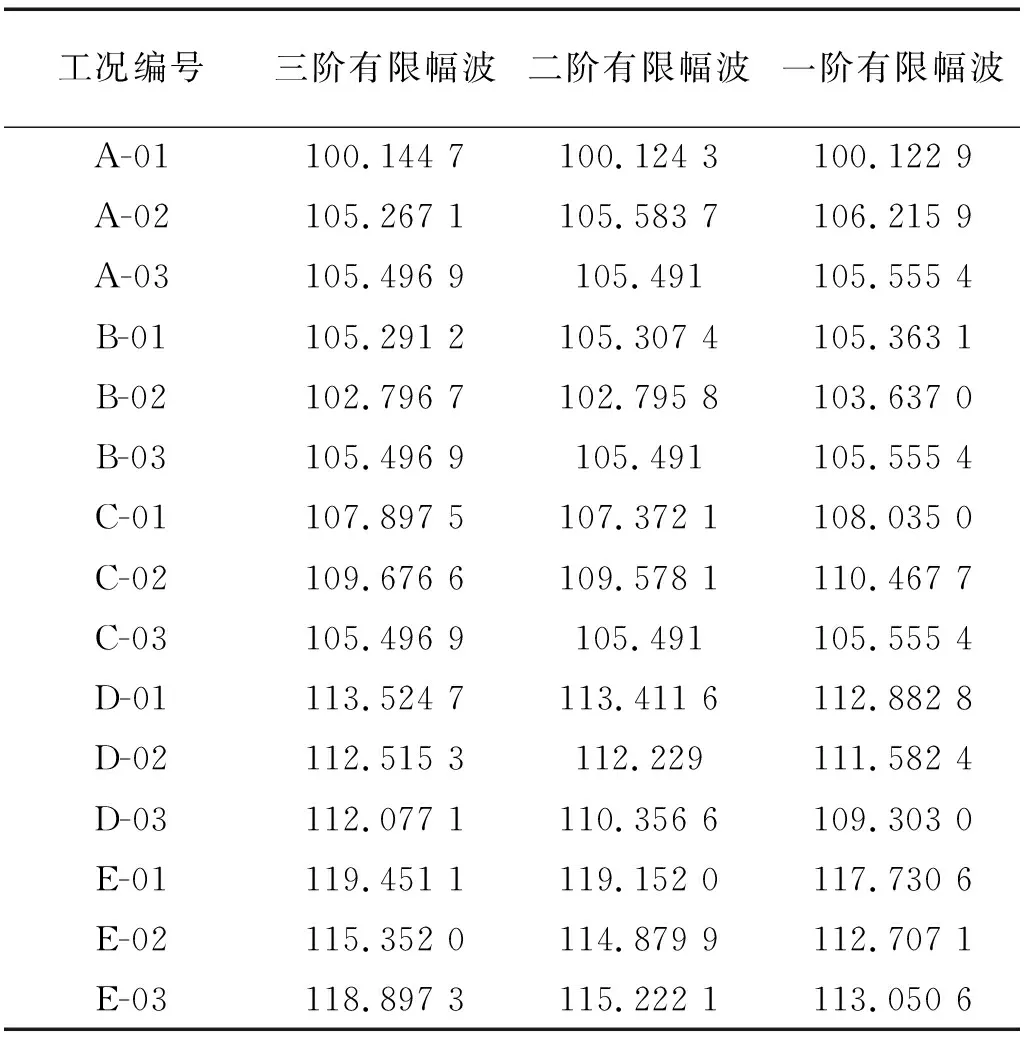
表5 1甲板6测点平均加速度响应总振级

可见，零航速下(如A-01～A-03工况)，受斜浪和横浪载荷作用时，船舶振动更为剧烈，总振级较其它两个工况高出约5 dB；有航速状态下，船舶高航速时振动更为剧烈(如A～C工况比较)；斜浪航行下，船舶振动普遍较为剧烈，且与海况成正比关系。

根据表5中按不同阶次的有限幅波载荷作用下的振动响应计算结果，波浪中的高阶成分对船舶激励具有不可忽略的影响，随着海情的升高，这种非线性效应表现的更为显著。例如在D-03、E-03工况中(见图6)，按微幅波理论与按三阶有限幅波理论的总振级计算结果分别相差2.77 dB、5.85 dB。在某些特殊的低海情下，三阶有限幅波、二阶有限幅波、一阶有限幅波加速度响应振级基本相当，有限幅波的高阶成分未能显著激起船舶的非线性振动，所得计算结果与微幅波理论较为接近。因此，在研究高海况下的船舶波激振动时，非线性波激振动问题应予以重视。

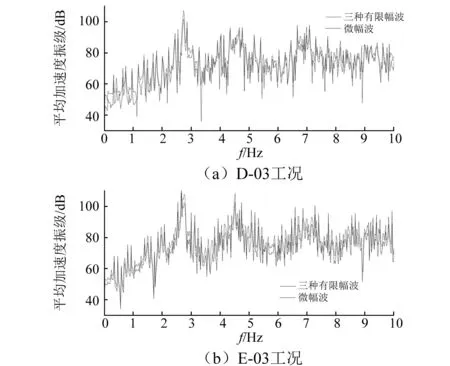
图6 加速度响应振级对比Fig.6 Comparison of acceleration response vibration level

4 结 论

本文从引起波激振动激励的源头出发，通过有限幅波理论，在独立于船型情况下有效地解释了船舶在波浪中产生高阶振动的激励力来源。对比计算了某双体船在不同波频参与激励下，船体振动响应的差异。可见，在大多数海情下(特别是高海情)，即使船舶总振动固有频率与波浪频率相差较大，有限幅波中高阶成分亦可对船舶产生高频激励，因此，利用有限幅波理论分析船舶高频振动更具有指导意义。