一种基于RSSI指纹和DOA信息的单基站定位方法
吕小微
(中国电子科技集团公司信息科学研究院)
0 引言
当前,无人机集群因其执行任务效率高、适应能力强、成本低廉等优点,已发展成为无人机领域的热点研究问题。无人机集群技术是无人系统效能的倍增器,也是无人系统未来的发展趋势。以美国为代表的研究机构部署了多个项目专门研究该项技术,在系统架构、软件算法、微小型化、低成本低功耗实现等方面全方位的提升无人机集群的自主控制能力[1][2]。尽管卫星导航系统因其高精度、全天候、全时段的特点,在国计民生的方方面面都得到了广泛而深入的应用,但其固有的缺陷也限制了其在某些复杂环境中的可靠应用,如建筑密集的市区、深山峡谷、室内地下等物理阻碍环境下、或存在电磁干扰、屏避的敌对环境中,基于卫星的导航将不再可靠[3]。另外,从使用成本的角度来说,大量密集部署的无人机集群,倘若均安装卫星导航系统,无疑将对使用成本造成巨大挑战,尤其是在微小型的飞行载体上,将会造成平台资源的巨大浪费。因此,无人集群多目标间协作将是支撑集群技术发挥优势的关键技术之一。
目前,针对无人集群的协作式或网络式导航与定位研究较为综合而全面[4][5],如基于多传感器信息融合的相对导航技术[6][7]、基于几何特征的协同导航[8]、基于生物启发的协同航迹规划[9]、以及面向微小型无人集群的协作式导航[10]等。同时,也出现了一些针对单基站的导航方法,如仅采用测距的方法来分析飞行位姿的方法[11]、采用基于UWB信号的TOA/AOA的混合定位方法[12]等。本文从协作式导航与定位的角度入手,提出一种仅利用单个目标锚节点即可实现对其它移动目标节点的定位机制,可为较为严酷环境下的无人设备自主导航与定位应用提供多样化的问题解决手段。
1 问题描述
无人集群常见的编队模式为主从式编队,编队队形有楔形、梯队、横/纵队和 V形队等,集群数目少则两三架,多则数百千计。本文假设,采用V形编队的主从式集群中的一架从机不具有或丧失导航能力,仅通过集群中的另一架在有效通信距离内、且具备自主定位能力的长无人机进行定位。设具备自主定位能力的目标为节点A,其以速度VA沿直线作匀速运动,为锚节点;无导航能力的无人机为节点B,以速度VB沿与目标A成角度α的直线作匀速运动,为目标节点。二者保持在同一水平面,即在二维平面上运动。在t∈{1,2,…,T}时间段内,目标A和目标B的位置坐标分别记为和其中,T为目标B丧失联络的总时长。在每一时刻t,目标A和目标B将分别从两个维度测量二者之间的测量信息,即信号到达方位(DOA)信息和接收信号强度(RSSI)信息。其中,方位角度信息记为θt,t∈{1,2,…,T},接收信号强度信息表述为rt,t∈{1,2,…,T}。在时刻t,二者的相对位置和测量信息关系如图1所示,失联目标节点B,由黑色圆圈标记,锚节点A,由黑色三角标记,二者间测量相对角度记为θt,θt∈{0,….90°}。节点B所测来自锚节点A的接收信号强度为rt,且该信号强度理论上呈以点A为中心、半径为满足接收信号强度为rt的距离的弧形区域内均匀分布,分布象限为第一象限。
2 定位算法分析
本文方法是一种基于方位和接收信号强度指纹信息(fingerprints)的融合定位方法。基于指纹信息(fingerprints)的定位是一种基于场景特征的位置估计方法[13],将信号在传播过程中可能遇到噪声、障碍、多路径等因素影响考虑在内,利用预先的信号特征测量来构建场景中的信号特征指纹库,并通过信号模式匹配来识别目标实时的位置信息,具备一定的抗干扰能力。
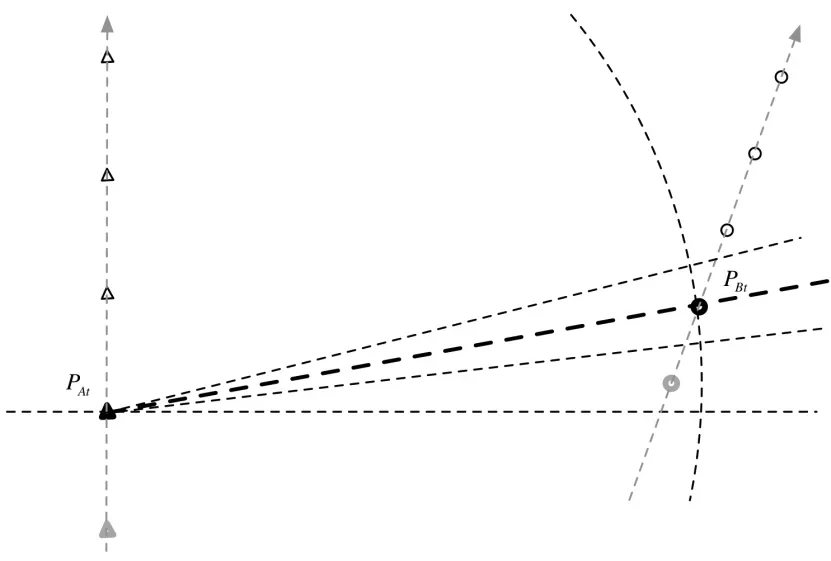
图1 t时刻两目标相对方位和信号测量示意图
在本文中,运动目标节点B通过基于指纹信息的定位方法获取所有可能满足条件的估算点,且这些估算点相对距离呈弧线状分布;同时,通过测量与锚节点A的角度信息获取节点B的方位信息,将该方位信息引入不确定度数值θδ形成扇形区间;前者所获取的弧状带将与扇形区间产生交集,根据该交集采用K近邻域的方法对运动目标B的位置进行估算。
2.1 基于指纹信息的相对位置估算
节点B的第一个位置估算利用两节点间的接收信号强度(RSSI)值通过指纹信息匹配的方法进行计算,为此需预先对场景中的信号分布进行采集和建模。
假设有一个移动锚节点,在预设的锚节点A的运动轨迹上移动,在每一个位置向网络中发射信号。由于信号强度随信号传播距离的增加而减少,那么网络中的任一节点将唯一对应一组来自不同位置锚节点发射信号的接收信号强度[14]。这些锚节点的位置可记为网络参考测量节点的位置可记为在测量过程中,通过把一个目标节点依次放置在这些参考位置上,测量发自锚节点A的信号的接收信号强度。这些数据可记为j∈{1,…,n}。这些数据将存储在数据库中,以便与实时的测量数据进行比对,并对实时运动节点位置进行估算。
在实际运动场景中,运动节点B在每一时刻t测量其与运动中的锚节点A之间的接收信号强度rt。在t∈{1,2,…,T}时段内,这些实时接收信号强度记为在时刻t,每一个实时测量信号强度rt在与数据库对比时,选用同一锚节点位置的一组参考信号强度信息j∈{1,…,n},即将从所有n个参考节点中选取M个最接近于rt值的,m∈{1,…,M}。由于每一个实时测量信号强度rt将仅接收一个锚节点信息,不难看出所有满足要求的pCk分布在距离锚节点A所在位置pAt等距的圆弧带上,如图 2中弧线附近圈状圆点所示。
2.2 基于角度信息的相对方位估算
通常,如采用基于角度的定位方法AOA[15][16],需要两个锚节点发射方位信号,通过测量两个锚节点与目标节点之间到达信号的相对角度并利用几何计算原理估算出目标节点的位置。本文考虑相对严格的背景环境,即在时刻t有且仅有一个锚节点可利用时,通过节点自身携带的阵列天线可测得目标节点B与锚节点A之间的相对方位角度,且目标节点B将分布在信号在该传播方向上的延长线上。
由于信号在传输与测量的过程中不可避免地存在一定的误差,为后续解决单基站定位的问题,引入测量角度不确定度的概念,记为δθ。那么,时刻t实际测量的目标节点B与锚节点A之间的相对角度θt将重新表述为区间数值的形式,并记为t∈{1,2,…,T}。由此,如图3所示,目标节点B将重新定位在信号在该区间传播方向上的扇形延长区域内。

图2 基于接收信号强度指纹信息的定位示意图
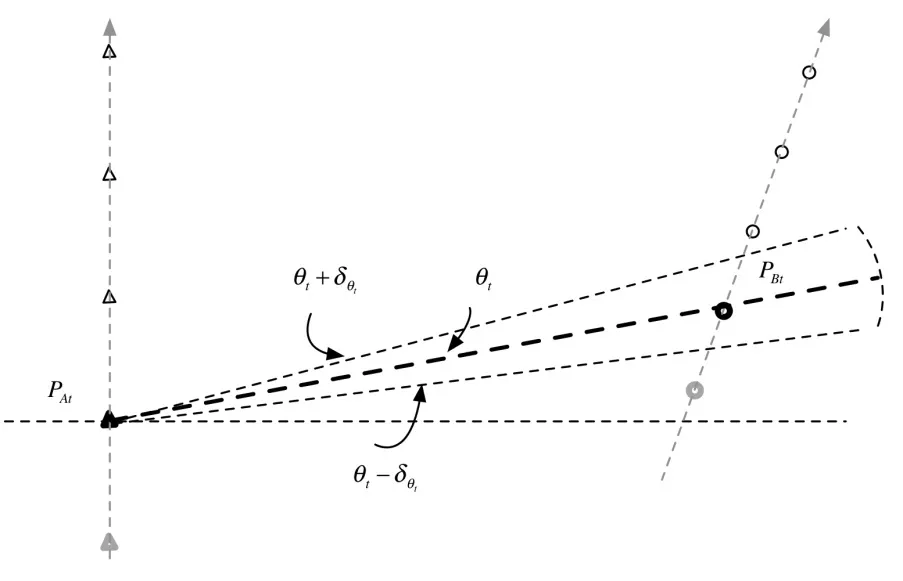
图3 基于方位角度信息的定向示意图
2.3 基于单一锚节点的运动节点位置估算
显然,当仅利用一个锚节点时,单一的采用角度或指纹的方法并不能实现对运动目标的准确定位。仅利用指纹方法,将仅能获取距离锚节点A位置pAt等距的圆弧带区域,二者间的相对方位仍无法确定;仅利用测量到达角度的方法,将仅能测得目标节点B与锚节点A之间的相对方位角度,二者之间的相对距离仍无法确定。
为解决这个问题,本文将两种定位机制进行融合处理,并在测角的方法中引入了角度不确定度θδ。假设θt′为时刻t目标节点B与锚节点A之间的真实方位角度,那么测量值与真实值之间的关系可记为其中,测量噪声εt呈均值为零方差为σθ的高斯分布。如果所选取不确定度值即可以99.7%概率确定真实的′包含在内,即目标节点B将可信地定位在[θt]区间传播方向上的扇形延长区域内,如图4中以为弧心以为角度的扇形虚线内区域所示。

图4 基于角度与信号强度指纹信息的融合定位示意图
基于接收信号强度的指纹估算将锁定在呈近似弧状分布的以距离锚节点A位置pAt为弧心、所有满足等距接收信号强度tr的参考节点pCm上,如图4中圈点参考节点所示。结合基于角度测量的方位估算,首先选取所有满足分布在扇形区域内的参考节点,继而根据K近邻域算法[17]选取交集区域内满足K个最近的欧氏距离的选取的节点如图4中的较大圈节点所示。每个选取的pCk将依据所计算的距离分配权值,时刻t目标节点B的位置将由基于权值的位置估算确定,如图4中星号所示。
3 仿真结果
假设两架无人机在100m×100m的二维空间作相对运动,沿北方向以速度VA=3m/s匀速运动的无人机具有定位能力,标记为锚节点A,沿北偏东向以速度VB=2.9m/s作匀速运动的无人机标记为待定位节点B,节点B的初始位置在一定的区间随机选择。依据上述定位原理,在任一时刻t,节点B的定位都是独立的。为便于仿真,假设测量时间间距为1s,测量飞行时间T=25s。
为执行第一种基于接收信号强度指纹的估计,首先在节点A和B的飞行区域设置若干锚节点与参考节点位置,锚节点为T个,固定均匀分布的参考节点设为 2450个。仿真的接收信号强度值均依据Okumura-Hata模型[18]由锚节点与参考节点之间的相对距离计算获得。所有 RSSI信号加入标准方差rσ=0.2dB的高斯白噪声,约为所有数据标准方差值的5%。同时,目标节点B与锚节点A之间的相对角度tθ由二者之间的位置坐标计算,并加入标准方差θσ=0.02rad的高斯白噪声,角度测量不确定度值选取为θδ=0.05rad。
仿真中,如图5(a)所示,锚节点A沿固定线路运动,由黑色三角标识;节点B的初始位置在一定的区间随机选择并沿与A成固定角度的线路同步运行,由黑色圆圈标识,时刻t真实位置由黑色空心星号标识。在时刻t,同步测量二者间的接收信号强度与相对方位角度。基于接收信号强度指纹的带状位置估计结果如黑色圈点所示,基于角度测量的方位估计如黑色虚线夹角区间内区域所示。在二者交集区域内根据K近领域算法选取的参考节点标记为最大半径的黑色圆圈,节点B估计位置标记为黑色星号。节点B运动路线的最终估计如图5(b)所示的黑色星号连线所示。统计估算误差由目标节点飞行T=25s时间段内的实际位置与估计位置误差的平均值决定,且仿真结果采取执行100次的平均值。表1所示结果分别统计了在参考信号节点不同密度条件下和不同噪声标准方差值条件下的定位精度,估计精度随节点密度的增加和噪声方差值的减小而提升。仿真结果表示,当目标运动在约为80m×80m的定位范围内,本文方法仅利用单个基站的测量即可达到1~2m的定位精度,体现了较为优良的定位性能。
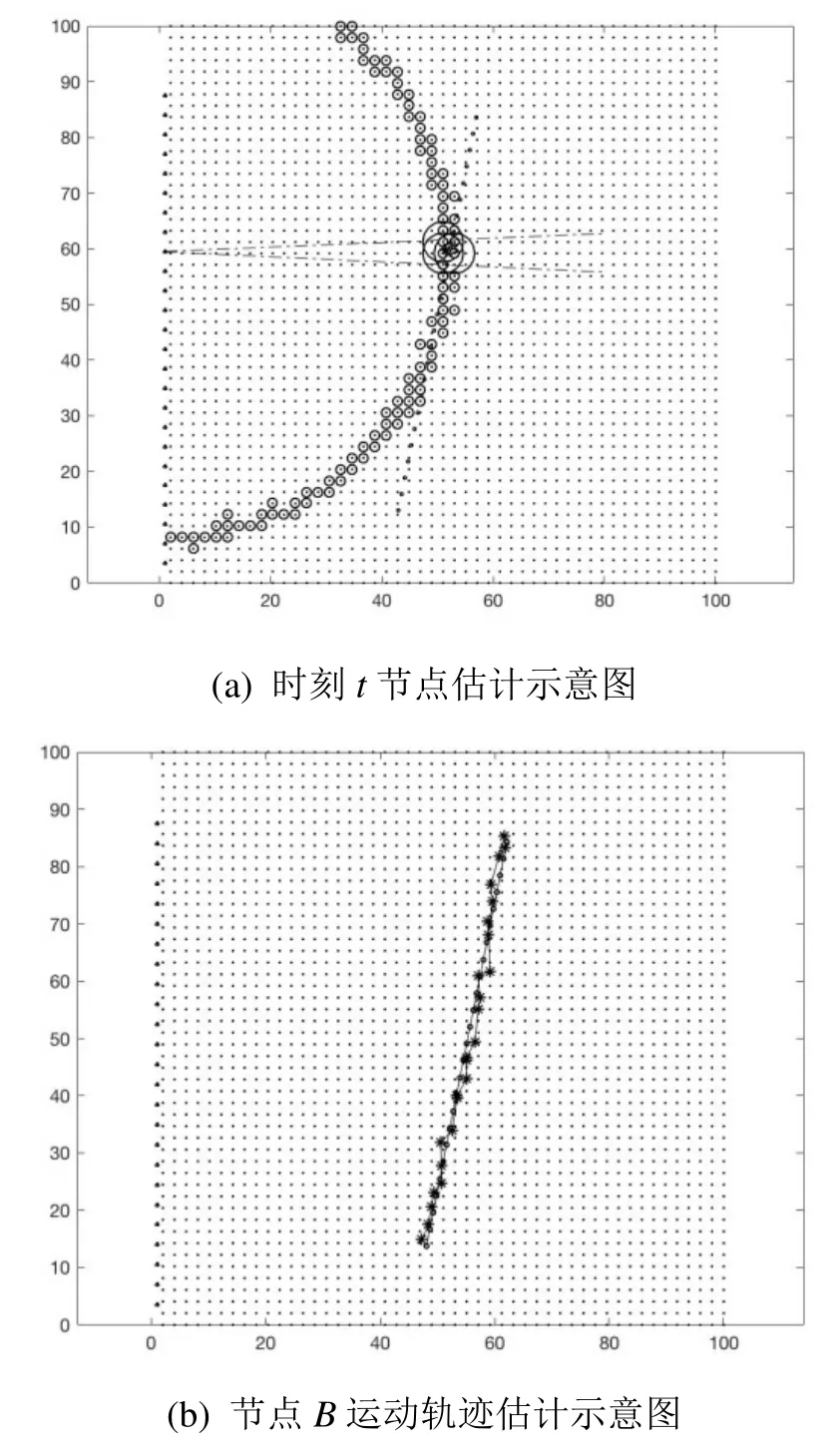
图5 基于角度和指纹融合处理的单基站定位示意图

表1 基于角度和指纹融合处理的定位估算误差
4 结论
本文提出了一种新的基于单基站的移动节点定位机制和方法,它利用锚节点与目标节点间的相对角度信息来确定目标方位,利用基于接收信号强度的指纹信息来确定相对距离半径,并引入信号不确定度的概念来标定采样区间;其在每一时刻的定位也相对独立,即便在某一时刻丢失也不会影响下一节点的定位操作,在一定程度上解决了集群系统因导航资源受限而无法准确定位的局限问题,提高了集群协同导航与定位的适应性与可靠性。当然,值得注意的是,本文的定位方法考虑的背景环境较为理想,在强噪声干扰以及非视距(NLOS)环境下的定位适应性问题仍有较大的探讨空间[19][20]。

