K波段低副瓣波导缝隙驻波阵设计
杨彦炯
(中国电子科技集团公司第二十研究所,西安 710068)
0 引言
波导缝隙阵列天线广泛地应用于雷达系统中[1],其口径电场幅度和相位分布能精确控制,且具有结构紧凑、辐射效率高、功率容量大、可靠性高、损耗小,易实现高功率、高增益、低副瓣、窄波束和赋形波束等设计要求;其次,波导缝隙馈电网络与辐射口面一体化设计的平面结构剖面低、结构紧凑,方便与各型载体共形。鉴于以上优点,平板波导裂缝阵列天线广泛应用于雷达、通信与导航系统中。目前,在敌我识别和导引头雷达系统中均采用平板波导缝隙阵列天线[2~3]。
1 理论分析
波导缝隙天线的幅相分布可由缝隙偏置或倾角的大小和方向来控制,按照缝隙位置可分为宽边偏置缝隙阵、宽边倾斜缝隙阵、窄边倾斜缝隙阵。依设计极化要求,本文中天线采用宽边偏置缝隙,图1所示为所涉及阵列天线结构示意图及其等效电路[4]。

图1(a) 平板缝隙的示意图

图1(b) 波导缝隙阵列等效电路
采用端馈或者中馈形式且终端短路的波导缝隙天线,其单元间距为λg/2时,此时波导腔体内的电场呈驻波状态,这种形式的缝隙阵称为驻波阵。对于偏置缝隙,假设终端短路板距末端缝隙间距为λg/4时,缝隙总是位于驻波电压波峰点。驻波阵是一种窄带天线阵,在进行辐射阵面设计时,需要根据带宽要求划分适当数目的子阵。本文中天线带宽不足1%,无需做子阵划分。
对于无耗传输线,距离负载为d的参考面输入阻抗为:

式中,Zin(d)为参考面的输入阻抗,Z0为传输线的特性阻抗,Z1为负载阻抗,d为到负载的距离。这样,归一化导纳为:

其中,y1为负载的归一化导纳。
对于长为Ls的短路线,其归一化输入导纳为:
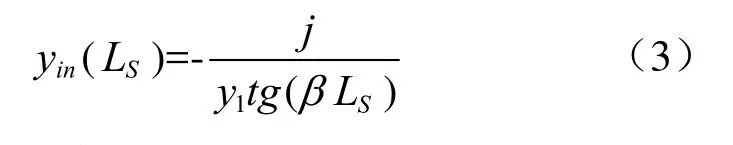
那么图1(b)中的yin1为:

相应的,图1(b)等效电路中yin2为:
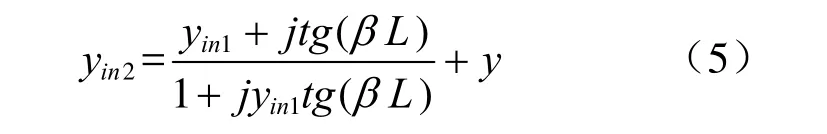
以此类推,可以得到开有N个缝隙的波导上的第N个缝隙处的归一化导纳的递推公式:
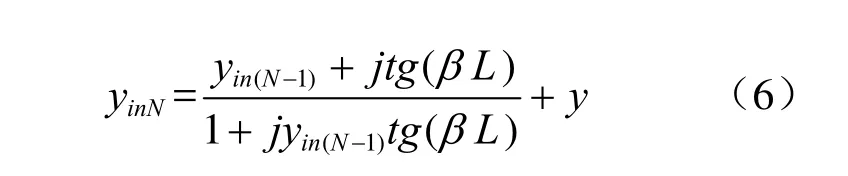
由此,可得波导端口处的归一化导纳为:
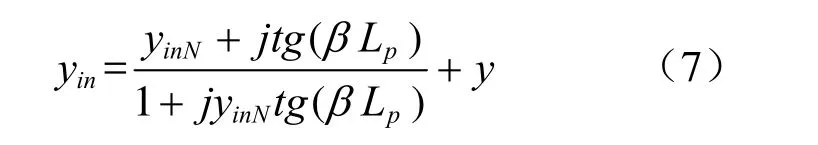
由式(7)可以看出,由传输线理论得到的端口归一化输入导纳为缝隙归一化导纳y的函数。
为求得缝隙的归一化导纳值,利用HFSS仿真得到驻波阵端口的反射系数S11,反射系数和导纳之间有如下关系:
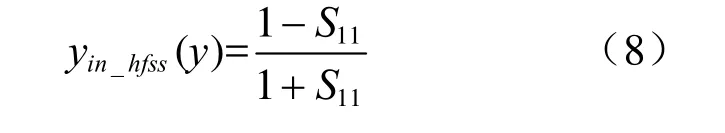
用式(7)和式(8)建立方程可得:
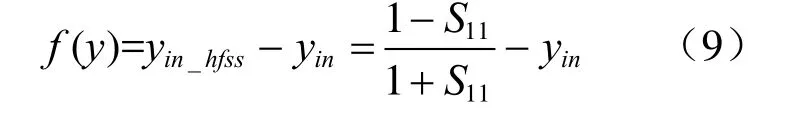
求解方程f(y)=0,即可得到各缝隙归一化导纳值y。
2 导纳参数提取
驻波阵缝隙间距d=λg/2,d初始值取为9mm(中心频率24GHz,选取BJ260标准波导对应波导波长λg=18.11mm),d最终取值可根据仿真结果做微调。使用Ansoft HFSS仿真软件,建立N元(本文取16)缝隙阵仿真模型,缝隙尺寸完全相同,且相邻缝隙交替偏置。
通常宽边偏置缝主要提取缝隙偏置量和缝隙长度两个参数,提取的步骤如下:
(1)固定缝隙偏置量offset1,以缝隙长度long1做参数扫描,S11为因变量,找到S11最小时对应的缝隙长度long1,即可得到缝隙偏置offset1缝隙长度为long1时最小值S11min1。
(2)调整缝隙偏置为offset2,固定其值不变,重复上述步骤(1),即可得到缝隙偏置offset2,缝隙长度long2时S11的最小值S11min2。
根据指标要求副瓣电平≤-27dB,单元的幅度分布按副瓣-30dB泰勒分布计算,单元数即缝隙数目为30个,等副瓣数为5[5],可得到各缝隙理论幅度分布如图2。
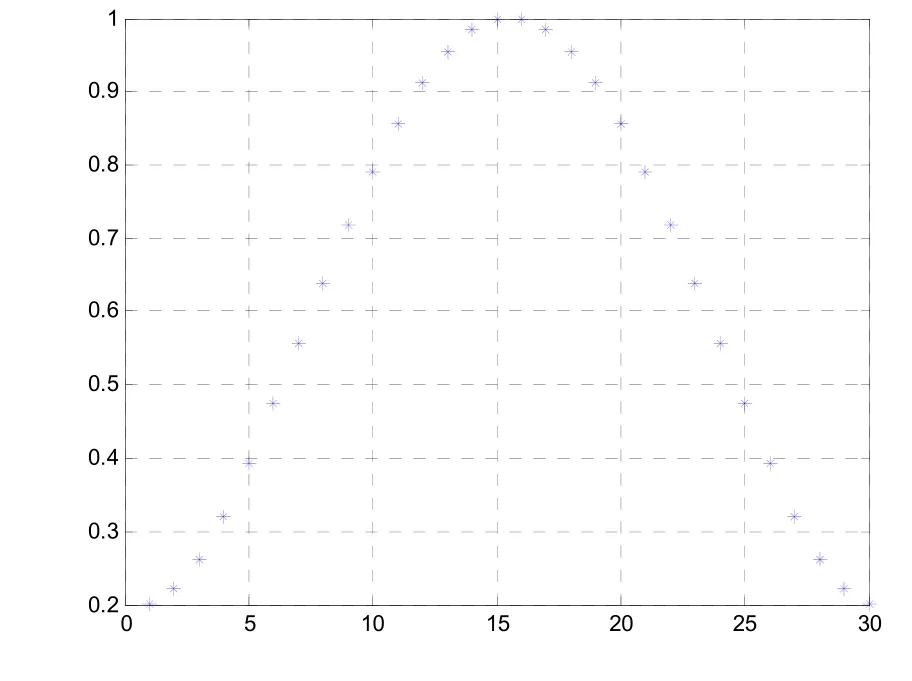
图2 各缝隙理论幅度分布
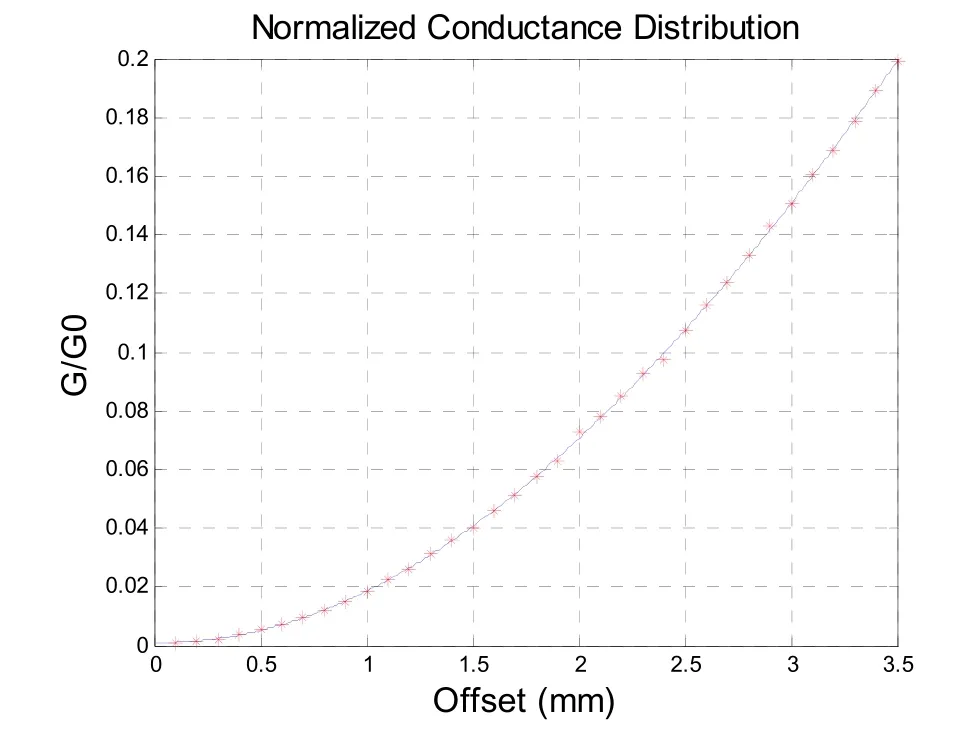
图3 缝隙偏置与电导关系曲线

图4 各缝隙电导分布曲线
上节中公式已经将电导与S11建立关系,本节使用仿真软件建立了缝隙偏置量与S11之间关系,由此可将缝隙偏置量与电导进行曲线拟合,得到拟合曲线如图3所示。根据计算得到的缝隙理论幅度分布值可得各缝隙电导分布曲线如图4所示。
3 仿真结果
确定缝隙各参数后,建立仿真模型,如图5所示,共3层。最上层为辐射缝隙,缝隙总数为30×16,即方位30个缝隙,俯仰16行缝隙;中间层为宽边辐射缝隙传输波导;最下层为平板波导缝隙馈电波导。优化阵面各可调参数,得到满足指标的仿真结果,如图 6~图 8所示分别给出频率 23.95GHz、24GHz、24.05GHz的方位面方向图。

图5 天线仿真模型
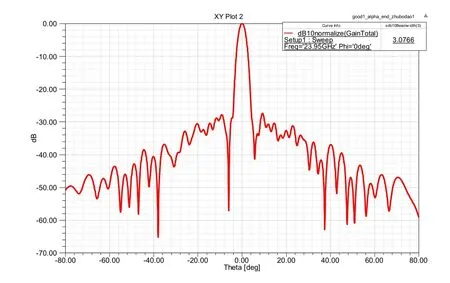
图6 23.95GHz方位面仿真方向图
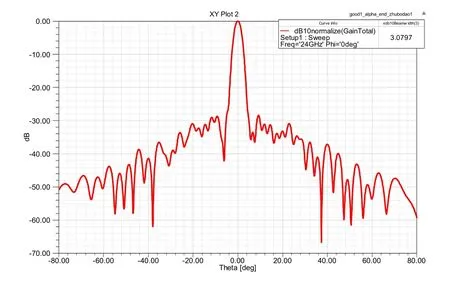
图7 24GHz方位面仿真方向图
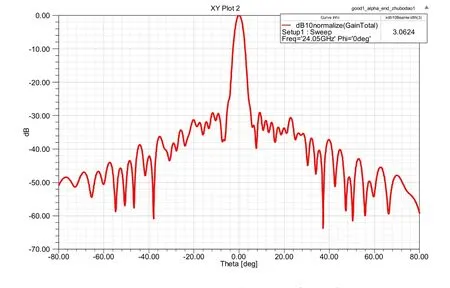
图8 24.05GHz方位面仿真方向图

图9 K波段平板天线实物

图10 23.95GHz方位面实测方向图
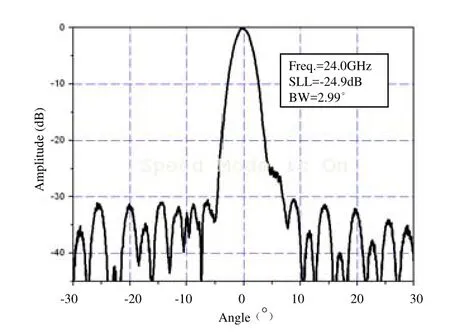
图11 24GHz方位面实测方向图
4 实物测试
按图5模型加工天线阵面(图9),天线最终尺寸为275mm×198mm×15.2mm,图10~图12为方向图测试曲线。表2为天线阵面仿真结果与实测结果比对,可见天线波束宽度仿真与实测结果吻合;天线左副瓣仿真与实测结果吻合,但右副瓣抬高,为加工误差引起;实测增益小于仿真增益为比对法测试误差所致。

图12 24.05GHz方位面实测方向图

表2 天线仿真实测结果比对
5 结论
本文设计了一个K波段低副瓣波导宽边缝隙驻波阵天线,理论计算结合仿真分析,得到设计副瓣电平对应缝隙参数。对整体模型进行优化设计,得到满足指标设计结果。

