基于改进Rosenblueth法的水电站边坡可靠性分析

杨 奎

(浙江省水利水电勘测设计院 惠州分院，广东 惠州 516000)

1 概 述

在我国水电开发的大背景下，许多大型水电站相继投入建设。水电站的建设将给当地流域的环境带来一定的影响，水电站蓄水后，边坡两岸岩体受到水压力及水力侵蚀的作用，岩体变得疏松，影响水电站边坡的整体稳定性，蓄水过程带来的库岸边坡变形破坏等稳定性问题逐渐成为制约水电开发的工程地质问题之一。大型水利工程蓄水后将形成大量的涉水边坡，导致水电站边坡的稳定性易受到区域环境条件的影响，如气候、降水等。水电站边坡的稳定性是自然因素与人为活动共同作用的产物，具有复杂的系统性，存在较多的不确定性因素。

边坡安全系数是岩质边坡稳定性评价应用最广泛的指标。实际工程中，通常采用抗滑力与滑动力的比值来定义安全系数。虽然形式简单，但带有较多的经验成分，并且它是建立在确定性的概念之上。岩质边坡岩体的稳定性受岩的岩性、强度、构造、地下水位的高低、结构面的产状和位置、爆破震动等因素影响，导致稳定性计算中含有若干不确定性。为克服现有稳定性计算的缺点，建立在不确定性概念之上的概率分析法被引入到岩质边坡的稳定性评价中，结合公式计算法与概率分析法的岩质边坡稳定性分析方法可靠性更高。

Rosenblueth法又称概率矩点估计法(以下简称R法)，是由Rosenblueth于1975年提出的一种近似的求多个随机变量矩估计的方法，其基本原理较之改进一次二阶矩阵及蒙特卡洛法要相对简单且应用方便。Rosenblueth法的基本思想：对于状态函数中的各随机变量，利用各变量的均值与方差表示的某些特定的点值，通过状态函数的响应，求得状态函数的各阶矩。通过Rosenblueth法求得各个评价指标，由于Rosenblueth法原理简单、实用性强，对于岩质高陡边坡的稳定性评价可靠性较高。水电站边坡工程具有较强的复杂性及不确定性，利用可靠度理论，应用蒙特卡洛法和改进Rosenblueth法进行水电站边坡可靠性分析。

2 可靠度理论

对于水电站岩质边坡稳定性分析，根据水电站边坡的整体结构特点、失稳破坏机理、岩体力学状态以及环境作用的影响，建立安全系数状态函数，综合考虑黏聚力、内摩擦角、岩石块体结构等随机变量，对于本文中的各随机变量可认为服从正态分布或者对数正态分布，建立状态函数表达式。公式如下：

Z=F(X1，X2，X3，…，Xn)

(1)

式中:X1、X2、X3、…、Xn为水电站岩质边坡的岩体的黏聚力、内摩擦角、密度、水电站泄洪蓄水期水位等边坡力学性质等随机变量，文中的各随机变量可认为服从正态分布或者对数正态分布。

通常影响水电站边坡稳定性的主要依赖于岩体的抗剪强度，即内摩擦角和黏聚力。边坡稳定性方法主要包括极限平衡法、Morgenstern-Price法、不平衡推力法等。文中选取Morgenstern-Price法中边坡安全系数计算方程为状态函数：

作用于条块上的力包括：岩块自重、滑动面的分布水压力和表面荷载如地震荷载，处于蓄水状态的库水对部分条块产生水压力,单独条块主要受条块的自重Gi、外部荷载Wi、条块间法向力Ei及Ei-1、与底面的垂直距离分别是zi及zi-1、水压力Ui、抗剪力Fp、Fs为边坡稳定安全系数，假定法向作用力与切向作用力之间的关系为Y=μg(x)X,μ为力平衡系数及g(x)为岩体条块间法向作用力与切向作用力的关系函数。一般为常值函数或者半正弦函数，则岩体条块间的剪切力为μgi-1Ei-1、μgiEi。Rosenblueth法是一种近似求随机函数数学期望的方法，对于未知分布函数的随机变量，只需要在变量分布区间上取对称点，一般可用整体均值加减标准差，即式(2)确定状态函数取值点：

X1=μx1+σx1

X2=μx2-σx1

(2)

利用概率分布的知识，对于m个相互独立的随机变量，状态函数取值点有2m个，根据所有的取值点与状态函数对应关系，求得2m个状态函数，也就求得2m个安全系数。对于n个随机变量的一般情况，设功能函数可由式(2)表示，其中Xn为对功能函数产生影响的各随机变量。由Rosenblueth方法可以求得功能函数的均值与方差：

(3)

特殊的，对于本文中所确定的随机变量，通过对边坡力学性质的分析，可以认为随机变量是不相关，对于n个相互独立的随机变量，每一取值点出现的概率相等。

(4)

根据中心距与原点矩的估计，可以导出安全系数概率分布的4阶表达式，由此可估计出概率分布的空间形态和位置。如果状态变量存在相关关系，则其相互组合的出现概率不一，出现概率大小应取决于状态变量之间的相关系数，则：

式中：i=1，2,3,...,n；当xi=xi1时，ei=1，当xi=xi2时，ei=-1；φij为变量xi,xj之间的相关系数，则状态函数可以写为：

3 水电站边坡工程算例

水电站边坡位于广东省境内，引水口穿越陡峭山体段，水电站上下游水位界限相距320 m，正常蓄水高程为150 m。从河岸边坡上游往下游170～230 m，为花岗岩露出段，风化侵蚀较为严重，岸坡体较为完整无明显冲沟及裂缝，坡度约40～48°，为高陡岩质边坡；左岸主要岩石为粉质砂岩，岩体较为疏松，坡顶上部有小型裂缝，裂缝宽度约为3～4.2 m，坡度为46～52°，是水电站易发生滑坡的最大危险区域。将Morgenstern-Price法中的抗剪强度参数以及岩体重度作为状态函数的随机变量。水电站边坡安全系数采用Morgenstern-Price法和不平衡推力法共同求解，将滑动面所受的力，按滑动面法向与切向分解，根据力的平衡原理以及力矩平衡方程，得到水电站边坡安全系数如下，计算结果见表1。

(5)

根据不平衡推力法计算岩体条块间法向力：

Ei=Ei-1ζi+FsGh-cili-Gvtanφi

(6)

式中：Ei为第i个条块推力，kN；传递系数ζi=cos(θi-1-θi)-tanφisin(θi-1-θi)；Gh为滑体重量沿滑动面方向分量，kN；Gv为滑体重量垂直滑动面方向分量，kN。

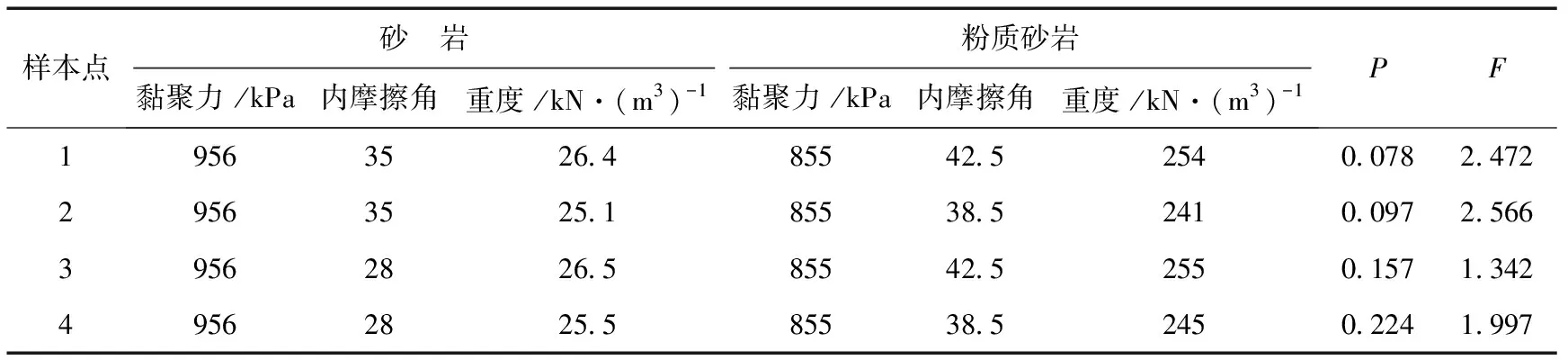
表1 改进Rosenblueth法计算结果Tab.1 Improved Rosenblueth calculation results

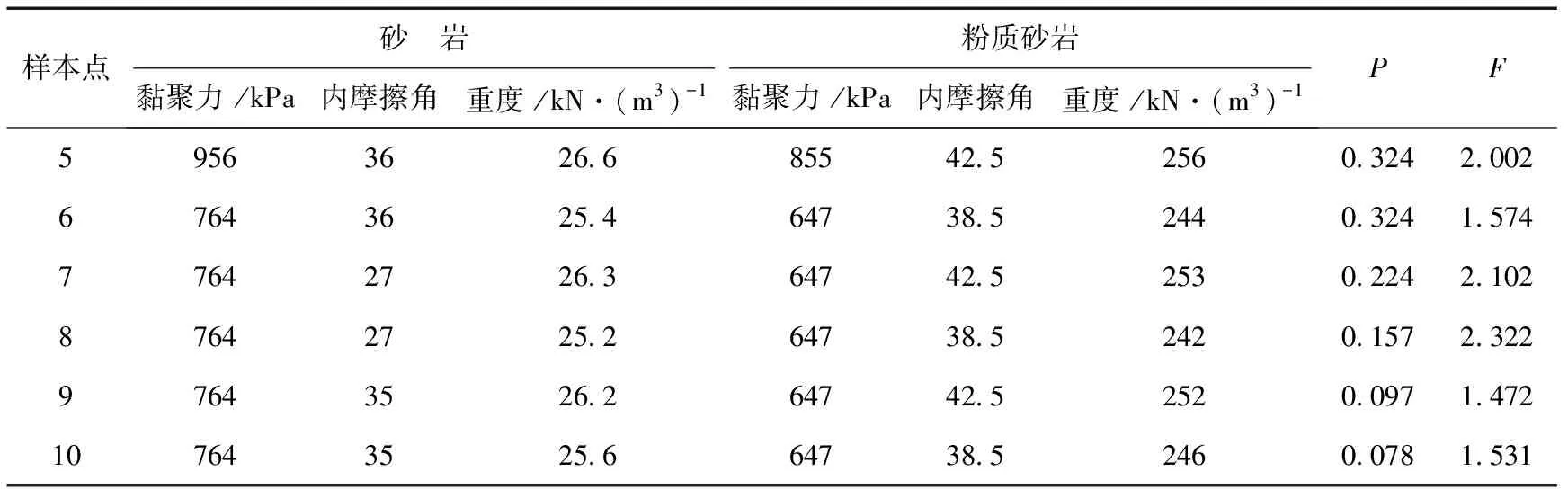
续表1

对于n个相互独立的随机变量，每一取值点出现的概率相等，由于两个随机变量相互独立:

求得状态函数的均值:

状态函数的方差为：

状态函数服从正态分布，则可靠指标为

边坡发生破坏概率为

Pf=1-Φ(β)=1-0.735=26.5%

采用蒙特卡洛法进行对比计算(运行迭代次数为3 000次)，对比结果见表2。

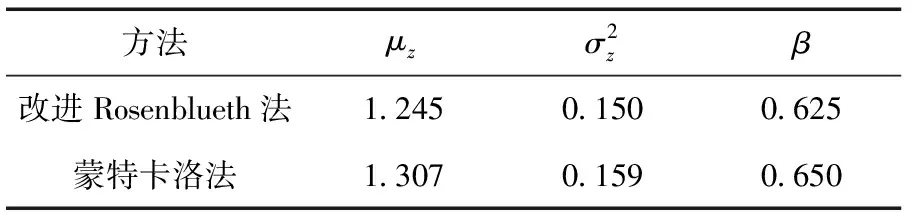
表2 水电站边坡不同计算方法结果Tab.2 Different calculation methods of the slope of the hydropower station results

根据表2可得，改进Rosenblueth法与蒙特卡洛法所求得的状态函数均值、方差、可靠指标最大相差约6%，可以验证改进Rosenblueth法的对水电站边坡分析的有效性。水电站边坡发生滑坡的概率为26.5%。

4 结 论

在岩质边坡稳定性可靠度分析的方法中，改进一次二阶矩法、蒙特卡罗法由于在计算过程中需要对状态函数求偏导，但状态函数往往具有复杂的表达形式，蒙特卡洛还需要多次的迭代，往往出现不收敛的情况，大大降低了两种方法的适用性。通过Rosenblueth方法与蒙特卡洛法求解对比，改进Rosenblueth方法是一种原理简单且计算结果较为精确的方法，对于复杂不宜求偏导的状态函数方程显示较强的适用性。水电站高陡岩质边坡稳定性分析是一项复杂的系统工程，水电站边坡的稳定性具有重要的经济效益、社会效益及环境效益，需要对其进行深入的分析与了解。通过上述分析可知，改进Rosenblueth方法可以作为高陡岩质边坡稳定性分析的一种判据。