基于直线加权平均的平均值法、逐差法和最小二乘法的等效假设研究
魏同利 郝惠娟 马天鹏
(1北方民族大学电气信息工程学院; 2宁夏大学预科教育学院,宁夏 银川 750021)
算术平均值法、逐差法和最小二乘法是常用的3种处理等间距线性数据的方法。但是由于对这3种方法的前提、假设和使用条件的介绍和讨论相对较少,在实验教学和工程应用中出现了一些混乱,误差处理中张冠李戴的现象并不少见。一些作者已注意到该现状,就相关问题写了一系列文章[1-7]。比较具有代表性的,如高永祥[5]认为“普通最小二乘法与加权最小二乘法(逐差法)的前提条件和基本假定是不相同的,不能在相同模型下比较普通最小二乘法和逐差法的优劣,否则,方法和模型会产生矛盾,得出错误结论”,给出不能否定也不能滥用逐差法的论断;吕大韵提出“就其本质而言,逐差法主要是为了减小系统误差的影响”[6]。
现行的研究相对局限在对方法本身“好或不好”的讨论上,而对方法的基本假设及其所处理的“对象(数据)”缺乏系统研究。我们认为每种方法都有其假设的条件,方法是否合用,在于该方法的假设和具体数据之间的贴近程度。数据越贴近所用方法的假设,所得到的结果就越好,其对应的标准误差越小;反之,结果就较差,其对应的标准误差也较大。为了澄清该问题,我们以任意两点所确定的直线为研究对象,针对等间距线性数据,对算术平均值法、逐差法和最小二乘法的基本假设进行了研究,通过确定每条直线在不同处理方法中的权重,对3种方法各提出一种等效假设。由此假设出发,建议了3种数据类型的处理方法: 在标准误差对最小间隔相等的数据类型中,经算术平均值法计算的斜率,标准误差最小;在标准误差对每一点相等的数据类型中,通过最小二乘法计算的斜率,标准误差最小;最后在不等精度的假设下(相当于一种加权平均值法),定量给出了逐差法最优的标准误差分布,测量数据的标准误差由两端向中间区域以1/2次方的速率衰减时,经逐差法计算所得的斜率,标准误差最小。
1 3种线性处理方法的等效假设
设线性数据由2n个等间距的测量点组成,分别为(x1,y1),…,(xi,yi),…(x2n,y2n)。设相邻两点满足Δx1=…=Δxi=…=Δx2n-1=Δx,其中Δxi=xi+1-xi。将相邻两点构成的区间称为一个基本区间,其y值之差可分别表示为Δy1,…,Δyi,…,Δy2n-1,有:Δyi=yi+1-yi。
1.1 算术平均值法的等效假设
算术平均值法可看作任意两点所确定的直线斜率的加权运算。其加权方式可由以下假设确定:
① 最佳直线的斜率由所有基本区间的斜率按照其权重相加;
② 任意基本区间等权。
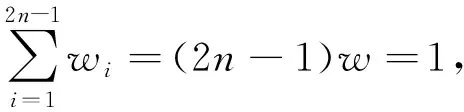
(1)
其中,bm表示该假设下等间距线性数据的最佳斜率,与平均值法的结果是一致的。
1.2 逐差法的等效假设
逐差法同样可以看作任意两点所确定的直线斜率的加权运算。其加权方式可由以下假设确定:
① 最佳直线的斜率由所有可能的包含n个基本区间的直线斜率按照其权重相加;
② 任意包含n个基本区间的两点确定的直线等权。
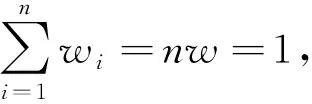
(2)
其中,bz表示该假设下等间距线性数据的最佳斜率,此假设所得到的斜率和逐差法的处理结果是一致的。可求得每一基本区间的权重为
(3)
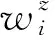
1.3 最小二乘法的等效假设
最小二乘法也可以看作直线的加权运算。其加权方式可由以下假设确定:
① 最佳斜率由所有可能直线的斜率按照其权重相加;
② 直线权重与确定它的两点之间的基本区间个数的平方成正比。
此假设下,由指标为i和j的两点确定的直线的权重可以表示为
Ci,j=(j-i)2w
(4)
其中,w为基本区间即相邻两点所确定直线的权重。在此假设下,等间距线性数据的斜率可计算如下
(5)
按照最小二乘法的计算规则,其斜率可推导如下:
(6)
该假设的基本区间权重系数和最小二乘法计算的结果中都包含有n2-(n-i)2项,由于其他参量与指标i无关,可知此假设是正确的。由式(6)可得任一基本区间的权重
(7)
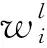
2 最佳斜率的标准误差
2.1 基本区间等权的数据类型
在基本区间的误差满足正态分布且标准误差都相等时,每一基本区间的标准误差为
σ(Δy1)=σ(Δy2)=…=σ(Δyn)=σ
(8)
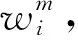
的标准误差平方为
(9)
算术平均值法最佳斜率的标准偏差为
(10)
依据式(3)和式(7),可求得该假设下,逐差法和最小二乘法所求得的最佳斜率的标准误差
(11)
比较式(10)和式(11),可以看出算术平均值法的标准误差最小。
2.2 点等权的数据类型
在每一点的误差满足正态分布且其标准误差相等的假设下,取每一点的标准误差为
σ(y1)=σ(y2)=…=σ(yn)=σ
(12)
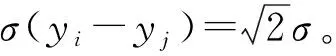
(13)
(14)
应满足最小值条件。任意两条直线的权重满足以下条件
(15)
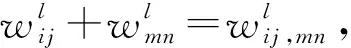
(16)
此权重系数和最小二乘法的基本假设完全相符:任两点确定的直线的权重与其包含的基本区间的个数的平方成正比。所以在点等权的数据类型中,最小二乘法所得的斜率的标准误差最小,其最佳斜率的标准误差为[7]
(17)
依据式(1)和式(2),可求得算术平均值法和逐差法的最佳斜率的标准误差
(18)
可知在点等权的数据类型中,最小二乘法和逐差法最佳斜率的标准误差都与n3/2成反比,而算术平均值法最佳斜率的标准误差与n成反比,故在这种假设下最小二乘法和逐差法远优于算术平均值法。
2.3 逐差法最优的数据类型
我们依据式(1)、式(3)和式(7)绘制了n=16时,3种方法所求最佳斜率的基本区间权重的分布图(图1)。算术平均值法对应基本区间的平权运算;逐差法的权重在中间n指标区域最大,起始和末尾区域的权重最小;最小二乘法在起始、中间和末尾区域的权重介于算术平均值法和逐差法之间。即算术平均值法、逐差法和最小二乘法都可以看作对基本区间的加权运算。
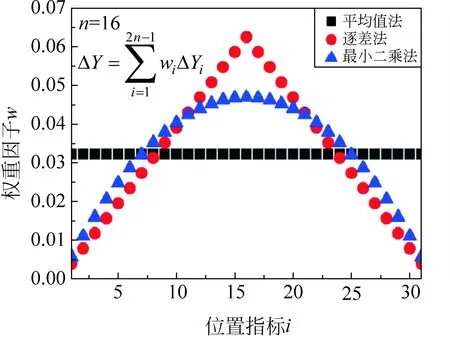
图1 权重因子与位置的关系
由2.1节和2.2节的讨论,在关于斜率的计算中,算术平均值法和最小二乘法都有与其对应的等精度数据类型,分别以算术平均值法和最小二乘法斜率的标准误差最小。但在实际的问题中,等精度假设有时是不能成立的。逐差法的数据类型恰是这样一种不等精度的数据类型。通过式(3)中的权重因子的比较,我们以不同位置基本区间的标准误差为研究对象,给出其标准误差的分布。其论证过程如下:逐差法作为该假设下最优的方法,每一基本区间的权重因子应使得Δy的标准误差最小,即:Δyz=w1Δy1+…+wnΔyn的标准误差最小,其标准误差的平方可以表达为
(19)
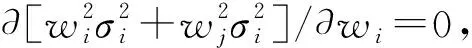
(20)
(21)
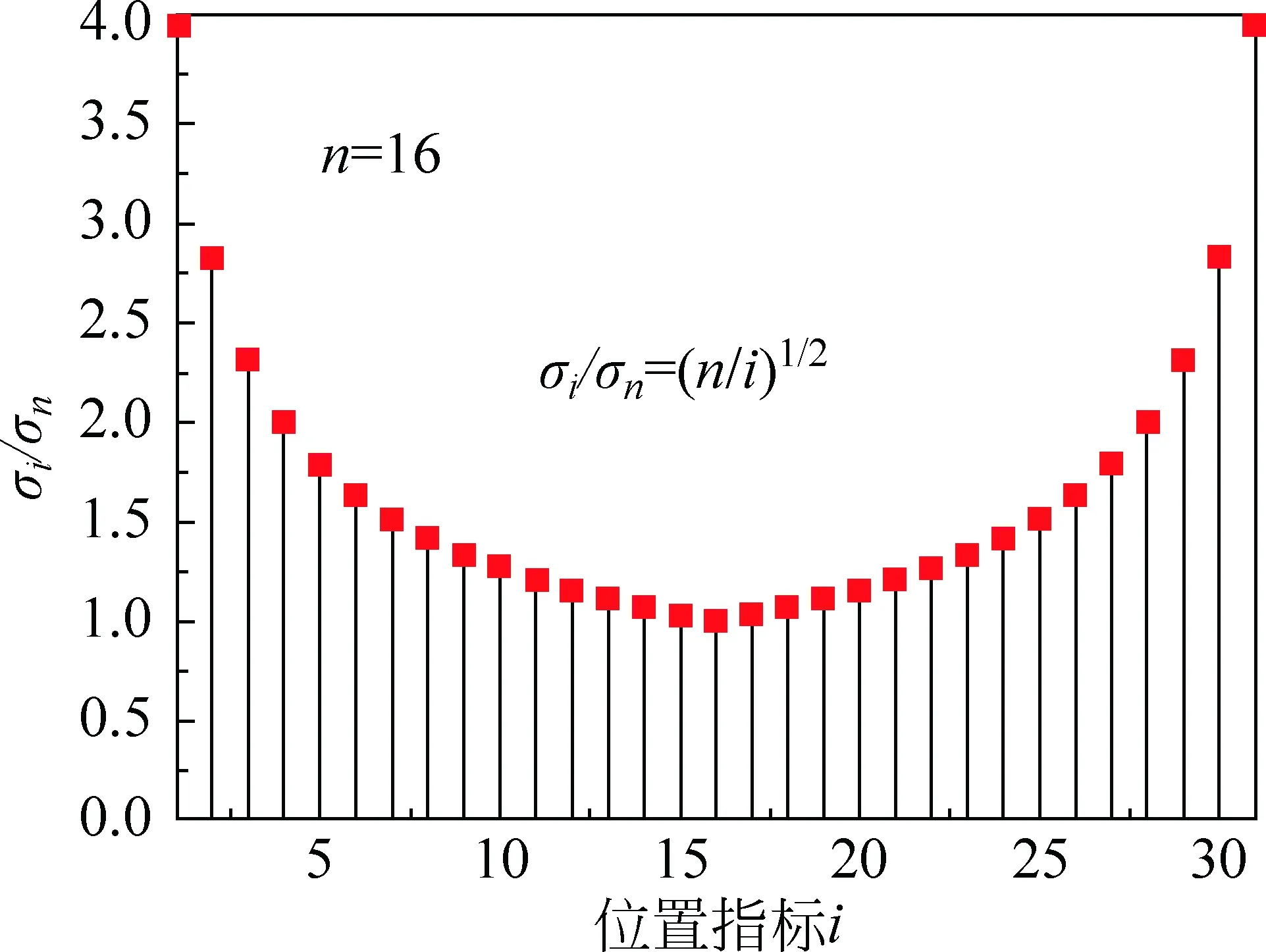
图2 逐差法的标准误差分布
最佳斜率的标准误差为
(22)
3 结论
本文通过直线加权的方式系统考察了处理等间距线性数据的3种方法:算术平均值法、逐差法和最小二乘法。针对3种处理方法各提出一种较为直观的等效假设:算术平均值法只考虑相邻点所确定的直线,并等权地处理它们;逐差法考虑包含n个基本区间的两点所确定的直线,等权的求其平均;最小二乘法则考虑了所有可能直线的影响,其权重与两点之间的距离的平方成正比。
提出以算术平均值法、逐差法和最小二乘法为最优方法的3种数据处理类型:在标准误差对最小间隔等权的数据类型中,经算术平均值法计算的斜率,标准误差最小;在点等权的数据类型中,经最小二乘法计算的斜率,标准误差最小;在不等精度的假设下,定量给出了逐差法最优的数据类型:测量数据的标准误差由两端向中间区域以1/2次方的速率衰减。对于这种两端区域精确度低,中间区域精确度高的线性数据,选用逐差法是较优。在具体的测量中,必须仔细分析误差的性质和来源,以确定线性数据的种类,选用合适的处理方法。
■

