用于齿廓弧面倒棱的挤棱刀廓形设计

□ 崔雪莹 □ 任唯贤

1.中国航发哈尔滨东安发动机有限公司 哈尔滨 150066

2.重庆大学机械传动国家重点实验室 重庆 400044

1 问题的提出

齿轮倒棱能有效避免毛刺损伤齿面，并减小齿轮热处理时的应力集中。齿轮倒棱在一定程度上能降低齿轮啮合噪声，提高齿轮传动精度，延长齿轮使用寿命，是齿轮加工环节中的一道重要工序［1］。 齿轮倒棱分为齿廓倒棱、齿顶倒棱与齿向倒棱，如图1所示。

传统的齿轮倒棱工艺是将棱边加工成45°左右的斜面，但同时会产生新的棱边，无法完全消除棱边处的应力集中问题［2］。在高速重载的高可靠性传动要求场合，有弧面倒棱的要求。弧面倒棱是用圆面或其它二次曲面光滑连接啮合面、上下齿面与齿顶圆面，从而完全消除齿轮的棱边，可以最大限度减小热处理时的应力集中，在极端工况中应用广泛［3］。

弧面倒棱同样分为齿顶弧面倒棱、齿向弧面倒棱与齿廓弧面倒棱，其中齿廓弧面倒棱最复杂，且大多采用手工打磨的方式，生产效率低，加工质量差。可见，实现高效的齿廓弧面倒棱是迫切需求。

▲图1 齿轮倒棱

2 齿廓弧面挤棱工艺

针对齿轮的不同位置，倒棱工艺也不相同。齿顶倒棱一般安排在齿轮毛坯加工阶段，采用车削工艺。齿向倒棱安排在滚齿或磨齿工艺中，通过改变滚刀或砂轮齿根处的廓形加工得到。齿廓倒棱工艺相对复杂，针对不同的工况条件可以选择铣削、磨削、刨削、挤削等加工方式。以下针对齿廓倒棱工艺进行具体分析。

（1）铣棱工艺。采用高速旋转的指状铣刀，沿着齿廓轨迹方向进行铣削，切除待加工棱边。铣棱工艺具有方法简单、刀具通用性强的优点，但加工效率低。此外，为保持刀具强度，铣刀有最小半径的限制要求，导致加工小模数齿轮时在靠近齿根位置会发生干涉。

（2）磨棱工艺。磨棱工艺分为片状砂轮磨与蜗杆砂轮磨［4］。片状砂轮磨的原理与铣棱工艺相同，也是沿齿廓轨迹方向进行磨削，同样存在效率低、加工干涉问题。蜗杆砂轮磨与传统的磨齿工艺类似，磨棱砂轮的齿厚比磨齿砂轮的齿厚大，磨削时只加工端面，不作齿向进给，采用展成原理加工齿廓棱边，效率较高，但是磨棱形状难以控制［5］。

（3）挤棱工艺。采用如图2所示盘状挤棱刀与待加工齿轮强制啮合，挤除齿轮棱边上的多余材料。这样去除材料的方法与传统切削相比，会产生大量飞边，且表面粗糙度值较大。而另一方面，挤棱工艺采用展成原理，效率较高，且不易产生干涉，同时对于内齿轮、锥齿轮等同样适用。挤棱工艺最大的优点是可以改变挤棱刀的廓形，控制挤棱形状，适用于加工复杂的倒棱形式［6］。

综合比较上述多种齿廓倒棱方法，齿廓弧面倒棱最适合采用挤棱工艺加工，挤棱工艺的关键是求解挤棱刀廓形。

▲图2 挤棱刀

3 挤棱刀廓形设计

将挤棱刀廓形看作倒棱后齿轮的共轭齿形，求解这一共轭齿形需要先对齿廓弧面倒棱进行建模，确定倒棱后齿面方程的解析式，再将解析式及法向量代入啮合方程，同时进行坐标变换。

3.1 齿廓弧面倒棱建模

建立倒棱坐标系，如图3所示。倒棱坐标系以齿廓渐开线法线方向为X轴，切线方向为Y轴，竖直方向为Z轴，则X-Z平面组成齿廓渐开线的法平面。在法平面内，齿廓弧面倒棱可看作由无数条圆弧组成，圆弧的起点、终点分别与上端面、齿面相切。X-Y平面是齿轮的端面，在每一端面上，倒棱齿廓又可看作渐开线齿廓沿法线方向的偏移，则倒棱后的齿面（倒棱面）与倒棱前的齿面（渐开面）的关系为：

▲图3 倒棱坐标系

式中：rc为倒棱面的矢量方程；ri为渐开面的矢量方程；L为偏移向量，其大小是倒棱面与原始齿面的水平距离，方向是渐开面的法线方向；Ni为渐开面的水平面法向量。

就圆柱斜齿轮而言，齿面是与竖直面成一渐变角度的螺旋渐开面，该角度用βt表示：

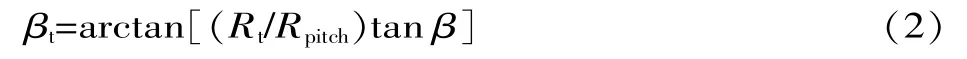
式中：β为齿轮螺旋角；Rpitch为分度圆半径；Rt为齿轮任意一点的半径。

在倒棱坐标系的X-Z平面内，齿廓弧面倒棱的廓形如图4所示。

▲图4 齿廓弧面倒棱廓形

图4中R为圆弧半径；x0与z0分别为圆弧起点与终点的位置，（x0，-R）为圆心坐标。以左齿面为例，由几何关系可得：

圆弧上任意一点的坐标（x，z）为：

式中：α为圆弧的自变量。

则L可看作α的函数L（α），为：

将L（α）与螺旋渐开面方程［xiyizi］T、渐开面水平面法向量［NXiNYi0］T代入式（1），可得到左齿面的倒棱面关于参数α与θ的方程：

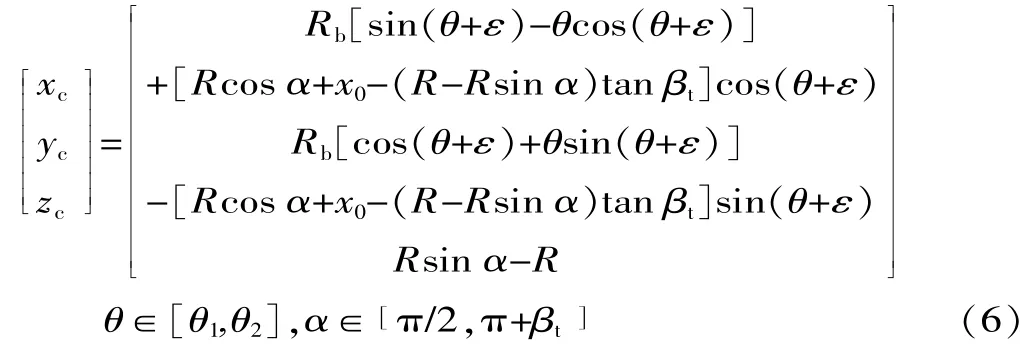
式中：θ1为渐开线的起始展角；θ2为渐开线的终止展角；θ与ε为螺旋渐开面方程的参数，且ε为关于α的函数。

定义螺旋参数k=tanβ/Rpitcn，则Z轴坐标zc=ε/k，同时zc=Rsinα-R，解得：

右齿面的齿廓弧面倒棱同理，由几何关系得：

圆弧上任意一点的坐标（x，z）为：

将L（α）与螺旋渐开面方程［xiyizi］T、渐开面水平面法向量［NXiNYi0］T代入式（1），可得到右齿面的倒棱面关于参数α与θ的方程：

式中：γ为分度圆上左右齿面之间的转角。

根据式（6）、式（11），可在 MATLAB 软件中建立齿廓弧面倒棱模型［7］，如图 5所示。

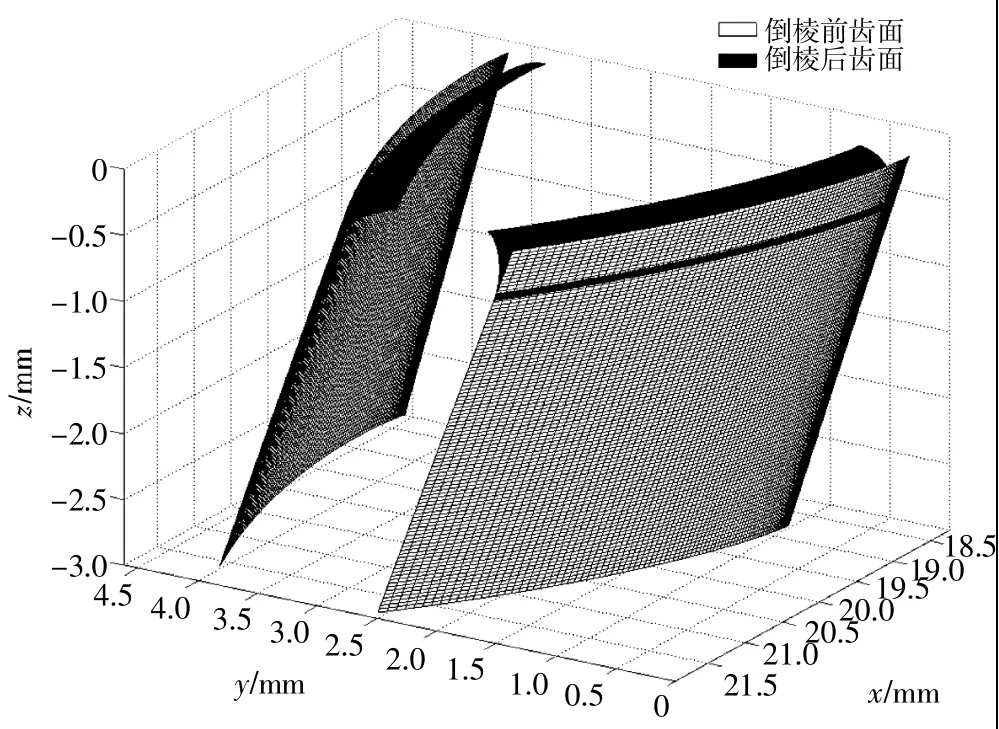
▲图5 齿廓弧面倒棱模型

3.2 挤棱刀廓形计算

求解挤棱刀廓形时采用齿 廓法 线法［8］。挤棱刀与齿轮的啮合关系相当于两个直齿外齿轮的平行轴传动，建立齿轮与刀具坐标系，如图6所示。

设S1-X1Y1为与齿轮固连的齿轮坐标系，S2-X2Y2为与挤棱刀固连的刀具坐标系，Sp-XpYp与Sf-XfYf为固定的辅助坐标系，ρ1、ρ2分别为齿轮与刀具的节圆半径，φ1、φ2分别为某一瞬时齿轮与刀具转过的角度，则中心距E=ρ1+ρ2，传动比n=φ2/φ1。 令m=1+n，则φ1+φ2=φ1+nφ1=mφ1。

▲图6 齿轮与刀具坐标系

挤棱刀的齐次坐标矩阵r2可表示为：

式中：r1为倒棱面的齐次坐标矩阵；T21为S1-X1Y1到S2-X2Y2的坐标变换矩阵；T2p为Sp-XpYp到S2-X2Y2的坐标变换矩阵；Tpf为Sf-XfYf到Sp-XpYp的坐标变换矩阵；Tf1为S1-X1Y1到Sf-XfYf的坐标变换矩阵。

根据坐标变换式［9］，有：

计算转角φ1与φ2时，需要借助齿轮啮合原理方程［10］：

法向量经坐标变换后有：

根据式（6）、式（11），可以求得左右倒棱面的法向量［11］：

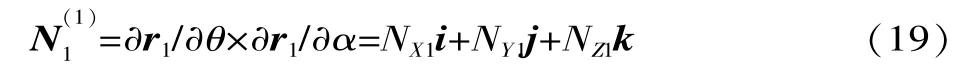
式中：i、j、k依次为X轴、Y轴、Z轴的单位矢量。

式中：ω为角速度。

将式（18）、式（20）代入式（17），求解方程即可得到φ1，再将φ1、φ2=nφ1代入式（16），求解T21，并代 入 式 （12），最 终 求得挤棱刀廓形。在MATLAB软件中绘制挤棱刀廓形，如图7所示。

将计算得到的挤棱刀廓形导入三维绘图软件，生成曲面特征，同时结合毛刺刮盘、刀体与刀架的连接等结构设计，最终得到弧面挤棱刀，如图8所示。加工时挤棱刀与齿轮相啮合的工作面如图9所示，需要说明的是，笔者只针对挤棱刀工作面的廓形进行设计，并不涉及变位距离、刀具后角、刀具根隙等。

▲图7 挤棱刀廓形

▲图8 弧面挤棱刀

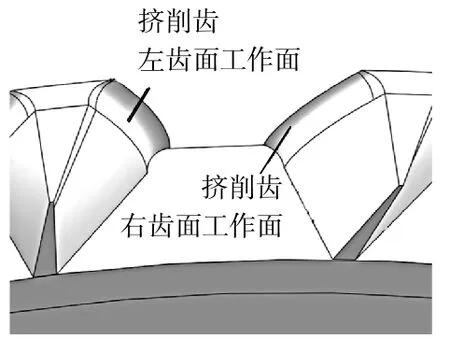
▲图9 加工时工作面

4 结束语

齿廓弧面倒棱可以实现齿面与端面的光滑过渡，笔者提出了挤棱刀加工齿廓弧面倒棱的方法，通过齿轮啮合原理，计算并设计出挤棱刀工作区域的廓形，为下一步进行完整的挤棱刀设计打下了基础。设计出完整的挤棱刀，可以在一定程度上解决当前齿廓弧面倒棱仍靠手工打磨的问题，提高加工效率与倒棱质量，降低企业的生产成本。