汽轮给水机组液压调节系统动态特性研究
倪 平,江 攀,蔡佐君,刘克成
(上海船舶设备研究所,上海 200031)
0 引言
汽轮给水机组在蒸汽系统中是非常重要的一种辅助设备,它运行是否稳定直接影响到整个系统能否稳定有效地工作。调节系统在机组运行中发挥着至关重要的作用:当机组受到外界干扰时,调节系统能够减小干扰对机组的影响,维持机组的稳定运行;当蒸汽系统需要改变工况时,调节系统可以及时调整机组工况满足锅炉对给水流量和水位的要求。因此,开展对调节系统动态特性的研究,掌握其规律特性是十分必要的一项工作[1-7]。
给水泵调节方式可采用定转速调节或变转速调节,某蒸汽系统使用变转速汽轮给水机组控制锅炉给水,调节方式为机械液压调节,调节方式为压差调节,如图1所示。

图1 调节原理图
调节系统的关键部件是压差调节器,调节系统简图如图2所示。调节系统的工作方式为:压差调节器使用水作为工作介质,初始时波纹管感受给水调节阀前后压差信号,通过压差调节器杠杆使控制阀挡板处于中间位置,高压水进入压差调节器后经过2个小孔输出压力相等,即汽轮机调节阀活塞前后压差为零,活塞保持平衡,机组稳定运行。
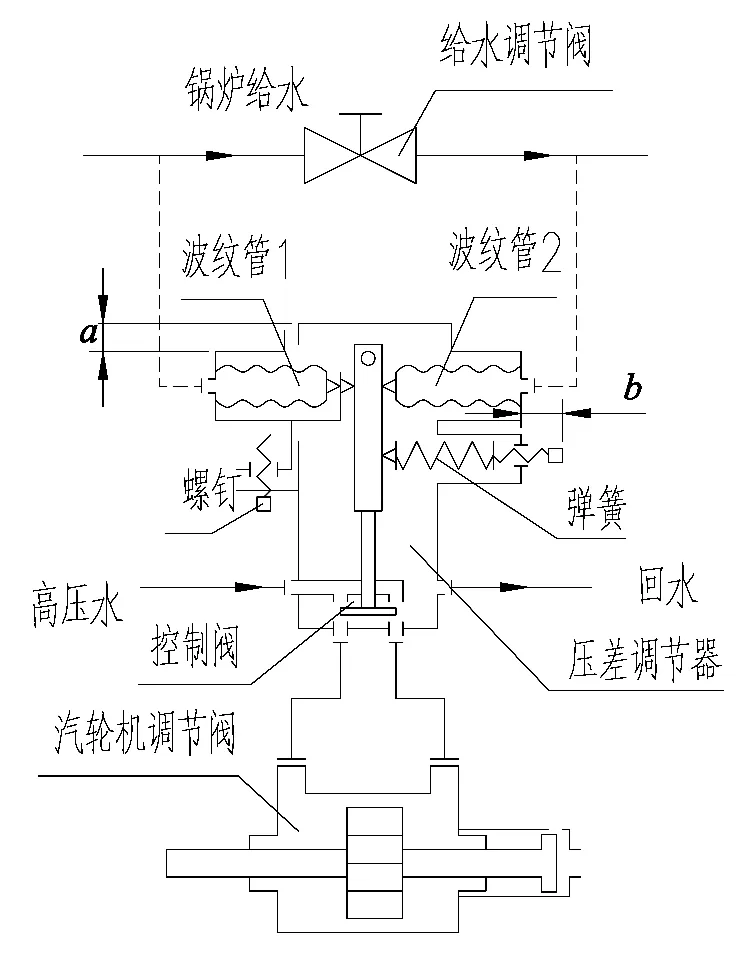
图2 调节系统简图
当给水调节阀前后压差减小,杠杆由于波纹管的作用顺时针旋转,右边小孔流量增加,接受孔内水压变大,推动汽轮机调节阀活塞向左移动,打开调节阀,提高转速,使给水泵出口压力升高,从而恢复压差,反之活塞向右移动。通过调整螺钉和弹簧(改变尺寸a和b)可以整定压差调节器的压差特性,使其满足使用要求。
为便于开展动态特性研究,需对调节系统中各个环节建立数学模型。
1 数学模型
1.1 容积方程
对汽轮机调节阀有蒸汽容积方程

式中:T1为时间常数,s;P1为蒸汽压力变化Δp对初始压力p0的相对值,;E为调节阀开度变化ΔZ1对初始开度Z0的相对值,
根据计算可得T1=0.1 s,因此容积方程传递函数为

1.2 转子方程
汽轮给水机组轴系为多转子系统,包括汽轮机转子、减速器转子、给水泵转子、凝水泵转子以及增压泵转子,将减速器转子等效至汽轮机转子后,转子方程为
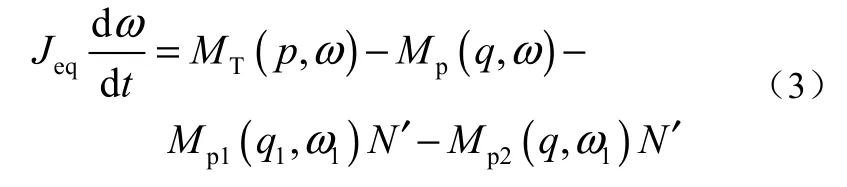
水泵反力矩与进出口压差Δpp、质量流量qp、角速度ωp和效率ηp之间的关系为

根据给水泵、增压泵和凝水泵数据,并将其做线性化处理后,可以获得各水泵的反力矩方程,为

将上述反力矩方程以及各参数代入汽轮机转子方程式(3)可得

式中:Ta为转子的飞升时间常数,s。经计算可得Ta=3.5 s。因此,汽轮机转子传递函数为

1.3 给水调节阀方程
根据给水调节阀特性数据,可得给水调节阀方程,为
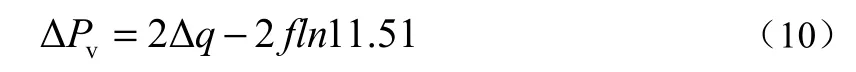
式中:ΔPv为给水调节阀前后压差ΔP4变化的相对值,;f为开度 L变化的相对值,
1.4 管路方程
使用水泵特性数据,并做线性化处理后可得给水泵特性。

式中:ΔP3为给水泵出口压力变化相对值,ΔQ为给水泵流量变化相对值,
给水泵出口至锅炉之间的管路方程为(忽略锅炉水位高度的影响)

式中:Pb为锅炉压力,Pa;ΔPl为管路阻力压力损失,Pa;l为给水泵至锅炉进口管路长度,m;Ag为管路截面积,m2。
根据给水调节阀方程式(10)、给水泵方程式(11)以及给水泵出口管路特性(12)得管路方程式为
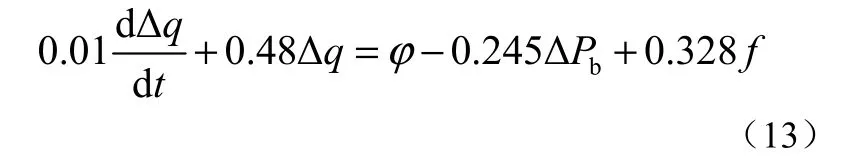
从而得到传递函数

1.5 管路压力平衡方程
由给水调节阀阀后压力与锅炉压力平衡可知(忽略锅炉水位高度的影响)

式中:p5为给水调节阀阀后压力,Pa;Δpl′为管路阻力压力损失,Pa。
由阻力特性计算并经过线性化得管路压力平衡方程为

1.6 压差关系方程
给水调节阀前后压差为

无量纲方程为

取p40=1.7 MPa,p50=6.9 MPa,得

1.7 压差调节器方程
压差调节器主要工作零部件为波纹管、杠杆和喷嘴挡板,分别对上述零部件开展分析,建立压差调节器模型。
压差调节器波纹管示意图如图3所示。
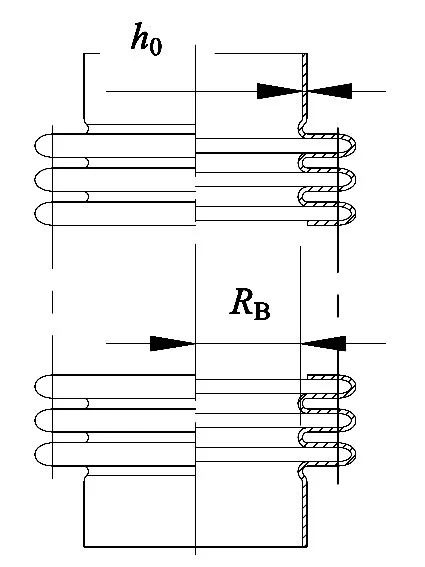
图3 波纹管示意图
波纹管中产生的力为

式中:FB为波纹管受力,N;Pe为波纹管压力,Pa;Ae为波纹管有效面积,m2。
压差调节器杠杆示意图如图4所示。

图4 杠杆示意图
杠杆转动角度θ时,有力平衡方程为
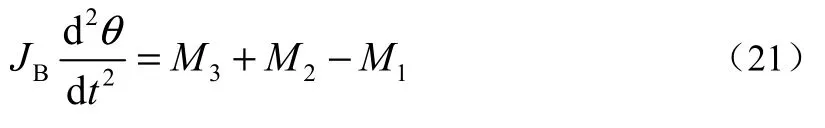
式中:JB为杠杆转动惯量,kg·m2;M3为弹簧力矩,N·m;M2为波纹管 1(见图2)的作用力矩,N·m;M1为波纹管2(见图2)的作用力矩,N·m。
由图4和式(21)可得


根据结构尺寸参数计算,可得杠杆方程为
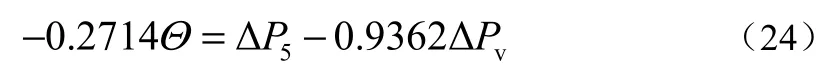
喷嘴挡板与调节阀联动示意如图5所示。
建立调节阀活塞力平衡方程,为
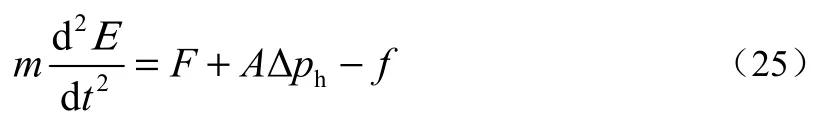
式中:m为活塞和阀杆的质量,kg;E为调节阀阀杆位移,m;FZ为蒸汽力,N;f为阻力,N,根据实测,此力较小,忽略不计;A为调节阀活塞面积,m2;ΔPh为活塞上下压差,Pa。
经计算,活塞方程时间常数仅为0.000 19,因此活塞方程可忽略不计。
喷嘴挡板如图6所示。

图5 喷嘴挡板与调节阀联动示意图
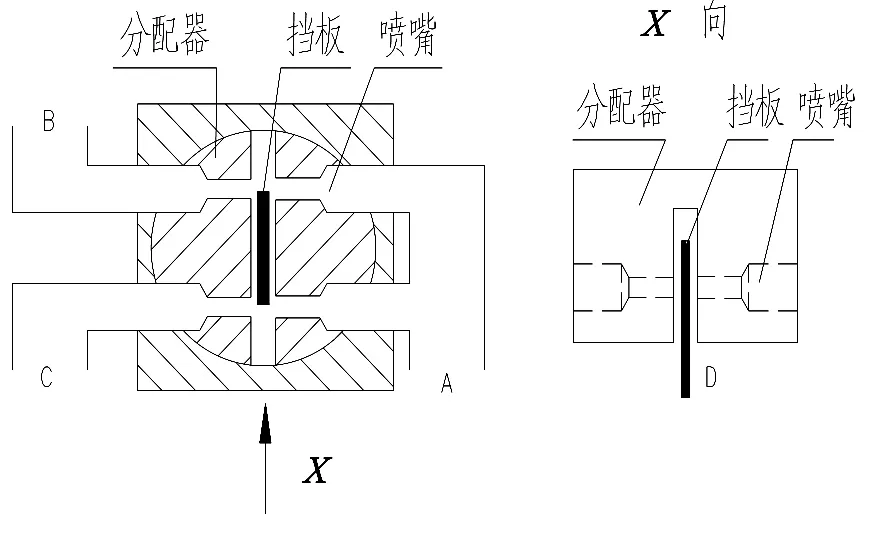
图6 喷嘴挡板示意图
工作水在喷嘴挡板处流动情况:工作水从A口进入,经过喷嘴,部分水从B口和C口进出调节阀活塞腔室,其余水从D口流出。
由图5可知:调节阀阀杆向下移动时,工作水从B口流入调节阀活塞上部腔室,调节阀活塞下部腔室工作水从C口流出,此时建立B口与C口的面积变化关系和流量方程,为


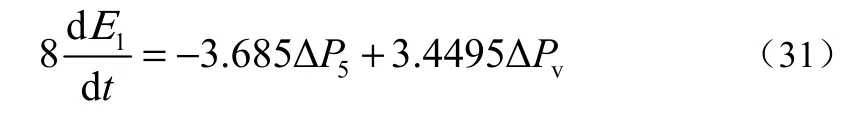
式(19)带入式(31)可得压差调节器方程,为

传递函数为

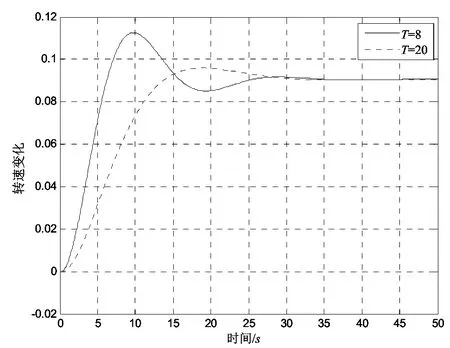
图7 机组转速变化(蒸汽压力扰动)
从图8可以看到:当给水调节阀发生扰动时,比较调节阀在时间常数8和时间常数20的变化,两者几乎同时趋于稳定,但前者超调量较大,飞升时间上则前者较短,大约比后者短8 s,这有利于满足机组快速起动的需求,可在较短时间内使工况达到要求。时间常数为8的情况下,20 s左右转速波动小于0.5%;时间常数为 20的情况下,转速波动小于 0.5%,大约在21 s左右,这与时间常数为8时基本一致。
当全行程时间为20 s时,压差调节器方程为

传递函数为

2 仿真计算
调节阀全行程时间为8 s和20 s时,在蒸汽压力扰动10%和给水调节阀扰动10%情况下,分别进行仿真计算,结果如图7和图8所示。
从图7可以看到:当蒸汽压力发生扰动时,调节阀时间常数8相比时间常数20更快趋于稳定,但这一优势并不明显,超调量也相对时间常数20时较小。时间常数为8的情况下,大约46 s时稳定,17 s左右转速波动小于0.5%;时间常数为20的情况下,在50 s时转速仍有轻微的波动,转速波动小于0.5%,大约在17 s左右,这与时间常数为8时基本一致。

图8 机组转速变化(给水调节阀扰动)
3 结论
本文通过建立调节系统中各个环节的数学模型,使用传递函数法对系统动态特性进行了研究,掌握了建模和仿真分析的方法,获得了调节阀不同时间常数下的动态特性曲线。通过仿真可知:1)目前调节阀时间常数在 8~20范围内可满足运行要求;2)通过改变调节阀全行程时间可改变动态特性。鉴于运行时对机组动态特性有快速性的需求,应尽量使调节阀时间常数减小,但是同时必须考虑调节阀时间常数较小带来的超调量增加的矛盾,需通过调试获得较佳的调节阀时间常数。本次研究为后续深入开展调节系统的研究奠定了基础,也为调节系统调试提供了参考。

