交通荷载作用下水中悬浮隧道动力响应分析

蒋博林，梁 波

(1.重庆交通大学土木工程学院，重庆 400074；2.重庆工程职业技术学院，重庆 402260)

近年来，对水中悬浮隧道(Submerged Floating Tunnel，SFT)在各种荷载作用下的动力响应分析取得了丰硕成果，但研究悬浮隧道在内部交通荷载作用下动力响应的文献较少。MARTIRE[1]以固定均布荷载的方式模拟交通荷载，研究锚索不同布置形式下悬浮隧道的动力响应。TARIVERDILO等[2]将悬浮隧道中的交通荷载模拟为沿管体纵向移动的集中力，并在此基础上研究了移动荷载激励下悬浮隧道的动力响应。董满生等[3]将交通荷载简化为一系列等间距移动的集中荷载，建立了悬浮隧道动力学模型，并分别研究了张力腿竖向刚度、交通荷载、行车间距对悬浮隧道动力响应的影响；项贻强等[4]建立综合考虑流体-悬浮隧道-车辆系统耦合振动的理论模型，以研究移动荷载作用下系统的动力响应机理及减振措施，并制作了冲击荷载作用下悬浮隧道动力响应整体试验模型；梁波等[5]采用移动振动荷载模拟悬浮隧道中的交通荷载，通过数值模型对比分析不同交通荷载作用下悬浮隧道结构的振动响应，得出采用移动振动荷载更适合模拟悬浮隧道中的交通荷载，但未对交通荷载中所涉及的计算参数进行分析。本文采用移动振动荷载模拟悬浮隧道中的公路交通荷载，采用数值模拟分析和正交试验，分析交通荷载计算参数对悬浮隧道结构跨中振动位移的影响。

1 交通荷载模拟表达式

文献[5]中提出移动振动荷载表达式，其形式为

式中:F(t)为移动振动荷载；P0为车轮静载，代表交通荷载的静载部分；M0为车辆的簧下质量，反映车辆特性；A1是路面不平度，反映路面状况；A2是由波流作用引起的隧道结构振动位移，反映外部激励荷载的影响；ω1是由路面不平度引起的车辆振动圆频率，ω1＝2πvc/L，vc为汽车的运行速度，L为几何不平顺曲线的波长，取车身长；ω2是波流作用下悬浮隧道结构涡激振动引起的车辆振动圆频率，近似取为涡激振动频率，ω2＝2πSrvf/D，Sr为 Strouhal数，通常取 0.2[6]，vf为水流速度，D为管体截面宽度。

该移动振动荷载考虑交通荷载的波动性和周期性，并同时考虑了悬浮隧道结构外部激励荷载中波流荷载对交通荷载的影响。本文拟采用此表达式模拟悬浮隧道中的交通荷载。

2 数值模拟分析

2.1 悬浮隧道结构数值模型

根据文献[7-8]对悬浮隧道的数值模拟分析，本文选取断面形式为圆形、支撑系统为倾斜锚索的悬浮隧道结构进行建模。设悬浮隧道顶部距水面20 m，底部距水底30 m。模型如图1所示。

选取悬浮隧道中的一节管段(100 m)进行计算，管段材料采用钢筋混凝土。锚索布置在距管段两边端头25 m处，仅承受拉力，锚索假定为高强度钢绞线。数值模拟计算基本参数见表1。

图1 悬浮隧道模型(单位:m)

表1 数值模拟计算基本参数

数值模拟计算采用有限元分析软件ANSYS。模型中的荷载主要考虑悬浮隧道内部的交通荷载与外部的波流荷载。交通荷载仅考虑公路交通荷载，采用式(1)中的移动振动荷载F(t)模拟悬浮隧道中的交通荷载，并假定交通荷载以面荷载形式均匀分布加载到悬浮隧道路面两端[9]。计算过程中模拟的交通荷载随时间变化向另外一端匀速移动。假定波浪为Airy线性波，水流为定常流，沿图1中的x方向匀速流动。

2.2 交通荷载计算参数

交通荷载的计算参数主要包括车辆轮载、路面不平度、行驶速度以及外部激励荷载中的波流荷载。研究交通荷载的不同计算参数对悬浮隧道结构动力响应的影响。各参数取值如下:

车辆轮载:小客车、中型车、大型车；

路面不平度:2，4，6 mm；

行驶速度:40，60，80 km/h；

波流荷载:轻浪、中浪、大浪。

2.3 计算结果分析

选取管段跨中节点的竖向位移(y方向)作为悬浮隧道动力响应的分析指标。根据JTG D70—2004《公路隧道设计规范》[10]，隧道内限速80 km/h，由此计算得到车辆通过100 m管段的时间为4.5 s，因此计算中时长取4.5 s。

首先计算无交通荷载作用时悬浮隧道结构的跨中竖向振动位移，同时确定波流作用引起的隧道结构振动位移A2，见图2。为安全起见，取最大值。

其次计算施加交通荷载后悬浮隧道结构的跨中竖向振动位移。在计算时，确定交通荷载中的三项计算参数，只改变另外一项计算参数。由于施加的交通荷载相对于悬浮隧道自重以及其他荷载数值非常小，计算参数的改变引起的结构竖向振动位移的变化较小，因此在图3中将跨中竖向振动位移差别较大的部分进行了放大，以便观察其变化规律。

图2 波流荷载作用下跨中竖向振动位移(无交通荷载)

图3 竖向位移时程曲线

从图3(a)—图3(c)可以看出:①交通荷载计算参数中波流荷载(轻浪)不变，其他计算参数(车辆轮载、路面不平度、行驶速度)的改变对悬浮隧道结构跨中竖向振动位移的影响非常小。②取不同计算参数时跨中竖向振动位移曲线非常接近。相对而言，车辆轮载对跨中竖向振动位移的影响稍大，其次是路面不平度，行驶速度影响最小。

从图3(d)中可以看出:波流荷载的改变对悬浮隧道跨中竖向振动位移的影响较大，但与无交通荷载作用时(参见图2)相比，不同波流荷载作用下跨中竖向振动位移变化曲线基本上无变化。两者均呈波动性变化，且规律不明显。总体来说，波流荷载越大，其引起的结构竖向位移也越大。相比其他计算参数，波流荷载对悬浮隧道跨中竖向振动位移的影响最大。

3 正交试验

3.1 正交试验设计及计算

正交试验目的是为了得到各影响因素对悬浮隧道结构动力响应的影响程度的排序。

根据上文数值模拟分析中选取的交通荷载计算参数进行正交试验，共进行9次试验。采用L9(34)正交试验表进行设计，见表2。

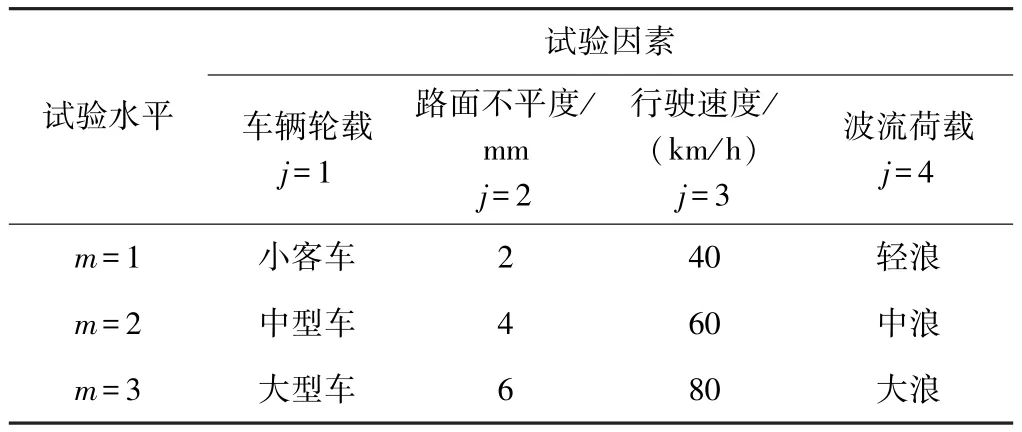
表2 正交试验4因素3水平

确定正交试验的各因素和各水平后，按照正交试验方案，采用式(1)计算交通荷载，采用数值模拟分析中建立的有限元模型计算各试验工况的跨中竖向振动位移。将跨中竖向振动位移作为试验指标。正交试验方案及计算结果见表3。

表3 正交试验方案及计算结果

3.2 正交试验结果分析

根据表3中的正交试验结果，对各试验因素进行极差分析，结果见表4。可以看出，波流荷载的极差相对较大，表明当波流荷载水平波动时，试验指标的变化幅度较大。其余三项试验因素的极差都较小且接近，说明这三项试验因素水平波动时，试验指标的变化幅度非常小。按照极差排序，各试验因素对悬浮隧道跨中竖向振动位移的影响程度由大到小依次为波流荷载、车辆轮载、路面不平度、行驶速度。波流荷载仍然是影响悬浮隧道竖向振动位移响应的重要因素，与数值分析结果相吻合。

表4 极差分析结果

4 结论

1)振动移动荷载考虑了交通荷载的波动性和周期性，并同时考虑了悬浮隧道结构外部激励荷载中波流荷载对交通荷载的影响，适于模拟悬浮隧道内部的交通荷载。

2)数值模拟结果表明，波流荷载的变化能引起悬浮隧道跨中竖向振动位移产生较大的波动，而车辆轮载、路面不平度和行驶速度的改变对悬浮隧道跨中竖向振动位移的影响非常小，说明波流荷载是影响悬浮隧道跨中竖向振动位移的关键因素。

3)正交试验结果表明，各试验因素对悬浮隧道跨中竖向振动位移的影响程度从大到小依次为波流荷载、车辆轮载、路面不平度、行驶速度。波流荷载仍然是影响悬浮隧道跨中竖向振动位移的重要因素，而其他三项试验因素的极差值较小且接近。