基于立体像对与SFS相结合的三维重建研究
杨鸣新,陈 喆,陈 镇
(1.武汉市房产测绘中心,湖北 武汉430015;2.长江科学院 空间信息技术研究所,湖北 武汉 430010)
立体视觉进行三维重建的核心内容是同名点提取和匹配,同名像点匹配后可估计影像的左右视差和上下视差,进而计算得到影像上每一点的三维坐标。传统立体视觉理论基于特征点匹配算法,对于非特征点区域无法进行处理;同时,立体视觉是基于高度重叠的影像,要求特征点同时存在于两幅图像上,对于非重叠区域该方法失效。在影像透视收缩严重时,完全基于影像灰度和纹理结构的匹配方法匹配精度降低。
单幅图像恢复表面形状(Shape from shading,简称SFS)理论[1-3]基于假设的光照模型和物体表面反射模型建立图像的反射图方程,仅靠单张数字影像就可以恢复物体表面的形状信息。许多研究人员将立体视觉与SFS结合起来解决三维重建问题,用立体视觉恢复高频部分、SFS方法恢复低频部分信息。Frankot和Cheelappa[4]首先根据立体视觉原理找到稀疏同名像点并配准,计算该点的高度值,这些特征点的高度值作为SFS算法的初始值;然后用迭代的SFS方法恢复格网点高度。Samaras等人[5]在立体视觉匹配算法中采用最小决策长度(Minimum Description Length,简称MDL)作为相似性测度,在非边缘点区域匹配误差较大。Jin等人[6,7]提出基于变分法,同时估算朗伯体表面的形状、反射率、光源方向,该方法需要稳定的收敛算法来保证解的正确性。Haines和Wilson[8]采用马尔科夫随机场将SFS与立体视觉结合起来;Chow和Yuen[9]提出基于朗伯体表面,将SFS和立体视觉结合起来,用较少的特征点进行匹配并计算深度信息。本文在文献[10]基础上,采用更为稳定的ASIFT算法提取影像特征点,以该点为中心的局部区域进行SFS重建,基于重建的高度值计算相似性测度,并进行全局搜索匹配。将影像上的特征点区域和非特征点区域分开,进行分区处理,采用不同的方式进行三维重建:特征点区域采用立体视觉方式,而非特征点则采用FSM-SFS方法。
1 算法流程
算法流程如图1所示。

图1 立体视觉与SFS结合的三维重建算法流程
假设:①光源为倾斜光源;②物体表面遵循朗伯体表面模型;③基于透视投影假设。令输入图像为Il(u,v)和Ir(u,v),其中(u,v)表示图像二维坐标。对于任意光源影像,需要进行几何变换预处理,使其满足垂直平行光源条件。变换后影像为I'l(u',v')和I'r(u',v');SFIT算子作为经典的检测与描述图像局部特征的方法,具有良好的平移旋转不变性,但当影像有较大倾斜角度时,该方法同名点提取数量不足。ASFIT(Affine-SIFT)算法是SIFT算法的改进,解决了倾斜影像中特征点匹配只能提取很少量特征的问题。为适应不同的影像拍摄角度,本文采用ASIFT算法提取左右影像的特征点集{Pi}和{Qj}作为候选点,并通过透视投影下的Lax-Friedrichs FSM-SFS方法重建特征点邻域三维表面。以特征点集{Pi}和{Qj}为中心的表面区域深度作为相似性测度,进行全局搜索匹配,具有最大相似性形状和深度测度的点被认为是同名像点。确定了同名像点后,根据核线几何计算该点深度值,再运用Lax-Friedrichs FSM-SFS方法获取左右图像的深度图Z'l(u',v')和Z'r(u',v'),对左右深度图进行几何逆变换,并融合得到重建结果Z(u,v)。
1.1 几何变换
令Cc表示相机坐标系,其位置为U,方向为R,则:

式中,Pw和Pc分别为Cw和Cc上的点的三维坐标。令相机焦距为常量f,朗伯体表面的SFS亮度方程可写为:

式中,L表示统一光源方向。设光源坐标系为ls,图像在旋转之后Z轴与光源照射方向重合,则:
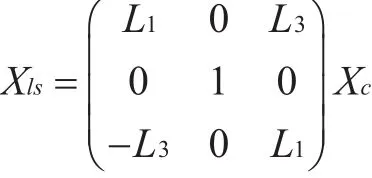
将坐标点投影到光源坐标系下,其坐标为:

点(u,v)和(u',v')一一对应,由于I(u,v)=I'(u',v'),可得到在平行投影下的新影像,影像上物体深度Z的方向与光源方向一致。
1.2 FSM-SFS
为保证SFS解的稳定性,基于传播方法重建出来的三维表面将作为最小化算法的初始值,对表面进行二次重建。将平行光源投影下朗伯体表面的亮度方程写为Eikonal方程形式,则:
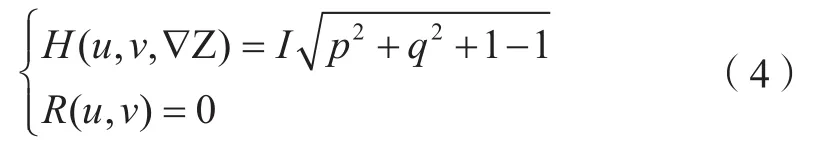
式中,令Zx=p,Zv=q,影像边界点初设为0,对该方程进行离散化表示。本文采用Lax-Friedrichs函数进行离散化,得到数值解迭代公式:

式中,h表示图像的空间分辨率;σu和σv是粘性因子,满足条件:
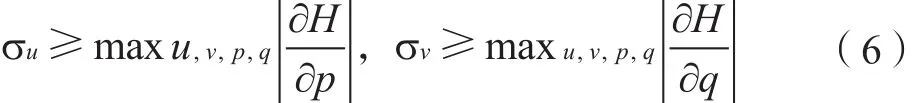
1.3 利用深度信息的相似性测度
将同名核线附近的特征点作为候选点,以特征点为中心获取匹配窗口,在核线距离阈值范围内进行全局搜索。利用SFS算法恢复的特征点附近的局部三维作为相似性测度,以规避左右影像中的透视收缩问题。
对于待匹配点P和Q,首先利用Lax-Friedrichs FSM-SFS进行三维重建,生成两个三维表面HP和HQ,HP和HQ的边界可通过寻找凸表面集合来确定。两个表面的深度的平均差异,即所有点的深度值差的平均值作为匹配过程中相似性测度进行全局搜索,平均差异最小的区域中心特征点即为匹配点。
2 实验分析
采用嫦娥1号(CE-1)拍摄的月球三线阵全色影像作为实验影像。嫦娥一号卫星从面阵CCD上读取第11、512和1 013行阵列以形成三线阵推扫影像。CCD每列线阵像元为512列,相邻线阵之间的视角差为16.7°。实验区域的三线阵影像如图2所示,其中a、b、c分别表示前视、中视、后视影像。

图2 CE-1三线阵截取影像
采用ASIFT提取特征结果如图3。
对每个特征点的邻域区域进行FSM-SFS三维重建,采用深度测度算子进行特征点搜索匹配。匹配结果如图4所示。

图3 ASIFT提取的左右片特征点

图4 ASIFT函数特征匹配结果
由图4可看出,提取出的配准点集中在月坑边缘线上,平滑区域如左图的左上角、右图的右下角区域,基本无配准点。由于三线阵影像隶属于同一面阵CCD,可以认为不同影像上的同名点基本无横向视差,主要存在纵向视差。根据每一对配准点的平面坐标得到计算其视差以及该点的深度信息。
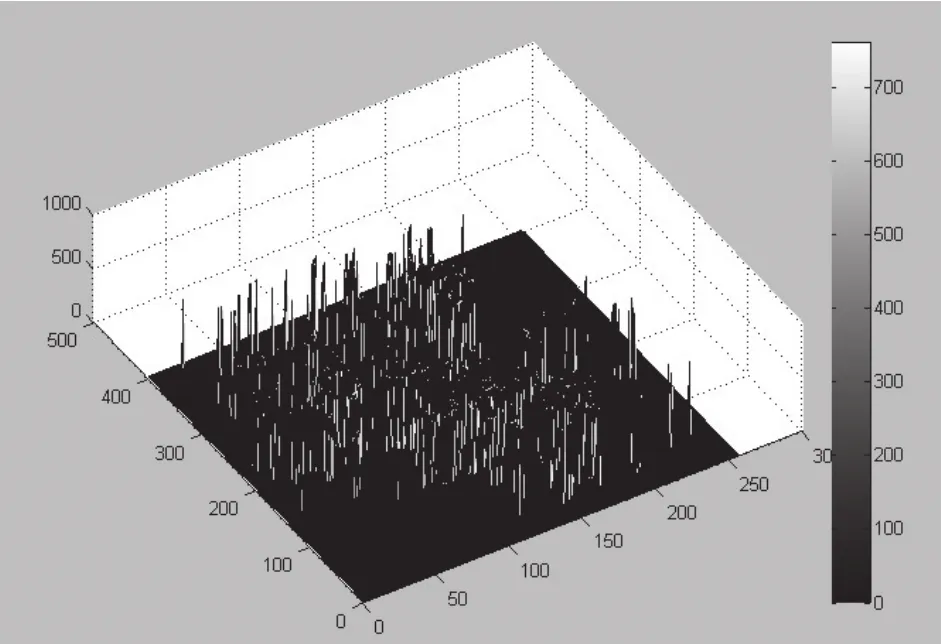
图5 特征点恢复的高度值
对特征点以外的像素点进行单幅影像三维重建恢复表面,最终得到中视影像的三维表面图(图5),并与传统最小化SFS方法的重建结果对比,如图6所示,其中a、c为本文方法和最小化SFS恢复的深度图,b、d为其三维显示。
两种方法精度见表1。

表1 不同方法恢复表面三维精度
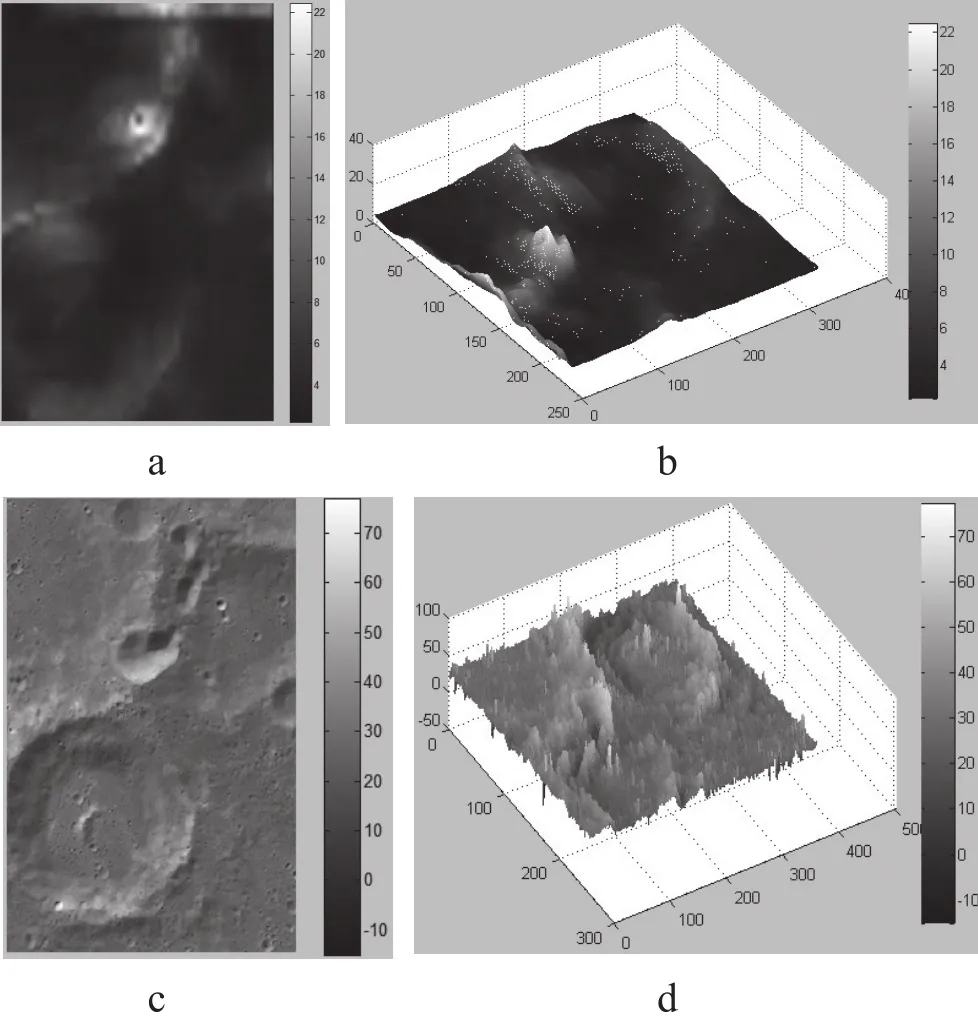
图6 用本文方法和最小化SFS恢复的图像深度图。
从精度表可以看出,本文算法重建的三维模型高度标准差要优于传统的最小化SFS方法,其最大高度和最小高度差均小于最小化方法,且高度误差在一个较小的范围内变动,说明其重建表面更为稳定平滑,不存在剧烈跳变噪声。本文提出的方法对全幅影像进行三维表面重建,结果相较于传统方法精度更高。
3 结 语
在非特征边缘及缺乏纹理区域,特征点提取的数量较少,立体匹配会存在较大误差。而SFS利用单幅影像上亮度变化与表面形状变化之间的关系来反演表面形状,可基于单张影像直接进行三维重建。SFS理论需要添加一系列边界条件或控制点信息来保证其解的稳定性。将两种方法结合起来,可以很好地发挥SFS方法和立体视觉各自的优势,并互相补充不足,即使在光滑和纹理缺乏的区域也能得到较好的重建结果,得到更为稳定和精确的重建表面。本文的方法基于朗伯体表面假设,而如何建立更为精确的物理模型,准确描述地表法向量、地表不同反射率以及光源方向之间的关系,是影响该方法重建精度的一个重要问题,值得深入探讨和研究。

