基于ICEEMD-PE的脑血氧降噪方法研究
吴 凯 张 欢 刘 燕 戴亚康
(1.中国科学院大学 北京 101407)(2.中国科学院苏州生物医学工程技术研究所 苏州 215163)(3.南京理工大学电子工程与光电技术学院 南京 210094)
1 引言
人体脑血氧在临床治疗和诊断中起着重要的作用,例如脑外伤[1]和心脑血管疾病的治疗和检测等。脑血氧信号的检测是通过组织中血红蛋白等对近红外光的吸收,得到光密度的变化情况,再结合修正的朗伯-比尔定律计算得出组织内的氧合血红蛋白(oxygenated hemoglobin,oxy-Hb)和脱氧血红蛋白(deoxy-genated hemoglobin,deoxy-Hb)的浓度变化即人体脑血氧信号[2]。
然而,由于采集的脑血氧信号十分微弱,因此在测量时非常容易受到外界的干扰。这些干扰主要有被测对象运动和呼吸等活动而产生的低频干扰,基线漂移[3];采样过程中仪器或环境的磁场等产生的高频干扰[4],高频噪声。以上的干扰严重影响了信号的精确度,致使结果出现较大的误差。
目前针对血氧的去噪方法主要有最小均方误差(LMS)自适应算法,小波变换和经验模态分解(Empirical Mode Decomposition,EMD)[5]等。其中,LMS自适应算法虽然结构较为简单、计算量小且稳定性能好,但固定步长导致跟踪速率、收敛速率和失调噪声之间相互矛盾[6];小波变换可以对空间和频率进行多尺度细分分析,但要事先选定小波基函数、分解层次等[7];EMD则根据信号本身特点,自适应产生基函数将信号分解成一系列本征模态函数(Intrinsic Mode Function,IMF)[8],解决了小波变换对基函数的依赖问题,但依然存在模态混叠现象[9]。针对EMD的不足,Huang提出的总体经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[10]在信号中添加不同的高斯白噪声,在多次EMD分解后将得到IMF进行平均,有效解决了问题。然而,在实验有限次的情况下,添加的高斯白噪声没有完全抵消,重构分量中存在残留噪声[11]。因此,提出了一种基于EEMD的具有自适应白噪声的完全总体经验模态分解(Complete Ensemble Em⁃pirical Mode Decomposition with Adaptive Noise,CEEMDAN)[12]将残留噪声基本去除,但在分解的前期仍然存在着虚假模态问题,使得信号出现延迟现象,影响了信号的重构。
为了解决上述问题,一种新的方法——改进的总体完备经验模态分解(Improved complete ensem⁃ble EMD,ICEEMD)[13]被提出,利用各模态当前的局部均值重新定义真实模态,成功解决了CEEM⁃DAN面临的问题。然而,无法对ICEEMD在分解信号得到多个IMF进一步判断,往往根据经验进行信号重构,存在极大的误差。因此,本文引入一种衡量空间复杂度的算法,排列熵。
排列熵(Permutation Entropy,PE)[14]对时间非常敏感,可获得较高的分表率,而且计算方法简单,抗噪声能力强。因此,本文将ICEEMD和排列熵相结合的方法去除信号中存在的基线漂移和高频噪声。
2 算法原理与分析
2.1 ICEEMD算法
记原始信号为 x(n),算子 Ek(.)和 M(.),Ek(.)表示EMD分解得到的第k个模态;M(.)则满足M(x(n))=x(n)-E1(x(n)),ICEEMD 分解得到的得到的模态分量个数。其分解步骤如下:
1)对x(n)添加高斯白噪声生成新的信号,wi表示第i组添加的高斯白噪声,如下式:
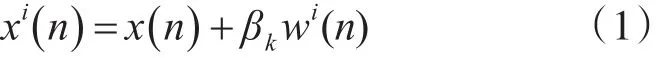
其中,i=1,2,…,I,βk使得每个分解阶段选择合适的信噪比。

重复上述步骤便可得到原始信号所有的模态分量。
2.2 排列熵算法
将ICEEMD分解得到的模态分量IMFk(t),k=1,2…,K表示模态分量个数,t=1,2,…,n,进行空间重构,得到矩阵如下:
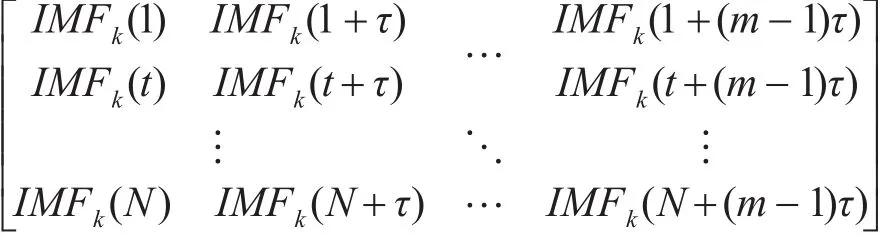
其中N=n-(m-1)τ,m为嵌入维数,τ为延迟时间。矩阵中每行都可以看成是一个重构分量,根据数值大小,将其按升序进行排序,得到新的重构分量,如下式表示:
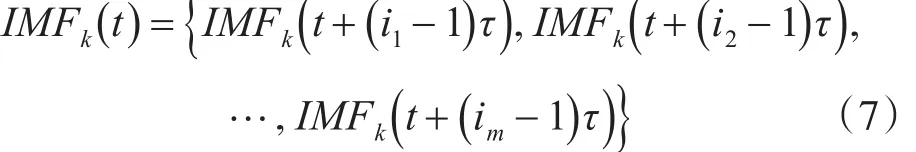
其中,每个元素满足如下关系:
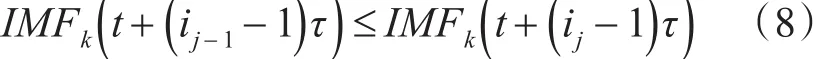
式中j=2,3,…,m,因此 IMFk重构所组成的矩阵中,每行都含有一组符号序列S(q)=(i1。i2。…。im),式中q=1,2,…,N,且N ≤m!种不同排列方式,不同的序列出现的概率为P,得到IMFk分量的排列熵为
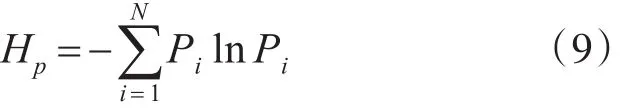
为了方便,将Hp进行归一化处理,即:
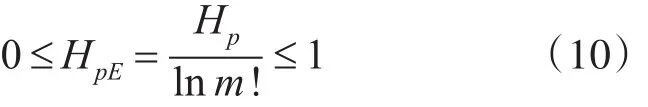
根据上式计算可得出各IMF分量的排列熵,HpE越大表明该分量越随机;反之,则越规则。选取阈值剔除高频噪声和基线漂移,得到有用分量IMFm~IMFn,将其重构产生去噪后的信号x',表达式为

2.3 性能对比实验
为了验证算法的优越性,在这里设计了一个对比实验。设原始信号S分别由信号S1、S2所示组成,如下式:
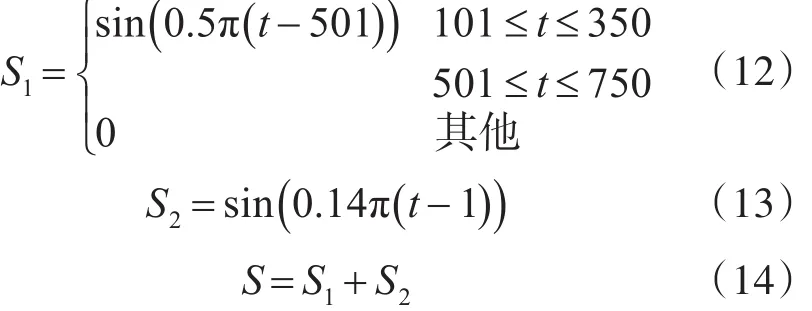
将原始信号分别进行EMD分解、EEMD分解、CEEMDAN分解和ICEEMD分解,然后观察其IMF分量。
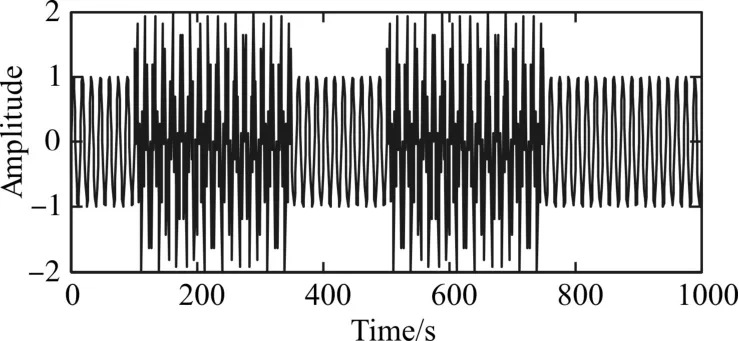
图1 原始信号S
模拟信号的分解实验结果如图2所示,从图(a)可以看出,EMD分解后得到的IMF分量中IMF1、IMF2和IMF3明显是由多种不同时间尺度的信号组成,即存在模态混跌现象;从图(b)可以看出,EEMD分解后的IMF分量可以很好地将两种不同频率、不同幅值的信号分解出来,分别为IMF1和IMF2,但是存在IMF3~IMF9的噪声残留;从图(c)可以看出,CEEMDAN分解后的IMF分量IMF1和IMF3之间明显存在虚假模态IMF2;从图(d)可以看出,ICEEMD可以将两个不同的模拟信号很完美地分解出来。因此,ICEEMD可以将非线性非平稳的时频信号很好的分解为一系列不同时间尺度的IMF分量。
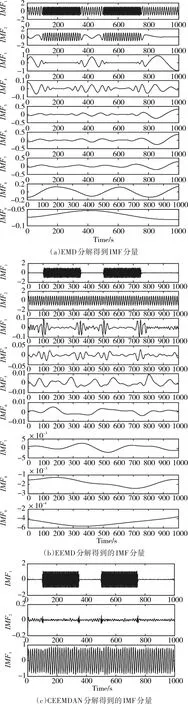
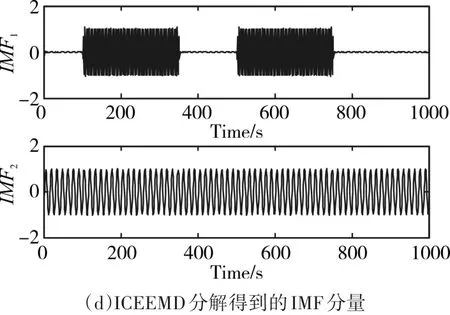
图2 分解得到IMF分量
3 实验与结果
3.1 实验步骤
利用自制的设备对脑血氧信号进行采样,即氧合血红蛋白和脱氧血红蛋白的浓度变化信号,之后按本文提出的算法进行处理,验证方法的效果。图3为设备的电路结构框图。200组的高斯白噪声,标准差为0.2,最大的迭代次数为500次。
3)将通过ICEEMD分解而产生的两组IMF分量引入排列熵计算,本文选择的m=7,τ=1。
4)多次重复实验,统计出实验结果。根据排列熵的结算结果,选择合适的阈值,进行信号重构。
3.2 实验结果
根据上述的实验步骤,得到oxy-Hb和de⁃oxy-Hb的原始浓度变化信息和经过ICEEMD分解后的IMF分量信息,如图4所示;将得到的IMF分量引入PE计算,得到的结果如表1所示。
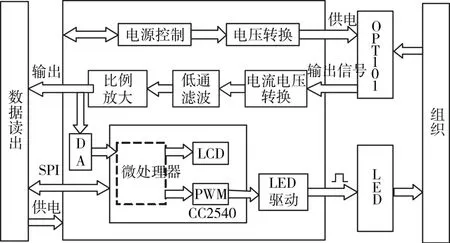
图3 脑血氧检测电路结构图
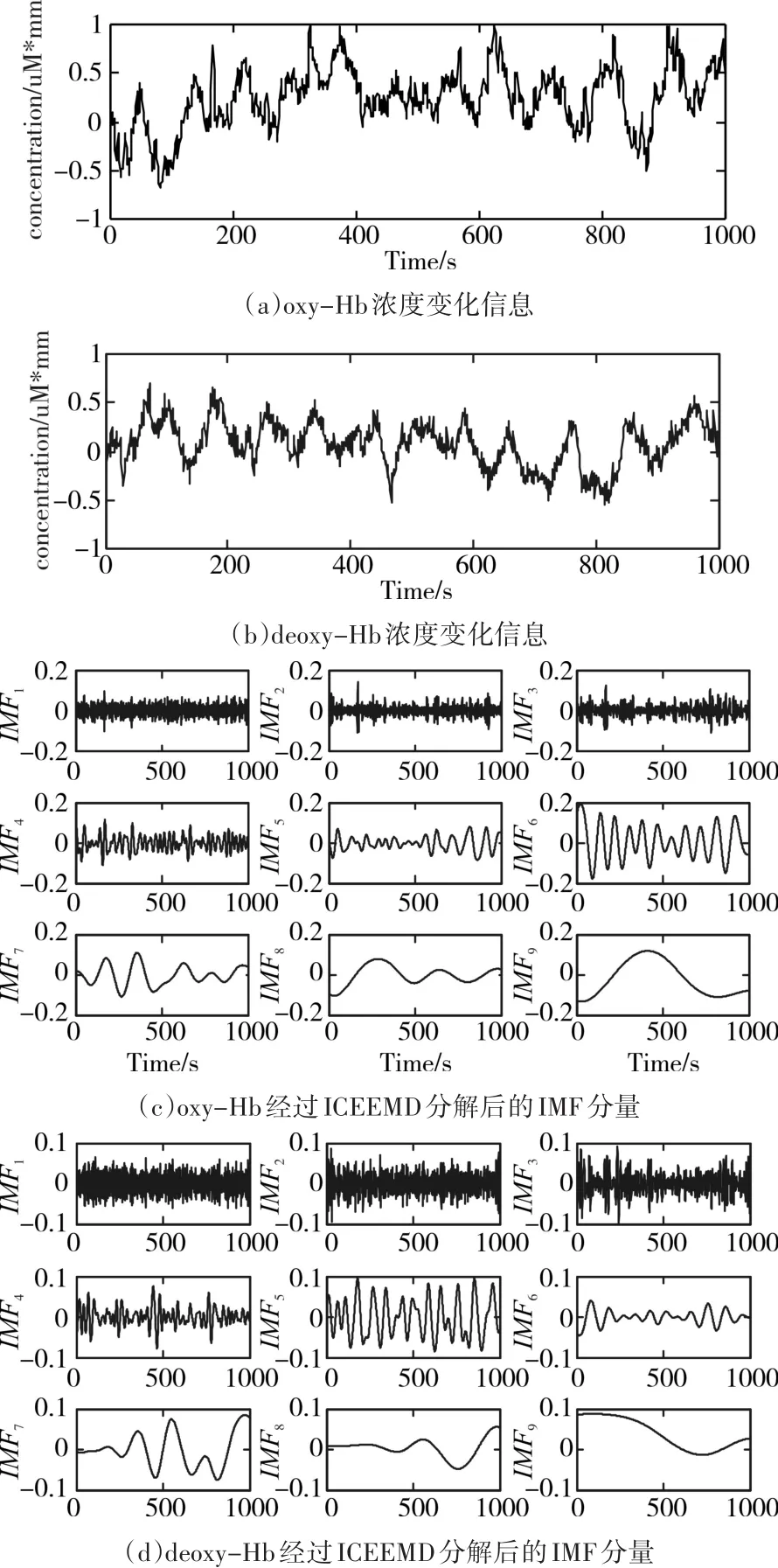
图4 血红蛋白浓度变化的原始信号和经过ICEEMD分解后得到的IMF分量
电路中,微处理器选择美国德州仪器生产的CC250芯片,光源LED选择EPITEX公司生产的SMT 660/910双波长LED,检测器采用光敏管OPT101芯片。首先,微处理器输出PWM波控制不同波长的LED轮流发光射入大脑,以距离光源3cm的光敏管将出射光信号转化为电信号;然后,经过电流电压转换,低通滤波,比例放大,AD转换等一系列处理后,由CC2540通过USB和BLE4.0两种方式传入上位机,并对数据进行处理。具体的处理步骤如下:
1)利用近红外光谱技术,以10Hz的采样频率采集脑部入射光和出射光的光密度信息,将结果做集成平均运算。然后,利用修正的朗伯比尔定律计算出oxy-Hb和deoxy-Hb的浓度变化信息。
2)分别对oxy-Hb和deoxy-Hb进行ICEEMD分解,得到一系列IMF分量。其中,加入试验次数为

表1 ICEEMD分解得到IMF分量的排列熵
3.3 结果分析
根据上述实验进行多次实验,经过统计计算后,这里将PE值超过0.5的IMF分量视为高频噪声;PE值低于0.2的IMF分量视为低频的基线漂移。所以,选在该范围内的IMF分量进行信号重构,得到降噪后的信号。
图5、6分别为oxy-Hb和deoxy-Hb的原始浓度变化信号及其对应的频谱信息和降噪之后的浓度变化信号和频谱信息的对比。从两张图的(a)和(c)可以直观地看出去噪后的信号光滑度更好,且从(b)和(d)中可以看出,高于10Hz的高频噪声被有效地抑制了。
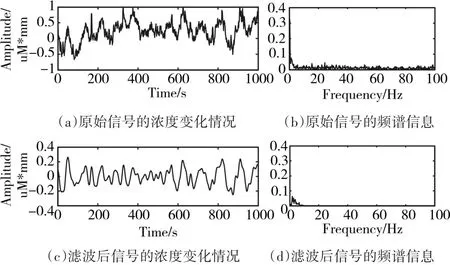
图5 oxy-Hb的浓度变化情况
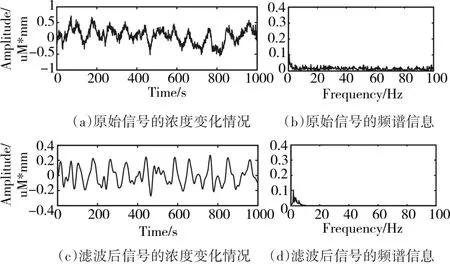
图6 deoxy-Hb的浓度变化情况
基线漂移主要是影响信号的稳定性,但是在人体的血液中,血红蛋白的总体浓度趋于稳定[15~16]。分别计算出去噪前后的血红蛋白的变化量,结果如图7所示。从图中可以看出,去噪之后的血红蛋白浓度变化更为稳定,很好地抑制了基线漂移问题。
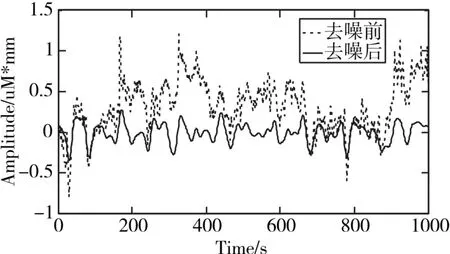
图7 降噪前与降噪后的血红蛋白浓度变化对比
4 结语
本文提出了一种ICEEMD和排列熵相结合的脑血氧降噪方法,利用了ICEEMD根据信号自身从而自适应的将信号分解为一系列不同尺度的模态分量。该方法与EMD相比,解决了模态混叠问题;与EEMD相比,解决了残余噪声问题;与CEEM⁃DAN相比,则解决了虚假模态问题。此外,利用排列熵判断IMF分量的时间复杂度,为信号的重构提供了依据,进一步提高了重构信号的精确度。通过实验证明,本文提出的方法可以有效抑制脑血氧信号中存在的基线漂移和高频噪声问题。

