考虑零控拦截的中制导最优弹道修正
周觐, 雷虎民
(空军工程大学 防空反导学院, 陕西 西安 710051)
0 引言
临近空间高超声速武器是以高超声速飞行器为载体或直接作为武器本体使用,长时间在临近空间飞行的武器,具有作战空间大、飞行速度快、突防能力强以及毁伤力大等特点,能突破目前几乎所有的防御体系,对我国空天防御作战提出了极大的挑战,开展临近空间防御作战研究已迫在眉睫[1-2]。现有武器系统在应对临近空间高超声速武器作战环境下面临的主要挑战可归结为:1)临近空间高超声速武器具有较高的飞行速度,导致防御方拦截窗口较小,可拦截条件转瞬即逝[3]。尤其在拦截末段,末制导时间很短,供拦截弹的调整修正时间有限,因此拦截弹在中制导和末制导交接班时必须处于较好的拦截态势[4],否则难以成功命中目标;2)现有武器系统的中制导段大多采用比例导引[5]或弹道成型等制导律[6],对于最优弹道设计以及最优化的弹道修正等问题考虑较少。在临近空间防御作战环境下,由于非合作目标的机动及目标周围等离子鞘套干扰等带来的影响,目标实际飞行状态很难精确获得,对于目标的预测运动状态也需进行持续更新[7],这就要求拦截弹在实际飞行作战过程中适时修正自身弹道,满足目标信息更新后的最佳拦截条件。
综合考虑以上两点的相关文献研究较少。作为中制导的终端条件以及末制导的初始条件,中制导和末制导交接班时拦截弹的状态至关重要[3]。为有效设定中制导和末制导的最佳交接条件,郑立伟等[8]针对大气层外中段拦截问题,推导得到了一种考虑飞行器重力差影响的零控脱靶量关系式,宋剑爽等[9]提出了广义零控拦截流型的概念,张浩强等[4]研究了考虑临近空间零控交班条件的指令修正中制导设计,得出了连接中制导和末制导阶段的有效零控拦截交班区域。这些研究为中制导和末制导交接班时刻的拦截弹状态约束建立提供了有力借鉴。中制导段的弹道修正思路主要分为两类[10-12]:1)利用高效的优化算法将当前状态与约束状态作为边值条件,对弹道进行重新优化,如伪谱法[13]、粒子群方法[14]等。由于需要在线求解最优化问题,这种思路的主要缺点是对算法的求解精度以及求解效率提出了较高要求;2)将改变后的约束条件作为基准状态的扰动,利用线性化方法求解所需的控制量补偿量,如文献[15-18]研究并提出的模型静态预测规划算法。通过对系统的状态偏差方程进行1阶泰勒级数展开,将终端的状态约束偏差表示成为偏微分方程的连乘积形式,然后采用迭代优化的方法对控制量进行修正。但是模型静态预测规划算法的迭代次数及迭代精度都未能得到有效理论证明,因此其在线适用能力无法得到保证。Pontani等[10-12]应用邻域最优控制理论研究了月球飞行器的轨道修正问题,设计了一种邻域最优化制导算法。该算法将终端状态修正量作为反馈代入到基准弹道的哈密尔顿方程及状态方程,通过一次性求解即可得到基准控制量的最优补偿量。以上思路充分利用了基准弹道信息,避免了对于控制量的再次大范围寻优,因而一般时效性较高。
本文针对临近空间防御作战中面临的交班条件和弹道修正两方面挑战,提出了一种最优化的中制导弹道修正算法。
1 中制导和末制导交接班的零控拦截条件分析
1.1 末制导段拦截弹和目标运动分析
为叙述方便,首先引入如下假设条件:
假设1拦截弹的弹上导引头最大作用距离为Rmax,忽略中制导和末制导交接班中的导引头开机搜索与目标截获过程,认为只要拦截弹与目标之间的距离小于Rmax,导引头即可成功截获目标,中制导和末制导交接班结束并顺利转入末制导阶段。
假设2考虑临近空间目标的典型特点,认为在中制导和末制导交接班以及末制导阶段,目标速度大于拦截弹速度,即目标与拦截弹的速度比Δ=‖vT‖/‖vM‖>1成立。
假设3考虑目标和拦截弹较大的相对运动速度,认为在末制导阶段目标不机动,拦截弹的过载指令只改变速度方向。
末制导阶段垂直平面内拦截弹和目标的相对运动关系如图1所示。
图1中:OXZ为惯性参考坐标系;拦截弹M和目标T之间的连线称为视线(LOS);R为M和T之间的距离;vM、vT和aM、aT分别为速度矢量和加速度矢量;θ为相应速度矢量与水平面之间的夹角,即弹道倾角;qLOS为LOS与水平面之间的夹角,即LOS角;γ为拦截弹速度矢量与LOS之间的夹角,η为目标速度矢量与LOS之间的夹角,γ和η均为速度前置角。由图1可得到以下运动方程:
(1)
(2)
(3)
γ=θM-qLOS,
(4)
(5)
(6)
(7)
η=qLOS-θT,
(8)
(9)
(10)
式中:(XM,ZM)和(XT,ZT)分别为拦截弹和目标在OXZ坐标系中的位置。
结合假设3可得到aT=0,则(7)式可进一步简化为
(11)
1.2 中制导和末制导交接班零控拦截条件分析
定理1假设目标不机动,目标和拦截弹的速度比Δ=‖vT‖/‖vM‖>1,那么在中制导和末制导交接班过程中拦截弹和目标存在零控拦截条件,并且此条件由目标和拦截弹的速度比及二者的速度矢量分别与LOS之间的夹角,即二者各自的速度前置角,唯一确定。
证明为便于零控拦截条件的分析与证明,对图 1作进一步变形,以目标速度矢量的终点O′作为圆心,以拦截弹速度矢量vM的模值‖vM‖为半径作圆,与弹目LOS分别相交于A点和B点,如图2所示。如果拦截弹速度矢量ME满足ME=BO′(或ME=AO′,证明过程相同),那么拦截弹和目标即满足零控拦截条件。
通过圆心O′做垂线与LOS相交于G点,那么在△AO′B可得
‖O′G‖=‖vM‖sinγ=‖vT‖sinη,
(12)
sinγ=Δsinη.
(13)
将(12)式代入(10)式可得
(14)
由(13)式进一步推导可得
(15)
将(15)式代入(9)式并进行化简可得
(16)
根据假设2中目标和拦截弹的速度比Δ=‖vT‖/‖vM‖>1,由(16)式可知:
(17)
综合(14)式及(17)式可得,如果目标不机动,且目标和拦截弹的速度比Δ=‖vT‖/‖vM‖>1,那么拦截弹无需施加额外的制导指令即可成功拦截目标,即拦截弹和目标满足零控拦截条件,此条件由(13)式唯一确定。
进一步观察图2可发现,零控拦截边界条件为LOS与拦截弹速度矢量圆相切的情形,假设切点分别为C点和D点,此时有
γ=±π/2 rad.
(18)
将(18)式代入(13)式可得
ηmax=arcsin(1/Δ),
(19)
从而可得目标的速度前置角η取值范围为
-ηmax≤η≤ηmax.
(20)


2 中制导最优弹道修正算法
2.1 中制导段拦截弹运动模型
拦截弹在拦截高速目标作战中,通常选择高抛再入拦截弹道,即在有动力阶段快速爬升穿过底层稠密大气层,而后在无动力阶段从高空再入打击[19]。这样既可有效节省能量,又有利于弹上导引头更好地探测及捕获目标[3]。由于有动力阶段的弹道设计目标主要是合适的关机点高度及关机点速度,而无动力阶段主要考虑目标机动情况下的弹道优化及修正,所以本文选择无动力阶段为主要研究对象,拦截弹数学模型[20]可表示为
(21)
(22)
(23)
(24)
(25)
(26)
式中:(x,y,z)为拦截弹在地面坐标系中的位置;v为拦截弹速度;ψ为弹道偏角;re为地球半径;g为重力加速度;m为拦截弹质量;q为动压;S为拦截弹参考面积;β为侧滑角;CL和CD分别为升力系数和阻力系数。
为保证拦截弹的直接碰撞杀伤效果,一般以中制导结束时刻的速度最大作为优化指标:
J=φ(x(tf),tf)=-vf,
(27)
式中:tf为中制导结束时间;vf为中制导结束时刻的速度。
结合第1节分析可知,中制导段应确保在中末制导交接班时刻拦截弹处于零控拦截条件,包括中制导终端位置约束及角度约束条件,即
(28)
式中:ψf为中制导结束时刻的弹道偏角;下标d为相应状态量的期望值。
过程约束主要考虑拦截弹的热流密度Q不超过材料所能承受的最大值Qmax=2.5×105W/m2,即
(29)
式中:qa0、qa1、qa2、qa3为热流密度系数;ρ为空气密度:α为拦截弹攻角。
参考文献[20]中对控制量的限制,同时结合拦截弹实际特点,本文中控制量约束设定为
(30)
2.2 中制导最优弹道修正

(31)
(32)

(33)
(34)
ψf(x(tf))=0,
(35)
在拦截弹中制导段,由于目标机动或对于目标预测信息的更新,中制导和末制导交接班时刻拦截弹和目标的运动状态将发生改变,从而不满足预先设计的零控拦截条件。这时就需根据目标信息对中制导和末制导交接班时刻拦截弹的状态约束进行调整。记预先设计的基准约束条件为ψ*,根据目标预测信息修正后的终端约束条件为ψ,则终端约束的修正量为δψf=ψ-ψ*. 中制导段的最优弹道修正可以表述为:当中制导终端约束条件发生改变时,通过对原有的基准控制量u*进行一定的补偿δu得到修正控制量u=δu+u*,从而对拦截弹的基准状态量x*进行调整δx=x-x*,使x满足改变后的终端约束条件ψ,并且在一定程度上保持性能指标J的最优性。
中制导段的最优弹道修正可以看作基准弹道状态上的扰动,对于最优控制条件(33)式及横截条件进行进一步微分可得
(36)
(37)
(38)
式中:dν为终端乘子的调整量,dν=ν-ν*. 如果∂2H/∂u2非奇异,那么根据(36)式可得到控制量的修正量δu表达式为
(39)
对状态方程(31)式及协态方程(32)式在基准弹道附近进行线性化,并将(39)式代入可得
(40)
(41)
式中:
(42)
(43)
(44)
观察(37)式和(38)式可发现,偏微分后中制导和末制导交接班时刻协态的修正量δλ(tf)和终端约束的修正量δψf表示成为了关于状态修正量δx和终端乘子修正量dν的线性表达式:
δλ(tf)=[S(t)δx(t)+R(t)dν]f,
(45)
δψf=[RT(t)δx(t)+Q(t)dν]f,
(46)
式中:S(t)、R(t)、Q(t)为引入的时变矩阵,且满足[10-12]:
(47)
(48)
Qf=0,
(49)
(50)
(51)
(52)
以时变矩阵S(t)、R(t)、Q(t)的终端条件(47)式~(49)式为初值,以(50)式~(52)式为系统方程进行逆向积分,可得到dν在初始时刻的表达式为
(53)
将(53)式代入(45)式,可得到初始时刻的协态变量偏差量
δλ0=[(S-RQ-1RT)δx+RQ-1δψf]0.
(54)
通过观察(54)式可看出,协态量的偏差量δλ表示成初始时刻状态偏差量δx及终端约束偏差量δψf的表达式,而δx和δψf都可通过拦截弹上的敏感测量装置或地面探测设备解算得到,从而确保了最优弹道修正算法的可实现性。由于最优弹道修正算法对基准弹道所满足的1阶最优性条件公式(31)式~(35)式进行2阶变分得到,具有2阶最优性[10]。利用(39)式进行一次求解即可得到最优修正量δu,避免了伪谱法中对控制量的再次大范围寻优求解TPBVP以及模型静态预测规划中对控制量的迭代更新,所以具有更高的求解精度以及求解效率。
综上所述,考虑零控拦截的中制导最优弹道修正算法步骤如下:
步骤1根据预警系统得到的目标运动信息以及拦截弹中制导和末制导交接班时刻预设运动状态,结合(13)式判断是否满足零控拦截条件。如果满足,则继续保持对目标跟踪预测,重复步骤1;如果不满足,则进入步骤2.
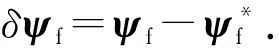
步骤3利用(47)式~(49)式计算矩阵Sf、Rf和Qf,将其作为初始值代入到状态方程(50)式~(52)式进行逆向积分至初始时刻t0得到S0、R0和Q0.
步骤4将S0、R0、Q0、δx0和δψf代入(53)式和(54)式,得到dν和δλ0的值。
步骤5将初始时刻状态量的偏差量δx0和协态量的偏差量δλ0代入(40)式和(41)式进行积分,得到δx(t)和δλ(t)后代入(39)式,计算控制量的补偿量δu(t).
步骤6将控制量的补偿量δu(t)与基准控制量相加得到更新的控制量u(t)=δu(t)+u*(t)并以此为控制指令代入到拦截弹状态方程(21)式~(26)式,得到更新后的中制导和末制导交接班时刻拦截弹状态ψ=δψf+ψ*,完成考虑零控拦截的中制导最优弹道修正,返回步骤1.
3 仿真结果与分析
为验证本文所设计方法的有效性,开展两种情形的仿真,设定仿真中拦截弹导引头最大作用距离Rmax=100 km,利用伪谱法[21]获得仿真的基准弹道,中制导过程中目标在交接班时刻的状态信息依靠远程预警系统或拦截弹的火控雷达预测得到。仿真平台相关参数为:Intel Core i7 3.4 GHz处理器,4 G内存,Windows XP x86操作系统,伪谱法采用MATLAB程序包GPOPS,本文方法和模型静态预测规划方法采用MATLAB R2014a平台编写。
3.1 情形1
仿真中想定的拦截弹和目标有关参数设置如表1所示。
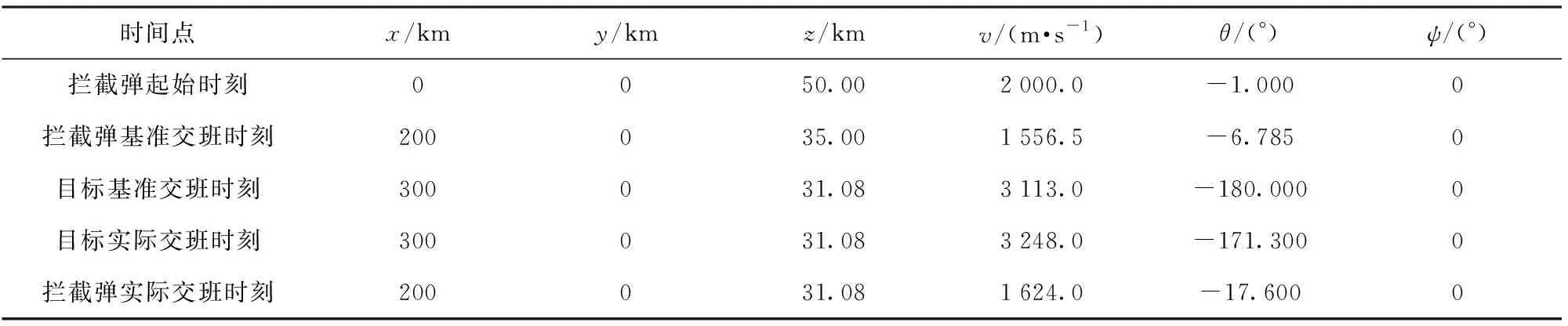
表1 情形1参数设置
此仿真情形设计的目的是检验本文算法对中制导弹道修正的有效性。由表1可知,在非精确信息支援条件下,目标在交接班时刻预测的飞行弹道倾角为-180°,此时设计的拦截弹基准交接班时刻高度为35 km,弹道倾角为-6.785°,目标和拦截弹的速度比为Δ=3 113.0/1 556.5=2,通过(10)式可计算验证,基准弹道的最初设计满足零控拦截条件。随着拦截过程的进行及目标探测精度的提高,对中制导和末制导交接班时刻目标的预测状态也将进行更新,更新后的目标实际交接班时刻弹道倾角为-171.3°,速度为3 248 m/s,则此时要求拦截弹在中制导阶段进行最优弹道修正,满足目标状态更新后的零控拦截条件。为进一步体现本文算法的优越性,将本文算法得到的结果与参考文献[4]模型静态预测规划方法及伪谱法[21]重新优化得到的结果进行比较,如图3~图9所示。
图3所示为情形1拦截弹弹道曲线。
由图3可见,本文方法和伪谱法得到的修正弹道比较平滑,参考文献[4]得到的修正弹道出现了一定跳跃。
图4和图5所示为情形1弹道倾角曲线和弹道偏角曲线。
由图4和图5可知,虽然3种方法都能将拦截弹的弹道倾角调整到约束状态-17°附近,但本文方法和伪谱法得到的弹道倾角变化曲线要优于参考文献[4]得到的结果。由于参考文献[4]得到的弹道倾角在倾角0°处发生了2次穿越,从而造成了图3中拦截弹弹道的2次跳跃。由于目标在侧向y轴方向未发生机动,所以3种方法得到的修正弹道都能够保持弹道偏角为0°,从而确保y轴方向位移为0 km.
图6所示为情形1速度曲线。
由图6可见,本文方法和伪谱法对于性能指标,即中制导和末制导交接班时刻速度大小能够很好地保持其最优性。
图7和图8所示为拦截弹攻角曲线和侧滑角曲线。
由图7和图8可见,本文方法和伪谱法得到的控制量整体变化幅度比较小,优于参考文献[4]方法。
图9所示为情形1拦截弹热流密度变化曲线。
由图9可知:参考文献[4]方法得到的热流密度峰值出现在55 s处,为198.5 kW/m2;本文方法和伪谱法得到的热流密度峰值出现在终端时刻,分别为170.1 kW/m2和195.2 kW/m2;3种方法得到的热流密度都没有超过最大热流密度限制,从而确保了飞行安全性。
3种方法得到的交接班时刻拦截弹状态及时间消耗对比如表2所示。
由表2可知,3种方法都能将中制导和末制导交接班时刻拦截弹的弹道高度修正到目标高度附近,从而确保此时LOS角qLOS≈0°,在x轴方向基本满足弹上导引头最大探测距离约束。本文算法得到的最终速度为1 624 m/s,伪谱法得到的最终速度为1 584 m/s,相对表1中基准交接班时刻拦截弹速度1 556.5 m/s变化不大。但参考文献[4]方法得到的速度为1 236 m/s,相比于基准速度减小了320.5 m/s,原因在于参考文献[4]方法是一种次优化方法,并不能保证其求解指标的最优性[17]。通过计算可进一步发现,本文方法和伪谱法得到的目标和拦截弹速度比Δ≈2,本文方法得到的修正后速度前置角γ=16.1°,参考文献[4]方法及伪谱法得到的修正后速度前置角γ=17.7°,目标的速度前置角为η=8.7°,根据(10)式可得本文方法和伪谱法的修正弹道基本满足了零控拦截条件。参考文献[4]方法中目标和拦截弹的速度比为Δ=2.67,并不满足零控拦截条件,原因在于零控拦截条件与目标和拦截弹的速度比及二者的速度前置角决定,参考文献[4]方法虽能通过调整弹道及拦截弹角使其满足速度前置角的约束,但对于速度性能指标的影响不可预知,从而影响了目标和拦截弹的速度比。

表2 情形1交班时刻拦截弹状态与消耗时间对比
3.2 情形2
情形1验证了本文算法的最优性和有效性,在仿真情形2中,通过多次更新中制导和末制导交接班时刻目标预测运动状态,来检验本文算法的多次弹道修正能力。作战想定为:在开始时刻,保持情形1的目标预测运动状态,拦截弹按照第1次修正后的弹道进行飞行。在第40 s时刻,对目标的预测状态进行更新,其运行高度保持不变,侧向位移为3 km,预测弹道倾角更新为-168.4°,如表3所示情形2参数设置。

表3 情形2参数设置
情形2的仿真结果如图10~图16所示,不同方法得到的交接班时刻拦截弹状态与消耗时间如表4所示。
由图10可见,修正后的弹道比较平滑。由表4可见,修正弹道基本都能达到中制导和末制导交接班约束的位置,其中伪谱法能够很好地满足终端约束,而参考文献[4]方法与终端约束差别最大。原因在于伪谱法以当前时刻状态及终端状态为约束对弹道进行了再次优化,优化方法的精度较高。由于对当前时刻的状态量偏差dx定为0,但实际情况下在第2次弹道修正中与基准弹道相比状态已产生了调整,所以造成参考文献[4]方法的假设条件不能很好满足,得到的结果精度也会下降。由图11和图12可知,第1次修正和第2次修正后的拦截弹弹道倾角和弹道偏角都收敛到了不同的终端约束状态。在40 s时刻第2次修正中,3种方法都能对弹道进行有效调整,修正后的弹道倾角和偏角基本能收敛到-23°和0°附近。本文方法得到的弹道倾角为-21.7°,偏角为1.1°;参考文献[4]方法得到的弹道倾角为-22.4°,偏角为0.2°;伪谱法得到的弹道倾角为-23.7°,偏角为0°. 由图13可见,参考文献[4]方法对速度影响较大,最后速度为1 183 m/s,本文方法得到的速度为1 507 m/s,伪谱法得到的速度为1 327 m/s. 结合(13)式可得到,本文方法与零控拦截条件的偏差为-0.065,伪谱法偏差为-0.091,参考文献[4]方法偏差为-0.172,本文方法得到的修正结果要优于其他2种方法。由图14和图15可见,伪谱法控制量在最后时刻出现了震荡,参考文献[4]方法和本文方法得到的控制量曲线相对平滑。

表4 情形2交接班时刻状态与消耗时间对比
由图16可见,热流密度维持在约束范围之内。从表4消耗时间对比可知,本文方法解算效率要高于其他2种方法,同时和情形1的耗时情况相比可知,由于中制导段剩余飞行时间的缩短,需解算的变量更少,情形2耗时更小。
4 结论
本文重点研究了考虑零控拦截的中制导最优弹道修正,通过分析拦截弹和目标相对运动过程中存在的零控拦截条件,建立了中制导和末制导交接班时刻拦截弹需要满足的位置约束以及零控拦截条件约束,利用最优化理论推导设计了中制导段弹道的最优修正算法。得到结论如下:
1)在拦截弹和目标的相对运动过程中存在零控拦截条件,此条件由目标和拦截弹的速度比及二者速度矢量与LOS之间的夹角,即速度前置角,唯一确定。
2)以拦截弹弹上导引头的最大作用距离作为中制导和末制导交接班时刻的拦截弹位置约束,以零控拦截条件作为拦截弹弹道角度约束,能够得到最佳的中制导和末制导交接班态势。
3)当中制导段对目标的预测状态不满足零控拦截条件时,需要对拦截弹的弹道进行修正。在确保性能指标满足一定的最优性同时,调整中制导和末制导交接班时刻拦截弹状态,确保满足零控拦截条件。
4)本文设计的最优弹道修正算法相比参考文献[4]中模型静态预测规划方法及伪谱法,具有较高的精度和较快的求解效率,适于在线弹道修正指令解算。

