行进间火炮指向稳定跟踪系统建模与控制
李伟, 姜俊峰, 任海波, 张光辉
(1.西北机电工程研究所, 陕西 西安 712099;2.浙江大学 浙江省先进制造技术重点实验室, 浙江 杭州 310027)
0 引言
自行火炮具备行进间稳定瞄准跟踪射击能力是新军事斗争的迫切需求。火炮在稳定系统控制下,与坦克或突击炮的火炮控制系统功能相似,不但要克服载体姿态变化对火炮指向的扰动,而且需具有足够的带宽跟随火力控制解算的射击诸元,但坦克属于直瞄武器,其射角低于20°,方位功率只有几千瓦。类似设备如光电视线跟踪因其负载小、响应快,稳定系统不局限于某种载体平台,且在其高低角全范围都能达到较高精度[1-5]。自行火炮射角约为85°,随着射角增大,方位稳定系统所需功率急剧增大[6],才能克服载体姿态扰动。同时,火炮转动惯量大、质量大,并存在较大不平衡力矩、传动齿隙和刚度等因素对火炮稳定系统产生较大影响。
自行高炮行进间射击时,火炮既受到射击力作用,同时又受到行驶中由于地面不平度而造成的路面激励作用及发动机振动,尤其路面不平度导致车体颠簸,造成炮口振动是影响精度的主要因素。因此,自行高炮在行进间射击时必须有合理的车速及较好的路况条件[7]需求,极大地限制了其机动性和作战能力。传统自行高炮采用解算式稳定,由火力控制系统随时修正车体姿态造成的射击偏差,首先解算以火炮为原点的水平坐标系下射击诸元,再转换至载体坐标系下的射击诸元,作为火炮随动跟踪指令,由等效闭环的随动在载体坐标系内稳定火炮指向。这种方式造成火炮稳定响应滞后,难以适应车体姿态快速变化。舰炮稳定与自行高炮类似,对大吨位舰船,由于舰船摇摆周期较长,姿态扰动能量主要集中在低频段,相对较易实现,对小吨位舰艇仍面临自行高炮所面临的难题。
随着捷联惯性导航系统(SINS)技术的进步,其航姿测量精度、长期稳定性和抗冲击能力等性能大幅提高,且成本较低。将SINS安装在自行火炮身管上直接测量火炮在大地坐标系的指向进行瞄准已是现代自行火炮的成熟技术,火力控制弹道解算可给出大地坐标系下的射击诸元[8]。自行火炮随动系统将SINS的航向和俯仰角作为其角度反馈,实现了火炮在大地坐标系下的全闭环直接控制,提高了火炮瞄准精度。传统方式控制下,因为火炮调转运动与SINS测量坐标不统一,造成高低和方位随动控制系统存在耦合,影响瞄准的快速性。对于只能驻停间发射的自行火炮可灵活采用四元数、欧拉角法等坐标变换或串级控制来解决。而对于行进间瞄准射击的自行火炮需采用既能抑制载体扰动,又能很好解决控制耦合下的稳定跟踪瞄准问题的新方法。
在火炮指向的动力学分析、控制方法和策略等研究中,系统建模技术具有重要作用。田建辉[9]对火炮身管指向定位和跟踪控制方法进行了理论分析,但动力学建模上没有考虑载体运动导致的载体、炮塔与火炮控制三者轴间的耦合力矩,忽略了各转动部件的重心偏移,控制上忽略了执行机构和传动机构特性,工程实用性不强。于存贵等[10]利用虚拟样机技术和舰船耐波性理论,对舰载火箭炮调炮运动进行动力学建模仿真,计算了某舰载火箭炮在舰船摇摆情况下调炮时方位和高低传动的受力情况,但舰载火箭炮系统建模过于简化,难以体现控制轴间速率干扰和力矩干扰的细节情况。叶镭[11]考虑了载体姿态扰动后,利用机器人建模方法,对无人炮塔的火炮控制系统建立了炮塔与火炮耦合动力学模型、坦克1/2车体悬挂系统模型及路谱激励,针对行进间火炮指向研究了非线性控制方法,但所建模型没有体现火炮与车体之间的关联性,仍然采用坐标变换位置的解算式稳定方法。在主战坦克火炮稳定控制器的研究方面,Karayumak[12]考虑了坦克身管弹性、传动系统各个环节的多自由度被控对象模型,研究了炮口速率观测和速率反馈稳定,干扰速率前馈补偿控制等方法。在不平路况和正弦路面对车体扰动的环境下进行仿真,火炮稳定精度达到了0.5 mrad,但系统控制并未考虑电机执行机构模型及车体姿态耦合扰动情况。在火力控制解算的坐标系选择上,郑岩等[13]研究发现,坦克火力控制采用大地坐标系下解算,能反映出目标与坦克之间的绝对运动关系,不但能提高对目标的预测精度,并且大大缩短了预测时间。
针对采用SINS测量火炮指向的自行火炮,充分利用SINS测量火炮指向和SINS陀螺测量火炮三轴向运动的优势,提出火炮在大地坐标系下完成稳定控制的方法。釆用Lagrange方法建立火炮、炮塔双轴与载体六自由度运动状态之间的耦合模型,并考虑炮塔和火炮回转中心与重心不重合等因素,用于验证稳定控制方案、系统控制策略等。最后建立系统的控制仿真模型,并验证了本文稳定控制方法的有效性。该方法为SINS测量火炮指向的火炮动基座条件下的通用稳定控制方法,不针对某种特定平台,不局限于某种可移动载体平台。
1 坐标系定义
火炮身管俯仰部分在高低驱动电机带动下在炮塔上作俯仰运动,炮塔在方位驱动电机带动下在运动载体上作方位回转运动,从而使火炮跟随控制指令指向目标,如图1所示。该俯仰和回转运动模型为双轴动力学模型,为了简化系统分析,假设火炮、炮塔联动状态下不影响车体运动状态。
由图1可知,本文所涉及的坐标系包括大地坐标系、平动坐标系、载体坐标系、炮塔坐标系和火炮身管俯仰部分坐标系。大地坐标系Ogxgygzg与大地固结不动,将原点Og定为载体初始质心处,Ogxg轴平行于水平面指向正北,Ogyg轴平行于水平面指向正东,Ogzg轴垂直水平面向下,载体在该坐标系下的坐标为(x,y,z). 载体坐标系Ocxcyczc的原点Oc位于载体摇摆中心(取重心处),Ocxc轴沿载体纵轴指向前方,Ocyc轴沿载体横轴指向右侧,Oczc轴垂直载体纵轴、横轴指向下方。载体在载体坐标系下的角速率坐标为(p,q,r),速度坐标为(u,v,w).平动坐标系Omxmymzm原点Om与载体坐标系原点Oc重合,Omxm轴与Ogxg轴指向一致,Omym轴与Ogyg轴指向一致,Omzm轴与Ogzg轴指向一致。炮塔坐标系Ohxhyhzh原点Oh为炮塔方位回转轴与方位回转平面的交点,Ohxh轴为火炮身管轴线向炮塔方向回转平面的投影指向弹丸射向,Ohzh轴沿炮塔方向回转轴指向下与Oczc轴平行,Ohyh轴垂直于Ohxh轴与Ohzh轴构成的平面向右。炮塔坐标系原点Oh在载体坐标系的坐标为(xch,ych,zch),炮塔质心在炮塔坐标系的坐标为(x′h,y′h,z′h).
火炮身管俯仰部分坐标系Opxpypzp的原点Op为火炮俯仰转动轴与火炮身管俯仰平面的交点,Opxp轴与火炮身管轴线重合指向弹丸射向,Ocyc轴与耳轴重合指向炮塔右侧,Opzp轴垂直于Opxp轴与Ocyc轴构成的平面指向下。火炮身管俯仰部分坐标系原点Op在炮塔坐标系的坐标为(xhp,yhp,zhp),火炮身管俯仰部分质心在火炮身管俯仰部分坐标系的坐标为(x′p,y′p,z′p).
根据以上坐标定义,从平动坐标系变换至载体坐标系的变换矩阵
(1)


(2)

(3)
(4)
(5)
2 火炮指向双轴动力学模型的建立
火炮稳定控制应考虑载体姿态变化对火炮指向运动控制的影响。根据第1节坐标系定义,炮塔坐标原点速度量为
(6)
炮塔质心的速度量为
(7)
火炮身管俯仰部分质心的绝对速度量为
(8)
炮塔的绝对旋转角速率为
(9)
火炮身管俯仰部分的绝对旋转角速率为
(10)
采用Lagrange方程法建立炮塔回转和火炮身管俯仰部分运动的动力学模型:
(11)

(12)
式中:ET=EThr+ETht+ETpr+ETpt;ED=EDh+EDp;EV=EhVg+EpVg+EpVk.ETht为炮塔质心动能:
(13)
式中:mh为炮塔质量。EThr为炮塔旋转动能:
(14)

(15)
ETpr为火炮旋转动能:
(16)

(17)
式中:Ch、Cp分别为炮塔、火炮转轴传动的黏性摩擦系数。EpVk为火炮的弹性势能:
(18)
式中:Kp为弹链、线缆等的弹性系数。EhVg、EpVg分别为炮塔、火炮身管俯仰部分的重力势能。
经过载体姿态的摇摆,且在炮塔和火炮调转后,炮塔和火炮身管俯仰部分在平动坐标系下的重力势能变化可表示为
EhVg=mhg[(-cosβcsinθc+sinβcsinφccosθc)x′h+
(sinβcsinθc+cosβcsinφccosθc)y′h+cosφccosθcz′h],
(19)
EpVg=mpg[(-cosβcsinθc+sinβcsinφccosθc)·
(xhp+cosεcx′p+sinεcz′p)+
(sinβcsinθc+cosβcsinφccosθc)·
(yhp+y′p)+cosφccosθc·
(zhp-sinεcx′p+cosεcz′p)-zch-zhp-z′p.
(20)
将(13)式~(20)式带入(12)式后整理得到稳定系统被控对象,即火炮指向双轴动力学模型:
(21)
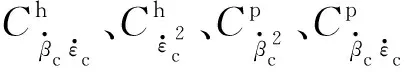
3 稳定跟踪控制系统模型
为了验证基于大地坐标系下的稳定控制方法,采用传统三环控制结构,各环控制器采用传统经典的比例积分(PI)控制方法,便于工程应用,如图2所示。图2中:ψref和θref分别为大地坐标系下的方位角和高低角控制主令;ihref和ipref分别为方位和高低电流环指令;ihm、ihs分别为方位主电机、从电机的电流环指令;Thme、Thse分别为方位主电机、从电机输出的力矩;Tpe为高低电机输出的力矩;θhmm、θhsm、ωhmm、ωhsm分别为主电机、从电机旋转角度和角速率;θpm为高低电机旋转角度;Thml、Thsl分别为主电机、从电机所受传动轴的负载力矩;Tpl为高低电机所受传动轴的负载力矩;Tc为炮塔作用于载体的三轴向力矩。虚线部分为可根据需要采用的速率干扰前馈补偿控制。
系统采用三相交流永磁同步电机作为执行电机,由成熟的空间矢量脉宽调制(SVPWM)控制功率电子绝缘栅双极型晶体管(IGBT)进行驱动。电流环采用id=0 A的矢量控制方法,利用电流环控制以得到所需力矩,其电流环PI控制器参数分别采用零极对消和期望时间常数设计方法。稳定环的PI速度控制器参数采用最佳中频宽度的设计方法[14],位置环采用PI控制与前馈相结合的复合控制。方位系统采用成熟的双电机拖动协调消隙控制,同时提高传动刚度,为实现末端速度反馈提供条件,具体可参考文献[15].

(22)
利用(22)式可避免对SINS航姿输出值求导或进行观测求解平动坐标系下的角速率。根据坐标系定义,平动坐标系与大地坐标系只是平移关系,对角度不产生影响。将大地坐标系作为稳定控制下静止不动的基准坐标系,利用统一在大地坐标系下的角度反馈和速度反馈可使高低和方位控制解耦。在已知ωp、βc、εc及其变化率时,可反向推算出炮塔ωh和载体姿态干扰角速率p、q、r,为干扰前馈补偿提供信息参考。虽然SINS实际航姿解算采用旋转矢量法,但该解算过程在控制中仍然可看作是积分环节,不影响控制系统的分析。也可对(22)式进行积分求解SINS航姿角,与(5)式求解火炮身管指向等效,也为SINS安装在载体上,为求解火炮身管指向提供了一种途径。
4 仿真验证

以干扰谱作为输入的六自由度载体运动状态模型,作为姿态扰动输入最为理想,但运动载体姿态频率响应函数不易得到。根据参考文献[16],选取扰动特征的最大幅值和主振频点作为扰动输入来验证控制策略是有效的。同时按参考文献[17],载体六自由度运动状态可作单频处理为:ψc=Aψcsin (fψct+εψc),θc=Aθcsin (fθct+εθc),φc=Aφcsin (fφct+εφc),Xg=10t+AXgsin (fXgt+εXg),Yg=0,Zg=AZgsin (fZgt+εZg). 其中,Ai、fi、εi(i∈{ψc,θc,φc,Xg,Yg,Zg})分别为载体航向、俯仰、横滚旋转运动前右下平移运动的幅值、频率和相位。仿真时,按参考文献[4]提供的一种重型车辆行进间典型车体运动数据进行仿真计算。三轴旋转幅值为7°,周期为2 s,频率为0.5 Hz,三轴同时大幅摇摆的干扰条件恶劣,故fψc=fθc=fφc=fXg=fZg≈3.14 rad,三轴平移按AXg=1 cm,AZg=3 cm. 而极限条件是指在给定伺服驱动功率限制和最大火炮射角条件下,稳定系统所能适应的最大扰动频率和幅值。极限条件不是恒定的,主要根据仿真需要进行调整,分别在典型条件和极限条件下进行火炮指向稳定和正弦跟踪仿真,其结果如下。
4.1 典型载体扰动条件稳定
姿态扰动模型具有随机性,为了简化,设定初始相位分别为εψc=π/20 rad,εθc=π/15 rad,εφc=π/6 rad,εXg=π/5 rad,εZg=π/3 rad. 大地坐标系下的火炮稳定主令分别为ψref=166.7 mrad(约10°),θref=1 266.7 mrad(约76°),得到典型载体扰动条件下火炮指向稳定控制曲线如图3所示,及其火炮速率稳定控制相关状态曲线如图4所示。
由图3(a)、图3(b)可知,采用传统的经典控制方法,火炮载体在典型扰动情况下,其方位指向稳定精度小于0.3 mrad,高低指向稳定精度小于0.2 mrad. 二者没有超调,而且二者的位置稳定没有相互干扰或耦合干扰。图3(c)、图3(d)分别为(23)式求得的载体坐标系下火炮方位和高低运动的轨迹实际值曲线,与应用(1)式、(4)式、(5)式将火炮指向从大地坐标系向载体坐标系转换得到的参考值曲线几乎重合,其稳态误差大小与稳定误差相当。只要在大地坐标下完成高精度控制,那么火炮在载体坐标系下的实际运行角度将自动跟踪坐标转换的参考值。火炮指向稳定主要依靠SINS陀螺反馈的速度稳定环实现,充分发挥稳定系统速度稳定环带宽远宽于位置环、响应快的优势。而传统高炮位置解算式稳定是火炮随动跟踪载体坐标系下的位置主令,间接实现火炮指向稳定。位置解算式稳定是利用随动位置环来实现稳定,显然其带宽不够,因此,传统高炮位置解算式稳定要求载体姿态扰动尽可能小。否则,将使本来就带宽很有限的随动无法跟踪载体剧烈的姿态变化,要实现目标的跟踪更难,这就是基于大地坐标系下的稳定要优于传统高炮位置解算式稳定的根本原因。
由图4可知,在火炮载体姿态干扰下,速度稳定环的反馈值能够很好地跟踪速度稳定主令,这是实现火炮指向稳定的前提条件。在稳态时,火炮在大地坐标系的角速率约为0 r/min,实现稳定。但此时在载体坐标系中电机的转速不为0 r/min,为了克服载体扰动,而以较高的转速做相应的适应性旋转。表明速度稳定环具有足够的响应带宽来克服载体航姿扰动。在射角θref为76°时,在稳态状态下,方位电机转速接近最大值5 800 r/min,方位电机稳态峰值电流几乎接近饱和值480 A,说明方位需要克服较高速度和力矩干扰,所需的功率已接近最大值,射角θref已不能再增大,再大就会超过系统调整的能力。电机三相电流值直接反映了电机轴负载变化。而高低电机稳态转速峰值不到1 000 r/min,高低电机稳态电流较小,峰值约为25 A,高低电机需要克服较小速度和力矩干扰,所需的功率相对较小。由此可知,高射角条件下的火炮稳定,方位电机转速高,角加速度大,方位稳定所需的功率也大。
4.2 极限载体扰动条件的稳定
减小扰动周期,增大干扰频率,为了保持输入干扰能量与典型条件下扰动能量相当,应减小干扰幅值。干扰参数设定为:Aψc=Aθc=Aφc=4°;周期设定为0.4 s,即频率为2.5 Hz;fψc=fθc=fφc=fXg=fZg≈15.7 rad;其他条件不变。射角θref为1 000 mrad(约60°),给定的方位功率不变,得到极限扰动条件下火炮指向稳定控制曲线(见图5)和火炮速度稳定控制相关状态曲线(见图6)。
由图5可知,即使车体扰动频率增加了5倍,火炮指向稳定精度和载体坐标中的理想值和实际值的重合度较之典型条件下变化不大,稳定精度的一致性较好,实现了方位和高低系统稳定控制独立。图6中速度稳定反馈也能够很好地跟踪速度稳定指令,电机旋转良好,能够适应干扰频率变化。图6(c)中方位电机在火炮指向稳定中的峰值电流接近最大值,而图6(d)中高低驱动在过渡过程中和稳态过程中所需的能量都大幅增加,表明高低轴受到的干扰力矩也大幅增加。
4.3 典型载体扰动条件下的稳定跟踪
在稳定基础上再叠加跟踪参量,系统所需的能量进一步加大,因此所适应的扰动能力进一步受到限制。典型载体扰动条件下,大地坐标系下方位和高低跟踪指令分别为ψref=1 000sin (2πt) mrad,θref=666.7+500sin (2πt) mrad,得到典型载体扰动条件下火炮指向正弦跟踪控制曲线如图7所示,及其火炮速率稳定控制相关状态曲线如图8所示。
由图7可知,在该扰动条件下的火炮指向正弦跟踪,方位跟踪精度不大于0.5 mrad,高低跟踪精度不大于1 mrad. 高低角在过渡过程中略有超调。在载体坐标系中,火炮运动实际值的轨迹依然能够很好地与参考值保持一致。方位稳定和高低稳定没有耦合。图8中,速度稳定反馈也能够很好地跟踪速度稳定指令,误差很小,几乎重合,消除速度扰动效果明显。高低电机的稳态电流峰值大幅增加,峰值约65 A,间接反映了在这种条件下高低负载扰动力矩增加。方位电机的电流曲线很明显在射角θref>666.7 mrad的区间比射角θref<666.7 mrad的区间要大。整个过程方位功率比较富余。
4.4 极限条件下的稳定跟踪
扰动条件下的正弦跟踪,既要稳定,又要跟踪,系统所需能量较大,其跟踪精度受火炮射角θref影响大,因此该极限条件的稳定跟踪与火炮指向纯稳定有所不同。经过大量仿真,幅值仍取Aψc=Aθc=Aφc=7°,将周期设定为1.4 s,频率为0.71 Hz,fψc=fθc=fφc=fXg=fZg=4.48 rad,控制器环控制参数不变,得到极限载体扰动条件下火炮指向正弦跟踪控制曲线如图9所示,及其火炮速率稳定控制相关状态曲线如图10所示。
由图9和图10可知,火炮指向在正弦跟踪中,其方位和高低稳态跟踪精度不大于1 mrad. 图9(a)中,在0.7~1.5 s之间出现了超差情况,此时在图9(b)中,射角θref在1 000 mrad的上方趋于顶点附近,方位电机输出电流趋于饱和,系统缺乏相应调整适应能力。与之对应的有图10(a)中的稳定速度曲线出现超调表明,此射角区间方位系统对高射角很敏感,射角稍微增大,功率很快达到上限。图9(c)中,火炮在载体坐标下的运动轨迹在相应时刻也出现了误差较大情况。而当射角θref<666.7 mrad时,方位系统所需的电流峰值下降至约105 A. 高低系统在调转过程中一直处于电流饱和状态,稳态由电流峰值也约为65 A,与图8(d)相当,由此表明高低系统对载体姿态扰动变化不敏感。通过比较图3、图5、图7、图9可知,高低和方位在角度稳定跟踪控制中,二者之间的耦合干扰不明显。
以上仿真验证了该稳定控制模型的有效性。后续将轮式车辆、履带车辆、两栖车辆行进间颠簸或摇荡的实际运动状态作为模型的随机干扰输入,来考核该控制策略在宽干扰频域范围内的适应性也是必要的。另外,传统减速机构是否能够满足该控制方案的使用要求还需进行深入研究。
5 结论
本文针对行进间火炮指向稳定跟踪问题,提出了基于大地坐标系下采用SINS作为火炮指向角度和调转角速率反馈的控制策略,并建立了系统模型,进行了稳定和正弦跟踪仿真验证,得出如下结论:
1)采用该方法实现了方位和高低两个稳定系统的独立控制,二者相互之间不耦合。
2)在大地坐标系下,对火炮指向的稳定跟踪控制精度优于传统高炮解算式稳定方式,且响应更快,能够适应较高的载体姿态扰动幅度和频率。
3)在火炮行进间且在高射角条件下,纯稳定火炮指向的使用条件比既要稳定又要跟踪火炮指向的使用条件更宽泛,后者对载体行驶或航行舒适性提出了较高要求。
4)采用Lagrange方法所建立的系统动力学模型能够有效地反映载体、炮塔、火炮之间的运动和动力学耦合关系,仿真运行过程中,模型稳定可靠,对系统控制策略的仿真验证起到了重要作用。

