冻融-渗流耦合作用下土质边坡稳定研究进展

汪恩良,靳婉莹,商舒婷,赵 曦

(东北农业大学 水利与土木工程学院，黑龙江 哈尔滨 150030)

研究表明，饱和-非饱和渗流是诱发边坡失稳的一个重要原因。经过多次冻融循环后，土体物理力学性质以及渗透特性发生了很大的变化。特别是在春融期，已融土和冻土层界面存在的一个高含水量、冰水混合的区域，水分在此处不断富集，降低了土体抗剪强度、加大土体融化深度、降低斜坡的整体稳定性，引起滑坡发生。为了对春融期滑坡机理进行研究，文章分别从冻融循环对土体渗透系数的影响，饱和-非饱和土渗流理论，降雨及融雪入渗过程，以及冻融过程中水-热-力多场耦合等多个方面进行了大量的研究和探讨，在前人研究的基础上进行总结与分析。

1 冻融循环对土体渗透系数的影响

1.1 饱和及非饱和土渗透系数

根据土体的饱和程度，一般将土体分为饱和土与非饱和土。在进行冻融土的渗透试验研究时，饱和土渗透系数一般采用“变水头渗透试验仪器”进行测量，渗透系数一般采用式(1)进行计算[1]。对于非饱和土的渗透特性，一般采用实测方法或用大量的试验数据确定经验参数，然后制定出土水特征曲线再得出非饱和土的渗透系数[2-4]。目前，对非饱和土的物理力学性能实验主要采用GDS三轴仪，它可以同时控制孔隙气压、孔隙水压、轴向和径向参数，很好的完成大多数线性变化的非饱和土试验[5-6]。当前常用的测量非饱和渗透系数的模型有Mualem模型、Genuchten模型以及Fredlund&Xing模型等[7-10]。而最常用的预测非饱和土渗透系数的解析函数是Van Genuchten-Mualem[11]，如公式(2)所示。

(1)

(2)

式中：Ks为饱和土壤导水率,cm/s；K(h)为非饱和土壤导水率,cm/s；a,A分别为变水头试管与试样的截面积,cm2；h1,h2分别为起始水头和终止时水头,cm；L为试样高度,cm；t为时间,s；Se为非饱和土的有效饱和度；m为土壤特征曲线的经验参数。

1.2 冻融对土体物理力学性质影响

作为一种强风化作用，冻融循环使土体颗粒重新排列严重影响土体内部结构[12-14]。对重塑土试验表明，冻融循环显著改变土体各层含水率。即冻融循环后土层上部含水量增加，下部含水量减少，而在试样的中间部位会出现含水量很大的土层[15-16]。对重塑土试验研究表明，冻融作用对土的干密度具有双向作用，即松散土密度增大，而密实土密度降低，多次冻融循环后，土体干密度会趋向于一个特定值，而这一特定值与土的种类有关[17-18]。研究表明无论冻融循环后土体密度如何变化，其渗透系数都会呈现增大趋势。多数研究都发现土体渗透系数在经过冻融循环后，会增大1～2个数量级，土的渗透性和密度经3～5个冻融循环趋于稳定[19-24]。

2 饱和-非饱和渗流理论研究

2.1 饱和-非饱和渗流方程

长期以来，众多学者针对饱和渗流研究相对较多，由于试验条件限制以及数值模拟技术的不足，非饱和渗流研究较浅。饱和-非饱和数值分析的基本理论是建立在广义达西定律式和质量守恒方程上的Richards方程式，如式(3)和式(4)所示[25]。

v=kJ

(3)

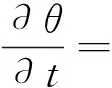
(4)

式中：v为渗透流速,cm/s；k为渗透系数,cm/s;J为渗透坡降；θ为土体含水量；t为时间,s；ψ为土水势,kPa。

对于非饱和渗流计算，其参数的确定极其重要。1980年Van Genuchten等[26]提出了VG模型，随后严飞等人[27]在2004年提出“双参数VG模型”用来确定非饱和渗流参数。在无法开展试验的条件下，可以选用函数曲线来替代非饱和渗流试验所测得的数据线性对应关系，用VG模型参数的代表值进行计算，计算式如公式(5)和公式(6)。

(5)

(6)

式中：α,n,m为土壤特征曲线的经验参数；h为压力水头,cm；θ为土壤含水率；θs为土壤饱和含水率；θr为土壤残余含水率。

2.2 饱和-非饱和渗流研究方法

对饱和-非饱和数值分析研究方法中，常用的方法包括有限差分法和有限单元法。随着计算机技术的进步，基于有限差分法的FLAC软件也在饱和-非饱和渗流分析中得到了越来越广泛的应用[28]。廖红建[29]以Morgenstern-Price条分法和极限平衡原理为基础对坝坡产生滑移的最小安全系数变化规律进行了分析，从而得出渗流-滑坡的内在联系。吴良骥等[30]提出的有限差分法数值模型以及相应的应用程序，这种方法不仅具有Narasimhan提出的积分有限差分法的优点，并且应用了辛甫生数值积分提高了质量平衡精度。朱学愚等[31]将SUPG有限元方法应用于非饱和流动的Richards方程，并导出了数值表达式，对一维入渗问题进行了数值计算。陈虹等[32]提出一个简易的曲线拟合方法，从有限的观测试验中获取所需参数，这种程序可以应用到具有复杂地质边界条件的实际渗流工程。随着试验方案以及试验仪器的不断改进，人们对于饱和-非饱和区中渗流问题的数值模型的研究愈加趋向于完善。

3 降雨及融雪入渗模型研究

3.1 降雨入渗理论模型研究

一般情况下春融期降雨量较小，但春融期坡面土壤尚未完全融化，由于土壤的单项冻结双向融化的性质，在边坡内部会存在一个解冻不完全、高含水率、渗透性差的薄弱带，雨水入渗很容易破坏边坡的应力平衡体系，此时的降雨很容易导致土壤流失或者滑坡的发生。对于冻土边坡，土体内大部分水是以冰的形式存在的，所以在降雨初期入渗量较少，温度较高的雨水入渗使得固态冰融化，降雨入渗率随之增大，直到边坡土体达到饱和产生地表径流，降雨入渗量随之减小，然后趋于稳定。

降雨型边坡失稳数值模拟研究的关键是从理论上揭示雨水入渗后边坡应力的变化过程、雨水在边坡中的渗透特性和渗透过程，以及暂态附加水荷载问题等[33]。王佳佳[34]等利用GIS平台得到滑坡土体饱和因子在时间和空间上的分布情况，并进行了水文模型与无限斜坡模型的耦合。Chue Y S[35]利用GIS平台描述了滑坡潜在滑坡图，并研究了极端降雨事件对斜坡滑坡和滑坡发育特征的影响。唐扬等[36]以Mein-Larson降雨入渗模型为基础，通过假设初始土体含水率随深度(坡面垂直的方向)呈线性分布，推导出一种适用于初始含水率不均匀分布的滑坡降雨入渗函数。钟佩文等[37]研究得出降雨入渗使土体的抗剪强度显著降低，边坡稳定安全系数随降雨入渗的进行而逐渐减小。王建新[38]通过对降雨非饱和入渗过程的水势描述及理论模型研究，提出一种新的边界条件处理方法，并推导出降雨自由入渗和压力入渗模型。常用的降雨入渗模型有Green-Ampt积水入渗模型、Horton入渗模型以及著名的Philip入渗公式[39-40]。其中Green-Ampt入渗模型可表示为：

i=Ks(1+Hm/Lf)

(7)

(8)

式中：i为土壤入渗率,cm/s；Hm为湿润峰处的平均吸力,m；Lf为概化的湿润峰深度,m；hd为进气吸力。

3.2 融雪入渗理论模型研究

与降雨不同，积雪融水引起边坡失稳是一个长时间的过程，而融化后的雪水绝大部分入渗地表松散沉积物，径流较少。影响融雪入渗的因素有很多，除温度外，地表下垫面情况也是影响融雪入渗的一个重要因素。融雪入渗是一个复杂的过程，寒区土壤包气带融雪入渗过程可分为四个阶段，即积雪层入渗、包气带融层入渗、包气带冻层入渗、冻层至饱水带的入渗[41-42]。逄淑然[43]对寒区春季融雪入渗规律进行监测试验与分析，研究了不同阶段融雪水入渗深度与入渗特征。魏召才[44]通过能量平衡方程和水量平衡方程数值模拟，建立了一个具有物理基础的基于单点双层融雪模型；Lilbak G等[45]提出一种关于积雪离子入渗的理论模型，该模型表明离子浓度与浸润体积之间的关系是非线性的，具有正协方差。俞鑫颖等[46]、房世峰等[47]基于遥感(RS)和地理信息系统(GIS)技术基于能量平衡和水量平衡原理对融雪产汇流进行模拟计算，提高了模拟的精度；余文君等[48]、孟现勇等[49]以SWAT模型(土壤和水评估工具)改善了融雪径流的计算方法，提高该物理模型整体模拟精度。孟现勇等指出能量平衡融雪模型参数较多、模型复杂但精度较高，温度因子法融雪模型结构简单、合理确定参数后效果更好；付强等[50]、李天霄等[51]对融雪过程进行分析，得出积雪阻碍了环境因素对于土壤水热迁移过程的影响，在一定时间段内，融雪入渗会有延后现象。钱晓慧等[52]对寒区冻融土壤的各项参数进行监测，指出边坡渗透系数以及边坡安全系数与积雪深度、边坡坡度和气温温度相关。谭娟[53]针对多种不同水保措施坡面观测其融雪、侵蚀特征，指出对于融雪侵蚀，生物措施>工程措施>耕作措施。

4 多场耦合模型研究

冻土体在冻融过程中的热量传输、水分迁移与相变过程并不是由单独某个因素所造成的。冻融循环过程中土体的应力与变形计算与温度和含水量有着密切的关系。应力、变形与水、热是相互影响的，在进行冻融对渠道边坡稳定性分析计算中应考虑水、热、力的耦合计算[54]。

武建军等[55]做了饱水状态下冻结土体的渗流、温度、应力耦合机理分析。金栋[56]基于水、热、力耦合的FLAC 3D温度场分析基本原理，模拟寒区边坡的冻融循环过程，得到相应的安全系数。徐轶等人[57]借助COMSOL对三维渗流场进行数值分析，综合考虑渗流、应力、温度，实现了三场(THM)耦合。许孝臣等[58]则针对单裂隙渗流实现了渗流-应力-温度-化学四场耦合过程，模拟了地应力、温度、渗透性较高，水化学环境复杂条件下的裂隙渗透特性的变化规律。王世梅等[59]利用GeoStudio seep/w与slope/w两个模块分别进行渗流分析与稳定性分析，得到了水位升降速率和边坡稳定性的关系。何敏等[60]研发出一种可以用于冻土中水、热、力三场耦合分析的平台3GEXFEM，该模型能全面考虑冻土中土骨架、冰、水三相介质水、热、力与变形真正的耦合作用的数理方程，分析得到的温度场、水分场与变形场与试验结果较一致，具有较好的应用前景。

在实际工程中，多场耦合数值模拟难度仍然较大，尤其是在春融过程中，上层已融土和下层未融土交界面处的物理力学性能尤其复杂。这要求我们不断地改进实验方案并在试验设计初期考虑更多的因素，以得到更加完善准确的模拟参数进行多场耦合模型的研究。

5 基于强度折减法土质边坡稳定研究

5.1 强度折减法原理

由于土质边坡发生失稳破坏过程，往往在边坡内部形成一塑性区，随着塑性区的不断扩大，贯穿整个边坡，边坡随之失稳。因此目前土质边坡稳定性分析方法主要基于岩土的弹塑性理论，考虑边坡土质的应力应变状况进行分析。有限元强度折减法在边坡稳定性分析中有着非常广泛的的应用，它可以利用多种概化模型边坡求解边坡的安全系数[61]。强度折减法的基本原理如公式(9)所示：

c′=c/Ftrial,

φ′=arctan(tanφ/Ftrial)

(9)

式中：c,φ分别为黏聚力和内摩擦角;Ftrial为强度折减系数;c,φ分别除以Ftrial得到一组新的c′和φ′然后作为新的参数进行运算，直到运算不收敛，此时对应的Ftrial被称为坡体的最小稳定安全系数。

5.2 强度折减法在边坡稳定性研究的应用

寇天等[62]基于ABAQUS软件，通过动态非等比例的双强度折减法理论，研究出一种收敛快速、边坡稳定性系数和位移均小于传统强度折减法的动态非等比例的双强度折减法。王俊杰等[63]基于强度折减有限元的非均质土坡失稳判据分析了非均质土坡失稳破坏的过程，提出了以特征点位移矢量突变结合塑性区贯通的失稳判据。江胜华等[64]提出针对特征点位移突变的变步长折减法，探讨了强度折减系数的折减幅度，并对基于位移变化率的强度折减有限元法给出了相关的建议。张永明等[65]基于强度折减有限元法的土质边坡稳定性分析，将强度折减有限元法与ABAQUS软件相结合，借助ABAQUS建立了平面破坏型边坡有限元分析模型。赵炼恒等[66]基于双强度折减策略的边坡稳定性分析方法探讨，研究结果表明，边坡稳定性影响因素众多，抗剪强度参数c′和φ′的折减系数之间不存在唯一确定的函数关系。王创业等[67]通过强度折减法在边坡稳定性中的对比分析，研究表明双强度折减得到的临界滑动面范围要比等比例折减的范围大，在不同安全系数定义中采用c-tanφ曲线分析得到的结果，物理意义更明确、更符合边坡实际情况。用强度折减法分析边坡稳定性时，不需要事先假定滑动面的位置和形状，因此具有较强的适用性。

6 结论与展望

(1) 冻融作用一定程度上破坏土体的结构，使土体变疏松，渗透性增强，在冻融循环过程中，周期性的冻结与融化持续改变着土体内部结构，使土的孔隙比与渗透性发生相应的变化。冻融循环后土样孔隙比随冻融次数增加呈指数增加趋势，但经过多次冻融循环土体结构强度逐渐趋向于稳定的残余强度，这时土体的孔隙比与渗透系数逐渐趋于稳定。

(2) 饱和-非饱和渗流参数大多数是通过实验室试验测得的，这与实际工程中测得的参数不完全一致，针对这方面还需进行更多的现场测量以得到更多的实测资料，使计算结果更加的具体可靠。对于室内模型试验时，需要结合现场勘测的工况进行分析。目前对渗流场的研究大多数是对饱和渗流场进行研究，而没有进一步研究冻融期非饱和渗流场，该项工作有待后续进一步加强。

(3)春融期融雪入渗引起边坡失稳涉及到水动力学、土工程学、计算机技术等多个学科。融雪过程复杂且影响因素极多，不同时间段融雪入渗过程不尽相同。在进行模拟计算的同时，更应该结合现场实测资料，针对不同实际工况进行分析。

(4)冻融循环过程中应力、变形与水、热之间相互影响。目前寒区渠道多场耦合数值模拟难度仍然较大，尤其是在春融期，冻土的渗透系数很小，特别是饱和状态下冻土渗透系数可忽略不计。春融期坡面土壤内部会存在一个解冻不完全、高含水率、渗透性差的薄弱带，已融层水大部分受重力作用积蓄在不透水界面上，上层已融土和下层未融土交界面处的物理力学性能尤其复杂，这也是未来需要解决的又一难题。

(5)研究表明渠基土体在冻融循环后结构损伤，或者组成颗粒发生重新排列，导致土体抗剪强度发生变化。但c,φ值变化不是同步的，未来研究可以着重于抗剪强度冻融损伤因子的有限元不等比例折减系数法计算c′和φ′值，根据强度折减法分析边坡稳定性，分析渠基土体在冻融循环后结构损伤量以及土体抗剪强度发生的变化。