极限分析法在公路边坡稳定性计算分析中的适用性研究
王志远
(山西交通控股集团有限公司大同南高速公路分公司,山西 大同 037004)
土边坡稳定问题一直是岩土工程界研究的难点与热点[1],普遍存在于各种工程项目中。在国家“一带一路”政策的引领下,在建或运营的公路里程日益增多,随之公路沿线形成了大量的边坡,边坡的稳定性不仅会直接危害道路的安全运营、行车安全,还会造成大量的经济损失[2]。
由于受到水位降落和降雨等复杂因素的影响,很难明确确定边坡的安全系数[3]。虽然目前有诸多分析边坡稳定性的方法,但是极限平衡法通常边坡划分为土条,且假定滑动面为圆弧面,这与实际情况存在偏差;有限元、离散元等虽然计算较为准确,但是计算过程较为繁琐、耗费时间长、理论化要求高,很难在实际工程中大量推广应用。因此有必要探究新的数值稳定性分析方法,使之能够用于公路边坡的稳定性分析。
基于上述需求,本文旨在利用极限分析法对公路工程中常见的倾斜分层软弱夹层土坡稳定性进行分析,以验证极限分析法在分析边坡稳定性理论计算方面的适用性,并探究边坡稳定计算新方法。
1 极限分析法原理与计算软件
1.1 极限分析法原理
极限分析法运用了弹塑性力学中的上、下限定理论来求解边坡的稳定性问题,这样就可以确定真实解的范围。上限的方法也称为能量法,通常需要假定一个滑动面,并将大的土体划分成若干小的土块,通常把土体视作理想刚塑性体,然后建立一个协调位移场。利用虚功原理,计算滑体处于极限状态时的极限承载力或稳定安全系数。极限分析法的下限解方法在计算过程中通常需要构造一个合理的静力许可应力场,一般情况下可以用应力柱法或者应力不连续法等来求得问题的下限解,下限法计算得到的解比实际的解要小[3-4]。
这种方法采用了屈服准则的概念,考虑了与应力-应变关系相适应的流动法则。用于斜坡稳定性分析时,不必像条分法那样做出假设,因而具有物理概念清晰、应用简单等优点。极限分析法是以正交法则考虑了土的应力-应变关系后建立的一种塑性分析方法。

图1 体积V和边界ST、SU
1.1.1 极限分析法中一些基本概念
1.1.1.1 静力许可应力场
静力许可应力场[4](简称静力场)是指满足下列条件的应力场:
c)在力边界ST上满足应力边界条件
1.1.1.2 运动许可速度场
b)在速度边界SV上满足边界条件:=V,通常Vi=0;
1.1.3 虚功原理
在荷载作用下处于平衡的变形体,若给出一微小的虚变形(或位移),则由于外力(或荷载)所做的虚功必等于内力(或应力合力)所做虚功。即:

1.1.4 下限定理
如果可以找到一种遍及整个物体的应力分布σij与应力边界ST上的作用荷载Ti相平衡,且σij又在屈服面以内,则物体在荷载Ti和Fi作用下不会发生破坏。也就是说,在与任何稳定的静力许可应力场相平衡的荷载中,选出其中最大者,它就是破坏荷载(极限荷载)的下限。
1.1.5 上限定理
1.2 LimitState软件简介
LimitState是由英国谢菲尔德大学开发的用于分析岩土稳定性问题软件,该软件的计算方法是极限分析法,在分析过程中采用非连续面优化布局使滑动面不加人为限制自由生成来直接确定稳定临界状态的失效机制[5]。
1.2.1 LimitState的特点
a)LimitState一个突破性的新产品,用于分析岩土稳定性问题。LimitState带来了一种更全面的解决方案,而不是沿用以往传统简单依靠手算的方法,比起有限元分析方法而言,更加易于使用。
b)与传统的岩土稳定性分析工具不同,使用LimitState可以更轻松快捷地进行分析几乎所有类型的岩土稳定性问题,包括把边坡稳定性、挡土墙、基脚、隧道测算的多项工作整合起来,进行同步分析处理真正的失效机理与安全边界机制,而无须事先确定问题的类(不需要做任何假设,也不需要假定滑动面的形状,就能得到安全系数,还能直观地得出边坡破坏的类型与性状)。
c)确定性方案,比传统的自动手工计算类型的软件得到的结果更加精确。
1.2.2 LimitState的计算原理
LimitState利用非连续面优化布局进行计算,具体的计算流程如下:
a)用结点把区域离散化(图2a和图2b);
b)将潜在的滑移线不连续地把结点连接起来(图 2c);
c)采用优化分析来识别临界失效机制的不连续滑移线(图2d);
d)计算得出对应的安全系数。

图2 LimitState软件计算流程
2 边坡稳定性分析适用性研究
2.1 工程概况
图3为山西吉河高速中一倾斜分层边坡,从表1参数可知,该边坡上下两层土强度较高,而中间夹着的土层强度小,为存在软弱夹层的边坡体,在实际工程中,该类滑坡最不稳定且其稳定性最难以预测[6-7]。在本案例中不考虑孔隙水压力。边坡土体各土层的参数见表1,边坡的几何尺寸见图4。

图3 吉河高速倾斜分层

表1 土体参数
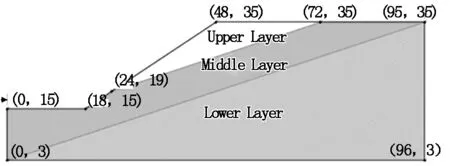
图4 边坡几何形状与尺寸
2.2 计算分析
为了验证基于LimitState软件的极限分析法在边坡稳定计算中的可靠性,本节中选用前人用其他方法的计算结果作为参照,进行对比分析。
用表1中土体的参数与图3中边坡的几何尺寸在LimitState.geo、Geoslope软件中分别建模,用极限分析法(LimitState.geo)与极限平衡法(Geoslope)分析所得结果如图5。


图5 极限分析法与极限平衡法失稳破坏模型
用LimitState.geo和Geoslope软件分析所得到的安全系数与已有的安全系数见表2。

表2 本文分析所得安全系数与已有安全系数
在文献中作者用Janbu、Bishop方法计算得到安全系数0.410、0.421。在本文中笔者借助Geoslope软件,采用与文献中对应的方法计算得到安全系数0.408、0.420。虽然两个数值有一定差值,但在误差的允许范围内,上述两个数值是十分接近的。比较上述计算数据,当结点密度Nodal Density=500时,所计算出的安全系数0.443大于Geoslope计算所得安全系数0.421、0.408,但在误差允许范围内。所以,在Nodal Density=500时用极限分析法分析,既能满足安全的要求同时相对于用极限平衡法也可以节约成本。
从图5可以看出:在用极限分析法计算时,随着结点密度的增加滑动面形状逐渐由折线形越来越趋近圆弧形。在Nodal Density=1000时,用LimitState计算得滑动面形状由圆弧面与折线共同组成。与Geoslope计算的滑动面形状相差较大。
3 结论
从上述案例的分析结果可以看出:
a)本文用LimitState(极限分析法)计算得到的滑动面更加接近于实际情况。
b)得到的安全系数与已有的文献中用各种极限平衡法计算出的安全系数接近。证明了用极限平衡法所计算得到的边坡稳定性安全系数适用。
c)用LimitState软件(极限分析法)分析边坡稳定性,当结点密度Nodal Density=500时分析得到的安全系数一般都略大于极限平衡法计算得到的安全系数,这表明用极限分析法得到的计算结果既能满足边坡稳定的安全防护性的要求 同时相对于用极限平衡法也可以节约资金。有利于在当前经济节约型的公路工程建设中使用。
d)本文选取了边坡案例,用数值模拟的方法验证了极限平衡法的理论优势,该方法在实际工程中的具体表现则有待在实际中验证。

