单级PFC反激式开关电源设计

李晓晖 赵 杰 苏亚东 张玉峰 郑 凯

（1.皖北煤电集团有限公司，安徽淮北232097；2.徐州凯思特机电科技有限公司，江苏徐州221116；3.中国矿业大学电气与动力工程学院，江苏徐州221116）

0 引言

开关电源的相关标准中对于降低电流谐波及提高功率因数有着明确的要求，这使得PFC技术在开关电源中的应用越来越广泛。有源PFC技术相比于无源PFC技术具有响应快、动态效果好等优点而受到广泛研究。一般含有PFC功能的开关电源采用两级PFC结构，一级为功率因数校正级，一级为电压变换级，两级结构导致系统结构复杂、成本较大，据此，单级PFC结构应运而生[1-5]。

本文针对单级PFC反激式开关电源，分析了其在CCM下FOT控制系统的工作原理，完成了系统的大信号分析，按照大信号分析的结构，设计了系统电路及变压器参数，完成了系统仿真，验证了该系统的可行性。

1 单级PFC反激式电路基本结构

图1是一种单级PFC反激式变换器的结构，由于省去了原边的电感、整流二极管和电解电容，简化了电路结构，使控制方法变得简单。由于输入端采用了小容量的电容，只能滤除输入电压中的高频谐波。输入电压经过电容后还是正弦半波。PWM控制器对输入、输出电压采样，在其内部计算出电流基准，再和电流采样值进行比较，根据比较的结果控制Q2的通断，完成功率因数校正。

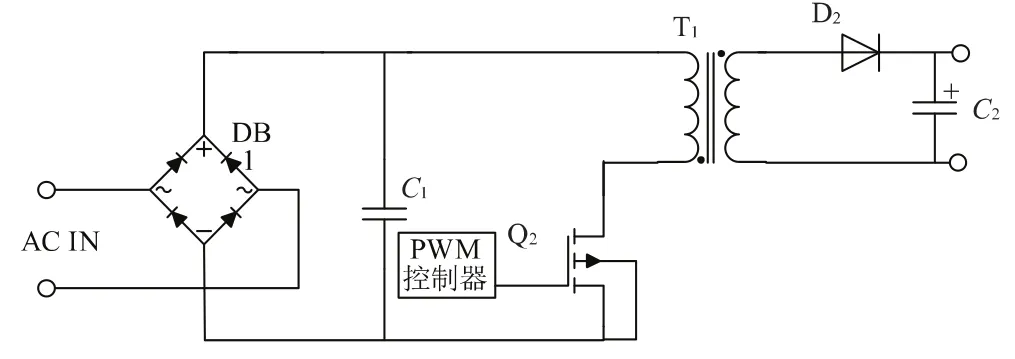
图1 无输入大电容的单级PFC反激式变换器结构

2 FOT控制模式单级PFC反激式变换器大信号分析

本节首先分析了FOT控制的单级PFC反激式变换器的工作过程，然后对系统进行了大信号分析，并对系统中各参数及其之间的能量关系进行了研究，最后，根据这些参数给出了变压器的设计方法。

2.1 FOT控制模式工作原理

图2为FOT控制单级PFC反激式变换器的系统框图。输出电压Vo经过R3、R4和隔离电路进行电气隔离后进入电压环。乘法器的作用是构建完整的电流基准，该基准是一个与输入电压同相位的正弦半波，所以其输入分别为电压调控信号和输入电压相位信号。开关管的关断条件是采样电阻上的电压高于乘法器的输出电压。开关管的导通由Toff产生电路控制。

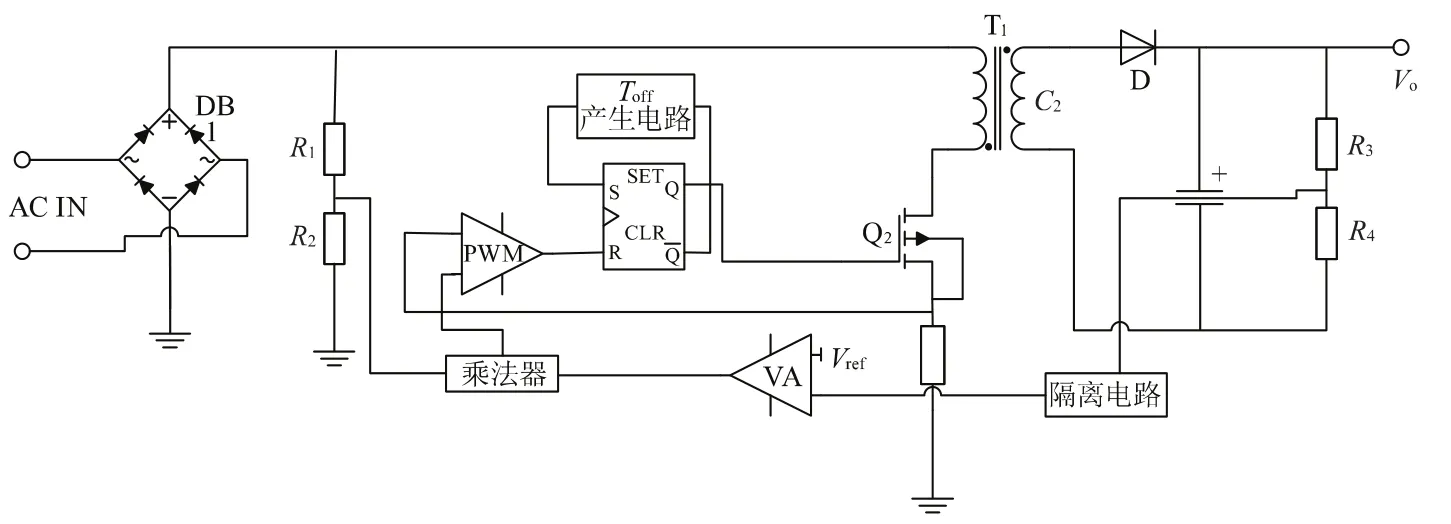
图2 FOT控制单级PFC反激式变换器系统框图

FOT控制变换器的输入电流和PWM波形如图3所示。当开关管导通时，输入电流线性增加，关断期间，可以将次级电流和电压等效到初级侧，等效输入电流在此期间线性下降。由于次级反射电压不变，且开关管关断时间不变，所以等效的输入电流下降值也不变，其大小可由式（1）确定：

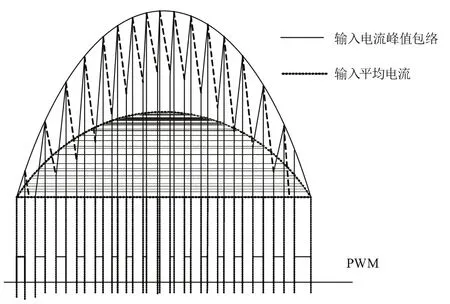
图3 FOT控制模式变换器输入电流及PWM波形

在输入电压较小时，变换器工作在DCM模式。随着输入电压的增大，变换器从DCM向CCM过渡。由于输入电压的波形是正弦半波，在一个半波内，变换器先工作在DCM，然后工作在CCM，最后又回到DCM。所以，在一个正弦半波里存在一个DCM和CCM的临界电压，这个电压对应的相角叫做临界相角θT。当输入电压相角在（0，θT）以及（π-θT，π）时，变换器工作在DCM模式；当相角在（θT，π-θT）时，变换器工作在CCM模式。

当输入电流在开关管开通期间上升值等于关断期间的下降值时，即变换器工作在BCM。假设此时输入电流峰值为IPKpri，则：

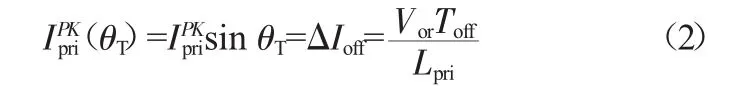
可求得临界处的相角为：

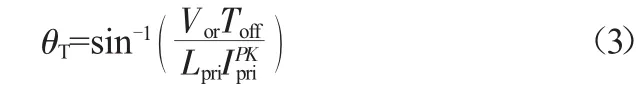
当变换器在DCM时，开关管的导通时间不变。所以此时变换器的D和fsw都是常数。当变换器在CCM部分，变换器的D和fsw由线电压峰值和瞬时值决定。开关频率关于相角θ的函数为：

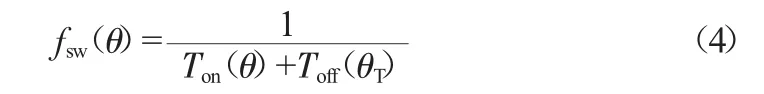
2.2 FOT控制模式的能量关系

在DCM部分，输入电压和负载不变，变换器的开关频率也不变。此模式下，输入电流的平均值为：

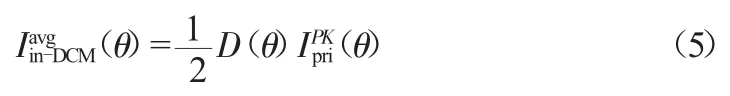
FOT控制模式处于DCM模式下和峰值电流控制模式处于DCM模式下情况相同，系统工作在此模式下的功率因数不可能为1。

在CCM模式下，初级侧电流纹波为：

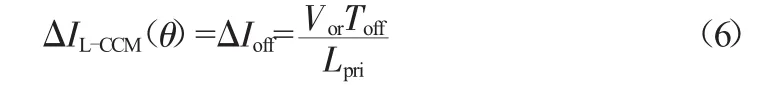
所以该模式下的输入电流的平均值为：

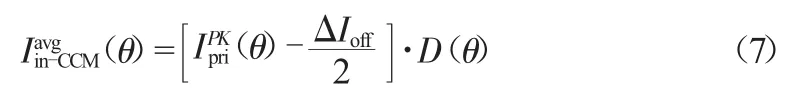
综合式（6）和式（7），可得：

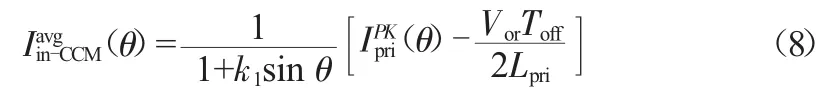
在一个输入电压正弦半波内，变换器经历了三个阶段，这三个阶段的输入功率分别为：

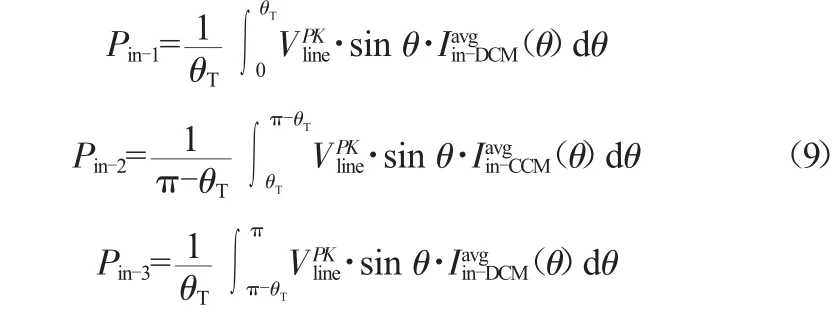
由于DCM部分过程较为短暂，且CCM部分在输入电压相角较小时的电流与DCM相差不大，所以输入功率可简化为：

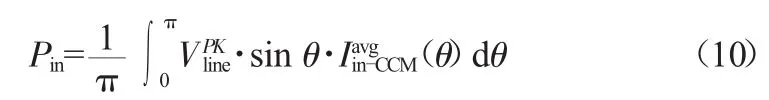
将式（5）和式（8）代入式（10）可得：

在已知输入功率的情况下，输入电流峰值的表达式如下：

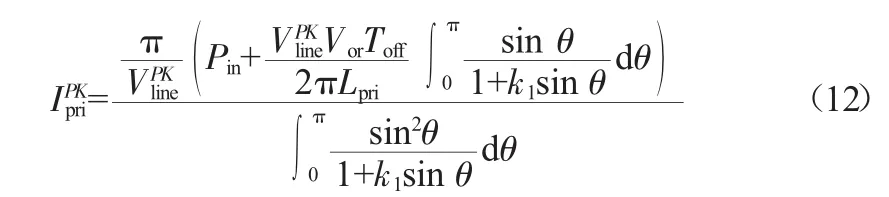
2.3 系统电路参数设计

2.3.1 变压器设计

虽然初级电感量与输入电流纹波成反比，但也不能一味地减小电流纹波，初级电感量过大会使变压器体积过大，选取初级电感量为400 μH。

由于初次级绕组耦合系数较高，所以有：

使用耐压为650 V的功率MOSFFET，根据反激式变换器的输出输入电压关系，可得：

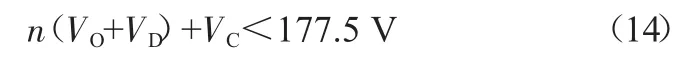
VC一般被RCD钳位在次级反射电压的1/2。根据式（14），反射电压最大为120 V。由于VO为19 V，VD为1 V左右，所以变压器匝比最大为6。仿真时取匝比为5，代入式（13）中可得变压器次级电感量为16 μH。

2.3.2 初次级电感电流峰值计算

当匝比为5时，次级反射电压为100 V，由式（12）可得初级电感电流峰值为5 A，次级电感电流峰值为25 A。

2.3.3 钳位网络的设计

变压器的漏感造成的过电压尖峰可以受到RCD钳位网络（图4）的限制。选择适当的电容及电阻值，以便其具有指定的过电压ΔV（一般取反射电压的一半），使其关断时不会超过MOSFET的额定电压。

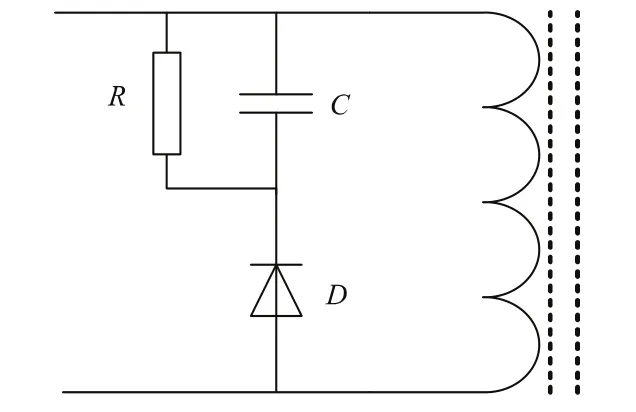
图4 RCD钳位网络

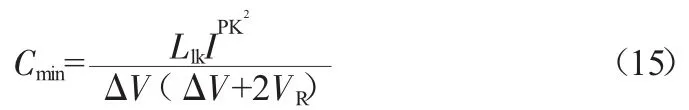
Llk为变压器的漏感。电容器要经受大的电流尖峰，因此其应该是具有聚丙烯或聚苯乙烯薄膜电介质的非常低的ESR型。

最小电阻值可以通过在开始时施加电容上的电压来得到：

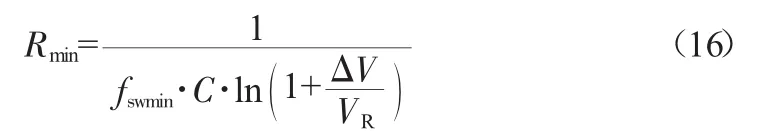
3 系统电路仿真

采用L6562N器件，该模型ZCD引脚的阈值电平为1.6 V，可得关断时间为：

取Ct=620 pF，Rt=10 k。选择Ca=220 pF，Ra=3 kΩ。

输出电压通过r12和r13分压后进入TL431的输入端，由于在闭环运行时，分压电压在2.5 V波动，所以有：

由于输出电压为19 V，r12为22 kΩ，所以r13为3.33 kΩ，由于在实际中没有这样阻值的电阻，所以取r13为3.3 kΩ。在输入为110 V/50 Hz，负载为3.8 Ω，对系统进行瞬态仿真，输入与输出电压波形及系统稳定时的输入电压与输入电流分别如图5和图6所示。

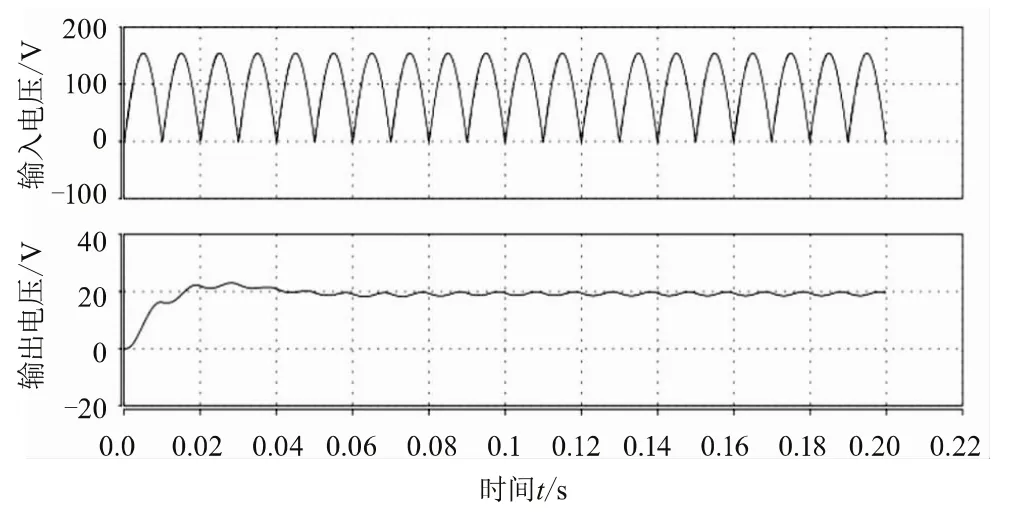
图5 110 V AC输入下输入与输出电压波形

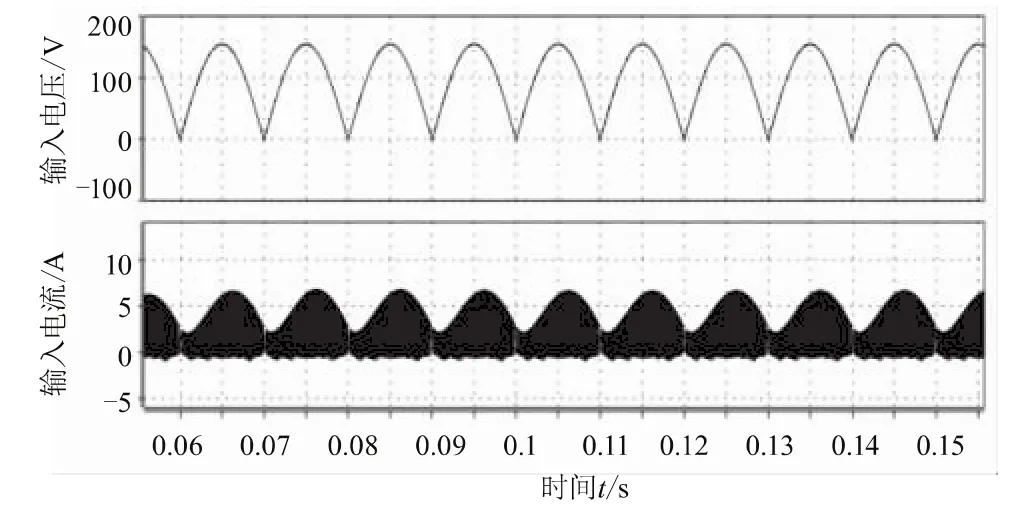
图6 系统稳定时的输入电压与输入电流

从图5中可以看出，输出电压两倍频纹波，其波动幅度为1.5 V，约占输出的7.8%。从图6中可以看出，输入电流峰值紧紧跟随输入电压，系统实现PFC功能。

为了看到输入电流的各次谐波，首先平滑一下电流信号。在仿真电路中，r7为10 kΩ，C9为10 nF，其截止频率为1.6 MHz，远大于开关频率，所以C9上的电压可以反映输入电流的平均值。对C9上的电压进行傅里叶分析后，由图7可以看出，各次谐波所占的比例非常低，可见电流波形失真较少。

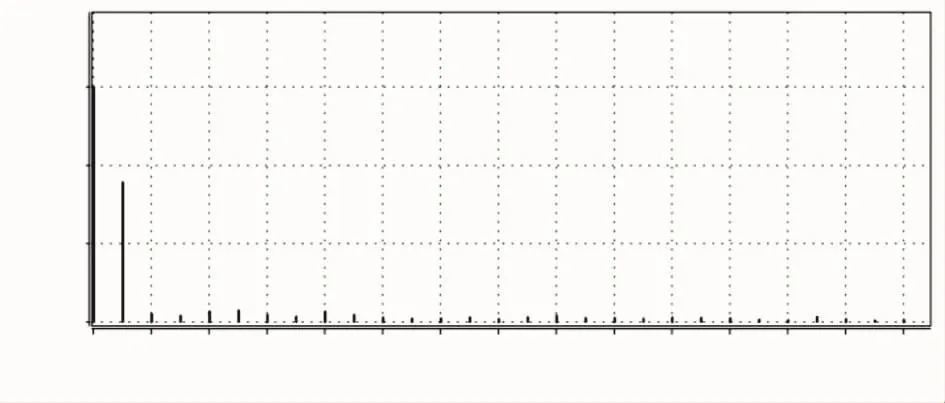
图7 110 V输入下电流谐波

在输入为220 V/50 Hz，负载为3.8 Ω，即输出平均电流为5 A的条件下，对系统进行瞬态仿真，输入与输出电压波形和输入电压、输入电流及采样电阻上的电压分别如图8和图9所示。

由图8可知，通过输出电压稳定在19.1 V。测量的100 Hz的纹波电压的峰值为1.8 V。从图9可以看出，在220 V下系统的输入电流依然能够紧紧跟随输入电压。

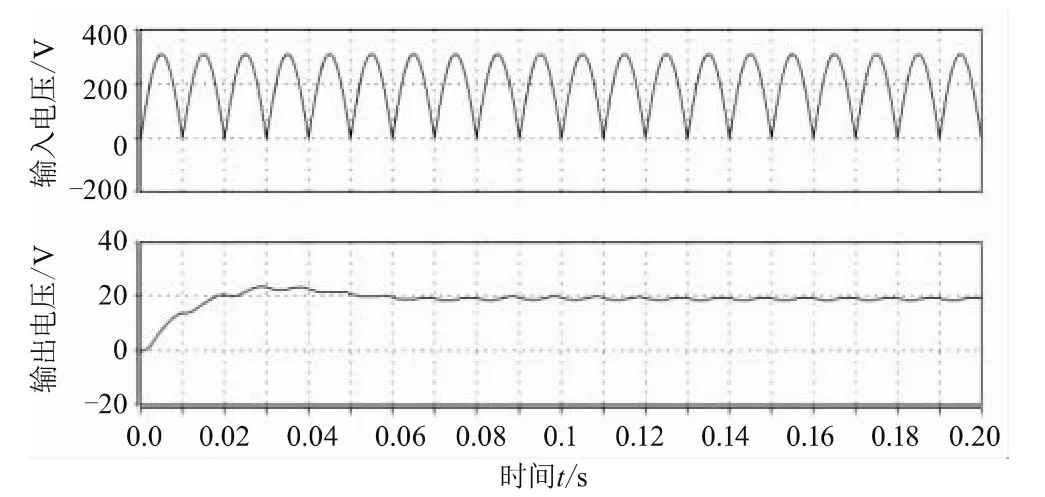
图8 220 V AC下系统的输入与输出电压

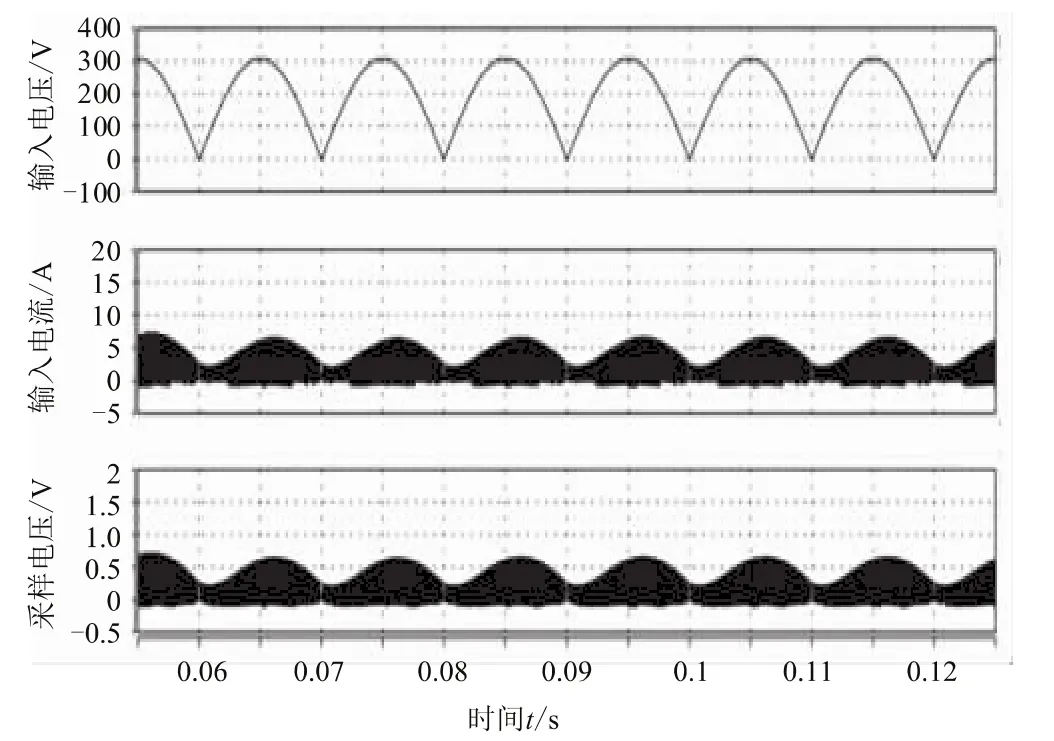
图9 220 V下的输入电压、输入电流及采样电阻上的电压

4 结语

本文研究了固定关断时间的单级PFC反激式变换器，在对临界模式和连续模式分析的基础上完成了对固定关断时间控制模式的大信号分析，设计了系统电路。这种结构的电路结构和控制方式简单，成本较低。本文的研究成果对于单级PFC反激式变换器的设计具有一定的指导意义。