基于遗传算法优化的阴性选择算法在故障检测中的应用
王义东 刘天羽
(上海电机学院电气学院,上海201306)
0 引言
1994年,知名美国学者Forrest等[1]提出了阴性选择算法(Negative Selection Algorithm,NSA),作为人工免疫系统中的核心算法之一,阴性选择算法通过模仿成熟T细胞的自我审查过程,训练出来的成熟检测器具有只识别非自体异常数据的能力[2]。但是由于NSA生成的检测器不能完全有效覆盖非自体空间,存在“黑洞”问题,检测效率不高。
本文采用遗传算法来优化NSA生成的检测器,提高其检测效率。
1 阴性选择算法
在生物免疫识别系统的阴性选择原理的基础上提出的阴性选择算法,被广泛应用于故障检测、垃圾检测、病毒检测等方面。
首先用字符串分别代表自体集(S)和非自体集(N),然后通过设定好的匹配阈值和匹配规则等参数随机生成长度为L的字符串d,字符串d即表示未成熟的检测器。根据设定的匹配阈值及规则,令d分别与自体集S中的元素进行匹配,若匹配则继续生成随机字符串,若不匹配,则将d加入到成熟检测器集D[3]。成熟检测器D用于检测非自体集N,若匹配则说明检测出异常。
2 遗传算法
遗传算法(Genetic Algorithm,GA)是通过对生物系统进行计算机模拟演化而来的[4]。GA的理论依据来源于自然界生物进化机制,并在此基础上结合了达尔文进化论以及孟德尔遗传学说,是一种高效、并行、随机、全局的搜索和优化方法。遗传算法优化检测器的具体步骤为:
(1)对每条染色体所对应的个体适应度进行评价,把染色体比作检测器,每条染色体对应的个体适应度表示检测器对非自我元素的匹配程度。
(2)遵循适应度越高,选择概率越大的原则,即检测器与非自我元素的匹配度越高,该检测器成为成熟检测器的概率越大。
(3)从成熟检测器集中选择两个个体作为父方和母方,根据匹配度对父方、母方检测器进行交叉产生子代。
(4)对子代进行变异。
(5)判断检测器集中的检测器是否随着迭代次数的增加持续更新,当检测器停止更新或者达到迭代次数上限时输出结果,否则回到步骤(1)重新进行循环。
3 优化的阴性选择算法在齿轮箱故障检测中的应用
遗传算法优化的阴性选择算法在齿轮箱故障检测中应用的整体过程分为更新检测器和故障检测两个模块。在检测器更新阶段,先采集正常齿轮箱和故障齿轮箱的振动信号,处理正常振动信号后,根据阴性选择原理可以得到一个成熟检测器集。再用遗传算法优化已生成的成熟检测器,把每个检测器的故障检测率作为其优化适应度。假设进行了n次故障检测,对检测出的每个故障i(i=1,2,3,…,n),令Ai和Bi分别表示正常和故障状态下检测器可以匹配的样本数目。检测率Ci的表达式为:
4 仿真分析
常见的齿轮箱故障有断齿、磨损、点蚀等[5],本文主要对发生断齿和点蚀故障时的信号进行研究分析。为验证该方法的有效性,收集了5 000个正常齿轮箱的样本和5 000个故障齿轮箱的样本,故障类型分别为断齿和点蚀,断齿检测性能如图1所示。断齿和点蚀检测率如表1所示。为了对比效果,分别使用遗传算法优化后生成的检测器和未优化的阴性选择算法生成的检测器对两种故障进行检测。
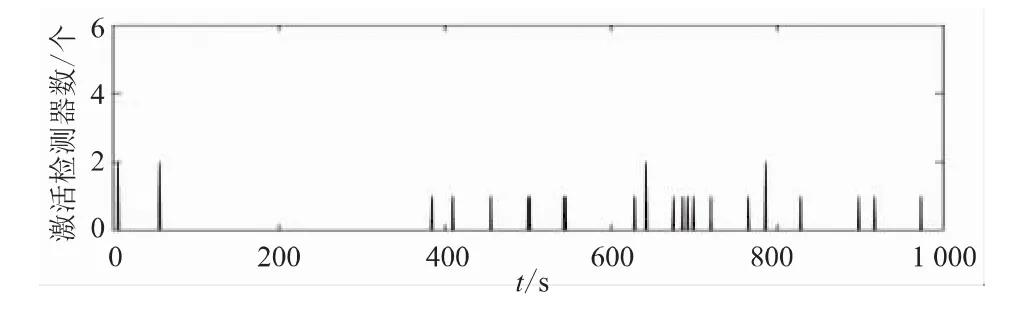
图1 断齿故障检测性能

表1 原始NSA检测器的故障检测率
用遗传算法优化后的NSA诊断断齿故障,其检测性能和检测率分别如图2和表2所示。
通过对比表1和表2的数据情况可以发现,普通检测器的C值仅为72.4%(A=8,B=21)使用遗传算法优化后C值增加到90%(A=12,B=106)。这表明通过遗传算法优化的阴性选择算法生成的检测器对单独的故障的检测率更高。
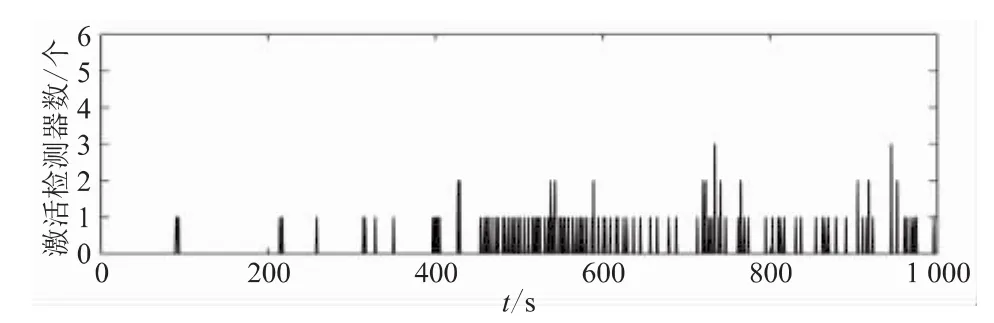
图2 遗传算法优化后的NSA检测器的断齿故障检测
以此类推,遗传算法优化后的检测器对具有双重故障(断齿和点蚀)的齿轮箱检测性能也有提高,检测率数据如表3所示。比较表1和表3即可发现,断齿和点蚀的检测率分别从72.4%和80%提高到88%和87.4%。由此可知,基于遗传算法优化的NSA对双重故障的检测率也有所提高。

表3 遗传算法优化的NSA检测器的双重故障检测率
5 结语
作为人工免疫系统典型算法之一,阴性选择算法在故障检测中得到了广泛的应用。本文提出了基于遗传算法优化的阴性选择算法,通过遗传算法优化NSA生成的成熟检测器,提升了故障检测效率。通过仿真分析得知,该方法可以有效提高单独故障及复合故障的检测率。

