基于多源数据的大范围无缝水下地形构建研究

蔡文婷

（鼎信信息科技有限责任公司，广东广州510623）

0 引言

在创新科技时代引领下，以高新技术为支撑的海洋战略将成为国家社会经济发展的战略要地[1]。“十二五”海洋科学和技术发展规划指出[2]：“海洋调查需步入常态化和全球化，海洋观测需进入立体观测时代，并向实时化、系统化、信息化、数字化方向发展。”近海大陆架蕴含丰富的油气、食物资源，优越的航运资源，是资源开发的战略性基地。以资源开发为目的的各类工程建设，例如滩涂养殖、能源开发、海岸防护、港湾建设、航道开发、电缆铺设等，都需要根据实际需求获取合适比例尺的水下地形。

传统船载声学测量往往基于测深设备并结合定位设备进行探深测量。首先，分析测区特点进行航线规划，生成合理的测深条带网并进行测量，再利用数据插值手段进行数据加密，从而得到测区水下地形，其测量精度高但量测范围有限[3-5]。随着航空、航天遥感技术发展，通过多分辨率、多成像方式的遥感影像反演水深已成为水深测量领域的新途径[6-9]。本文结合两种探测结果，取长补短，构建测区大范围水下地形数据。

1 研究区与数据预处理

1.1 研究区简介

本次数据获取依托南方电网海南联网路由检测工程。海南联网由中国南方电网责任有限公司投资建设，是国内第一个500 kV超高压、长距离、大容量的跨海联网工程。本次海底路由检测测区位于琼州海峡，海缆北侧登陆点在广东省湛江市徐闻县南岭村附近，南侧登陆点在海南省海口市澄迈县林诗岛附近的玉包角。以基于多源数据大范围无缝水下地形构建为目的，收集研究区多波束侧扫声纳数据用于精确表征测区水下地形，收集全球30"海底地形数据与30 m全球DEM数据用于与侧扫声纳数据融合构建适用于三维展示的大范围水下地形。具体收集的资料如表1所示。

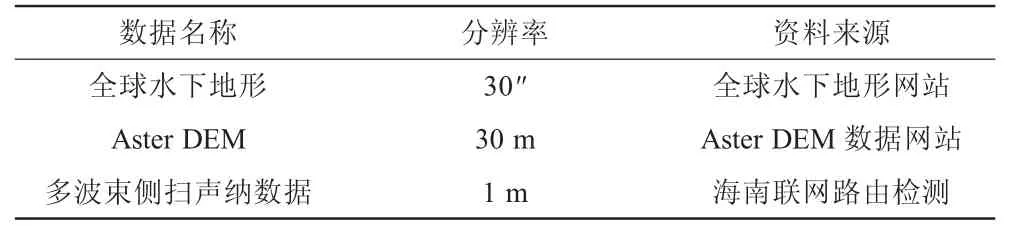
表1 研究区数据来源

1.2 数据预处理

考虑数据多源，为简化运算、提高结果可用性，分别针对声纳数据及遥感数据先进行有针对性的预处理工作。

1.2.1 全球水下地形数据

数据空间分辨率为30"，为提取水下地形数据，需遍历数据栅格选取数值小于0的数据并将计算结果转换为离散点。此外，还应剔除侧扫声纳数据所覆盖范围。

1.2.2 全球Aster DEM数据

数据空间分辨率30 m，不包含水下地形数据，可直接将数据转换为点数据。此外，由于数据空间分辨率高，可通过该数据提取海陆分界线，用于后续插值折断线需要。

1.2.3 测区多波束侧扫声纳数据

侧扫声纳数据空间分辨率为1 m，直接参与插值则会因离散点密度较大造成与30"水下地形数据交界处的内插结果出现锯齿状。

为消除锯齿现象，需对多波束侧扫声纳数据进行离散点抽稀工作，具体算法如下：（1）构建分区统计格网；（2）遍历格网内多波束点云，寻找最小值作为该格网中心水深值。

2 经验贝叶斯克里金插值

作为地质统计学的方法，克里金法已被广泛应用于地质学、水文学、土壤学等研究“时空变量”的数据处理领域，特别是在测深数据处理方面[10]。

普通克里金插值顾及了各观测点间的空间关系，可获得未知变量的最优线性无偏估计[11]，具有较高的估值计算精度。实际插值过程中，若存在异常数据，其变异函数会受异常值影响而偏离正确形状，进而降低插值结果精度。

本文引入一种经验贝叶斯克里金，实践证明，该方法具有较好的抗差能力。

2.1 普通克里金差值原理

假设在待估计点（x）的海域附近共有n个实测点，即x1，x2，…，xn，其样本水深值为Z（xi）。那么，普通克里金法的插值公式为：

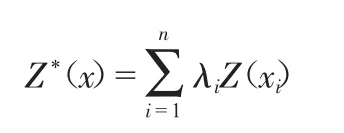
式中，λi为权重系数，表示各空间样本点xi处的水深观测值Z（xi）对估计值Z*（x）的贡献程度。

在引入变异函数的情况下，根据协方差与变异函数的关系γ（h）=c（0）-c（h），变异函数可等同于普通克里金方程组和克里金估计方差，即：

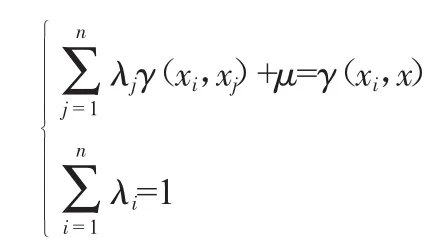
也可以将克立格方程组和估计方差用变异函数写成上述矩阵形式：

在具体求解中，如何有效获取变异函数的最优公式是克里金插值方法的关键，其主要受制于变异函数理论模型的选取和模型参数的估计。

2.1.1 样本变异函数值计算

由于数据分布不规则，为使较多的数据点参加计算，使求解出的样本变异函数值γ（dl）可信，应求解时取一常量Δd，寻找利用满足的已知水深点对，距离dl的变异函数样本值的求解公式为：

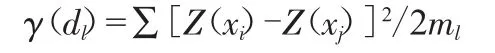
式中，ml为满足的点对数目。

2.1.2 变异函数理论模型的拟合

理论变异函数模型较多，常用的有指数、高斯、线性、对数、块金效应、幂函数、二次、推理二次、球状和孔穴效应、立方和五球形[12]。

由于理论变异函数模型比较多，一般利用残差、均方根预测误差以及相对均方差等指标来衡量评定各种模型的有效性。

2.2 经验贝叶斯克里金（EBK）

经验贝叶斯克里金法与普通克里金方法有所不同，它通过估计基础半变异函数来说明所引入的误差。普通克里金方法由于不考虑半变异函数估计的不确定性，因此低估了预测的标准误差。

经验贝叶斯克里金由于可准确预测一般程度上不稳定的数据，对于小型数据集，比其他克里金法更准确。此外，该模型可以用于插入非平稳数据，以至于可以在较大区域内，局部地将数据改造为高斯分布。

经验贝叶斯克里金法与普通克里金方法不同，它使用固有的0阶随机函数（IRF-0）作为克里金模型。

2.2.1 样本变异函数模型

对于给定距离h，经验贝叶斯克里金法使用以下形式的半变异函数：

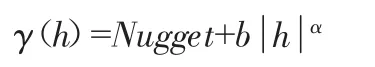
块金值和b（坡度）必须为正值，而α（幂）必须介于0.25和1.75之间。在EBK中，可以分析参数估计的经验分布，因为在每个位置都估计了多个半变异函数。

2.2.2 半变异函数估计

与其他克里金法不同，EBK中的半变异函数参数由受限最大似然法估计。计算过程中，可以按以下方式估计半变异函数：（1）通过半方差图模型对数据进行分析估计；（2）基于该半方差图，生产每个输入数据位置的新值；（3）使用新的模拟数据重新估计生成新的半方差图，最后根据这个半方差图的范围计算需要使用的贝叶斯经验规则。

3 实验结果及精度评价

为评价整体插值结果的优劣，本文根据以下四种方案评价本文所采用的技术路线的优势：

方案一：不进行任何点云抽稀，以海陆分界线为折断线，直接将所有数据参与运算；

方案二：对数据进行预处理工作，利用普通克里金方法进行插值；

方案三：选取已处理的数据，以海陆分界线为折断线，利用普通克里金插值；

方案四：选取已处理的数据，以海陆分界线为折断线，利用经验贝叶斯克里金插值。

各方案插值结果如图1所示。

图1 各方案插值结果示意图（相同配色方案）

从方案一插值结果可以看出，由于数据点云密度存在差异，多波束测量结果附近，由于搜索圆以最近距离为准则进行近邻点搜索，造成近邻点分布不均匀，插值结果存在明显条带阶跃性；同理，由于后续方案采取点抽稀，近邻点选取合理，插值结果过渡自然；从方案二配色方案可知，由于未利用海陆分界线作为折断线，造成海陆分界处待插值点的近邻点可能同时包含正负值，海陆分界错误。对比方案三、方案四，由于二者采取了点抽稀及折断线等优化方式，整体插值效果较好，但分析交叉验证结果可以发现，方案四的标准差较低，整体插值精度较高，如图2所示。

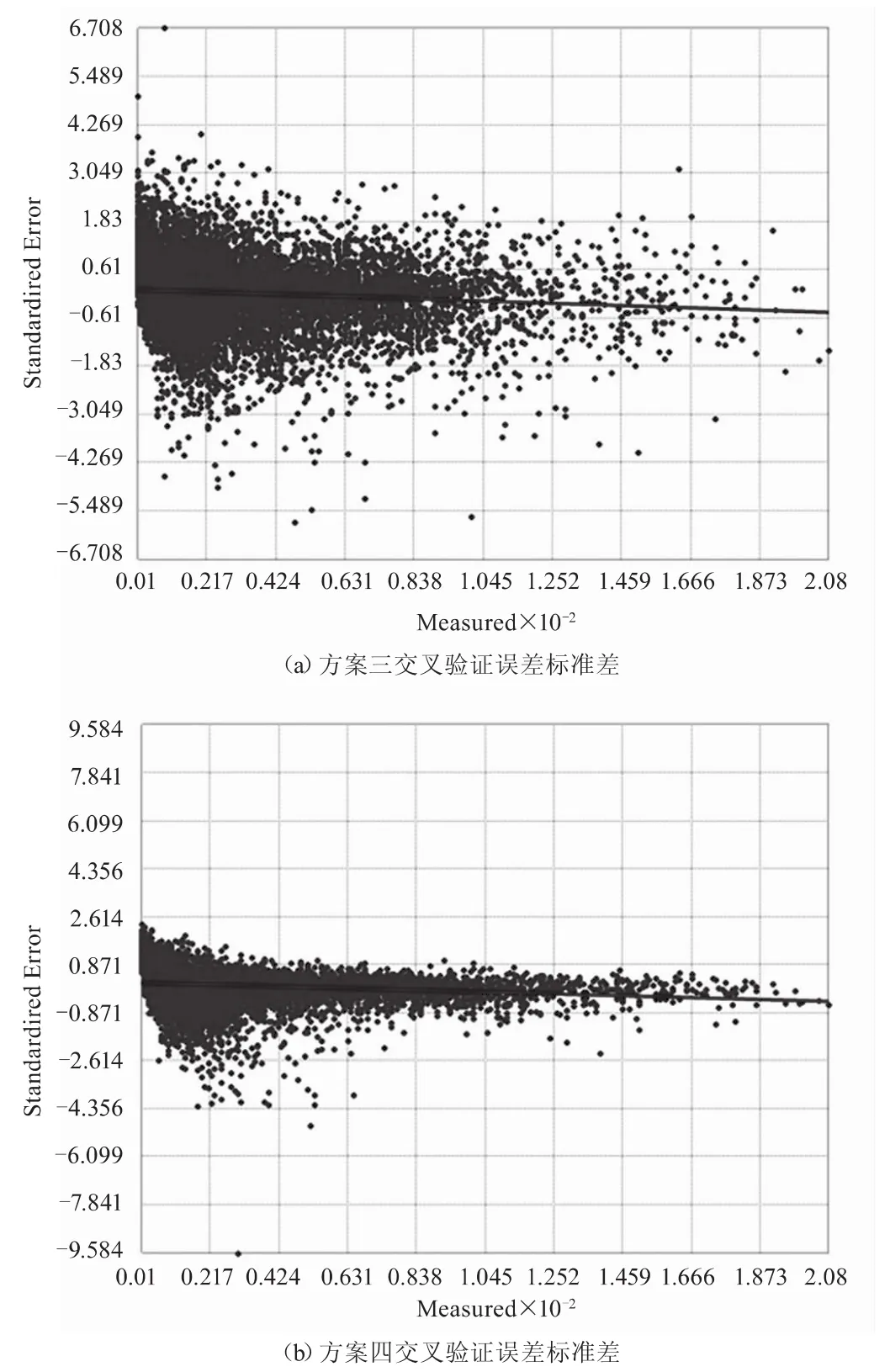
图2 两种克里金插值交叉验证误差标准差

4 结语

在现有测区多波束数据的基础上结合全球30"海底地形数据与30 m全球DEM数据为数据源，通过数据整理与抽稀、海岸线折断线以及经验贝叶斯克里金插值，构建覆盖测区的大范围的无缝地形的技术流程可靠：在进行数据插值时，已知点的密度和搜索圆共同决定插值点相邻点分布情况，在已知点的分布密度相差较大的情况下应进行相应的抽稀，以达到密度分布均匀的目的；涉及海陆分界的插值，为保证海岸线准确，应事先提取海岸线作为插值时的硬折断线。本文所介绍的经验贝叶斯克里金由于可准确预测一般程度上不稳定的数据，对于小型数据集，其插值结果比其他克里金法更准确。