ARIMA模型和灰色模型在农产品价格预测中的应用比较
丁慧娟,张金磊,陈建中,李均涛,崔 鹏
(贵州财经大学,贵州贵阳 550004)
农业一直是我国非常重视的问题,农产品供需是农业发展讨论的重要问题之一。2018年2月25日,“宣传贯彻中央一号文件精神暨2018中国三农发展大会”在北京召开,为推动大宗农产品贸易、预测和发现商品价格、引导农业产业结构调整、合理配置要素资源、维护农业发展稳定做出了积极贡献。受生产、流通、需求与供给等因素的影响,农产品日价格波动频繁。尤其近年来,受自然灾害、重大疫情等外部环境的影响,农产品价格波动频率有所增加。为此对农产品价格进行短期、中长期的预测,为农产品生产和流通提供重要的数据指导,对解决我国农产品供需问题、调整农业结构、促进市场经济持续健康发展具有重要的意义。
农产品的价格预测在国内出现比较晚,但发展快,预测方法多。刘峰等[1]运用ARIMA模型对白菜价格进行了预测,表明ARIMA(0,1,1)模型能很好地模拟并预测白菜月价格趋势。王素雅[2]对影响苹果价格因素做了分析,并通过构建价格时序模型对苹果旬价格、周价格、日价格进行了预测。徐雅卿等[3]运用指数平滑模型、ARIMA模型、组合预测模型对胡萝卜价格进行了预测,并提出了预测的改进方向。李干琼等[4]运用现代时间序列法建模对西红柿日批发价格进行预测,提出GARCH模型在预测中有更高的精度。任伟宏[5]介绍了现在预测方法中所涉及到的智能预测方法,分析了智能预测方法优于其他预测方法。姚霞等[6]通过构建平稳序列ARIMA自回归求平均模型,预测了时鲜农产品的价格。笔者采用ARIMA预测模型、灰色预测模型建模,对遵义猪肉进行月平均价格短期、中长期预测。
1 农产品价格模型构建
1.1ARIMA预测模型构建ARIMA预测模型中,预测值表示为最近的真实值和最近的预测误差组成的线形函数。ARIMA模型主要拟合具有平稳性的时间序列,非平稳性的序列可以通过差分转换为平稳性的序列。在一个p阶自回归模型中,ARIMA模型线形组合方程是[7]:
Yt=μ+φ1·Yt-1+φ2·Yt-2+…+φp·Yt-p+et
式中,Yt是时序任一观测值;μ是序列均值;φ是权重;et是随机扰动。在一个q阶移动平均模型中,残差线形组合方程是:
Yt=μ-φ1·et-1+φ2·et-2+…+φp·et-p+et
式中,e是预测的残差。一个ARIMA(p,d,q)过程是时序被差分d次,p个观测值和q个残差线形组合来表示。选择ARIMA模型的理论方法见表1。

表1 选择ARIMA模型方法
建立ARIMA模型的步骤如下:
(1)确保时间序列的平稳性。
(2)找出一个或者几个好的预测模型(即找出p值和q值可能存在的值)。
(3)拟合出所找模型。
(4)进行假设检验,对预测模型进行评估。
(5)对已经通过检验的模型进行预测。
1.2灰色预测模型构建灰色预测法是一种预测灰色预测系统的方法,对高阶系统建模,灰色理论是通过GM(1,1)模型群解决的。对该案例建立GM(1,1)模型如下:


(4)进行模型检测,灰色预测检验一般有残差检验、关联度检验和后验差检验。
(5)生成时序序列图,预测时序与原始时序进行对比。
2 农产品预测模型实验分析——以遵义肉价为例
2.1ARIMA模型实验分析
2.1.1数据稳定性检验。该研究选择遵义猪肉为预测对象,采用月平均价格,数据来源于贵州农金网遵义肉价日统计,经过加权计算作为遵义月平均价格数据。分析时间序列包括观测值、起始时间、终止时间及周期,只有将数据转换为时间序列对象后,如表2所示,才能用时间序列ARIMA模型进行分析、建模和绘图[8]。从图1可以看出,遵义猪肉的价格是随机的,有不稳定的特征,在2012年8月出现肉价最高,之后肉价处于下降趋势,总体猪肉价格处于上升趋势。

表2 时间序列数据
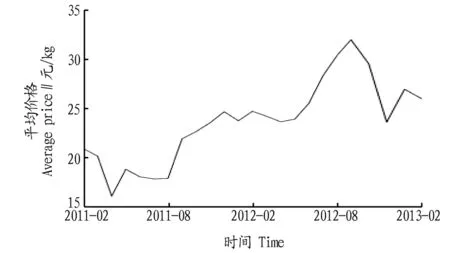
图1 遵义猪肉月平均价格时间序列Fig.1 Time series of pork monthly average price in Zunyi
运用R语言对遵义猪肉价格进行预测,通过diff()函数对序列进行差分,对猪肉价格时间序列图通过一次差分得到平稳序列图,通过adf.test()测试,测试结果如下:Dickey-Fuller=-2.829 7, Lag order=2,P=0.256 3。
若通过一次差分达不到时序平稳性,可以通过两次差分或多次差分,从测试结果P值可以看出测试值远远小于0.5,通过一次差分可以达到时序的平稳性。
2.1.2模型选择。通过ACF图和PACF图选择备选模型,运用Acf()函数和Pacf()函数生成序列ACF和PACF图,如图2、3所示,从前文中可以得出d=1,根据表1模型方法分析,从ACF图和PACF图中可以看出滞后阶数逐渐增加时,自相关逐渐减小至0,偏自相关逐渐减小至0,以此可以考虑ARIMA(1,1,0)模型。

图2 一次差分后的猪肉价格序列自相关图Fig.2 Autocorrelation diagram of pork price series after one difference

图3 一次差分后的猪肉价格序列偏自相关图Fig.3 Partial autocorrelation diagram of pork price series after one difference
2.1.3模型评价。对ARIMA模型进行拟合,模型拟合的好坏可以通过模型评价进行分析,如果拟合模型满足正态分布,数据中的点落在图中的线上,则表明拟合模型符合要求。拟合模型评价如图4所示,从图4可以看出所有的数据点几乎落在图中的线上,表明该例中结果非常好。再次通过 Box.test()进行测试,测试结果如下:X2= 0.006 292 1,df=1,P=0.936 8。
运用cat()函数获取残差值,如下所示:
绝对残差=(0.020 999,-0.757 042,-4.081 276,2.514 046,-0.619 662,-0.257 840,0.044 224,4.002 883,0.934 858,0.935 471,1.153 296,-0.861 772,0.912 523,-0.452 218,-0.584 501,0.229 803,1.596 763,2.856 936,2.203 293,1.718 465,-2.360 809, -6.015 747,3.027 720,-0.827 011,0.170 325)
相对残差=(0.000 999,0.037 400,0.251 931,0.132 851,0.034 117,0.014 369,0.002 457,0.181 949,0.041 134,0.039 597,0.046 632,0.036 190,0.036 836,0.018 632,0.024 650,0.009 587,0.062 485,0.100 848,0.072 504,0.053 702,0.079 877,0.254 187,0.112 138,0.031 808,0.006 495)
从测试的结果可以看出,模型的残差没有通过显著性检验,可以认为残差的自相关系数为0。ARIMA模型可以较好地模拟该数据。
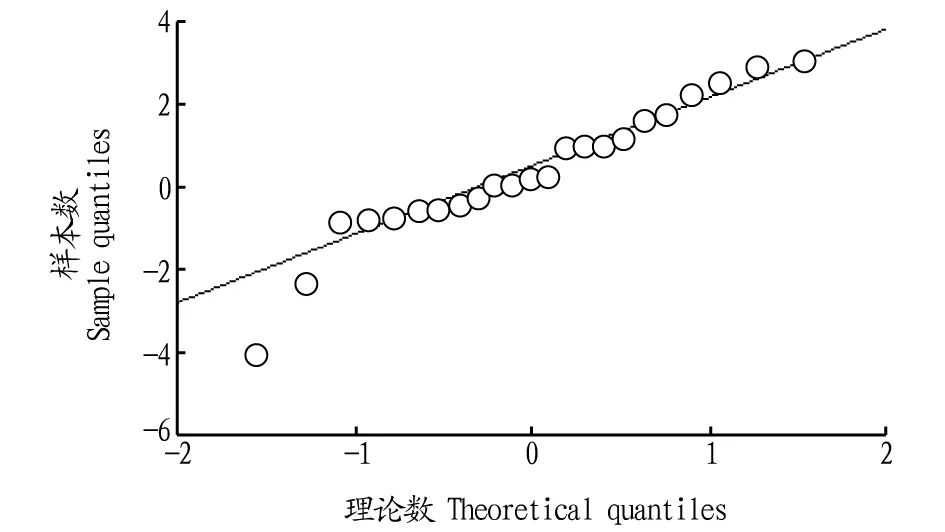
图4 正态Q-Q图Fig.4 Normal Q-Q diagram
2.1.4模型预测。接下来运用评价模型对猪肉价格进行预测,如图5所示,对未来的5个点进行了预测。图5中蓝色的点是点估计,浅蓝色区域和深蓝色区域分别代表80%的置信区间和95%的置信区间。预测结果见表3。

表3 ARIMA模型价格预测结果
从预测结果可以看出,猪肉价格未来5个月的平均价格基本处于稳定状态,没有很大的猪肉价格变动。在80%的置信区间和95%的置信区间预测出猪肉价格的最高价格和最低价格。
2.2灰色模型实验分析
2.2.1模型选择与检验。针对该例,选择的灰色预测模型为GM(1,1)模型,根据GM(1,1)模型建立的方法,建立R函数GM(1,1),运用cat()函数得出发展系数a和灰色作用量u,得出结果如下:发展系数a= 0.019 217 48,灰色作用量u=18.367 2。
然后求解方程,根据获得的a值和u值,得出预测模型。运用cat()函数获取模拟值,其中x(1)为拟合序列,x(0)为经后减运算还原所得模型输入序列预测序列,获取的模拟值如下:
x(1)=(21,39.952 29,59.272 32,78.967 22,99.044 27,119.510 9,140.374 6,161.643 2,183.324 4, 205.426 3,227.957 1,250.925,274.338 6,298.206 5,322.537 6,347.340 7,372.625 1,398.400 1,424.675 2,451.460 1,478.764 7,506.599 2,534.973 7,563.898 8,593.385 1,623.443 6,654.085 3,685.321 5,717.163 9,749.624 1)
x(0)=(21,18.952 29,19.320 03,19.694 90,20.077 05,20.466 61,20.863 73,21.268 55,21.681 24, 22.101 92,22.530 77,22.967 95,23.413 60,23.867 9,24.331 02,24.803 12,25.284 38,25.774 99,26.275 11, 26.784 93,27.304 65,27.834 45,28.374 53,28.925 09,29.486 33,30.058 46,30.641 7,31.236 25,31.842 34,32.460 18)
对获取的模拟值进行残差检验,运用cat()函数获取残差检验结果如下:
绝对残差=(0,1.289 649,-3.120 028,-0.771 090 7,-1.914 257,-2.522 169,-2.863 729,0.731 445,1.046 035,1.523 077,2.200 936,0.844 554,1.359 129,0.402 778,-0.618 789,-0.832 112,0.269 966,2.554 124,4.113 294,5.215 070,2.250 903,-4.167 778,-1.374 529,-2.925 089,-3.264 112)
相对残差=(0,0.063 712,0.192 594,0.040 747,0.105 395,0.140 554,0.159 096,0.033 248,0.046 026,0.064 469,0.088 992,0.035 467,0.054 86,0.016 595,0.026 096,0.034 713, 0.010 564,0.090 159,0.135 357,0.162 971,0.076 158,0.176 103,0.050 908,0.112 503,0.124 479)
从试验中获取:残差平方和=137.059 5;后验差比值检验c=0.340 925;小残差概率p= 0.96。
若后验差比值c<0.35,小残差概率p>0.95,模型为优;若后验差比值c<0.45,小残差概率p>0.80,模型为良;若后验差比值c<0.50,小残差概率p>0.70,模型为中;若后验差比值c<0.65,小残差概率p>0.70,模型为差。从上述的检验结果可以看出,c<0.35,p>0.95,GM(1,1)预测精度等级为优。
2.2.2模型预测。调用上述函数GM(1,1),运用plot()函数绘制出预测时序与原始时序对比图,如图6所示,从图中可以看出猪肉价格预测曲线总体处于上升趋势。

图6 猪肉价格时间序列Fig.6 Pork price time series
2.3模型对比研究为比较分析不同模型预测的精准性,通过上述实验得出平均相对误差和相对精度,结果见表4。
由表4可知,ARIMA模型比灰色模型的平均相对误差小约1.5%,ARIMA模型比灰色模型的相对精度大约1.5%,从平均相对误差和相对精度对比可以看出,ARIMA模型和灰色模型对猪肉价格的预测精准度相差不大,ARIMA模型略优于灰色模型。该试验的预测点为5个点,根据试验的预测结果图5和图6进行对比分析,ARIMA模型具有精准的点预测,预测价格在置信度为[80%,90%]区间内进行波动,GM(1,1)模型预测的是猪肉价格的未来走势,从图形走势可以看出猪肉的价格处于上升的趋势。再根据模型自身的特性进行对比分析,ARIMA模型在经济预测过程中既要考虑经济现象在时间序列上的依存性,又考虑了随机波动的干扰性,对经济运行短期趋势的预测准确率较高;灰色模型就是通过少量的、不完全的信息,建立灰色微分模型,对事物发展规律进行模糊性的长期描述。
表4不同模型误差和精度对比
Table4Comparisonofdifferentmodelerrorsandprecision%

3 结论
对遵义猪肉价格数据进行建模分析,只是做了初次的时间序列类似预测模型分析。从上述试验结果、预测图形以及模型特性对比分析可知,如果对猪肉的价格做出短期的精准预测,可以运用ARIMA模型进行短期预测,提高经济效益;如果对猪肉价格做出长期预测,可以运用GM(1,1)模型进行长期预测,使经济利益达到最大化。
农产品由于受各种因素的影响,农产品日价格波动频繁,为了稳定农产品价格,可以在此试验的基础上进行中长期的预测。可以进行进一步的研究,对该实验的灰色模型进行改进,运用不同数据处理方法对已有数据进行处理,提高预测精度,使预测的准确率更高、更可靠。

