动态同质网络上的SIR谣言传播模型
付 伟,王 静,潘晓中,刘亚州
(1.武警工程大学 密码工程学院,西安 710086; 2.西安高科技研究所 计算机科学与技术系,西安 710086)(*通信作者电子邮箱davidfuw@163.com)
0 引言
谣言,是指在社会中出现并流传的未经官方公开证实或已被官方所辟谣的信息[1-2]。互联网的快速发展为言论自由提供了良好的条件,同时也成为谣言产生和传播的重要媒介。与曾经口口相传的传统方式相比,互联网上的谣言具有更大的影响力,极易煽动群众引发群体性行为,危害社会稳定。为了更好地应对谣言扩散事件,降低谣言危害,研究新环境、新条件下的谣言传播机制依然是十分重要的课题。
从20世纪60年代起,科学家开始对谣言传播规律进行了研究。基于当时的科学技术,研究者发现谣言传播与流行病的传播存在诸多相似点,因此大量基于流行病传播模型的谣言传播模型纷纷建立。其中,Daley等[3-4]通过对谣言和流行病的传播机制进行分析研究,得到谣言传播不存在传播临界值,而流行病传播存在临界值,并且提出了封闭同质混合人群中的DK(Daley-Kendal)谣言传播模型。Maki和Thompson提出了MK(Maki-Thompson)模型[5],认为传播者与传播者接触时只有初始传播者会转变为免疫者。DK模型和MK模型为人们认识谣言传播规律提供了有效的理论指导。
随着WS(Watts-Strogatz)小世界网络模型[6]和BA(Barabási-Albert)无标度模型[7]的提出,复杂网络理论[8]得到了迅猛的发展,为研究网络传播动力学提供了理论基础,从此谣言传播研究进入到另一个新的阶段。2002年Zanette[9]利用复杂网络理论研究谣言传播,建立了基于小世界网络的谣言传播模型,证实均匀网络中存在传播临界值。随后,Moreno等[10-11]规范了谣言传播中的节点分类,并且研究了同质网络和异质网络下的谣言传播特性,指出在均匀网络下谣言传播不存在临界值。Zanette[9]和Moreno等[10-11]的研究成果奠定了复杂网络上谣言传播机制研究的基础,从最新的研究成果来看,众多的研究者依然遵循着这一研究方向。
Wang等[12]构建了一种新的SIR(Susceptible-Infective-Removal)模型,发现在延迟时间的影响下,节点识别力的存在略微降低了谣言传播程度,延迟时间越长,免疫策略的免疫效果越差。Jia等[13]重建了随机谣言传播模型,分析了谣言灭绝和持续的充分条件,获得了谣言持续存在与谣言灭绝之间的界限条件。Huo等[14]指出网络中每个节点按照一定的概率在高活跃状态和低活跃状态之间转动,引入了一个动态传播模型,利用Routh-Hurwitz准则得到了局部渐近稳定的平衡点。He等[15]基于异构网络的流行病模型,描述了MSN(Microsoft Service Network)中的谣言传播过程,提出实时优化和周期性地传播真相两种策略来抑制谣言传播。Liu等[16]考虑到暴露的节点可能以一定的概率成为被删除的节点,提出了一种新的SEIR(Susceptible-Exposed-Infective-Removal)谣言传播模型,并得到了谣言传播的阈值。Wang等[17]研究了两个媒介对谣言传播的影响,计算模型的均衡值,发现两种媒介之间的无知者的转化率直接影响着传播者的规模,不同的媒介对传播的动态行为有显着的影响。Wang等[18]研究了网络节点识别能力差异对谣言传播的影响,发现节点识别能力的差异延长了谣言传播到达稳定状态的时间,并减少了最终接受谣言的节点数量。
上述研究成果大都针对某一具体问题进行建模、论证,极大地丰富了谣言传播理论,为预测谣言提供了决策依据。值得注意的是,这些研究几乎都将系统视为一个稳定封闭的状态,将各类节点密度总和视为定值,并没有考虑传播过程中节点移出系统的情况。在现实传播过程中,谣言感染者在转变为谣言免疫者时,部分感染者可能会因传播谣言导致自身利益受损,选择离开整个系统。此时系统节点总数减少,虽然每一个时刻系统满足平衡条件,但是系统在不断地自我更新,为了研究非封闭系统中的谣言传播机制,本文结合复杂网络基本原理,提出动态同质网络上的SIR谣言传播模型。
1 谣言传播模型的建立
在经典SIR谣言传播模型中,网络中的公众状态分为三类:易感染者、感染者、免疫者。其中易感染者是指与谣言内容有一定联系且对谣言尚未知晓的公众;感染者是指认同谣言内容并传播谣言的公众;免疫者是指知晓谣言真相并不传播谣言的公众。SIR模型中s(t)、i(t)、r(t)分别表示三类节点t时刻在系统中的节点密度,并且满足s(t)+i(t)+r(t)=1,此模型较好地刻画了有限稳定状态下节点转换关系,进而分析得到谣言传播的一般机制。本文基于此模型的思想,考虑到存在节点移出系统的情况,系统由封闭状态变为非封闭状态,提出动态同质网络上的SIR谣言传播模型。为了不失一般性,本文将这类节点定义为移出者,即系统中部分节点知晓谣言真相并且直接离开系统。基于此划分规则,建立谣言传播模型如图1所示。

图1 动态同质网络SIR谣言传播模型
为了更好地研究谣言传播机制,本文考虑到现实生活中谣言传播存在的因果和接触两个特点,该模型提出以下3条假设以便进行数理分析和实验仿真。
1)如果易感染者与谣言传播者接触,则易感染者以α的概率成为谣言传播者,α称为谣言的感染率,其中0≤α≤1。从现实层面来看,一个谣言易感染者与一个谣言传播者接触后,该易感染者可能受谣言感染者影响,变为谣言感染者或者保持原先的易感染状态,所以模型以α刻画这种状态转变的可能性。
2)如果谣言感染者与另一个谣言感染者或者谣言免疫者接触,其自身将以概率β转变为谣言免疫者,β称为谣言的免疫率,其中0≤β≤1。从现实层面讲,一个感染者与另一个感染者或者免疫者接触,可能会产生“真相大白”的情况,其自身变为免疫者或者保持感染状态。
3)当发生2)中“真相大白”的情况后,在感染者转变为免疫者的过程中,部分传播者以概率1-μ离开系统,μ称为谣言感染者的真实免疫系数,其中0≤μ≤1。从现实层面讲,在“真相大白”后,部分感染者可能会因遭受重大损失而难以接受事实真相,选择直接离开系统。
该模型以s(t)、i(t)、r(t)分别表示谣言易感染者、谣言感染者及谣言免疫者t时刻在系统中的节点密度,N(t)表示t时刻系统节点相较于初始状态的实时密度值,移出者离开系统不作表示。
根据上文假设和传播规则,建立谣言传播模型平均场方程如下:
s′(t)=-α〈k〉s(t)i(t)
(1)
i′(t)=α〈k〉s(t)i(t)-β〈k〉i(t)[i(t)+r(t)]
(2)
r′(t)=μβ〈k〉i(t)[i(t)+r(t)]
(3)
N′(t)=-(1-μ)β〈k〉i(t)[i(t)+r(t)]
(4)
其中〈k〉为网络的平均度。上述平均场方程刻画了系统中各类节点密度变化的相互依赖关系。从整体看,方程组满足s′(t)+i′(t)+r′(t)=N′(t),系统处于动态平衡状态;从微观看,式(4)表明系统总节点数不断减少。
2 谣言传播过程的稳态分析
为了研究动态同质网络下的谣言传播机制,本章对传播动力学方程进行分析,构造了临界函数H(t),求解得到各类节点的稳定状态值s(∞)和r(∞),并得到感染峰值Imax,研究谣言传播达到稳态的条件。
2.1 临界函数
观察式(1)可知,s′(t)≤0,所以s(t)将不断减小,即易感染节点密度不断减小。同理,由式(2)可得,若N(t)/s(t)<α/β+1,则i′(t)>0,i(t)将不断增大,感染节点密度不断增大;若N(t)/s(t)>α/β+1,则i′(t)<0,i(t)将不断减小,感染节点数量不断减少。
为了便于下文讨论,构造谣言感染临界函数:
H(t)=N(t)/s(t)
(5)
易知H(0)=N(0)/s(0),则当H(t)>α/β+1时,即i′(t)<0,此条件下谣言不会扩散;当H(t)<α/β+1时,即i′(t)>0,此条件下谣言会扩散。
2.2 稳态分析
在谣言传播过程中,随着时间的推移,谣言的感染节点数量最终降低为0,易感染节点数量和免疫节点数量达到稳定状态不再变化。至此,谣言停止传播。
由式(1)、(2)、(3)、(4)得:
s(t)+i(t)+r(t)=N(t)
(6)
(7)
(8)
进一步可以得到:
(9)
令λ=β(1-μ)/α,化简得:
N′(t)s(t)-λs′(t)N(t)+λs′(t)s(t)=0
(10)
求解得N(t)与s(t)满足:
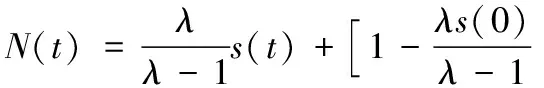
(11)
(12)
由式(6)、(12)可得:
(13)
联立式(11)、(12)、(13),可以得到:
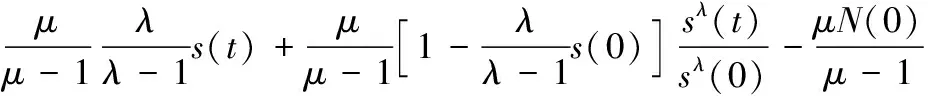
(14)
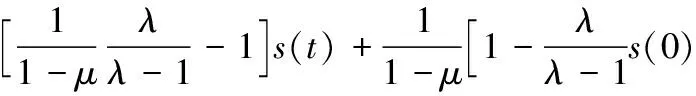
(15)
假设s(0)≈1,N(0)=1,由于i(∞)=0,结合式(11)、(14)、(15),得到稳态值s(∞),r(∞)分别满足:
sλ(∞)-(1+μλ-μ)s(∞)+μ(λ-1)=0
(16)

(17)
式(16)、(17)表明,谣言传播稳定状态依赖于μ、λ,在现实的谣言预测中,只需合理的估计谣言感染概率α、免疫概率β、真实免疫系数μ即可得到谣言传播过程的最终状态值,可为决策部门提供有效的参考。
2.3 谣言感染峰值
谣言感染峰值表示谣言传播过程中传播者数量的最大值,反映谣言在一次传播过程中的最大影响力,是分析谣言传播机制的重要指标。
由式(5)、(11)得:
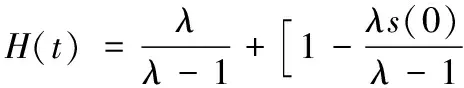
(18)
假设s(0)≈1,N(0)=1,对式(18)求导可得:
H′(t)=-sλ-2(t)s′(t)≥0
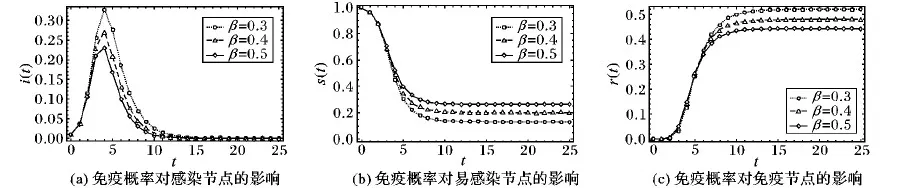
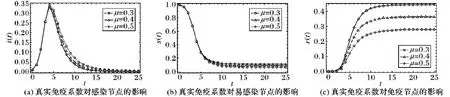
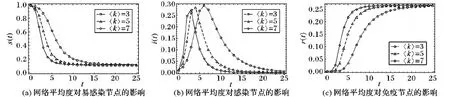
所以H(0) 由上述假设可得H(0)≈1<α/β+1,则存在时刻th使得H(th)=α/β+1,当0 在时刻th有H(th)=α/β+1,即: (19) (20) 为了得到感染峰值Imax,将s(th)代入式(15)中,可得th时刻感染节点密度: (21) 由式(21)可知,感染峰值Imax依赖于α、β和μ,与平均度〈k〉无关。 本实验是在Intel Core i5 2.6 GHz的主频,8 GB的内存,macOS的操作系统环境下,采用mathematica平台仿真。为了最大限度地模拟现实人群规模,仿真初始设为10 000,考虑到初始感染节点较少,假设s(0)=0.99,i(0)=0.01,r(0)=0,N(0)=1。为了不失一般性,尽可能地提高实验结果的适用范围,考虑到个体对谣言接受程度的差异性,本文设定不同的参数值。当i(t)=0时,谣言传播达到了稳定状态。 设模型中参数:α=0.4,β=0.6,μ=0.8,〈k〉=4.5,研究易感染节点、感染节点及免疫节点三类节点的密度随时间的变化情况。由图2可得,易感染节点密度s(t)在传播过程的初始阶段迅速下降,达到稳态s(∞)后不再变化,说明谣言在网络中传播较快且主要发生在前期。感染节点密度i(t)在传播开始后迅速达到感染峰值Imax,随后迅速降低为0。在传播过程的起始阶段,存在少量感染节点,易感染节点与之接触后以一定的概率转变为感染节点,i(t)增大。到达顶点后,易感染节点减少,免疫节点增多,感染节点减少。免疫节点密度r(t)在谣言传播开始后经过一段平缓期后迅速上升至稳定状态r(∞)。在谣言传播过程中,初期阶段免疫节点主要由感染节点相互接触转变而来,因此前期免疫节点较少。随着感染节点的增多,免疫节点迅速增多。当感染节点密度i(t)降为0时到达稳定状态。由于存在节点移出系统,所以相较于原始系统,节点密度n(t)出现了降低,到达稳态后不再改变。 图2 各类节点密度随时间的变化 设模型中参数:α=0.2,β=0.3,μ=0.3,〈k〉=4.5,分别对两种模型中易感染节点、感染节点及免疫节点三类节点的密度随时间的变化情况作了对比研究。 由图3(a)可得,易感染节点数量在两种模型下先减小,达到稳态s(∞)后不再变化。区别在于,在经过一段时间的同步后,考虑节点移出的SIR模型中易感染节点数量s1(t)下降幅度较SIR模型中的易感染节点数量s2(t)下降幅度大。 由图3(b)可得,感染节点数量在两种模型下均是先增加,达到峰值后迅速下降,最终为0。在传播过程前期,两种模型下的感染节点变化趋势经历了一段时间的同步。不同之处在于,考虑节点移出的SIR模型的峰值比SIR模型的峰值大,到达峰值的时间比SIR模型达到峰值的时间稍有推迟。 由图3(c)可得,免疫节点数量在两种模型下均是先经历一段时间的“平静期”,而后迅速增大,最终达到稳态r(∞)不再变化。区别在于,相较于SIR模型中免疫节点的变化,在经历了“平静期”后,考虑节点移出的SIR模型免疫节点数量增幅较小,增较小,稳态值较小。在谣言传播过程中,感染节点移出对免疫节点变化具有较大的影响。 通过对比分析可以得到,在谣言的传播过程中,由于部分传谣的人利益受到损失而选择直接离开整个网络,相较于原始网络,易感染节点密度出现一定幅度的下降,免疫节点密度下降幅度较大,感染节点密度出现一定的增大。尽管出现了这些差别,但是两种模型前各类节点变化趋势大致相同。 3.3.1 感染概率对谣言传播过程的影响 设模型中参数分别为:β=0.4,μ=0.3,〈k〉=4.5,在各类谣言中,感染率高的谣言意味着更能吸引公众的关注,更容易传播。图4分别表示为不同感染概率下易感染节点、感染节点以及免疫节点的密度随时间变化关系图。由图4(a)可得,随着感染概率的增大,感染过程的速度变化得更快,感染峰值Imax更大,到达峰值Imax的时间也越早。图4(b)表示感染密度对易感染节点密度的影响。由图可知,随着感染概率的增大,易感染节点密度下降越快,稳态定状态值s(∞)越小。由图4(c)可得,随着感染概率的增大,免疫节点密度增大越快,稳态值越大,到达稳态的时间相对提前。 图3 三种类型的节点密度随时间的变化对比 图4 感染概率对节点密度的影响 3.3.2 免疫概率对谣言传播过程的影响 设模型中参数分别为:α=0.3,μ=0.6,〈k〉=4.5,图5分别表示为不同免疫概率下感染节点、易感染节点以及免疫节点的密度随时间变化关系。从整体上看,虽然免疫概率不同,但三种节点的密度变化曲线在前期出现重合,表明免疫概率对谣言传播过程的前期几乎没有影响。随着传播过程的发展,免疫概率对传播过程的影响逐渐凸显。具体表现是,免疫概率越大,感染峰值越小,到达峰值的时间相同,节点密度下降得越快;免疫概率越大,易感染节点密度下降得越慢,稳态值越大;免疫概率越大,免疫节点密度上升越快,稳态值越小。 3.3.3 真实免疫系数对谣言传播过程的影响 在谣言传播过程中,由于利益的损失,感染者转变为免疫者的过程中,部分感染者以概率1-μ离开系统。为了研究这种因素对谣言传播的影响,设模型中参数为:α=0.3,β=0.3,〈k〉=4.5。图6分别表示不同真实免疫系数下易感染节点、感染节点以及免疫节点的密度随时间变化的关系。从整体上看,三幅图像中的曲线在前期均有一段重合,当达到感染峰值后出现轻微区别,对易感染节点的稳态影响不大,对免疫节点的稳态影响较大且影响程度较为均匀,真实免疫系数越大,免疫节点稳态值越大。 网络平均度是社交网络拓扑结构的重要特征参数,它表示网络中每个节点与周围节点的平均连接数目。为了研究一般性规律,不针对具体网络结构,通过抽象出节点平均度,研究节点移出的SIR模型中网络平均度对谣言传播过程的影响。设模型中参数分别为:α=0.3,β=0.4,μ=0.3,将平均度〈k〉分别设置为3、5和7,进行仿真计算如图7所示。 图7表示不同网络平均度下的各类节点密度随时间变化的关系图。由图7(a)可得,网络平均度越大,易感染节点密度下降得越快,到达稳定状态越早,稳态值一致;由图7(b)可得,网络节点平均度越大,感染节点密度增加得越快,到达峰值的时间越早,下降得也越快;由图7(c)可知,平均度也越大,免疫节点密度上升越快,到达稳态时间越早,稳态值一致。仿真结果表明,网络平均度对谣言的传播过程具有重要影响,但没有改变稳定状态值。 图5 免疫概率对节点密度的影响 图6 真实免疫系数对节点密度的影响 图7 网络平均度对节点密度的影响 本文针对节点移出网络的情况,提出动态同质网络上的SIR谣言传播模型,解决了系统动态变化中的谣言传播问题,拓展了SIR谣言传播模型的应用范围。研究表明,动态同质网络上的SIR谣言传播模型存在理论上的感染峰值和传播稳态,参数对谣言传播过程的影响各有侧重。考虑到移出节点的度不同,动态非均匀网络上的SIR谣言传播模型是否依然存在感染峰值和稳态是一个研究难题。
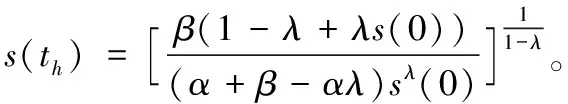
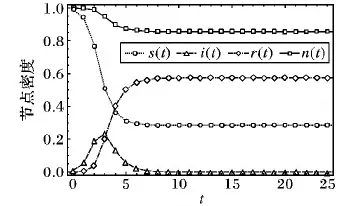
3 数值仿真及分析
3.1 考虑节点移出的SIR模型中各类节点密度随时间变化
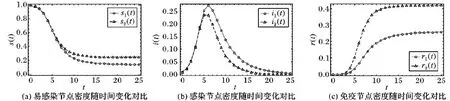
3.2 节点移出的SIR模型与SIR模型中各类节点密度对比
3.3 感染率、免疫率及真实免疫系数对谣言传播阈值的影响
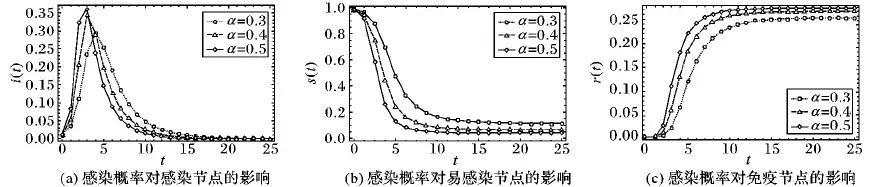
3.4 网络平均度对谣言传播过程的影响
4 结语

