光测站点垂线偏差对飞行器定位的影响分析*
牟志华,聂 凯,栾瑞鹏
(92124部队,辽宁大连 116000)
0 引言
光学测量系统(简称光测)是飞行器试验初始段和再入段的主要测量系统之一,不但直观性强、定位精度高,而且测量稳定可靠,不受“黑障区”和地面杂波干扰[1]。光测数据处理主要是分析利用多台光测设备的测量数据,解算出飞行器的运动轨迹参数,作为飞行器试验技术性能和指标评定的重要依据。以往的光测数据处理,虽然没有考虑站点垂线偏差的影响,处理精度也能满足测控需求。随着外场硬件设备测量精度的不断提高,为使测量数据发挥最大作用,要考虑各种微小误差对数据处理结果的影响,垂线偏差是一个容易被忽略的小量,要得到高精度的飞行器轨迹参数,深入分析和研究光测站点垂线偏差对定位结果的影响十分必要。
文献[2]用飞行器理论轨迹仿真了惯导地平系轨迹数据,定量分析了垂线偏差对数据处理精度的影响;文献[3]研究了存在垂线偏差条件下惯性制导初始方位角出现误差的机理,给出了垂线偏差所造成的初始方位角误差的修正公式;文献[4]建立了惯导系统速度、位置的误差方程,采用了三种分辨率的重力网格数据对垂线偏差进行插值补偿。在测量和数据处理领域,高精度的硬件设备要求高精度的数据处理方法,文中从设备的测量原理作为切入点,对测量数据进行分析,依据坐标系旋转和矩阵变换理论,推导了站点垂线偏差对方位角和俯仰角的影响公式,仿真计算出对多站最小二乘交会定位结果的影响。
1 大地测量中的垂线偏差
地球是一个非均质椭球体,地面或空间一点P的铅垂线和法线一般是不重合的,铅垂线与该点对参考椭球面法线之间的夹角,称为该点的垂线偏差,如图1所示。垂线偏差反映了大地坐标与天文坐标之间的差异和关系,可以通过天文坐标、大地坐标或重力测量资料计算求得[5]。在数据处理中,一般将垂线偏差在子午面上的分量称为子午分量或南北分量,记作ξ,约定取向北为正;在卯酉面上的分量称为卯酉分量或东西分量,记作η,约定取向东为正。垂线偏差与椭球的定位有关,对于同一点而言,基于不同椭球体建立不同大地坐标系,有不同的垂线偏差分量[6]。

图1 空间某点垂线偏差示意图
设某点P的天文坐标为(λ,φ,h),大地坐标为(L,B,H),该点垂线偏差计算公式为:

(1)
2 光测站点垂线偏差对定位影响
在光学测量系统中,测站是在测量坐标系(站心系)下对飞行器的方位角和俯仰角进行测量,光学测量系统的两个角度测量值与水平面有关,属垂线测量坐标系,在进行数据处理时,要考虑垂线测量坐标系到法线测量坐标系的转换问题。
2.1 坐标系定义及转换关系
垂线测量坐标系:原点K定义为光测设备三轴交会中心;KX轴定义为在过原点K的水平面内,指向当地的天文北方向;KY轴定义为过K点的铅垂线,向上为正;KZ轴定义为在过K点的水平面内,与KX、KY轴构成右手直角坐标系。
法线测量坐标系:原点K定义为光测设备三轴交会中心;KX′轴定义为在过原点K的椭球体切平面内,指向当地的大地北方向;KY′轴定义为与过K点的椭球体的法线重合,向上为正;KZ′轴定义为在过K点的切平面内,与KX′、KY′轴构成右手直角坐标系[7]。
假设某光测站点坐标原点K的大地坐标为(LK,BK,HK),天文坐标为(λK,φK,hK),垂线偏差子午分量为ξK,卯酉分量为ηK。对于同一光测站点,垂线测量坐标系与法线测量坐标系的原点相同,都是基于原点K,法线测量坐标系K-X′Y′Z′绕KZ′轴顺时针旋转ξK角,再绕KX′逆时针旋转ηK角,再绕KY′轴旋转γK角,得到垂线测量坐标系K-XYZ。坐标旋转关系示意图如图2所示。
假设目标M在垂线测量坐标下的坐标为(x,y,z),在法线测量坐标系下的坐标为(x′,y′,z′),两者之间转换满足如下关系式:
(x,y,z)T=ΩK(x′,y′,z′)T
(2)
ΩK=[MγK][MηK][MξK]
(3)
(4)
(5)
(6)
γK=arcsin[sin(λK-LK)sinφK]
(7)
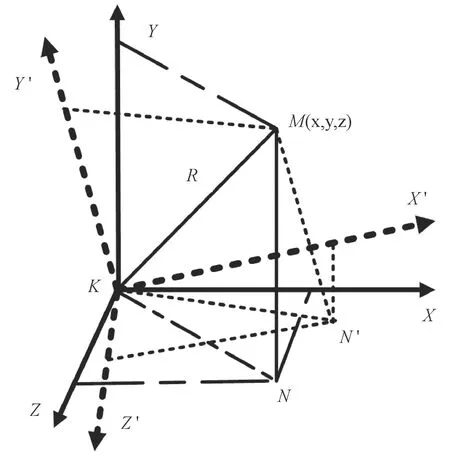
图2 垂线与法线测量坐标系关系示意图
2.2 垂线偏差对角度测量值的影响
已知某光测站点测量某空间目标点M的测量值方位角为A,俯仰角为E,该测量值是基于垂线测量坐标系的,在交会计算时,转化为法线测量系下的测量值,设方位角为A′,俯仰角为E′。该目标点M到测站测量原点的斜距R是一样的,目标定位用几何方法表示为:
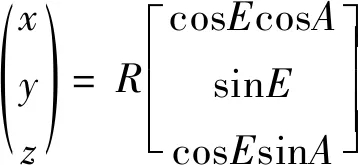
(8)

(9)
由坐标旋转变换矩阵的可逆和正交条件[8],有:
(10)
为表述方便,假设:
(11)
可推导法线测量系下的测量值为:
A′=arctan(K1/K2)
(12)
E′=arcsin(P12cosEcosA+P22sinE+P32cosEsinA)
(13)
K1=P13cosEcosA+P23sinE+P33cosEsinA
(14)
K2=P11cosEcosA+P21sinE+P31cosEsinA
(15)
将垂线测量坐标系下测量值与法线测量坐标系下推算值作差,定义垂线偏差在方位角和俯仰角上带来的误差影响值为:
ΔA=A-A′,ΔE=E-E′
(16)
2.3 垂线偏差对定位结果的影响
在实际试验中,光测站点的测量参数是方位角A和俯仰角E,所求参数为发射系下的坐标,观测数据与待估参数间呈非线性关系,在进行光测多台最小二乘交会估计时,要对非线性模型进行线性化处理,设非线性模型用矩阵形式表示如下:
Y=f(βT)+e
(17)

(18)
最小二乘交会估计[9]公式为:
(19)
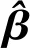
(20)
采用迭代计算方法可以获取精确的估计结果。
对于目标点M而言,采用上述最小二乘估计,得到垂线测量系的测量值在发射系下交会结果为(x,y,z),经转换到法线测量系的测量值在发射系下的交会结果为(x′,y′,z′),由站点垂线偏差带来的交会坐标差值为:
Δx=x-x′,Δy=y-y′,Δz=z-z′
(21)
由站点垂线偏差带来的交会点距离差定义为:
(22)
3 仿真算例
选取5个光测站点,利用仿真数据生成垂线测量系下的测量数据方位角Ai和俯仰角Ei,表1给出了测站垂线偏差的子午分量和卯酉分量。

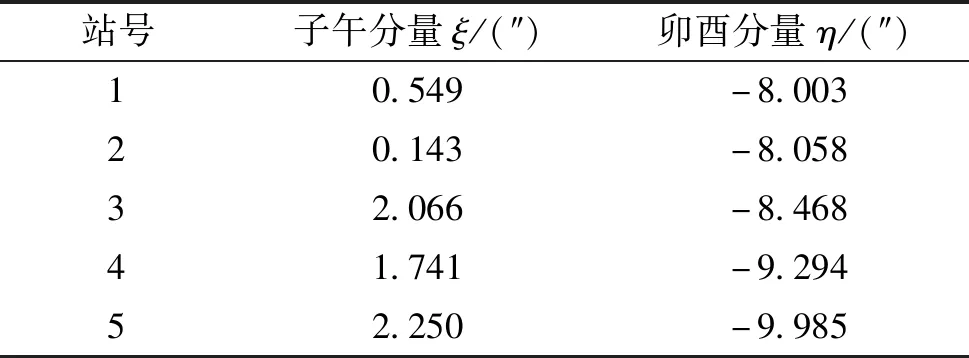
表1 测站垂线偏差分量表

表2 垂线偏差对方位角影响最大值
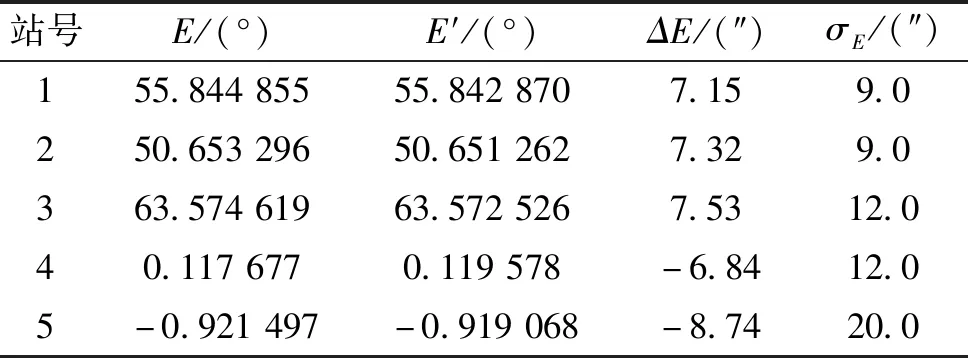
表3 垂线偏差对俯仰角影响最大值
表2中A表示垂线测量系下方位角测量值,A′表示法线测量系下方位角推算值,ΔA表示垂线偏差对方位角的影响最大值,σA表示站点设备方位角测量精度值。表3中E表示垂线测量系下俯仰角测量值,E′表示法线测量系下俯仰角推算值,ΔE表示垂线偏差对俯仰角的影响最大值,σE表示站点设备俯仰角测量精度值。
选取3号站点的仿真数据,绘制垂线偏差对方位角和俯仰角的影响差值曲线如图3和图4。从图3看出,在某些时间段,站点垂线偏差带来的方位角误差达到-28″,远远超过了测量设备的测角精度12″,也就是最大值超过设备测量精度的2倍,从图4看出,垂线偏差带来的俯仰角误差在-8″和8″之间变化,最大值也超过了设备本身的测量精度的50%以上。

图3 垂线偏差对方位角的影响
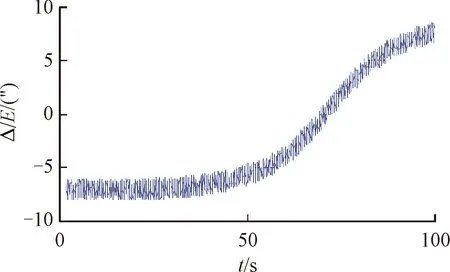
图4 垂线偏差对俯仰角的影响
将各光测站带有垂线偏差的测量数据和修正垂线偏差的测量数据分别采用式(17)~式(20)进行最小二乘多台交会,得到两组数据,即包含站点垂线偏差的坐标和修正站点垂线偏差的坐标。采用式(21)将两组数据作差,可以得出在当前布站情况下,光测站点垂线偏差对定位结果的分量影响。绘制差值曲线如图5、图6、图7所示。采用式(22),计算站点垂线偏差带来的交会点距离差,绘制曲线如图8所示。
从图5~图7看出,站点垂线偏差对定位x方向的影响随时间的增加而线性增大,最大值在100 s时,超过2.6 m;对y方向的影响最初表现不明显,在70 s以后迅速增大,在100 s时,达到-1 m;对z方向的影响较小,在75 s最大值不超过-0.3 m。从图8看出,垂线偏差对交会点距离差的影响,随时间增加而增大,在100 s时接近3 m。

图5 垂线偏差对定位x方向的影响

图6 垂线偏差对定位y方向的影响

图7 垂线偏差对定位z方向的影响

图8 垂线偏差带来的交汇点距离差Δr的变化
综上,光测站点垂线偏差对设备测量的方位角和俯仰角影响较大,进而影响事后精细数据处理精度。以上算例中,采用的仅仅是正常范围内的垂线偏差数据,子午分量ξ的值在2.3″以内,卯酉分量η的值在-10″以内,都不是极端情况。垂线偏差是由于地球地表形状不规则,地球内部质量分布不均匀等地理自然因素引起的实际重力方向与该位置点正常重力的小角度偏差,在某些山区和大山区等地形复杂的地方,垂线偏差变化剧烈,可达20~30″[10],所以光测数据精细处理中,必须考虑对测站垂线偏差进行修正。
4 结论
文中针对光测站点,推导了垂线偏差对方位角和俯仰角的影响公式,进而推导出对多站最小二乘交会定位结果的影响。通过仿真计算,得出在某种特定布站情况下,光测站点垂线偏差对方位角的影响最大值超过设备的方位角测量精度值2倍,对俯仰角的影响最大值超过设备的俯仰角测量精度值的50%,垂线偏差对定位结果的影响,主要表现在x方向和y方向上。在飞行器试验的事后数据处理中,基于垂线测量坐标系下的测量设备都存在垂线偏差修正问题,为了与外场硬件设备的测量精度提升相适应,使测量数据发挥最大作用,提高数据处理精度,对站点垂线偏差进行修正十分必要。

