Morison模型在半潜式平台方案设计中的应用

，，，

(1.中集海洋工程研究院有限公司，山东 烟台 264000；2.烟台中集来福士海洋工程有限公司，山东 烟台 264000)

在半潜式平台方案及概念设计阶段，为了获取更好的平台总体性能，往往需要进行大量计算分析工作，对方案进行优化设计。虽然计算机硬件及分析软件不断快速发展，使得单个方案的水动力性能分析时间大幅缩减，但是目前单个方案的基于面元模型的水动力分析建模、水动力系数计算及相关计算结果的后处理一般仍需要1-2 h的工作时间。因而，如果设计过程中进行大量方案的比对工作，仍需耗费大量分析时间。在项目设计周期一定的情况下，大量的计算时间已经成为制约平台获取优化设计的瓶颈。Morison模型作为早期半潜式平台水动力分析广泛使用的方法之一，随着计算机软件及硬件的发展，目前单独使用较少，但其计算效率及获取平台运动性能变化特性方面仍然具备良好的应用基础[1-2]。因此，考虑对Morison模型进行改善，缩短多方案性能计算时间。通过Morison模型进行大量方案的比选计算，最终对优选出的方案再进行详细的面元模型建立、计算及结果评估。

1 理论基础

在半潜式平台运动性能分析中主要有2种分析方法：①基于细长体理论的Morison模型，②基于势流理论的面元模型，有时会结合Morison和面元模型的优点联合使用。

1.1 Morison模型

Morison模型主要将半潜式平台主要构件，如浮筒、立柱和横撑等假设为细长杆结构，在进行波浪力计算时通过拖曳力系数和惯性力系数及杆件相对于波浪流体质点速度和加速度进行的简化受力计算，进而获取相关平台水动力性能。Morison受力公式如下[3]。

(1)

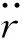
1.2 面元模型

面元模型主要是采用面元网格对浮体表面进行离散，在面元上均匀分布源汇强度，采用源汇表征流场速度势的分布。通过求解源汇强度，获得平台在单位波幅波浪作用下的频域运动响应算子(RAO)。面元模型的基本假设是流体为无粘、无旋的理想流体，在流体域中速度势满足拉普拉斯方程，在壁面处满足不可穿透条件，满足远方无辐射条件等[4]63，[5-7]。

1.3 运动方程求解

浮体线性运动方程为[4]66

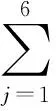
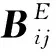
1.4 Morison模型的改进

目前商业软件[4]中Morison模型一般都简化成圆柱形杆件，赋予不同方向的阻力系数和惯性力系数来模拟实际平台的浮体结构。由于刚度矩阵等信息还是通过圆柱形杆件获取，因而刚度矩阵上与实际平台不符。因而，往往需要根据实际平台尺度计算出相应计算工况下的刚度矩阵，然后输入到计算模型中，再进行相关计算。

同时，在使用Morison模型计算时，半潜平台浮筒和立柱结构形式多为矩形带倒圆角结构，阻力系数可以参考DNVGL-RP-C205。但是附加质量系数目没有找到合适的参考资料。

针对上述的局限性，通过自编基于Morison理论的平台运动分析的计算程序。将半潜式平台简化成带倒角的矩形截面，进行相关静水力参数计算，获得准确的浮力及刚度矩阵。同时，引入CFD技术[8-9]，计算典型剖面的附加质量系数，作为输入参考。参考文献[8]中采用CFX软件进行附加质量系数计算，本文采用Star CCM+软件进行二维截面附件质量系数计算。总体的计算思路为给静止在流体域中的物体一个很小的加速度，使物体做匀加速运动，监控一个时间步长内的物体受力，此时物体速度很小，粘性力可以忽略，物体在运动方向上的受力即为物体所受的惯性力，再除以物体的运动加速度，即可得到物体的附加质量。典型附加质量计算流场见图1。通过该方法进行不同长宽比及倒角半径的几何形状的附加质量系数，作为Morison模型的输入参数。

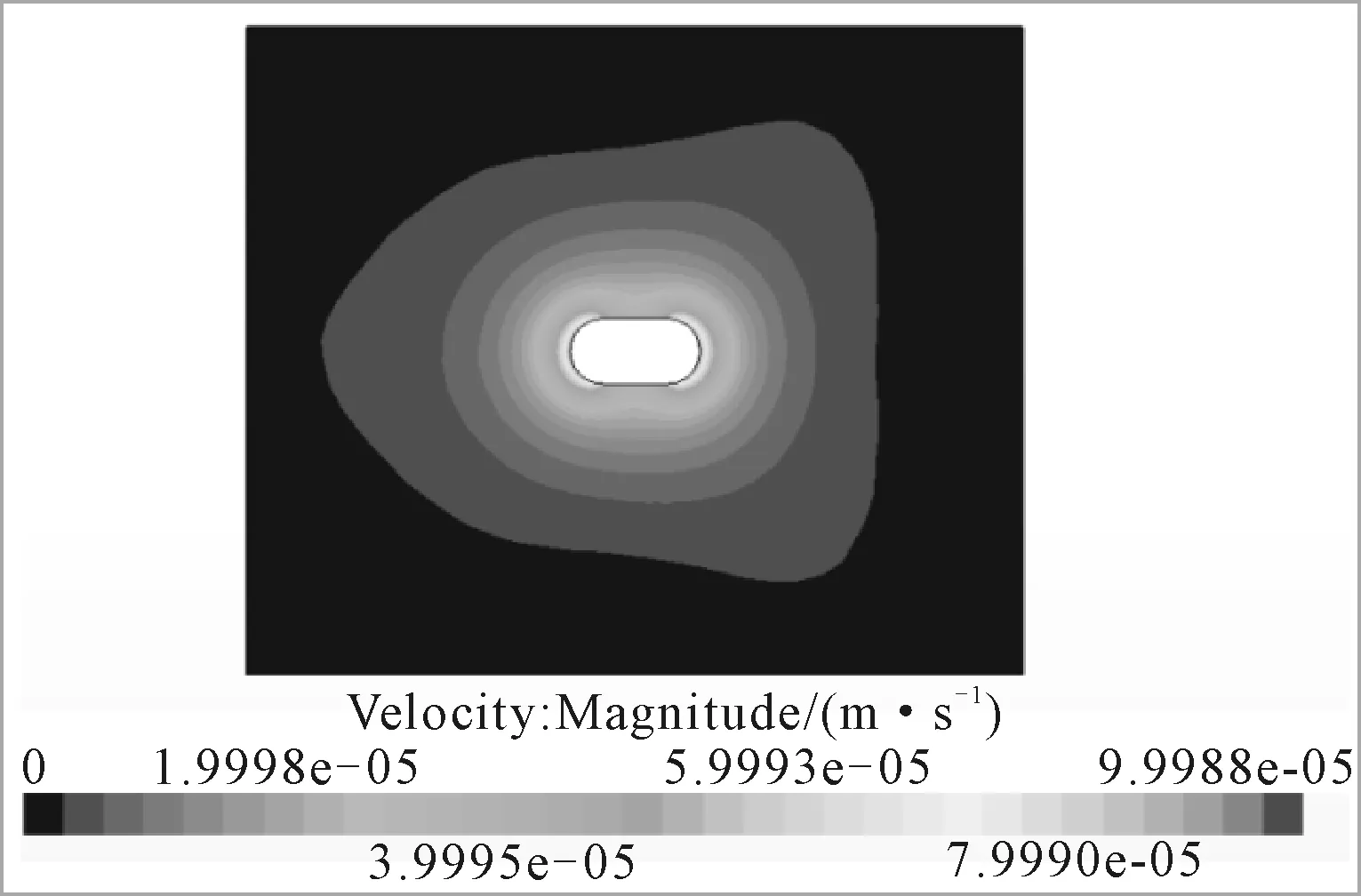
图1 附加质量计算流场示意

2 算例分析

2.1 自编程序结果可靠性验证

为验证自编程序与商用软件的计算精度，进行相关算例验算工作。对比软件采用SESAM/HydroD。分析模型信息如表1中方案3相关数据。面元计算模型见图2。

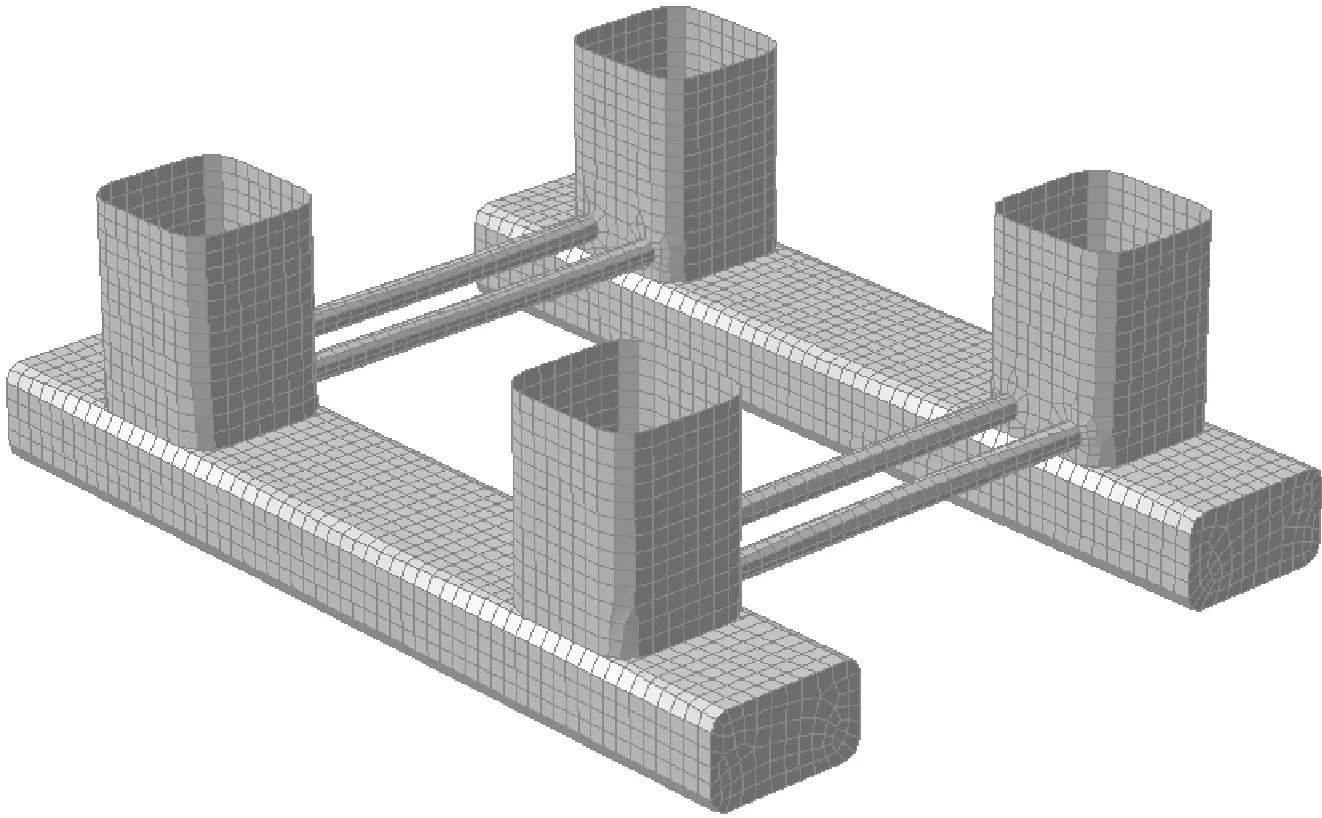
图2 水动力分析面元模型

一般在半潜式平台设计过程中，比较关注垂荡响应、横摇响应和纵摇响应[10-12]，计算结果(图3～5)表明，自编程序与商用软件分析程序的计算结果完全一致。

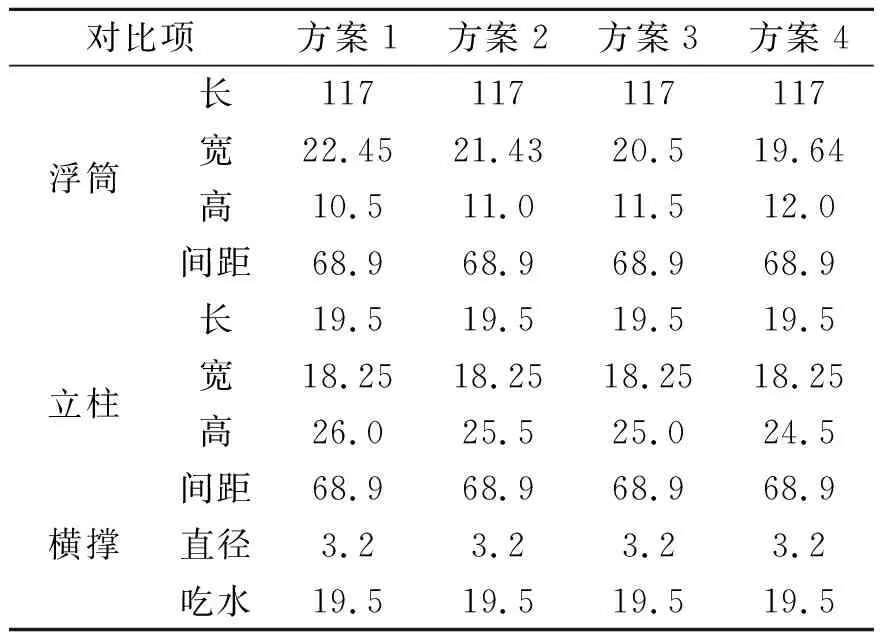
表1 对比分析模型主要信息 m

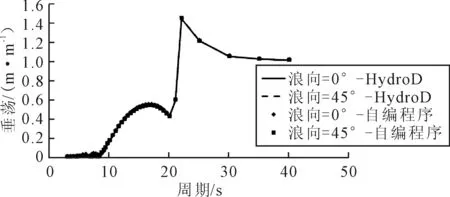
图3 垂荡响应RAO对比

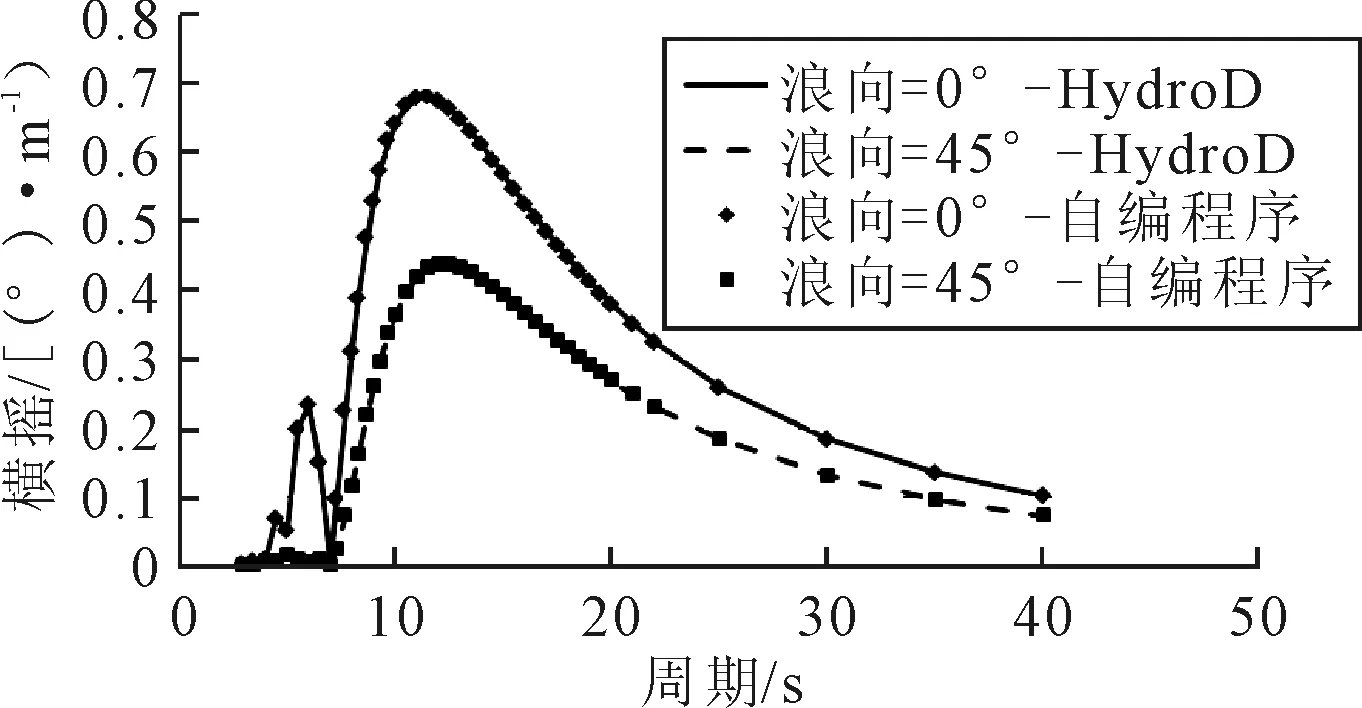
图4 横摇响应RAO对比

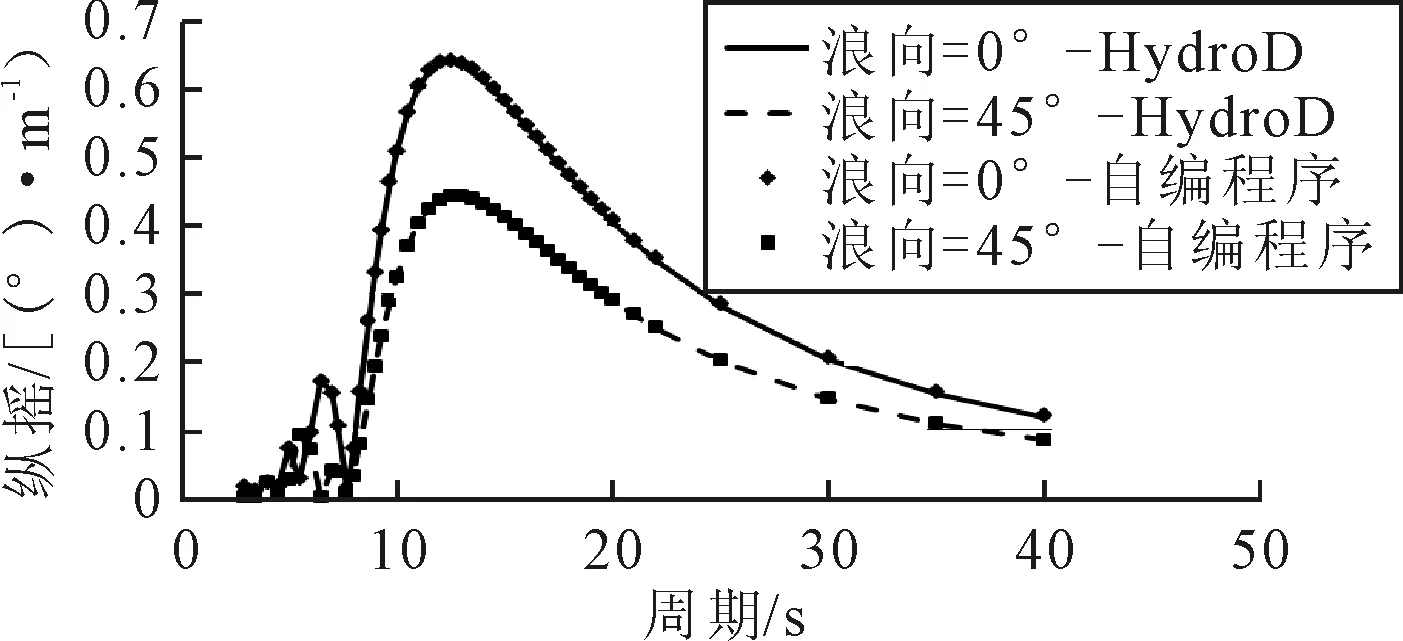
图5 纵摇响应RAO对比

2.2 Morison与面元模型计算结果对比

为了论证Morison在半潜式平台方案设计阶段应用的可行性，进行多方案的对比。对比模型主要信息见表1。主要分析浮筒形状对平台运动响应的影响。

面元模型和Morison模型计算的运动响应RAO对比见图6。由图6可见，横摇响应和垂荡响应RAO面元模型和Morison模型计算结果吻合良好；纵摇响应RAO面元模型和Morison模型计算结果有一定差距。

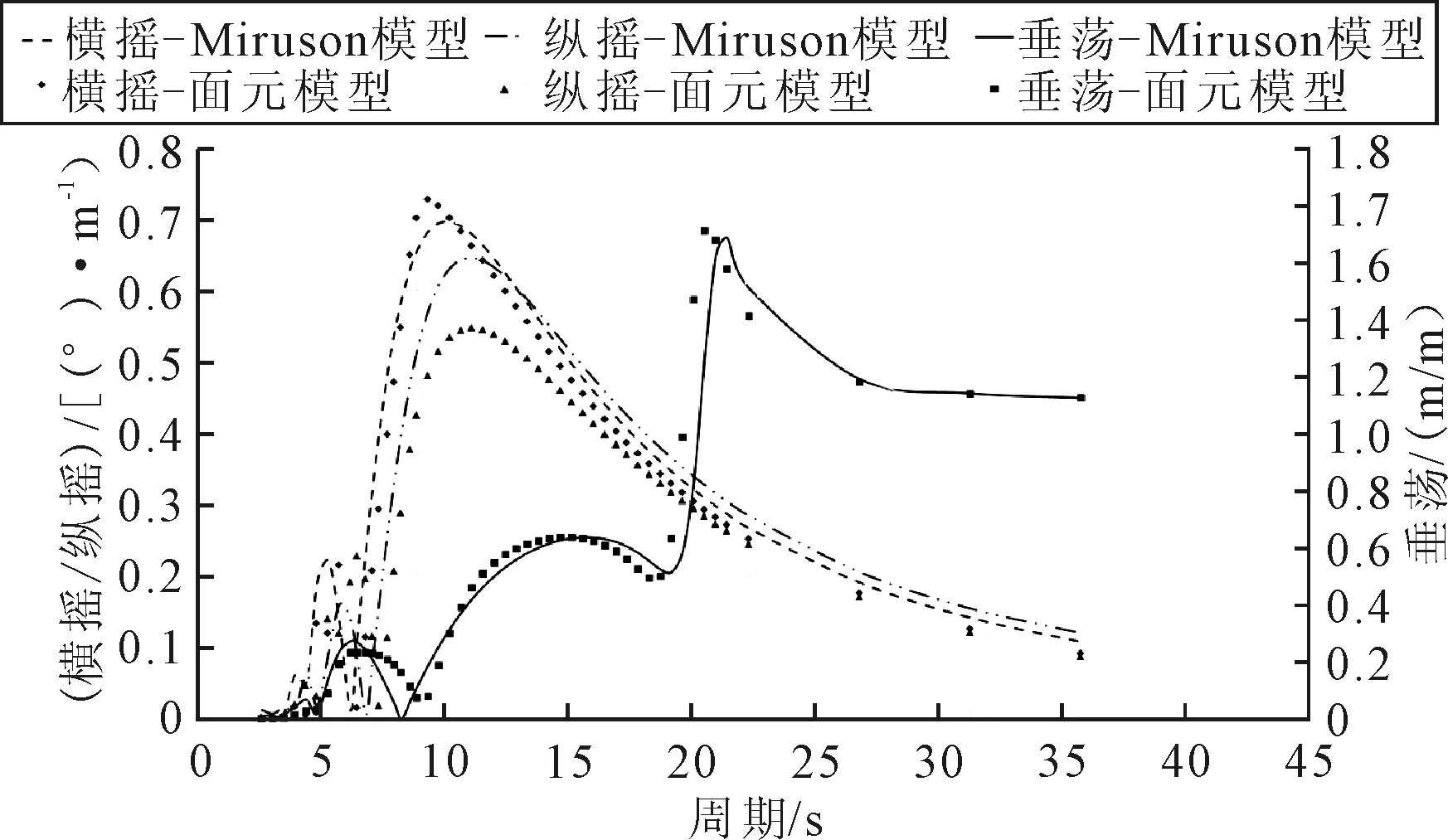
图6 面元模型与Morison模型运动RAO对比

由图7可见，垂荡响应随着浮筒形状的变化，2种分析模型其运动响应RAO曲线的变化趋势及幅值是一致的。

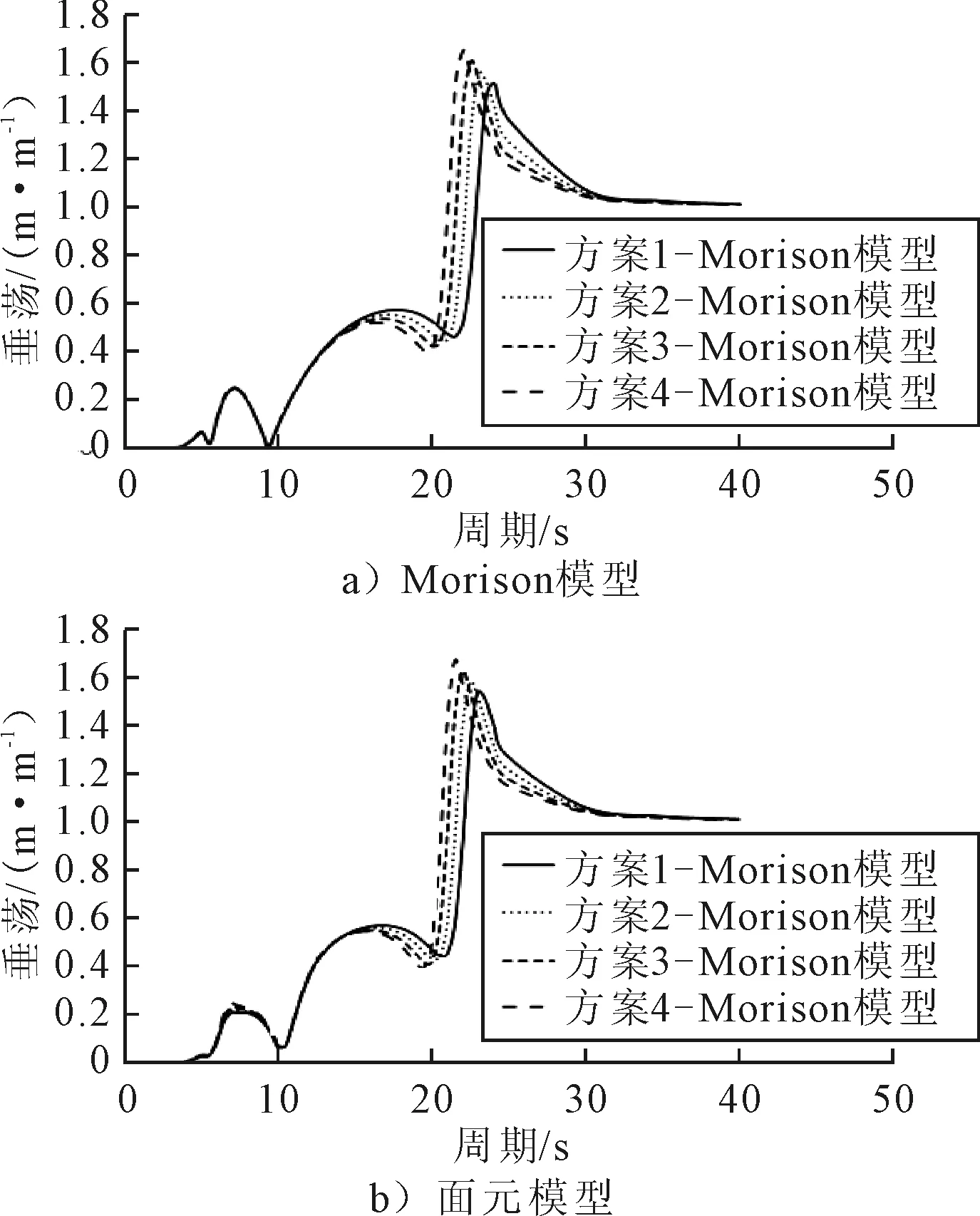
图7 垂荡响应RAO趋势对比

由图8可见，对于纵摇响应RAO，虽然2种模型计算获得幅值大小有一定差异，但是2种分析模型的计算结果的变化趋势是一致的。

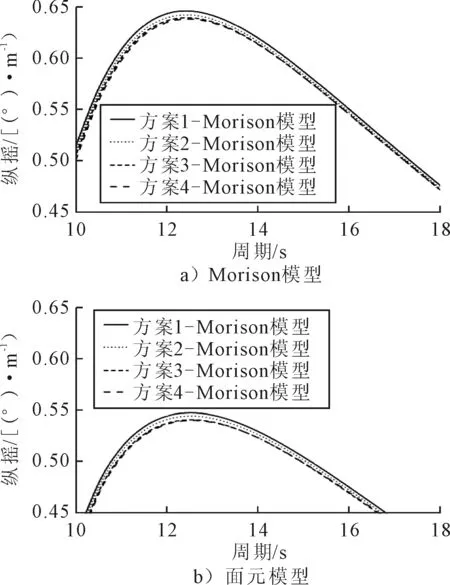
图8 纵摇响应RAO趋势对比

2.3 计算结果分析

自编程序在计算精度上与商业软件一致，可以作为后续研究使用，其优势在于可以自动获取非圆形截面构成的半潜式平台的刚度矩阵等信息，不需要手动进行相关修改，方便批量计算。

Morison模型由于对附加质量系数、阻力系数等进行了简化，2种方法精度上有差异，尤其是纵摇响应。但是从不同浮筒尺寸的变化对运动响应趋势分析来看，2种分析模型的整体变化趋势一致。

由于Morison模型将半潜式平台各组成部分，如浮筒、立柱、横撑等单独简化成细长杆件处理，不考虑各杆件间相互的水动力系数干扰问题，忽略了各水动力系数沿杆件长度方向分布不均匀性影响；同时，忽略惯性力系数等随波浪频率的影响。因而，在计算精度上相比面元模型有一定的差距。但是，Morison模型在计算效率上有明显优势，单个工况整个计算过程不足1 min，建模时间也很少，适合程序批量输入。而基于面元分析方法从模型文件准备到计算，在网格规模不大、结构简单的情况下，一般也需要1～2 h。

3 结论

Morison模型分析方法可以用于半潜式平台概念设计前期的多方案设计中，以节省分析时间，进行海量方案比选，使设计更接近最佳状态。在计算过程中，附加质量和阻力系数均按照常值进行考虑，忽略波浪频率对其的影响，在后续研究过程中可以开展波浪频率对附加质量系数、阻力系数的影响研究，探讨其放入Morison模型中的可行性，以期进一步提高Morison模型的预报精度。同时，由于Morison模型本身计算精度的局限性，虽然在方案设计中可以使用该方法进行方案的比选工作，但最终的方案定型还需要借助面元模型等进行进一步的方案确定，以期获得更加准确的平台性能指标，保证设计质量。