基于集中力的船体强度直接计算加载方案

，，

(中国舰船研究设计中心，武汉 430064)

在船体强度的校核计算中，利用梁理论计算获得船体总纵强度是一种较为传统的方法[1]，但随着有限元方法的出现和计算机软硬件技术的发展，出现整船有限元分析技术[2]。目前有限元强度分析方法是舰船设计过程中校核船体结构总纵强度较为行之有效的现代分析方法[3-5]。通常整船强度计算所施加的载荷主要有：①重力载荷，它是分布在其实际作用区的重力，包括由其派生的货物的侧压力；②静水浮力；③波浪流体动压力；④船舶运动产生的惯性力。以上4种载荷组成了精确的平衡力系，将这些载荷施加于结构有限元模型上实现整船强度的校核。

在采用全船有限元计算船体总纵强度过程中，重力一般按照区域通过控制不同的材料密度系数或加载质量点的形式来实现，静水浮力可按工况的吃水作用在船体外部湿表面上，波浪流体动压力及惯性力则需要根据二维或三维线性理论采用等效设计波法进行计算[6-7]，然后根据计算结果数据对模型进行加载[8-9]。然而，在船体设计过程初期，由于设计深度不足，无法得到重力、静水压力等外载荷沿船长分布情况，此时为初步评估总体方案及船体结构的可行性，如果仅依据由母型船换算得到设计船弯矩分布曲线来开展船体结构的强度校核，则应根据弯矩分布进行反演，获得施加于结构有限元模型上的等效外载荷，并将其以合适的方式加载到模型中，从而实现船体结构总纵强度的校核。针对已知弯矩分布的船舶，考虑将弯矩分布结合相应的结构力学模型计算船体梁所受等效外力，通过变截面空心薄壁单跨梁有限元模型验证外力计算的有效性；同时利用全船有限元模型计算约束节点位置和加载方案的选取对计算结果的影响，最终得到较为合理的约束节点选择方法和加载方案，使得有限元模型中的剪力、弯矩分布与实际船体梁中的剪力、弯矩分布基本保持一致，从而验证加载方案的合理性。

1 等效集中力计算

在船体总纵强度计算中，通常将船体理想化为一变断面的空心薄壁梁，简称船体梁。船舶在波浪上航行时，作用在船体梁上的外力相当复杂，实践证明，船体梁主要承受由重力和浮力引起的总纵弯曲作用，而对于舰船设计过程中计算得到的已知弯矩值，可根据经典的力学分析方法计算作用在船体上的外力。

对于长度为l的某船体梁，切分为n个剖面，中垂工况时其各个剖面弯矩分布值分别为Mi(i=1, 2, …,n)，并假定其艏端点和艉端点所受弯矩值为Mb、Ms，以艉端点为原点，两相邻剖面间间距为li(i=1,2, …,n,n+1)，见图1。

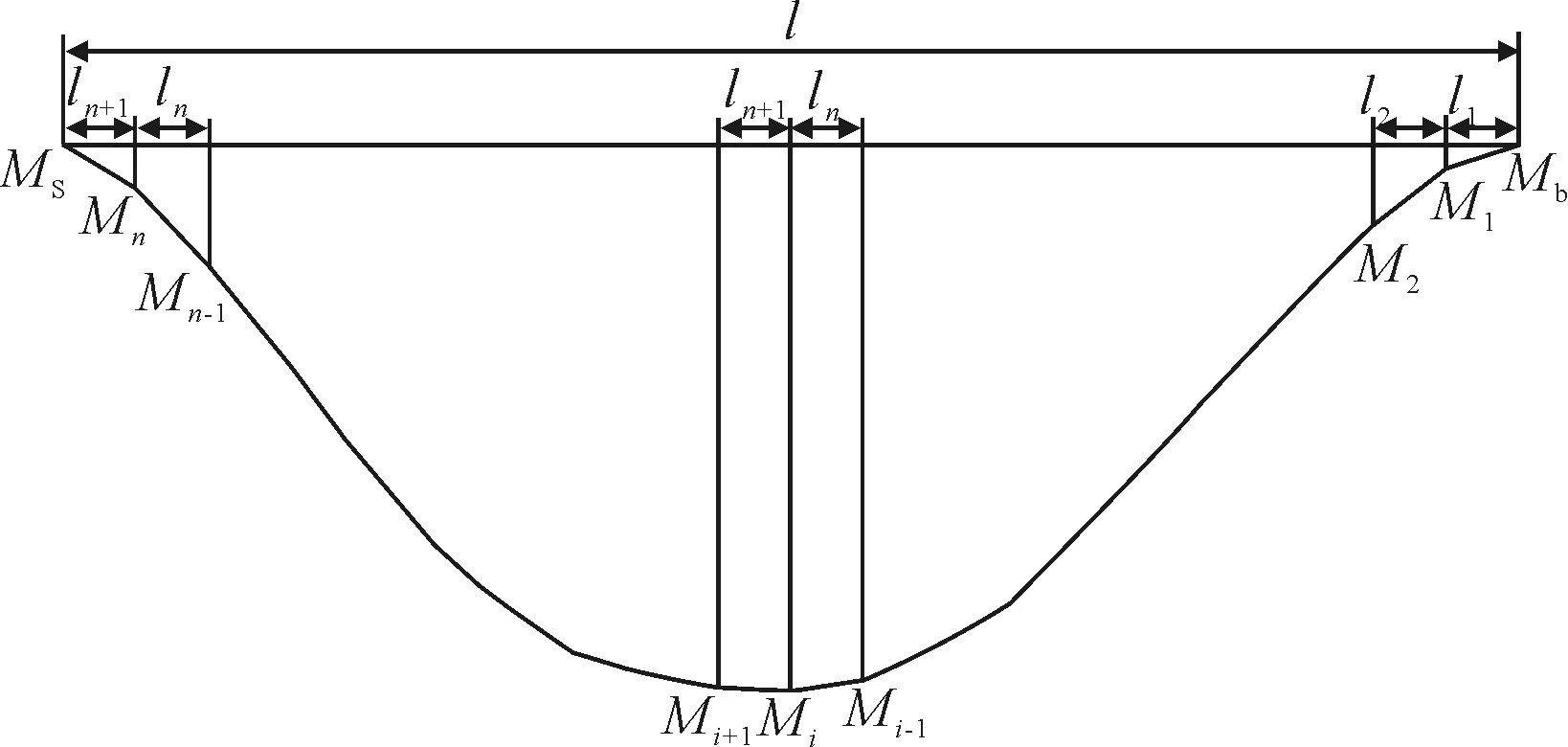
图1 船体梁弯矩示意

图2 船体梁力学模型

假设船体梁各剖面弯矩分别由作用在相应剖面处的集中力Ni(i=1, 2, …,n)及艏艉弯矩Mb、Ms引起，见图2，其等效于每个剖面上的集中力Ni单独作用引起的船体梁弯矩和端面弯矩Mb、Ms作用后引起的船体梁弯矩的叠加[10]，见图3。

图3 计算模型

记各剖面距原点距离为xi(i=1, 2, …,n)，对于图3所示计算模型，每个剖面上的集中力Ni分别单独作用所引起的各剖面所产生的弯矩值MNii为

(1)

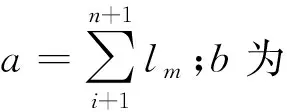
艏、艉端弯矩Mb、Ms作用下各剖面所产生的弯矩值Mei为

(2)

结合式(1)、(2)，将各剖面上集中力Ni分别单独作用引起的船体梁弯矩和端面弯矩作用后引起的弯矩叠加，得到的弯矩即为各个剖面的弯矩值Mi。

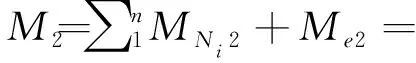
(3)

对方程(3)求解可得作用在船体梁上的集中力为

(4)

由式(4)可知，可由已知的弯矩分布值Mi计算出船体梁的等效集中力Ni，Ni加载到模型中便可对船体梁总纵强度进行直接计算。

2 单跨梁验证计算与分析

2.1 计算模型

假定变截面空心薄壁梁长20 000 mm，将梁分为20站，每站间距1 000 mm，中垂工况时假设船体总纵弯矩M(x)沿船长按正弦曲线分布为[12]

(5)

式中：L为梁的长度；MBY为梁中横剖面总纵弯矩，MBY=-100 MN·m。

计算得到20站弯矩分布及每站等效外力值见表1。

采用ANSYS建立空心薄壁梁有限元模型，梁单元选择Beam188，端部约束见表2，计算模型见图4。

2.2 结果与分析

根据已知弯矩值计算梁外力并加载计算后的剪力、弯矩见图5、6。

由图5、6可知最大剪力为15 643 N，最大弯矩为-99 400 kN·m。由船体梁理论，作用在船体横剖面上的弯矩值M(x)由剪力值N(x)积分而来[1]，反之，若已知弯矩值，则剪力值可由弯矩值求导而来。根据前述已知弯矩分布函数，对式(5)求导，则有

表1 20站弯矩及计算外力

表2 边界条件

图4 空心薄壁梁有限元模型

图5 空心薄壁梁计算剪力

图6 空心薄壁梁计算弯矩

(6)

即已知弯矩及其分布函数时，可对分布函数求导从而求出船体梁剪力分布。由于前述弯矩分布为假定值，则由其求导的剪力分布亦为假定值，其与实际船体梁弯矩及剪力分布均存在出入。为计算简便，仍引用上述弯矩及剪力分布函数。

提取梁模型内部各剖面上节点沿Z方向的剪力，并将其与式(6)计算的剪力对比，见图7。

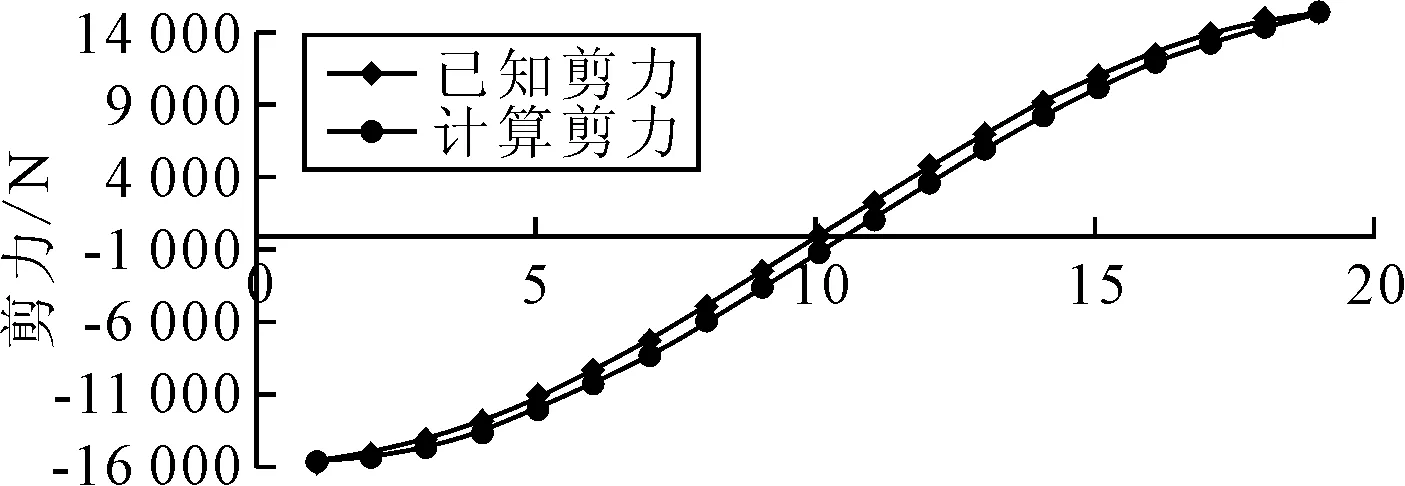
图7 梁模型剪力值对比

由于模型艏艉端节点为约束支点，为除去端部节点支反力影响，仅提取1～19站节点力数据进行比对，同时提取模型中各剖面节点的垂向弯矩，并将其与已知弯矩值对比，见图8。

图8 空心薄壁梁模型弯矩值对比

由对比结果可知，将根据已知弯矩计算得到的等效外力以集中力形式加载到模型中计算后，从模型中提取的节点力系构成的计算剪力分布与已知剪力分布基本一致，但由于网格间距较大，剪力值存在一定误差，从模型中提取的计算弯矩值与已知弯矩较好吻合，由此认为此加载方式合理，计算结果可反映船体梁总纵强度情况。

3 实船计算与分析

3.1 有限元模型

某船总长98.2 m，船宽12.4 m，型深6.0 m，设计吃水3.7 m，肋距0.6 m，纵骨间距0.35 m。采用右手直角坐标系，以肋距为纵向网格间距，纵骨间距为横向网格间距，采用ANSYS建立整船模型，坐标原点为0号肋位，见图9。

图9 整船有限元模型

中垂工况船中横剖面所受垂向总纵弯矩值为-216 624 700 N·m，假设船体总纵弯矩沿船长按式(5)呈正弦分布，则20站弯矩分布见图10。

图10 中垂弯矩值

选取加载剖面时，根据前述等效外力计算公式，由于在已知20站剖面弯矩前提下，其他剖面弯矩一般采用线性插值法计算，因此同一站内加载剖面过多时会出现多处剖面等效外力计算值为零，为避免出现加载剖面外力值为零，同时减小集中力加载对板格计算结果影响，选取水线以下强肋骨及横舱壁所在横剖面与外板交点处节点加载集中力，船体所受外力计算结果见表3。

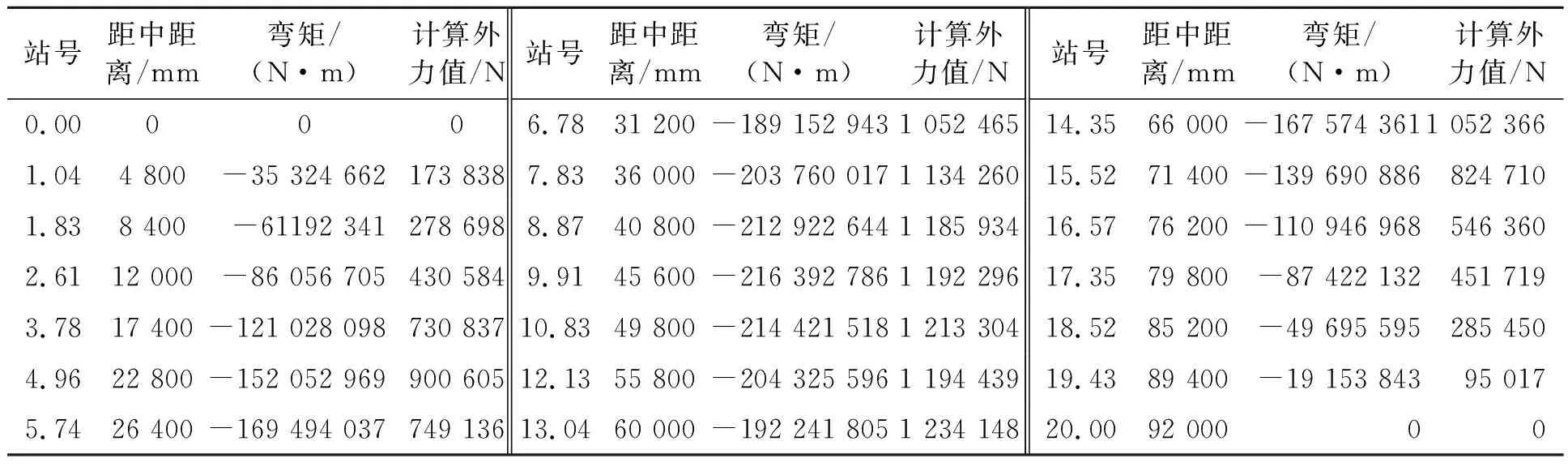
表3 强框架外力计算

3.2 边界条件

采用全船有限元计算船体总纵强度时，有限元模型边界条件设置见表4[13]。

表4 全船有限元边界约束条件

本计算模型艉封板为0号肋位，因此在平板龙骨与艉封板交点处选择节点约束δY；在艉封板水平桁材与外板交点处选择节点约束δZ。由于船底平板龙骨靠船艏处节点仅说明大概位置。对表4中节点1位置分别选取4个不同位置节点约束δX、δY、δZ，分别记为位置1～位置4，见表5。

表5 节点1的位置选择

3.3 计算结果分析

根据表4计算外力值，在船体水线以下强肋骨和横舱壁与外板交点处节点分别加载相应大小集中力，根据表4中节点1位置，分别计算相同边界条件不同节点1位置下船体的总纵强度。不考虑约束支点处应力集中现象，船体各部位构件计算结果见表6。

表6节点1不同位置总纵强度计算结果MPa

构件最大应力位置1位置2位置3位置4外板240.6260.5261.6263.7艏楼甲板179.5192.1192.8194.1主甲板108.8116.3116.7124.0平台甲板161.9169.2169.6170.3内底板223.2236.3240.0238.4龙骨209.7230.2231.3233.5横舱壁187.3196.1196.6197.5

由表6可知，节点1选在20号站及其附近时船体结构各部分构件最大应力差别不大，而选在平板龙骨靠船艏处时应力值偏小。

对于整船有限元模型中所受弯矩值的核算，需首先提取模型中每个横剖面的剪力值，即提取船体模型中每个肋位横剖面上所有节点沿Z方向的节点力的合力，再对提取值进行积分。根据上述4种计算工况，参照2.2中方法，分别提取加载计算后模型中节点力系构成的剪力，同时按式(6)计算模型剪力，将上述提取的剪力分布与理论计算出的剪力分布进行对比，见图11。

图11 剪力值对比

对图11所示剪力进行积分计算，并将计算弯矩与已知20站弯矩值进行对比，结果见图12。

图12 弯矩值对比

由图11可知，4种计算工况模型中节点力系构成的剪力分布与由式(6)求解出的剪力分布均存在差别，节点1选择在位置1时误差最大。且越靠近船中误差越大。

另由图12可知，当节点1选择在20站位置时，模型提取的计算弯矩与已知弯矩基本一致，弯矩最大误差仅为0.71%，选择在20站附近时，模型计算弯矩与已知弯矩有略微差别，其中节点1选择在靠近20号站往艉部整肋位时最大误差为7.66%，选择在靠近20号站往艏部整肋位时最大误差为4.7%，当选择在平板龙骨靠船艏处时，误差较大，最大值为82.42%。由于从0站往船艏逐肋位对剪力进行积分过程中产生累积误差的原因，最大误差点均出现在靠船艏19站位置处，且越靠近艏部误差越大。

当采用集中力法对整船总纵强度进行直接计算时，节点1选择在20站位置时模型中节点力系所构成的剪力和弯矩与给定的设计合成弯矩值基本一致；当20站位置为非整肋位时，应尽量选择在与20站最接近位置整肋位强框架处。

4 结论

1)在弯矩已知前提下，可根据弯矩分布计算船体梁等效集中力，将计算得到的集中力加载到模型中，对船体总纵强度进行直接计算。

2)在给定20站弯矩时，约束点宜选择在0站和20站位置；如果0站和20站位置为非整肋位，则宜选择在临近0站和20站整肋位框架位置。

3)采用集中力法加载方式计算船体总纵强度时，加载节点宜选择水线以下强肋骨及横舱壁所在横剖面与外板交点处节点，同时应尽量避免同一站内加载剖面过密。