基于RSGWPT-LCD的轴承信号故障特征提取及模式识别
王保华, 佟庆彬, 胡 海, 曹君慈, 韩宝珠,卢艳霞, 张卫东, 朱 颖
(1.北京交通大学电气工程学院 北京, 100044) (2.中国兵器工业导航与控制研究所 北京, 100089) (3.华北电力大学新能源电力系统国家重点试验室 北京, 102206)
引 言
滚动轴承是现代机械设备的关键部件,在复杂和恶劣的条件下长期运行会导致滚动轴承产生各种故障。这些故障会使机械运行状态恶化,严重情况下会导致巨大的经济损失和严重的人员伤亡[1]。滚动轴承具有局部故障时,振动信号由于一系列的脉冲冲击,含有丰富的故障信息[2-3]。因此,基于振动信号的分析被广泛应用于滚动轴承的状态监测与故障诊断[4-5]。通过运用信号处理技术,提取故障特征并进行分类识别,可以实现滚动轴承的故障诊断。然而,因为测量的振动信号为非线性和非平稳信号,受复杂的背景噪声影响,有用的故障信息太弱而难以区别。此外,由于滚动轴承的复杂性和结构的相关性,故障通常并不显现为单一故障,使特征提取更加复杂和分类准确度较低。因此,如何有效提取故障特征和准确的故障分类识别已成为保证滚动轴承安全运行的一项紧迫任务。
特征提取的目的是提取机械设备运行状态下的特征用于故障分类。迄今为止,许多信号处理技术已被广泛应用于机械故障诊断领域,例如短时傅里叶变换、维纳分布和小波变换等[6]。小波包变换是小波变换的一种改进方法,它可以分割高频信号并具有更好的时频局部化[7]。第2代小波变换(second generation wavelet transform,简称 SGWT)是一种采用提升方案的新的小波构造方法,与经典的离散小波变换相比,提供了一个完全的空间域变换[8]。但SGWT在分解时由于提升方案固有的分割运算,具有平移变化和频率混叠现象。冗余二代小波包变换具有平移不变性,并且通过去除了分割步骤,预测和更新算子的补零,克服了提升方案的缺点[9]。基于局部特征时间尺度的经验模式分解(empirical mode decomposition, 简称EMD)提供了在时频域对非线性、非平稳信号处理的新方法,可以自适应地将信号分解为一组固有模态函数(intrinsic mode functions,简称 IMFs)。因此,EMD方法对状态识别和滚动轴承故障诊断中的应用受到了更多的关注[10-11]。然而,当EMD方法应用于非线性、非平稳信号时,因为模态混叠、末端效应和无法解释的负频率等问题,原始信号不能被精确分解。局部特征尺度分解方法可以减少无效分量和模态混叠,在处理非线性、非平稳信号方面优于EMD[12-13]。
故障特征提取后,需要对故障特征分类识别。当故障样本有限时,由于人工神经网络自身内在缺陷,使得到的分类结果并不令人满意。基于统计学习理论的支持向量机比人工神经网络泛化能力强,具有良好的全局最优解。然而,支持向量机的实现是基于近似的方法,在实际应用中分类结果与理论分析存在偏差[14]。基于单隐层前馈神经网络的极限学习机(extreme learning machine,简称ELM)和传统方法相比,具有很高的学习速度和良好的泛化性能,可提高分类识别的精度和稳定性[15]。
笔者提出了基于RSGWPT-LCD和ELM相结合的特征提取和分类识别方法。首先,利用希尔伯特变换对原始振动信号进行处理,得到包络信号,基于能量比筛选方法对包络信号实行RSGWPT分解,去除随机噪声,并被分解成一系列含有故障特征的窄频带特征包;然后,利用LCD对特征包进行分解,信号被分解为一系列ISCs, 能量比筛选方法被用来消除ISCs中的虚假低频分量,对提取的各ISCs分量构建初始特征矩阵并进行奇异值分解,将得到的奇异值作为表征各损伤信号的特征向量;最后,将特征向量输入ELM实现故障分类。
1 RSGWPT-LCD故障特征提取方法
1.1 冗余二代小波包变换
第2代小波包变换可以利用提升小波包分解对信号进行预处理,通过在低频段和高频段的每一个尺度进行分解,得到一系列的窄频带分量,实现低频段和高频段的多分辨分析。SGWPT包括剖分、预测和更新3个步骤。剖分是一个下采样过程,会引起频率混叠。信号中的高频成分进行下采样运算后不再满足采样定理,会出现虚假的频率成分。冗余提升方案去除了剖分步骤,不进行下采样运算,故不会产生频率混叠。假设Pj和Uj分别为冗余提升方案中第j层预测算子和更新算子,Pj和Uj的系数可以通过在初始预测算子P和初始更新算子U用0填充Pi和Ur得到
(1)
(2)
根据冗余提升方案和SGWPT,应用Pj和Uj,得到第j层RSGWPT的分解过程
(3)
根据RSGWPT的分解过程可得到重建过程,包括恢复更新、恢复预测和合并3个步骤
(4)
1.2 局部特征尺度分解
局部特征尺度分解方法是一种自适应时频分析方法,基于极值点的局部特征尺度参数, 定义了一种瞬时频率具有物理意义的单分量信号。根据这种方法,通过定义一个基线和迭代-停止准则,任何复杂的信号都可以分解为一系列相互独立的内禀尺度分量和残余项的组合,即
(5)
其中:ISCit为第i个ISC;rnt为残余项。
LCD方法[12]描述如下。
1) 假设 (tk,xk)(k=1,,M) 为信号x(t)的所有极值,根据式(6),(7)分别计算Ak(k=2,,M-1)和相应的Lk(k=2,,M-1)。
(6)
Lk=aAk+(1-a)xk(k=2,,M-1)
(7)
其中:a=0.5。
因为k的值是从2到M-1,需要计算L1和LM的值。通过延拓,得到左右两端的极值点(t0,x0) 和 (tM+1,xM+1),进而可以得到L1和LM。
2) 利用三次样条插值拟合所有的Lk(k=1,,M),得到被定义为上包络和下包络均值的基线SL1(t)。原始信号和基线SL1(t)的差值为第1个分量h1(t)
h1(t)=x(t)-SL1(t)
(8)
如果h1(t)满足ISC 的定义,即为一个ISC分量,输出h1(t)并令ISC1=h1(t)。
3) 否则,将h1(t) 作为原始数据,重复上述步骤,经过m次迭代运算,直到h1m(t)满足ISC分量条件,则h1m(t)为第1个ISC分量,记为ISC1(t)。
4) 将第1个ISC分量从原始信号x(t)中分离出来,得到一个新的信号r1(t),即
r1(t)=x(t)-ISC1(t)
(9)
5) 将r1(t)作为原始信号,重复上述步骤,得到第2个内禀尺度分量。重复n次,直到rn(t)单调或为一次函数为止。因此,x(t)被分解为n个内禀尺度分量和一个单调或常函数的残余项之和,如式(6)所示。终止判据采用标准偏差法,将第1个内禀尺度分量从原始信号x(t)中分离。
1.3 基于两步筛选的RSGWPT-LCD故障特征提取
利用LCD进行信号分解时,由于实际测量信号包含比较丰富的频率成分,分解得到的ISCs可能包含很宽的频带,因此很难获得一个窄频带内的单分量信号。RSGWPT方法具有正交性、完备性以及局部性等优点,在信号分解时,具有更好的局部时频定位能力和更窄频带内的信号分解能力。为了准确提取故障特征,这里给出基于能量比两步筛选方案的RSGWPT-LCD信号分解方法。带有能量比筛选的RSGWPT作为预处理器将频率分量分割为一组窄频带信号,带有能量比筛选的LCD在窄频带内提取故障特征。同时,能量比两步筛选方案可以有效消除RSGWPT分解的冗余系数和LCD分解的冗余分量。
原始信号x(t)可以写为
x(t)=X0,1(k)k=1,2,,K
(10)
其中:K为信号长度。
对信号x(t)实施Hilbert变换,得到包络信号xe(t)。对包络信号xe(t)进行j层RSGWPT分解,得到2j个长度为K/2j的子频带系数Cj,m,即
(11)
其中:j为分解对应的层数;m为在特定层数节点的次序;每个小波包树的结点由一组整数(j,m)编号。
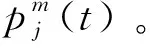
(12)
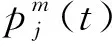
(13)
对于小于阈值0.99的能量比,相应的Ci,n(t)被看作为真正有意义的ISC分量,并存储在数据集Cs(t)中。否则,将被视为冗余的ISC分量而被消除掉。最终应用Hilbert 变换可以得到Hilbert谱和边际谱。
1.4 仿真信号分析
为了验证RSGWPT-LCD方法的有效性,给出式(14)所示的调制信号。为了模拟实际情况,在模拟信号中加入信噪比为-1dB白噪声,以采样频率fs=1 024Hz对信号进行离散化采样,采样点数为1 024。信号由两个载波频率分量(150和400Hz)组成,且分别在时间区间 [ 0,0.5 ]和[ 0.5,1 ]被20和60Hz调制。
x(t)=
(14)
图1为仿真信号的时域波形图。图2为对仿真信号进行Hilbert包络得到的包络谱图。由于噪声掩盖了信号特征,无法从时域图和原始包络谱图中得到特征频率。
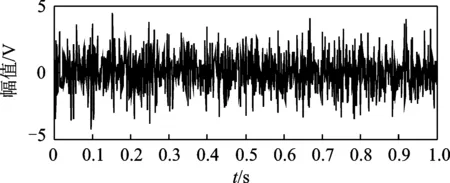
图1 仿真信号时域图Fig.1 Time domain plot of the simulated signal
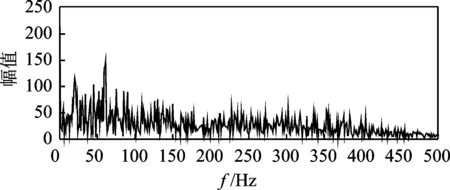
图2 仿真信号包络谱图Fig.2 The envelop spectrum of the simulated signal
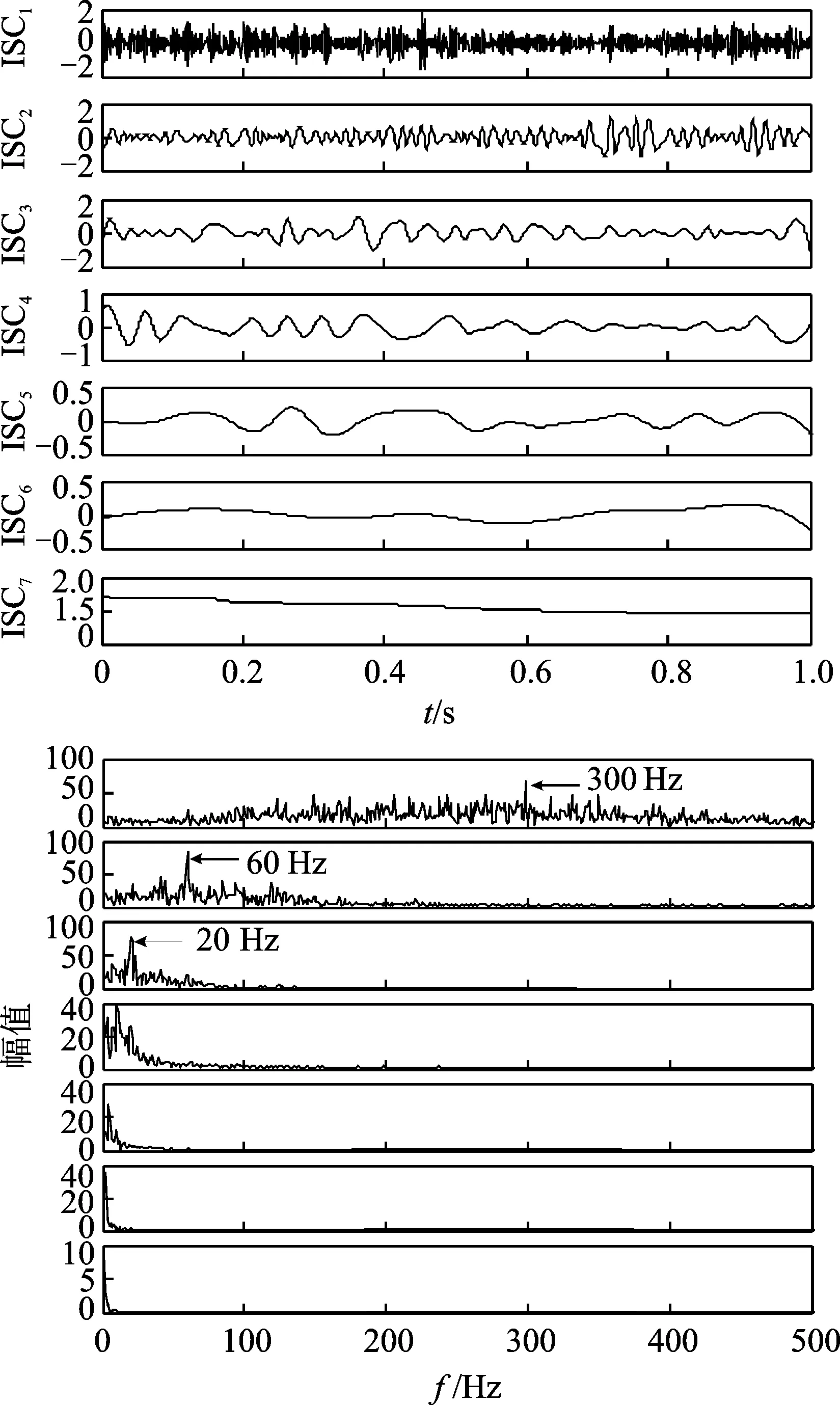
图3 LCD分解结果和相应的ISCs频谱图Fig.3 The decomposition results with LCD and corresponding frequency spectrums of ISCs
分别利用LCD和提出的RSGWPT-LCD方法对仿真信号进行分解,分解结果和相应的频谱图如图3,4所示。图3中,ISC1包含调制频率的倍频,ISC2和ISC3分别包含调制频率60 Hz 和20Hz,其余的ISC包含很多冗余的频率分量。从图4可以看到,所提出的方法能够清楚地检测到频率为20 Hz和60 Hz的调制频率,且分解结果中并没有无意义的冗余分量。图5为应用RSGWPT-LCD方法得到的Hilbert谱和边际谱。可以看出特征频率明显突出并去除了无意义的冗余频率分量,可以有效消除信号噪声并提取信号的频率特征。
2 极限学习机
极限学习机是一种基于单隐层前馈神经网络的机器学习算法。传统的神经网络学习算法需要人为设置大量的网络训练参数,很容易产生局部最优解[15]。ELM只需要设置网络的隐层节点个数,在算法执行过程中不需要调整网络的输入权值以及隐元的偏置,且产生唯一的最优解,因此该算法具有学习速度快且泛化性能好的优点。
设存在任意N个不同样本(xi,yi)∈Rn×n,其中:xi为输入向量;yi为相应的期望输出。典型的具有L个隐节点的单隐层前馈神经网络可表示为
(i=1,2,,N)
(15)

式(15)可以简化为
Hβ=Y
(16)
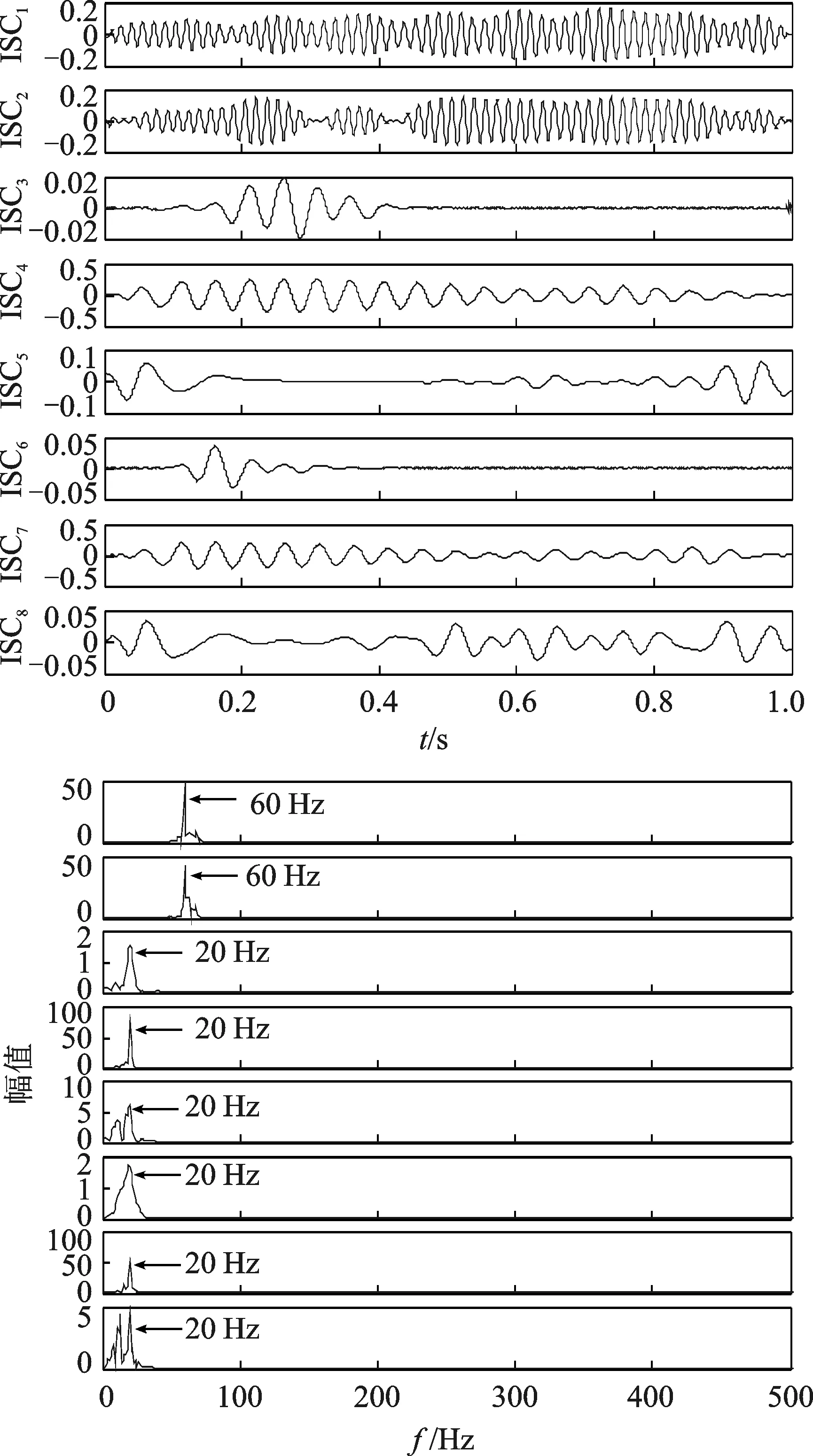
图4 RSGWPT-LCD分解结果和相应的ISCs频谱图Fig.4 The decomposition results with proposed RSGWPT-LCD and corresponding frequency spectrums
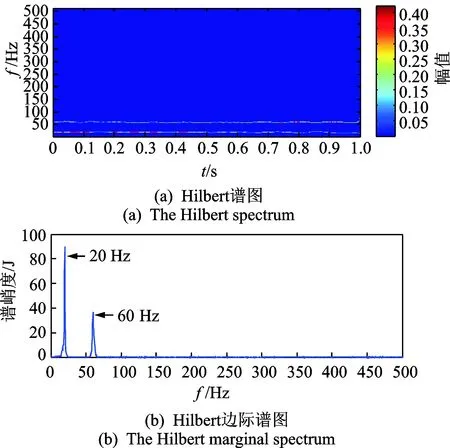
图5 仿真信号利用RSGWPT-LCD方法Fig.5 The signal simulated using proposed method
其中
为了确定网络结构以拟合N个不同样本输入输出来取得任意小的非零误差,可以随机选择L(L≤N) 个隐节点。该隐节点具有随机的参数wj和偏置量bj,从而确定H。通过计算式(16) 的最小二乘解,输出权值为
β=H+Y
(17)
其中:H+为隐层输出矩阵H的Moore-Penrose推广逆运算。
3 试验与分析
为了进一步验证所提出方法的有效性和可行性,给出实际滚动轴承的振动试验。振动数据取自美国凯斯西储大学轴承数据中心提供的数据[17],轴承型号为6205-2RS JEM SKF,试验中转速设置为1 797 r/min,采样频率为12 kHz,采样点数为1 024,故障位置覆盖外圈、内圈和滚动体,经计算滚动轴承滚动体、外圈和内圈的的故障特征频率分别为141.17,162.19和107.37Hz。
图6为滚动轴承滚动体的时域故障振动信号。可以看到,滚动体故障振动信号中存在明显的冲击信号,但成分复杂,故障特征信息淹没在强背景噪声中,不能从中识别出故障特征频率,因此,需要对其进行分析并与相应的特征频率(141.17 Hz)进行比较。对故障信号进行包络分析,如图7所示。可以看到,在频谱图中虽然存在故障特征频率,但被噪声和谐波干扰,因此单纯的包络谱分析无法给出准确判断故障状态的信息。
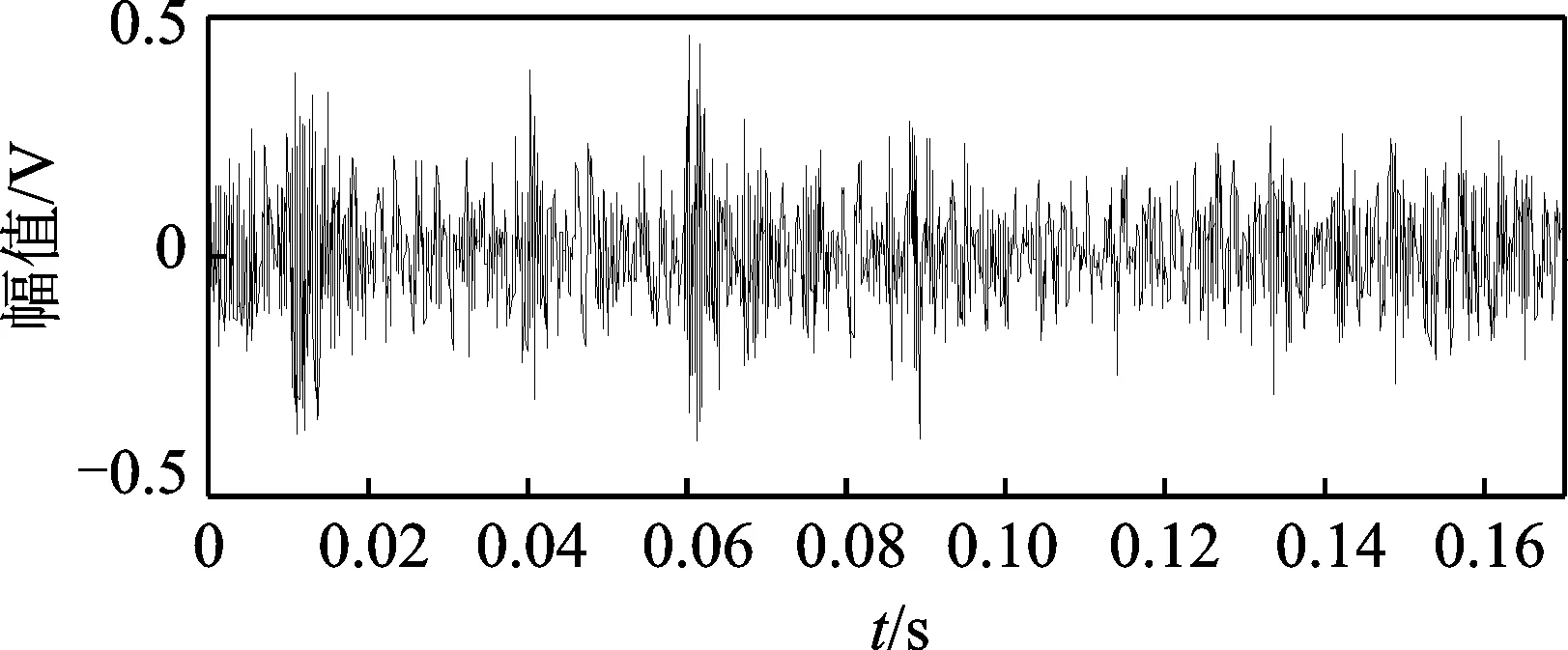
图6 滚动体缺陷信号时域图Fig.6 Time domain plot of the rolling element defect signal
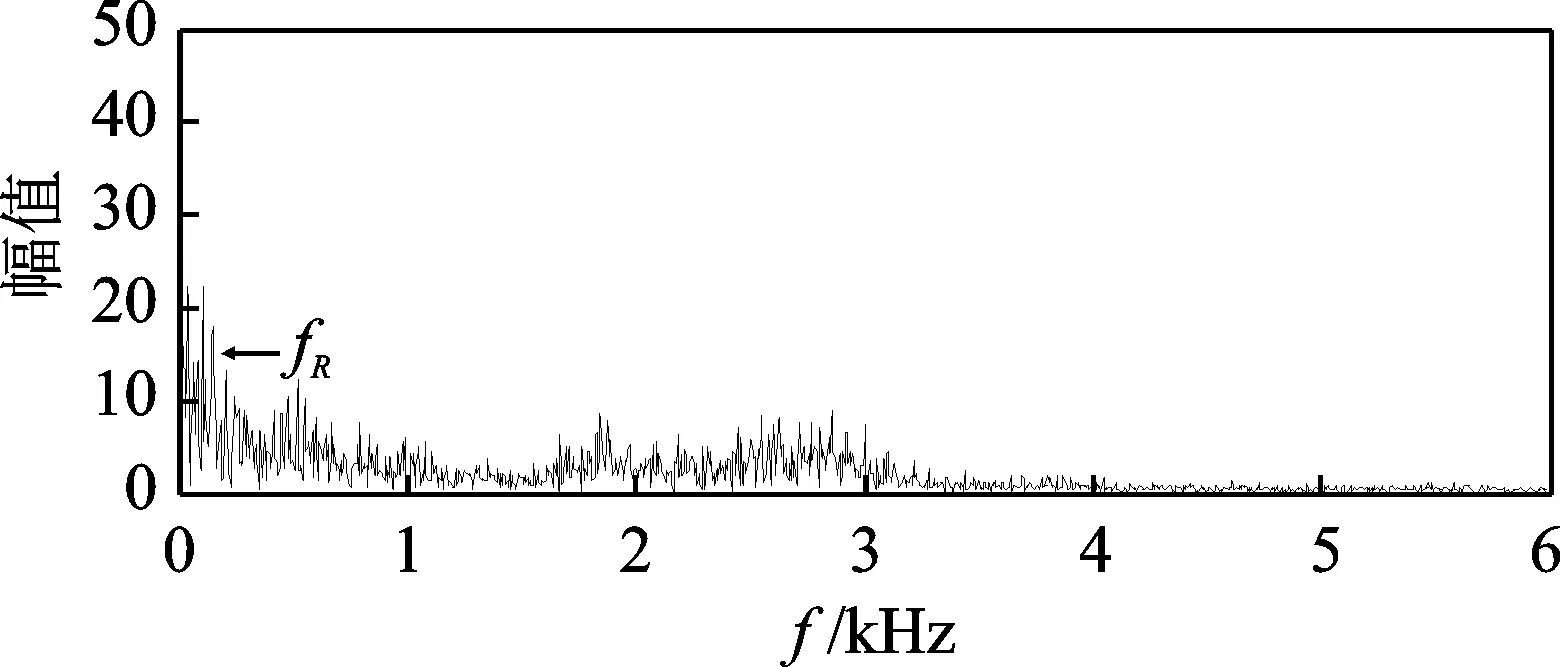
图7 滚动体缺陷信号包络谱图Fig.7 The envelope spectrum of the rolling element defect signal

图8 应用RSGWPT-EMD的Hilbert边际谱图Fig.8 The Hilbert marginal spectrum of the rolling element defect using RSGWPT-EMD

图9 应用WPT-LCD的Hilbert边际谱图Fig.9 The Hilbert marginal spectrum of the rolling element defect using WPT-LCD
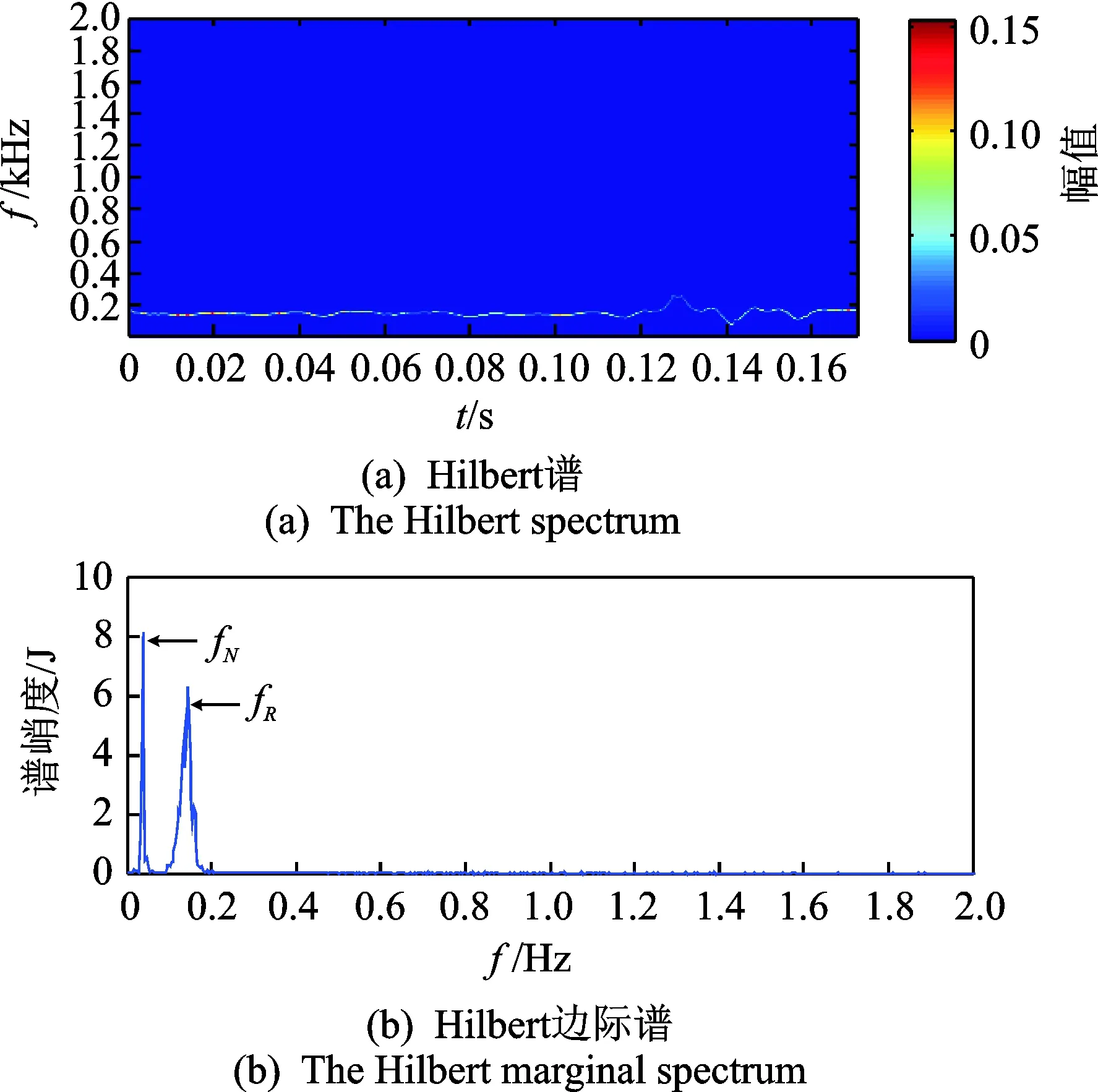
图10 RSGWPT-LCD处理结果Fig.10 The results using RSGWPT-LCD
为了有效提取滚动轴承故障特征,基于两步筛选过程,采用RSGWPT-EMD,不带筛选的小波包换和局部特征尺度分解(wavelet packet transform, local characteristic-scale decomposition,简称WPT-LCD)和笔者提出的方法,对图6所示的滚动体振动信号进行处理,得到图8~10所示的Hilbert 边际谱图。可以看出,相比于采用RSGWPT-EMD和WPT-LCD方法的处理结果,提出的RSGWPT-LCD方法由于有效去除噪声和自适应地ISCs选择,提供了更好的故障特征提取结果。可见,所提出的方法可以将滚动轴承发生故障时产生的故障特征清楚地提取出来。
为了给出直观的分类结果,经过RSGWPT-LCD方法提取滚动体故障特征之后,利用ELM实现故障模式识别。由于SVD本身具有良好的稳定性、尺度不变性和旋转不变性等特性,因此利用SVD对提取的各ISCs分量进行分解,并将得到的奇异值作为表征各损伤信号的特征向量输入到ELM实现故障分类。每一个振动信号代表一个工作状态,将前12k个点分为40个子信号,每一个子信号代表一个样本。因此,每种工作状态可以获得40个样本,7种工作状态共计有7×40个样本。样本被分为训练样本和测试样本,3个数据集的详细描述如表1所示。为了提高分类精度,每次试验重复30次,3个数据集的平均分类精度如表2所示。
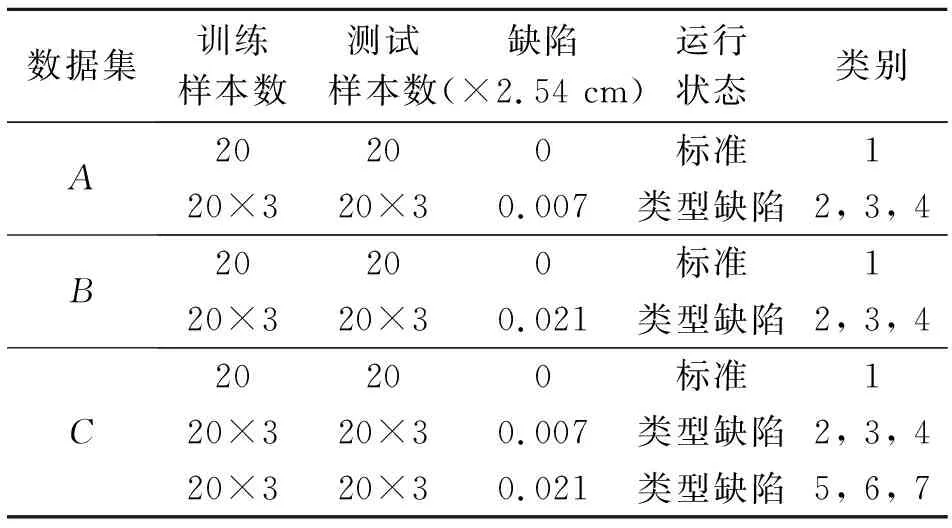
表1 样本数据集详细分类
表2基于不同方法的ELM分类结果%
Tab.2TheclassificationresultsofELMbasedondifferentmethod
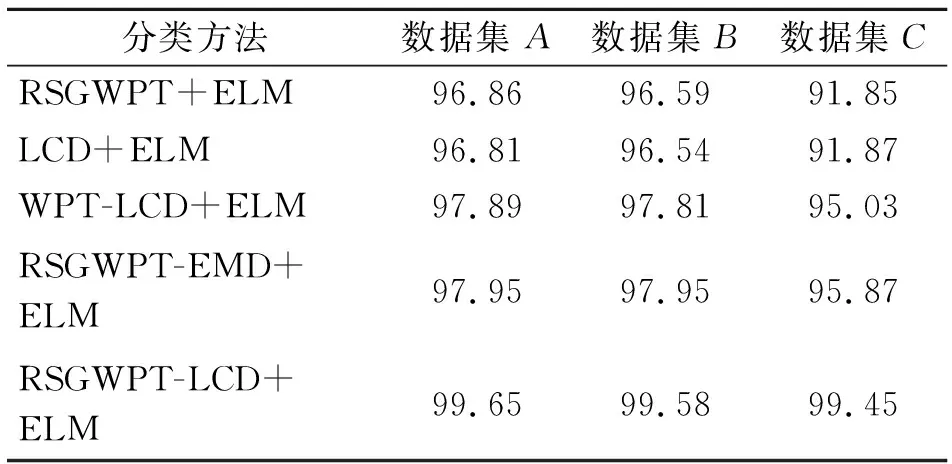
分类方法数据集 A数据集B数据集CRSGWPT+ELM96.8696.5991.85LCD+ELM96.8196.5491.87WPT-LCD+ELM97.8997.8195.03RSGWPT-EMD+ELM97.9597.9595.87RSGWPT-LCD+ELM99.6599.5899.45
为了提高分类精度,每次试验重复30次,利用不同方法对3个数据集进行分类识别,平均分类结果如表2所示。可以看出,运用所提出的方法对数据集A,B和C进行检验,正确识别率分别为99.65%,99.59%和99.45%,表明该方法能够对滚动轴承振动信号进行有效的分类识别。RSGWPT-LCD融合了RSGWPT和LCD方法的优点,其双层筛选机制可以有效去除冗余特征,相比于RSGWPT和LCD的分类结果,所提出的方法给出了更好的分类结果。同时,RSGWPT-LCD+ELM方法的分类结果也优于WPT-LCD+ELM 和 RSGWPT-EMD+ELM方法的分类结果。另外,在数据集C的情况下,所有方法的分类精度均低于数据集A和B的分类精度,这是因为数据集C考虑了7种情况的工作状态,数据量较大,而数据集A和B分别考虑了4种情况的工作状态。相比于其他方法,所提出的方法在数据集C中的分类结果更为突出,分类精度也高。
在滚动轴承的故障特征提取和模式识别中,文献[18]利用相空间重构提取故障特征,并将提取到的故障特征输入半监督极限学习机,在测试样本为40组的情况下得到的分类准确率为98%。文献[19]利用小波分析提取滚动轴承振动信号的故障特征,利用改进的极限学习机并结合遗传算法对故障特征进行分类识别,得到的分类正确率93.5%。文献[20]利用EMD提取与原信号相关度较大的故障特征,并输入到极限学习机,得到的最终分类准确率为92.5%。与上述方法相比,笔者提出的方法是对分类识别前的故障特征提取方法进行改进,从而提升故障识别准确率。以最终测试所得的分类准确率来说,笔者提出的方法准确率可达99%以上,且测试样本为140组,分类精度更高,这说明在故障特征提取方面是有效的,该方法具有适用性。
4 结束语
针对滚动轴承在强噪声环境下故障信号微弱、故障特征难以提取等问题,为了有效提取振动信号故障特征和提高分类识别精度,提出了一种基于RSGWPT-LCD和ELM的滚动轴承故障诊断方法。利用包含不同频率分量信号和实际轴承振动信号对所提出的方法进行验证,并与其他方法进行比较。所提出的方法具有较强的降噪能力、易于实现,能准确有效地提取隐藏在强噪声和强干扰背景下的故障特征信息,分类识别精度较高,适用于轴承故障的监测与诊断,具有较高的工程使用价值。

