新型μ律压扩法降低OWPM系统的PAPR

黄娴 南昌工学院人工智能学院 南昌市 330108

徐宁 国家计算机网络应急技术处理协调中心江西分中心 南昌市 330000

0 引言

随着人们对无线通信网络宽带化的需求不断增强，传统传输技术存在的问题日益突出。由于正交小波包复用(OWPM）系统在频谱利用率、抗干扰能力和子信道配置等问题上具有比传统的正交频分复用系统(OFDM)更高的优势，所以越来越受到科研工作者的关注[1-5]。但是，OWPM系统作为一种新型的多载波调制通信系统，同样存在某个时刻多个子载波同相累加产生的高峰均功率比问题，从而对发送端的功率放大器提出非常高的线性要求。若无法满足，那么一旦信号峰值进入功率放大器的非线性区域，就会产生信号的畸变以及子信道间的互调干扰和带外辐射，导致子载波之间的正交性破坏，最终降低系统的性能。因此，有必要寻求一种本质上解决信号高峰均功率比(PAPR）问题的方法。本文主要针对预畸变方法中的μ律压扩变换法[6-9]进行深入研究，针对传统算法的不足之处加以改进，并进行仿真比较。实验仿真证明，经过改进后的μ律压扩变换法确实能够大大地降低发送端的PAPR值，具有一定的理论意义。

1 基本原理

μ律压缩扩展法（简称μ律压扩法）是一种采用非线性操作来降低信号PAPR值的方法。和阈值限幅法所不同的是，μ律压扩法从语音信号的非均匀量化处理中衍生而来，函数表达式并不像阈值限幅法那么简易；其次，μ律压扩法是以功率分布为基本思想实现信号的数值变换。图1即为μ律压扩法降低PAPR的系统原理框图。

图1 μ律压扩法降低PAPR的系统原理框图

2 新型μ律压扩法

传统μ律压扩法的基本原理是放大小幅值信号的功率，同时缩小大幅值信号的功率。通过适当的调节压缩扩展变换因子μ，可以保证压扩前后信号的平均功率基本保持不变，不会给功率放大器造成负担。发送端函数表达式为：

其中μ为压扩因子，通常取小于等于5； 为信号的平均幅值，也即μ律压扩的转折点； 表示经小波包调制后的信号。

然而，传统μ律压扩算法硬件实现比较复杂，成本高。为降低硬件实现难度，本文提出一种分段函数算法，即

该算法将大于拐点处的信号进行简化压缩处理，而保持小于或等于拐点处的信号幅值不变，这样一来，不仅减少了信号畸变数，有效的压缩了峰值信号，同时能降低硬件实现的复杂度，是一种多方考虑后的有效算法，具有一定的实用价值。具体推导过程如下。

首先，以最原始压扩函数为出发点，其数学表达式为：

其次，一个合适的压扩变换函数应该满足两个要求：

图2 最原始压扩函数曲线图

从图2中可以知道：最原始压扩函数的压扩转折点不随μ的取值变化而变化，而是固定为1，也就是说当时，信号被放大，当时信号被压缩，由此证明该函数满足上面所提的第一个要求。但对于第二个要求，由于最原始压扩函数的压扩转折点固定不变，所以对于不同信号就未能确保信号在压扩变换前后的平均功率基本保持不变，为此希望能对压扩变换的转折点进行动态选择，也即有必要对该最原始压扩函数关于转折点进行归一化处理，得到修正后的μ律函数为：

其中，V为压扩变换的转折点。

最后，为了硬件物理可实现，可以将信号X向左或向右平移一个非常小的量，这里采用X＝X+0.001，得到最终函数：

该函数曲线图如图3所示。可以看出，由于函数关于转折点进行归一化处理后，便可以根据预先设定的值动态选择压扩转折点，最终确保信号变换前后的平均功率基本保持不变。

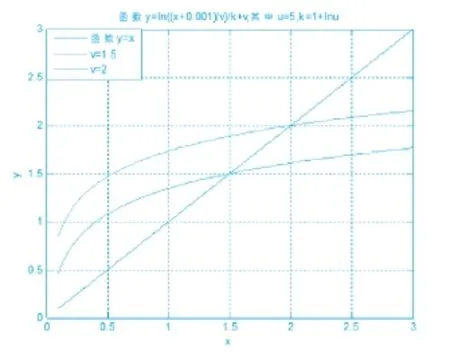
图3 新μ函数曲线图

3 实验仿真结果

实验采用Matlab软件进行仿真分析。仿真环境为：随机产生长度为N=2048的源信号序列，总符号数为10000，采用4QAM进行星座映射，子载波数为8，同时选取db4小波作为小波包基. 由于信号峰均比的CCDF是在发送端进行计算的，不涉及信道部分，所以算法的PAPR抑制性能不受信道的影响。但为了验证算法的正确性，在模拟信道中加入了高斯白噪声进行BER性能仿真比较。

（1）PAPR抑制性能

图4是无压扩和采用传统μ律压扩法和改进μ律压扩法后的信号PAPR分布曲线。可以看出，无论是经过传统μ律压扩算法处理还是改进的μ律压扩算法，在PAPR抑制性能上都较无压扩系统有很大程度的提高。而改进的μ律压扩法具有最好的PAPR抑制性能。

图4 改进μ律压扩与传统μ律压扩PAPR抑制性能比较

（2）误码率性能

实验模拟高斯白噪声信道，对信道进行1000次仿真统计。从图5中可以看出，当信噪比小于15dB时，改进μ律压扩算法的BER性能略差于传统μ律压扩算法，但当信噪比比较高时，却呈现出改进μ律压扩算法更好的BER性能曲线，由此也证明了改进算法的有效性与正确性。

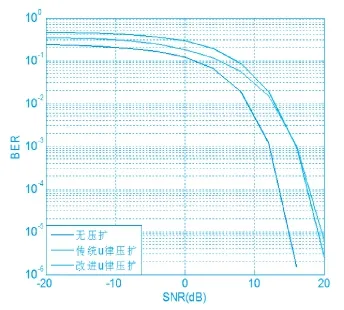
图5 改进μ律压扩与传统μ律压扩BER性能比较

综合分析可知，改进的μ律压扩算法相较传统的μ律压扩算法，不仅降低了系统实现的复杂度，而且能够在尽量不影响BER性能的前提下大大提升系统的PAPR抑制性能，具有不错的应用前景。

4 结语

本文主要对μ律压扩法进行研究，提出一种新型μ律压扩法降低OWPM系统的PAPR值。理论和仿真结果均显示，改进后的μ律压扩法相比改进前的算法有了相对应的性能提升。