岭回归分析在解决经济数据共线性问题中的应用

王 锐

（上海理工大学 管理学院，上海 200093）

引言

多元线性回归模型是处理数据常用的方法，但经济数据集中高维数据频繁地出现，使得经典线性回归统计方法受到较大冲击。较高维数据常会出现多重共线性问题[1]。多重共线性不是模型设定的错误，但使用传统的最小二乘法（OLS，Ordinary Least Squares）处理这类经济数据时，往往会出现回归系数计算不稳定、模型解释性较差、预测准确性较低等问题[2]。目前，岭回归（Ridge Regression）是处理严重共线性常用方法[2]。Hoerl于1962年最早提出岭回归，这是一种改进的最小二乘估计法，到1970年，Hoerl&Kennard对该方法进行了更详细的讨论[3]。

一、多重共线性检验

一般，多元回归模型假设各个预测变量之间没有很强的依赖关系，即模型[4]：

或用矩阵形式表示：

预测变量 X1，X2，…，Xp是相互独立，或（X′X）不接近奇异矩阵，但当预测变量间存在较强的线性关系，称之为（多重）共线性问题。通常，多重共线性问题的产生有如下原因：经济变量相关的共同趋势；滞后变量的引入；样本资料的限制[4]。

方差膨胀因子（VIF，Variance Inflation Factor）[2]是度量共线性常用的方法，VIF是回归系数OLS估计平方误差之和的期望与正交条件下期望的比值，定义式为：

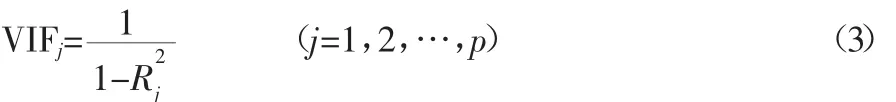
通常带截距项OLS回归，VIFj取值从1到无穷大。当VIFj=1时，认为模型中各变量间没有任何线性关系，当VIFj值逐渐增大，变量之间逐步走向共线性，当VIFj＞10时，认为模型存在多重共线性[2]。

二、岭回归分析

（一）岭回归参数估计

对于回归模型，当预测变量具有较高的共线性时，岭回归提供了一种有效的估计方法，其基本思想[2]是：对回归模型进行中心化和标准化处理，建立模型：

其中，响应变量 Z=（Z1，Z2，Zj，…，Zp），Zj是原始数据，是通过以下变换所得：

那么岭回归正规方程组变为：

由上式中解得参数α估计为：

上式中，岭参数K值选取准则是调和总方差和偏倚两者的关系，过小或过大都会导致估计误差扩大[2]。常用方法包括固定点方法、迭代方法、岭迹法[2]，其中，岭迹法是一种图像方法，通过观察岭迹图选取合适的K值。一般要求各岭回归系数估计值基本稳定，即岭迹平稳。

（二）岭回归进行变量选择

实际应用中，回归模型所涉及的预测变量往往不是事先确定的，确定一组优秀的变量子集不仅能更清晰地解释预测变量和响应变量之间的关系，同时能提高预测精度。

岭回归能产生一个系数稳定的回归方程，借鉴岭迹法进行变量剔除，该剔除过程有两个准则[2]：第一准则，删去那些系数稳定但绝对值很小的预测变量；第二准则，剔除那些不稳定但是回归系数θ^j（K）随着K值的变大而趋向于0的变量。

第一次岭回归剔除一个或几个变量后，可重复以上过程，直到剩下的变量岭迹稳定，最后运用OLS对所选变量进行回归，但若所保留变量仍有共线性，可考虑使用岭回归方法进行参数估计，建立岭回归模型。

三、实例分析

实例分析为我国就业情况与相关经济指标的关系，数据为1997—2016年的宏观经济数据，源于《中国统计年鉴》[5]。指标选择参考Longley数据集[6]，设定1个响应变量和5个预测变量组成的宏观经济数据集，包含就业人员（万人）（Y）、年份（X1）、人均国内生产总值（元）（X2）、年末总人口（万人）（X3）、法人单位数（个）（X4）、城镇登记失业人数（万人）（X5）。

本文为研究以上5个变量对就业人员的影响，拟建立多元线性回归模型，即：

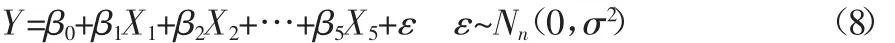
（一）OLS估计及共线性检验

为了确保模型设定合理性及预测结果有效性，需要对模型进行回归诊断。首先，使用SPSS软件运用OLS回归分析，结果（见表 1）。

表1 数据OLS回归分析结果

由表1可得，用OLS拟合线性回归方程为：

虽然从表1中R2来看，模型解释性很好，同时标准化残差检验显示出模型无明显误设问题，但OLS拟合回归方程中p值及部分系数符号并不合理。

所以，考虑把两两预测变量的散点图排成矩阵图1）。通过散点图—相关系数矩阵观察可得，各指标相关系数都在0.75以上，散点图基本都呈线性模式。

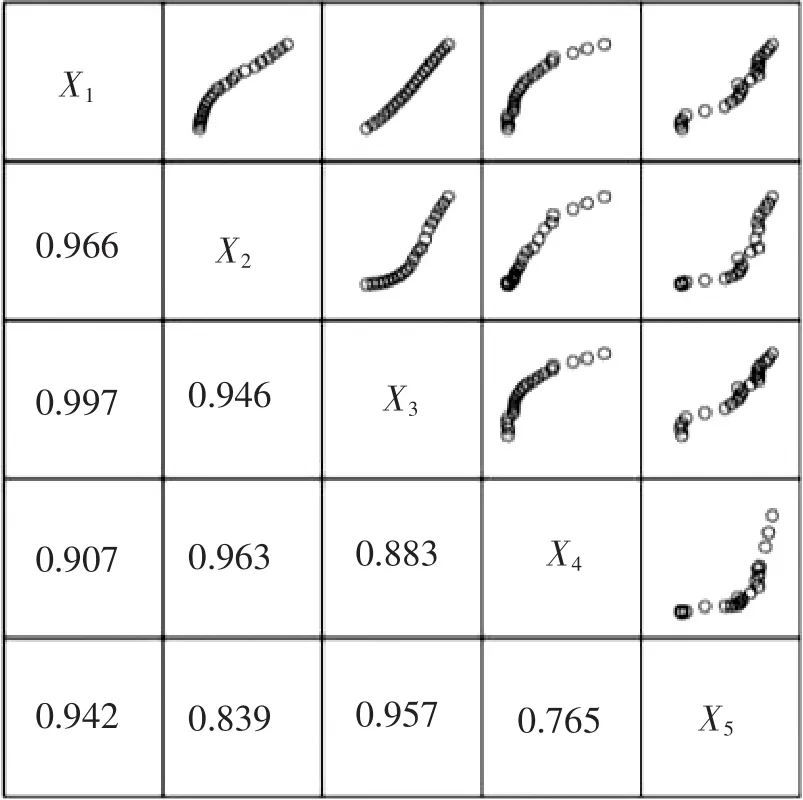
图1 散点图—相关系数矩阵

再使用SPSS软件中共线性检验功能，可以得到各变量方差膨胀因子：

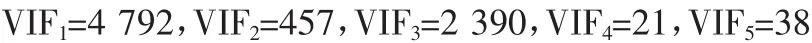
该经济数据的VIF值的变化范围为21—4 792，预测变量VIF值均大于10，由检查数据集中预测变量的相关系数，方差膨胀因子VIF，都说明该数据存在严重的多重共线性，必须采取措施消除共线性的影响。

（二）变量选择

运用SPSS软件实现对经济数据岭回归分析，岭参数K的取值从0～0.2，间隔为0.005，共记录了40个岭参数取值，做岭迹图。对全部5个变量岭迹进行分析，发现岭迹比较杂乱，且变量之间存在高度线性关系，故首先考虑剔除部分变量。

根据选择变量准则，先考虑剔除X4，因为标准化回归系数估计变化较稳定，但绝对值趋于0；当K=0时，变量X3的标准回归系数最大，但当K增加时迅速下降，变量X1则变化相反，且当K增大后，X1、X3与X5岭迹几乎重合，三者相关系数达到0.94以上，三个变量可近似合并为一，故试着保留X3。最终，去掉X1、X4、X5（剔除这 3 个变量不违反经济常识）。再次，进行岭回归分析，生成2变量的岭迹图，图中岭迹基本稳定。最终，选择人均国内生产总值（元）（X2）、年末总人口（万人）（X3）作为模型预测变量。

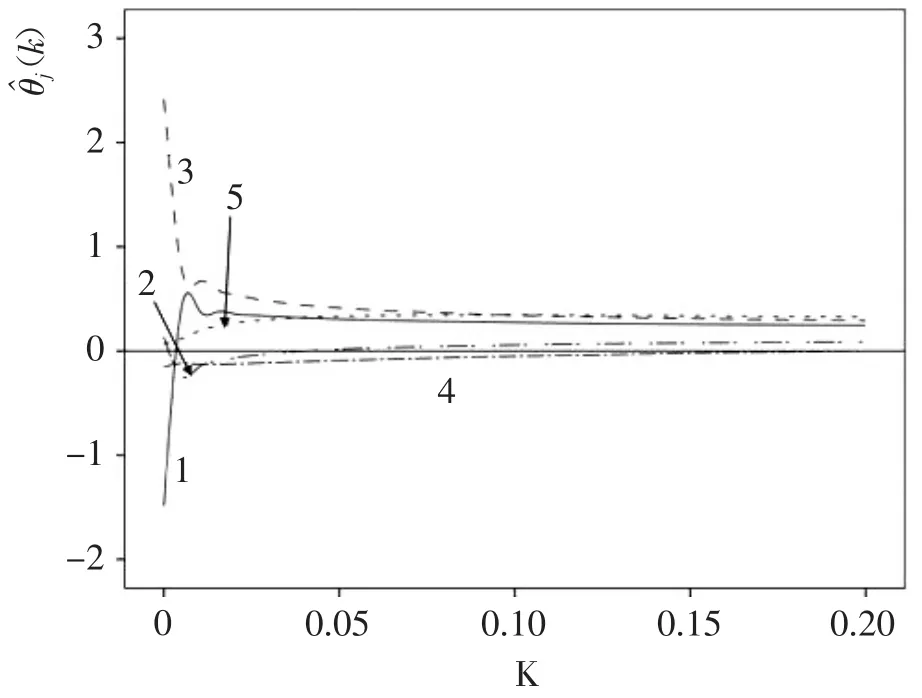
图2 5变量岭迹图

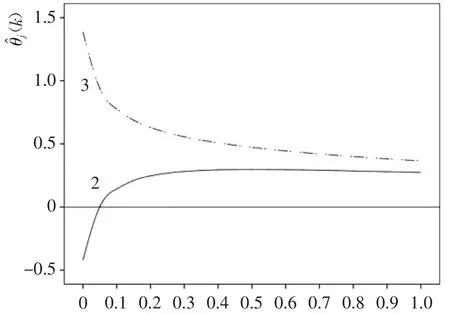
图3 变量X1、X3岭迹图

（三）岭估计

在剔除X1、X4、X5之后，保留变量之间仍存在一定线性关系，计算得X2、X3的OLS回归系数方差膨胀因子接近10，分别为 VIF2=9.55，VIF3=9.55。

故对保留变量进行岭回归分析，通过两变量岭迹来看，当K值达到0.7～0.9的范围时，各个θj（K）（j=2，3）大体上趋于稳定，选取岭参数K=0.8，计算可得岭回归结果（见表 2）。

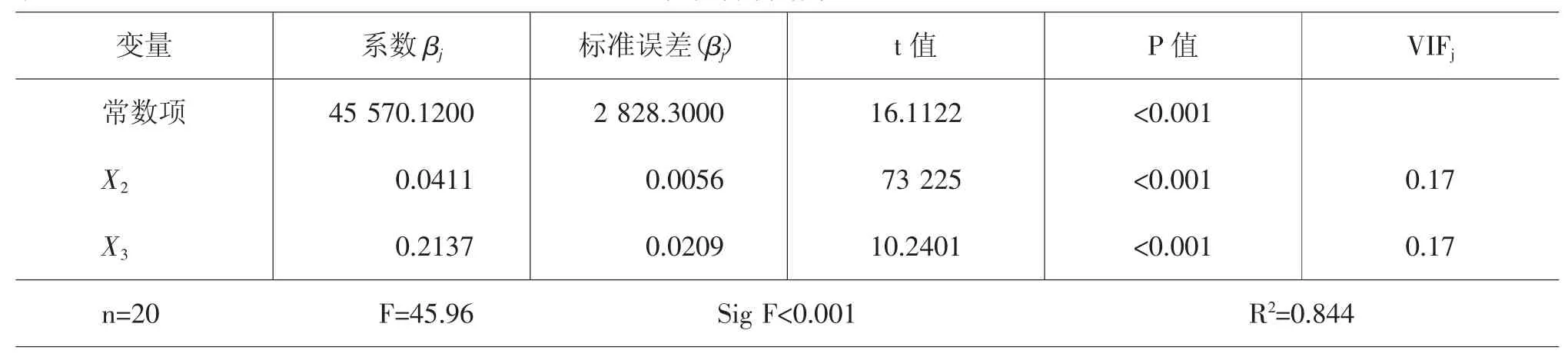
表2 岭回归分析结果（K=0.8）

由表2最终获得岭回归方程:X2、X3系数更加合理。同时，岭回归后各变量的方差膨胀因子极大地降低，VIFj（0.1）＜10（j=2，3），表示非共线性状态。

并且，从表2中结果可知，2预测变量数据变异总和占响应变量变异的84.4%。虽然，该占比不及OLS回归，但岭回归后

（四）误差分析

求得经济数据集的岭回归方程后，将实际总就业人数Y与模型预测值Y^进行对比，可得到该模型平均相对误差（MRE，Mean Relative Error）：

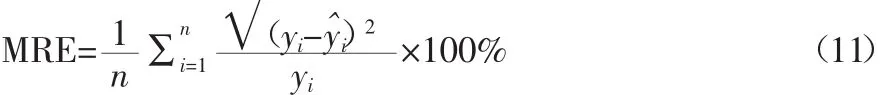
式中，yi为第i个样本的实际值为通过岭回归模型求得对应的预测值。由（11）式求得MRE为0.97%，这意味着基于岭回归建立的模型误差较小，拟合效果较好。

结语

将多元回归模型应用于经济数据时，若该数据集存在多重共线性，OLS无法进行有效的估计和预测，而岭回归方法引入正数K修正OLS正规方程组，通过一种有偏估计方法，消除多重共线性对模型的影响。在实例分析时，首先对宏观经济数据集进行模型假设检验，在模型设定无误情况下，运用变量相关矩阵图、VIF对共线性进行诊断，在确定数据存在严重共线性后，运用岭迹图剔除变量，再进行岭回归。回归结果通过显著性检验且消除了共线性的影响，同时模型误差小，拟合效果较好。

但岭回归参数的选择原则和方法存在一定主观性，没有明确的含义，所以选择变量时需要特别谨慎，要灵活运用岭回归方法，如比较剔除不同变量子集的回归效果。当然，对于共线性问题可根据具体情况采用其他方法，如主成分分析、Lasso 回归[7]等。