增强学习算法在集装箱船舶配载问题上的应用
严翀宇 王男男 沈一帆


集装箱船舶配载是集装箱码头生产作业的重要环节之一,其直接影响码头整体装卸作业效率。目前,我国集装箱码头主要采用传统在线搜索算法解决集装箱船舶配载问题,但此类方法在求解大规模算例时效率较低。为此,本文采用增强学习算法,将大量耗时计算前置到线下训练阶段,实际配载时则利用训练好的网络直接求解,从而提高求解效率。具体思路如下:首先,分析集装箱船舶配载问题的关键决策因素,并从中提炼相关的配载特征向量;然后,根据集装箱船舶配载问题的特点和约束条件,设计相应的状态、动作和回报函数,以计算每组集装箱-船箱位配对的Q值,并以配载特征向量作为网络输入,以每组集装箱-船箱位配对的Q值作为网络输出,以均方误差作为评估函数,构建增强学习网络,并结合Q学习算法实现集装箱船舶配载问题的增强学习算法;最后,分析该算法与传统智能优化算法的区别,说明增强学习算法能够高效求解集装箱船舶配载问题。
1 研究现状
目前,我国集装箱码头主要依靠人工加计算机辅助的方式制订集装箱船舶配载计划,而人工配载的一大弊端是配载结果容易受到配载员个人经验和状态的影响;因此,如何将配载员的个人经验与计算机算法相结合,快速、有效地制订合理的配载计划有重要的研究意义。国内外学者对集装箱船舶配载问题的研究主要集中在配载模型和配载算法方面。
1.1 配载模型的研究现状
(1)主贝计划配载模型 TODD等针对单港口的主贝计划配载问题,以纵倾力矩、横倾力矩、船舶稳性和距离位置等为约束条件,以翻箱量最小为目标函数,采用遗传算法求解。ZHAO等针对集装箱船舶主贝计划配载问题,考虑船舶稳性、翻箱量和场桥作业效率等因素,建立多目标整数规划模型;但该模型过于复杂,很难进行规划求解,缺乏实用性。MOURA等在同时考虑主贝计划和航线因素的情况下,以运输成本最小化为目标函数,建立混合整数规划模型。
(2)贝内计划配载模型 AVRIEL等以翻箱量最小为优化目标构建简单的整数规划模型,并设计相应算法,通过算例验证该算法在较小规模的情况下可以得到较好的求解效果;但该模型过于简单,实用性不强。SHIELDS建立数学模型,并将模型求解结果与实际装船结果进行对比,证明模型的有效性;但由于当时的船舶大多为中小型船舶,该模型已无法适应当前船舶大型化趋势下的约束条件和优化目标。IMAI等构建0-1整数多目标配载模型,计算得到堆场翻箱量;但在配载问题中,如果存在大量0-1整数二元变量和约束条件,求解难度将加大,很难得到最优解。
1.2 配载算法的研究现状
大多数学者采用智能优化算法求解集装箱船舶配载问题。ALVAREZ在考虑正面吊移动距离、翻箱量和船舶质量分布的情况下,提出基于多个初始解的禁忌搜索算法,并将该算法运用到实际算例中与混合整数规划算法进行对比。研究结果表明,其设计的算法能够在较短时间内求解上百个箱量的算例,而混合整数规划算法只能求解40个以内集装箱的算例。KIM等提出运用束搜索算法求解集装箱船舶配载问题,并在考虑场桥和翻箱量等因素的基础上构建模型,制订合理、有效的配载和收箱策略。LEE等利用层级理论解决集装箱船舶配载问题,将发箱顺序问题分解为小规模子问题,并设计一种将蚁群算法与禁忌搜索算法相结合的混合启发式算法。算例验证结果表明,该混合启发式算法的求解效率高于单纯的蚁群算法和禁忌搜索算法。卫家骏[14]设计禁忌搜索-蚁群混合算法求解集装箱船舶配载问题,并通过仿真模拟试验进行验证。
1.3 小结
综上所述,针对集装箱船舶配载问题,现有的研究主要聚焦于构建混合整数规划模型,并利用特殊设计的启发式算法求解。该类算法虽然能够在一定程度上较好地求解小规模算例,但仍然存在很大局限性,例如:只能求解特殊情况下的配载问题;大规模算例的求解效率不高;等等。为此,本文采用增强学习算法,通过训练得到配载智能体,从而能够在各種情况下高效求解配载问题。
2 集装箱船舶配载问题描述
2.1 决策因素
(1)集装箱不悬空原则 在制订装船作业的贝内计划时,需要考虑集装箱的装船顺序。如果同一列的上层船箱位的装船顺序先于下层船箱位的装船顺序,就会造成集装箱悬空现象,致使装船作业无法顺利进行,进而导致装船作业效率下降。
(2)海侧至陆侧装船原则 在陆侧已装船集装箱层高高于海侧已装船集装箱层高的情况下,如果需要继续为海侧船箱位发箱,岸桥的起升高度必须超过陆侧已装船集装箱层高,否则会造成集装箱碰撞。为避免产生上述跨高作业,对于同一层的船箱位,配载时应当考虑从海侧往陆侧实施装船作业,从而确保装船作业的安全性和高效性。
(3)船箱位质量范围原则 在制订贝内计划时,应当考虑主贝计划确定的船舶贝位预分层质量,即每个贝位每层集装箱的质量范围,确保每个船箱位的集装箱质量在此范围内,以满足船舶稳性和集装箱绑扎要求。
(4)重压轻极限原则 理论上,集装箱船舶配载应遵循下重上轻原则;但在实际配载过程中,为方便码头作业,在不影响船舶稳性的前提下,允许存在少量的重压轻。在重压轻的情况下,上下相邻集装箱的质量差通常应控制在0.5~1.0t,具体可根据船型作相应调整。
2.2 优化目标
(1)舱面梯形配载 梯形配载是舱面配载的独特工艺,指配载时应考虑按船箱位顺序从海侧往陆侧以楼梯形式依次发箱,从而确保相邻格栅已装船集装箱的层高不至于相差过大,同时降低岸桥司机的作业难度。
(2)减少翻箱频次 翻箱作业是无用作业,是导致装船作业效率下降的主要因素之一。对于堆场内同一箱区、同一贝位、同一列的集装箱,配载时应尽量使上层集装箱先发,否则会导致翻箱作业。为避免场桥频繁翻箱,配载时应当考虑同一箱区、同一贝位、同一列的集装箱从上往下依次发箱,从而使场桥翻箱频次最小。
(3)减少移机频次 此处的移机指场桥在不同箱区之间或同一箱区内的不同贝位之间移动。装船作业时,如果相邻发箱顺序号所对应的集装箱位于不同箱区或同一箱区内的不同贝位,就会造成移机。不合理的发箱顺序会导致场桥在不同箱区之间或同一箱区内的不同贝位之间频繁移动,使得装船作业效率下降;因此,配载时应当考虑同一箱区内的同一贝位连续发箱,从而使场桥移机频次最小。
3 集装箱船舶配载问题增强学习算法设计
3.1 增强学习算法概述
设计函数Q(s,a),用于计算配载状态s下执行
式中t为时刻;st为系统在时刻t的状态;at为决策者在系统处于状态st的情况下所采取的动作;rt为系统在状态st下通过动作at获得的回报值。
式中:t为时刻;st为系统在时刻t的状态;at为决策者在系统处于状态st的情况下所采取的动作。
3.2.2 配载状态设计
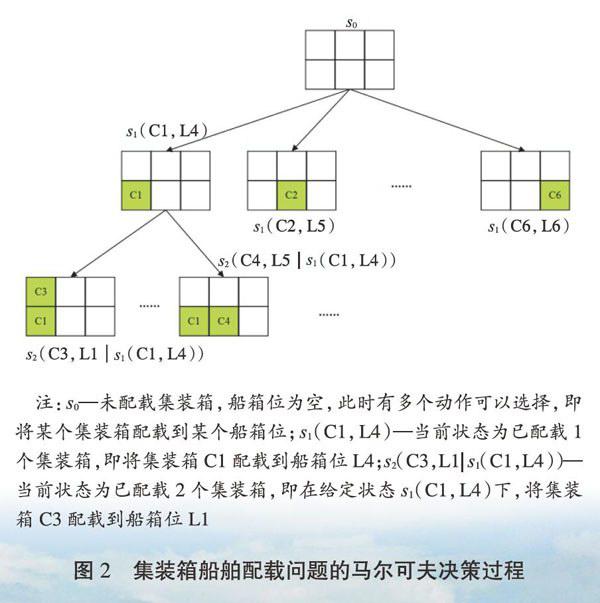
在配载问题中,t为配载顺序,t=0表示未配载集装箱,t=1表示配载第1个集装箱,t=2表示配载第2个集装箱,以此类推。假设船箱位序号为L1~L6(见图1),则集装箱船舶配载问题的马尔可夫决策过程如图2所示。
配载动作a所得到的总回报值。在初始阶段,配载智能体就像一位对集装箱船舶配载问题一窍不通的配载员。针对配载智能体为解决配载问题所采取的每个配载动作,即集装箱-船箱位的配对,回报函数均会反馈相应的回报值。配载智能体通过这一反馈来更新函数Q(s,a),并根据更新后的函数Q(s,a)决策下一个配载动作,这就是增强学习的迭代过程。配载智能体通过不断地试错,从中吸取经验,逐渐学会在特定状态下如何配载才能获得最大回报值,最终使配载问题的评价迭代收敛到最优。
3.2 集装箱船舶配载问题的马尔可夫决策过程
3.2.1 马尔可夫决策过程概述
马尔可夫决策过程可表述为:在系统处于某个状态的情况下,决策者的决策决定其所采取的动作,该动作决定系统获得的回报值和下一时刻系统将达到的状态。马尔可夫决策过程的数学表达式为
马尔可夫决策过程具有无后效性,即系统获得的回报值以及系统从当前状态向下一状态转移的概率只取决于当前状态和动作,而与历史状态和动作无关。状态转移函数
注:s0一未配载集装箱,船箱位为空,此时有多个动作可以选择,即将某个集装箱配载到某个船箱位;s1(C1,L4)—当前状态为已配载1个集装箱,即将集装箱C1配载到船箱位L4;s2(C3,Ll∣s1(C1,L4))—当前状态为已配载2个集装箱,即在给定状态s1(C1,L4)下,将集装箱C3配载到船箱位L1
3.2.3 配载动作设计
在配载问题中,动作定义为集装箱与船箱位的配对,即将某个集装箱配载到某个船箱位。以图2为例,若不考虑配载约束条件,配载状态s0下可执行的配载动作有36种,即集装箱与船箱位的配对方式有36种。
3.2.4 配载回报设计
集装箱船舶配载问题中的回报函数设计与各个目标函数的权重以及约束条件有关。配载效果的评价指标主要包括配载完成情况、翻箱情况、移机情况、重压轻情况等。鉴于上述指标在配载过程中的重要程度不同,设计回报函数时有不同的侧重。
式(3)~(5)分别表示配载完成情况回报值、翻箱情况回报值和移机情况回报值。
3.2.5 配载值函数和动作价值函数设计
设计配载值函数和动作价值函数,即
式(10)表示所选取的在场箱的质量;式(11)表示所选取的在场箱所在船箱位的层高;式(12)表示所采取的配载动作中的集装箱与其所在船箱位下方集装箱的质量差;式(13)表示所采取的配载动作的潜力值,即在将该配载动作作为本次配载策略的情况下,比该配载动作中的集装箱质量轻的集装箱数量与该集装箱所在船箱位上方空余船箱位数量之差,也就是当前配载动作对该配载动作中的船箱位上方集装箱配载的影响情况;式(14)表示所采取的配载动作产生的堆场翻箱量;式(15)表示所采取的配载动作中的集装箱的发箱顺序与其左侧集装箱所
式(6)~(9)中: π为所选择的配载策略;λ为下次配载对于当前配载的影响因子;T(s∣s,a)为从配载状态s采取配载动作a最终到达配载状态s的概率;R(s∣s,a)为从配载状态s采取配载动作a最终到达配载状态,所获得的回报值;v(s)为在配载状态s下采取配载动作a所获得的期望回报值,即在该船箱位配载该集装箱将给之后配载其他集装箱带来的回报值;Q(s,a)为在配载状态s下采取配载动作a所获得的总回报值;V*(s)为在配载状态s下可获得的最大回报值;V*(s,a)为在配载状态s下采取配载动作a所获得的最大回报值。
3.3 配载特征分析
为解决维度灾难问题,本文用配载问题的9个相关特征近似表示配载状态。以下描述的特征均针对当前配载状态可能采取的配载动作进行说明。假设每个配载动作的特征向量为
属区位的发箱顺序差;式(16)表示所采取的配载动作中的集装箱的发箱顺序与其下方集装箱所属区位的发箱顺序差;式(17)表示所采取的配载动作中的集装箱是否从同区位发出;式(18)表示所采取的配载动作中的集装箱是否与其前一配载动作中的集装箱从同区位发出。
4 增强学习算法求解集装箱船舶配载问题的优势
(1)计算迁移 传统智能算法聚焦于问题的决策阶段,需要花费大量时间对问题进行求解计算。对于超大型集装箱船舶而言,为获得较好的配载结果,采用传统智能算法通常要比人工配载花费更多时间。与传统智能算法不同的是,增强学习算法聚焦于問题的学习阶段,可以在任何时间段学习配载数据,从而将大量的计算迁移至学习阶段,在决策阶段则直接使用增强学习得到的参数集进行求解;因此,增强学习算法的求解效率较高,通常可在1s内计算上千个集装箱的配载结果。
(2)泛化能力强 传统智能算法通常需要人工提炼各种配载规则并划定问题边界,并在对各种规则和问题模型化的基础上求解;因此,传统智能算法对规则和边界以外的配载问题往往难以取得较好的结果。增强学习算法则基于历史数据学习各种配载情况,使得配载智能体能够掌握隐藏在数据背后的规律,即使面对全新的配载样本也具备较强的适应能力。
5 结束语
本文采用增强学习算法求解集装箱船舶配载问题,其主要创新点如下。
(1)运用机器学习的相关理论和方法求解规划模型,将大量的计算迁移到模型训练学习阶段,从而大幅提高决策阶段的计算效率。
(2)将配载问题的目标和约束条件转换为特征向量,使配载智能体通过增强学习从特征向量中自动提取不同状态下的配载策略,从而避免传统启发式算法下因人工设计启发规则而造成的有偏估计。
(3)相关研究思路和方法对解决集装箱码头场地计划、场桥调度、智能收箱等问题具有一定的借鉴意义。
参考文献:
[14]卫家骏.混合蚁群算法求解集装箱箱位分配问题[J].中国航海,2011,34(2):96-100.

