基于能量理论的手绳打结研究

张冬冬董一嘉黄松檀吕俊杰杨惠杰应富强

(1.浙江机电职业技术学院 机械技术系，浙江 杭州 310053；2.浙江工业大学 机械工程学院，浙江 杭州 310014；3.中国联合工程有限公司 装备工程公司，浙江 杭州 310052)

0 引 言

目前，服装行业的打结依旧是人工打死扣的方式，劳动强度大、效率低。现在的打结装置大都是打结器，如农业方面用于秸秆捆扎D型打结器，手术行业用于外科手术缝合的丝线打结器等，因此，对服装行业的打结装置进行设计研究具有一定的科研和市场价值。而在研究手绳打结过程中，拎手绳的能量分析是实现高成结率的重要一环。

国内外学者对打结开展了大量研究，中国农业大学的张安琪博士[1-2]分析了打结器割绳脱扣机构空间结构参数，研究了打结器运动图像与捆绳张力信息同步获取系统；李海涛教授[3-4]对割绳脱扣机构进行了磨损分析与改进设计；陈龙健教授[5]基于逆向工程技术对D型打结器进行了三维重构与运动仿真、打结钳嘴载荷试验分析[6]；江苏大学的尹建军研究员[7-9]运用刚柔接触动力学研究了打结器虚拟打结方法，设计了双齿盘驱动打结器，进行了成结试验分析、动作参数分析和打结试验；哈尔滨工业大学的李哲教授[10]建立了海带悬链线数学模型，通过将海带线在4种状态下的空间曲线向指定平面投影的方法证明扭转打结法的可行性；天津大学岳龙旺等[11]设计了虚拟血管缝合系统，建立了缝合线力学模型；PHILLIPS J等[12]采用有自适应功能的弹簧质点模型来对绳子进行了模拟打结。上述研究着重于运动仿真、动作功能、结构性能分析及空间结构参数分析等，并未从能量角度分析打结过程中绳子状态来指导打结装置的设计。

本文将根据手工打结的原理，利用能量理论分析打结过程中不同阶段手绳的状态，研制手绳打结装置，并进行稳定性实验。

1 手绳数学模型

手绳手工打结方式如图1所示。

图1 手绳打结方式

笔者通过手工打结的原理，来建立手绳数学模型。

从微分思想出发，任意取手绳的微小段，绳微端的一端拉力为T1，另一端拉力为T2，手绳的线密度为ρ，受到重力为ρgΔl。

手绳微段受力如图2所示。

图2 手绳微段受力

由物体受力平衡条件可得：

(1)

式中：T1H—下端拉力X轴分量；T1V—下端拉力Y轴分量；T1W—下端拉力Z轴分量；T2H—上端拉力X轴分量；T2V—上端拉力Y轴分量；T2W—上端拉力Z轴分量。

由图2可看出：绳的张力在X和Z轴方向上的分量是相等的，而在Y轴方向上的分量是随着x和z的变化而变化，设Y轴方向上的分量为T(x,z)，根据式(1)可得：

T(x+Δx,z+Δz)=T(x,z)+ρgΔl

(2)

(3)

(4)

由一阶导数的几何意义可知：

(5)

由图1可得：

(6)

联立式(4～6)得：

(7)

由T(x)=T2H×f′(x)，可推出：

T′(x)=T2H×f″(x)

(8)

联立式(7,8)可得：

(9)

设a=T2H/ρg，可解得：

(10)

式中：a—悬链系数；c1，c2—任意常量。

式(10)为手绳的数学模型。

2 手绳的能量

在打结过程中，绳圈的稳定直接影响打结的成功率，而绳圈的稳定关系比较大的往往是其自身的稳定。由能量理论可知：能量总是由高能量状态向低能量状态转变，所以稳定的绳圈就是其处于低能量状态；而高能量状态的绳圈会有向低能量状态的绳圈自动转变的趋势，在高能量向低能量转变过程中容易导致绳圈发生不利于稳定的不规则变形，从而提高成结难度。

本文分析手绳的绳圈能量从悬挂约束下的拎手绳的重力势能、缠绕成圈中的弯曲能量Eb和成结中的扭转能量Et着手。

2.1 手绳的重力势能

手绳的势能通常分为重力势能和弹性势能[13]。在手绳悬挂约束待打结状态下，前者占主导地位，因为绳子没有张紧，形变很小，弹性势能很小，可以不考虑。

根据上文拎手绳数学模型来分析拎手绳重力势能的最小空间状态，本研究取悬挂约束到缠绕到170°过程中的某一状态为例进行定量分析，在这一状态下两端固定，手绳缠绕示意图如图3所示。

图3 手绳缠绕示意图

A(x1,y1)，B(x2,y2)两点为手绳缠绕过程中的两定点。其中：A点是圆周的四等分点，B点是另一固定点。设经过这两点的曲线y=f(x)的长度为L，该段曲线的重心坐标为(x,y)，那么由弧长公式可得：

(11)

由重心公式可得：

(12)

因为讨论的是手绳的重力势能只与重心的高低有关，只需考虑y0的大小即可，这样设泛函J(y)为：

(13)

(14)

(15)

把式(15)代入式(14)，得：

1+(y′)2-y*y″=0

(16)

解式(16)微分方程得：

(17)

式中：a，c—常数，由以上各式的推导过程可知。

从引入欧拉拉格朗日方程，每一步推导都是在临界状态下进行，从而反证出，过两定点的曲线中，悬链线的重心最低，即悬链线的势能最小。

由图3可知：在缠绕到170°的过程中重力势能占主导地位，再由上述推导得悬链线的势能最小，所以按悬链线缠绕方式的拎手绳能量最低，最稳定。

2.2 手绳的弯曲能量

根据打结过程，第二阶段是成绳圈，即绳弯曲成圈的过程，所以本研究考虑手绳的绳圈弯曲能量，对手绳进行简化分析，将手绳投影到二维平面为一曲线。

设该手绳投影曲线r=r(s)，其中s是弧长，平面曲线向量分布如图4所示。

图4 平面曲线向量分布

曲线可表示为：

r(s)=(x(s),y(s))

(18)

因此，可以计算出其单位切向量：

α(s)=r′(s)=(x′(s),y′(s))

(19)

在此向量平面中，有且仅有一个与α(s)垂直的正交的单位向量，即：

β(s)=(-y′(s),x′(s))

(20)

由单位正交向量知识可知：α(s)是单位向量，存在与其正交的单位向量α′(s)，使得α(s)⊥α′(s)。从而平面曲线r=r(s)的相对曲率可计算得：

α′(s)=κrβ(s)⟹κr=α′(s)·β(s)

(21)

由以上推导可知，手绳二维平面曲线的Frenet公式为[14]：

(22)

其中，α(s)与x轴的正向夹角记作θ(s)，θ(s)为α(s)切向量，同样也为α(s)的方向角。这时α(s)可表示为：

α(s)=(cosθ(s),sinθ(s))

(23)

联立式(18，20)，可得：

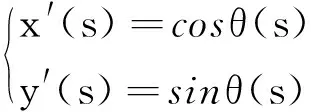
(24)

对式(24)再次求导，可得：

(25)

其中，α′(s)=(x″(s),y″(s))。则：

α′(s)=(x″(s),y″(s))=(-sinθ′(s)·θ′(s),
cosθ′(s)·θ′(s))

(26)

式(26)两边点乘β(s)，联合式(20，23～25)，可得：

α′(s)·β(s)=(-sinθ′(s)·θ′(s),cosθ′(s)·θ′(s))·
β(s)=(sin2θ′(s)+cos2θ′(s))·θ′(s)=θ′(s)=κr

(27)

手绳打结过程中弯曲成绳圈时要保持稳定状态，即低能量状态，需符合能量最小原则。由MOLL M等[15]对能量最小原则研究方法的研究结果可知：弯曲状态下的曲线会产生方向角θ(s)，可以通过每一微段的方向角θ(s)来判断手绳二维平面的曲线形状。所以本研究将手绳等长度均分，记每一等分段为手绳的单位长度，分析每一等分段的方向角。

手绳在二维平面投影的曲线弯曲示意图如图5所示。

图5 手绳弯曲示意图

由文献[16]可知绳圈的单位弯曲能量公式：

(28)

式中：Eb—弯曲能量；Kb—弯曲刚度；c(s)—曲率，即κr。

通过联立式(27，28)可计算得到曲线的单位弯曲能量：

Kbθ′(s)1θ′(s)2

(29)

当且仅当θ′(s)1=θ′(s)2时，有：Eb(min)=Kbθ′(s)1θ′(s)2。

对θ′(s)1=θ′(s)2两边积分，可得：

(30)

计算时，手绳曲线的方向角设为0，将θ(s)0=0将带入式(30)，可得：当且仅当方向角θ(s)1=θ(s)2时，手绳曲线的等分段弯曲能量最小，这时手绳处于低能量状态，其较为稳定。由此可得：曲线弯曲的形状趋于圆形时，手绳弯曲能量最小，最稳定。

在缠绕成绳圈的过程中，即缠绕170°到400°之间(角度从试验中测得)，在此过程中，绳子的重心变化小，所以重力势能较小，弯曲能量占主导地位。由式(28)可知：该阶段影响能量的主要因素是缠绕时绳圈的曲率。

2.3 手绳的扭转能量

分析打结过程中，手绳绳圈扭转能量前，本研究做一个手动实验进行直观演示。

绳圈扭转实例如图6所示。

图6 绳圈扭转实例

用双手将绳子伸直，该情况下，Lk=Tw=0(其中，Lk—环绕数，Tw—扭转数)，绳子产生的能量为0，如图6(a)所示。

双手用力将实验用绳子自身产生扭转并拉直，此时，指尖明显能感觉到绳两端有想复原较大扭力，而且如果对绳扭转越多，反抗的扭矩也越大，手指不跟着增加力道容易使得绳脱落，这时环绕数和扭转数都大于1，如图6(b)所示。

继续增加绳的扭转数后，放掉两手横向伸直力，绳就变成缠绕麻花状如图6(c)所示。在增加扭转数过程中，绳自身的抵抗能量，即扭转能量，越来越大。

通过手工扭转绳子实验可得，绳圈的扭转数是产生绳圈扭转能量的主要影响因素，所以分析绳圈能量时，对绳圈的扭转能量通过扭转能量公式进行分析[17]：

(31)

式中：Et—扭转能量；Kt—扭转刚度；Tw—扭转数；L—绳子长度。

最后成结阶段，绳圈已不需再缠绕弯曲且重心不变，所以弯曲能量和重力势能不变。一绳端移动另一端固定使得绳自身开始绷紧，使得绳自身为摆脱绷紧有扭转趋势，所以在成结阶段扭转能量占主导地位。

由式(31)可知：Kt和L是绳子材料的固有属性都为不变量，所以在成结阶段影响能量的主要因素是扭转数Tw。绳子的扭转数越少有利于稳定快速成结。

3 打结试验

为了验证上述理论分析，试验在手绳打结装置平台上进行，该试验平台由绕绳机构、传动机构、成结机构及控制部分组成，控制部分为步进电机，调速由外接的调速控制器来实现。

手绳打结装置样机如图7所示。

5.3 mm直径的手绳打结实验过程如图8所示。

图8 5.3 mm直径的手绳打结实验过程①移动轴；②手绳；③绕绳部分

5.3 mm拎手绳由绕绳机构从0°旋转到170°之间，绳子的重力势能起主要作用，所以拎手绳在旋转到170°之前，投影到二维平面，符合悬链线方程，其势能最小。在170°～400°，用于打结部分的绳段接近于圆，这阶段弯曲能量起主要阻碍作用。最后成结过程中，绳子的自身扭转起主要阻碍作用，自身的扭转数越少，越容易成结。

由于一次实验成功不足以说明成结稳定性，本文又进行鲁棒性试验。实验过程如图9所示。

针对不同直径的手绳进行的打结实验统计结果如表1所示。

表1 不同直径的手绳打结实验结果

由实验结果可知:成绳圈过程中是沿着移动轴外表面缠绕，所以轴表面应有一定摩擦力，也就是对移动轴表面做一些改进，增加其阻碍绳子移动的力度，这样成绳圈就容易，弯曲能量就低。从图9(a,e)可以看出：在成结阶段由于绳直径相对于凹槽过大或者过小都无法成结，尤其直径大于6 mm的拎手绳成圈所需拉力大，产生的弯曲能量也大，成结越困难。直径小于2 mm的拎手绳，在成结阶段，由于凹槽直径大于拎手绳直径，无法带动拎手绳成结；拎手绳直径对打结成功率影响较大，打结失败都是发生在最后的成结的过程中，直径越大的拎手绳在成结过程中越能抵抗自身的运动，也就是扭转能量越大，打结越容易失败。本文的打结实验装置对于直径在2.8 mm到5.3 mm之间的拎手绳打结成功率具有一定稳定性。

由上述知：整个打结过程分为待打结、绕绳圈及成结，且3个阶段的主导能量分别为重力势能、弯曲能量及扭转能量。通过对绳段进行受力分析，待打结状态下手绳只受重力势能，解微分方程得到悬链线状态下手绳处于最低重力势能，所以实验过程中先使待打结的手绳悬垂接近悬链线状态；对绕绳过程中手绳的绳端进行分析，得到绳圈越接近圆其弯曲能量越小，所以试验过程中手绳绕着圆轴形成绳圈；根据扭转能量公式得绳子自身的扭转数越少扭转能量就越小，于是最后成结阶段不用特别考虑能量只需成结速度快。

4 结束语

本文根据手工打结的原理，利用能量理论分析了打结过程中不同阶段手绳的状态，研制了手绳打结装置，并进行了稳定性实验。

本文后续的研究为：完成到移动轴带动绳端成结的过程的三维数学模型，研究缠绕速度与能量的关系，实现实时打结，研究最优打结轨迹及打结过程中绳子的张力大小、摆动幅度及绳端的跨度。