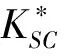基于模型约束逆建模的储层物性参数估计方法

刘 倩， 董 宁， 季玉新， 陈天胜

(中国石油化工股份有限公司 石油勘探开发研究院，北京 100083)

0 前言

储层物性参数是了解油气储层的物理特性和几何特性的必备要素，因此将储层弹性参数转换为储层物性参数的方法一直是储层地球物理的研究热点之一。最简单、也是早期储层物性参数估计中常用的策略是基于统计学理论建立弹性参数(速度、密度、阻抗等)和物性参数之间的经验关系实现物性参数的间接估计[1-4]。

对于复杂的储层而言，简单的统计拟合得到的经验关系不足以准确描述弹性参数和物性参数之间的复杂关系。岩石物理模型作为连接储层的弹性性质与物理性质的纽带，被越来越多地应用于储层物性特征的描述中。针对不同岩石的矿物组成、孔隙类型等物理性质，学者们建立了不同的岩石物理模型。Voigt - Reuss - Hill模型和Hashin-Shtrikman-Walton模型建立了矿物的弹性性质与岩石基质的弹性性质之间的关系[5-6]；接触模型(CT模型)和接触胶结模型(CCT模型)可以用于计算高孔隙或弱胶结的岩石的弹性性质[7-9]；Kuster-Toksöz模型、微分等效介质模型(DEM模型)和自相容近似模型(SC模型)可以用于胶结程度较强的岩石的弹性性质的研究[10-13]。

岩石物理建模理论的发展推动了储层物性参数估计技术的发展。Mukerji等[14]和Eidsvik等[15]基于信息论提出了统计岩石物理方法来反演储层物性参数；Bachrach等[16]综合运用岩石物理随机建模方法和贝叶斯反演理论来反演孔隙度和含水饱和度；Yin等[17]建立了基于FFT-MA模拟方法和GDM扰动方法的地质统计学物性参数反演方法；Alvarez等[18]基于岩石物理理论提出了多属性旋转技术来估计储层物性参数；Gui等[19]基于贝叶斯反演框架建立了弹性参数加权统计的储层物性参数反演方法；李志勇等[20]利用叠前地震同步反演来实现储层物性参数和弹性参数的同步预测；Boateng等[21]基于Caianiello神经网络算法和Levenberg-Marquardt最优化算法提出了高精度的孔隙度反演方法。

笔者以岩石物理理论为基础，在三维储层参数域进行岩石物理建模，选取三种弹性参数作为输入数据，计算出弹性参数在储层参数域的等值面，利用三个等值面的空间交会，在模型约束条件下同时估计出孔隙度、泥质含量和含水饱和度三种储层物性参数。通过模型实验和实际工区应用实例，检验了方法的有效性和实用性。

1 方法原理

岩石物理模型建立了储层物性参数和弹性参数的联系，这种联系是储层物性参数估计的基础，因此根据目标储层的性质建立合理、准确的岩石物理模型是准确估计物性参数的前提[23]。

建立岩石物理模型[24]，建模过程中的基本参数如表1所示。

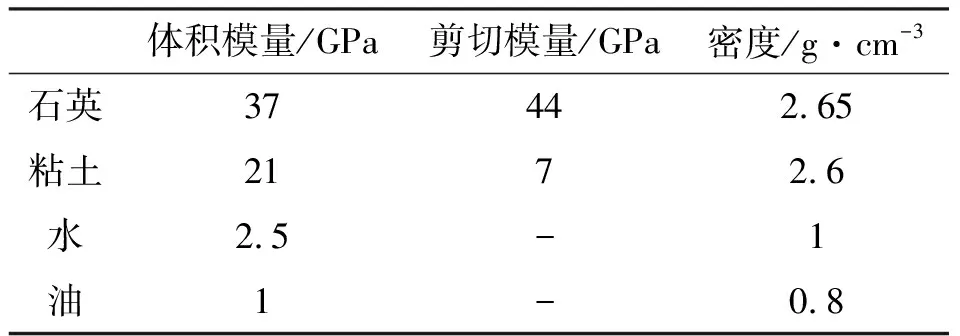
表1 基本组分参数表

储层特征描述最常用的参数是孔隙度φ、含水饱和度Sw和泥质含量Vsh，建立一个三维直角坐标系，分别以Vsh、φ、Sw作为x、y和z轴，坐标轴的范围分别是0～1、0～0.4和0～1，各坐标轴均匀采样，该坐标系称为一个储层参数域。在这个储层参数域中，每个点的坐标就是一组储层物性参数，根据岩石物理模型正演方法计算弹性参数值，并在整个参数域内对弹性参数进行插值就建立了弹性参数的三维数据体d。

图1 储层参数域的弹性参数数据体图Fig.1 Elastic parameter data cube in reservoir parameter domain

图1是体积模量的三维数据体，根据相同的原理可以建立剪切模量和密度的三维数据体。已知地下储层中某点的实测弹性参数数据d0(K0,μ0,ρ0,λ0,σ0)，要同时进行三种物性参数的估计需要至少有三种弹性参数，可以根据储层特点灵活选取弹性参数种类(如体积模量K0、剪切模量μ0和密度ρ0)。

采用Marching Cubes算法分别在体积模量、剪切模量和密度的数据体中计算出值为K0、μ0和ρ0的等值面[23]。在等值面的拓扑结构比较简单的情况下，经典的Marching Cubes算法就可以完成；在等值面的空间构型较为复杂情况下，需要使用改进的Marching Cubes算法[25]，以保证曲面拟合的精度和效率。

如图2(a)是值为K0的体积模量的等值面图，该等值面可以用SK0(Vsh,φ,Sw)表示。同理可以得到密度在储层参数域的等值面Sρ0(Vsh,φ,Sw)，将等值面SK0(Vsh,φ,Sw)和等值面Sρ0(Vsh,φ,Sw)交会在同一个储层参数域中，即可找到同时满足体积模量为K0和密度值为ρ0的点，如图2(b)所示，这些点就分布在两个等值面的交线lK0 ρ0上。

为了得到交线上各点的坐标，建立如方程(1)的目标函数，在两个等值面的定义域交集内求取目标函数的最小值。

J1=‖SK0-Sρ0‖2

(1)

其中：SK0、Sρ0是等值面SK0(Vsh,φ,Sw)和Sρ0(Vsh,φ,Sw)内的所有点。

作为输入数据的弹性参数通常是地震反演的结果或者测井数据重构的结果，因此其中通常包含一定的误差。为了提高算法的稳定性、减少输入数据的误差对估计结果精度的影响，在方程(1)加入模型约束项，目标函数变为式(2)。

‖Sρ0-m‖2

(2)

图2 储层参数域的等值面图及其交会图Fig.2 Isosurfaces and intersection of isosurfaces in reservoir parameter domain(a)体积模量等值面图；(b)两个等值面的交会图；(c)交线与剪切模量等值面的交会图

其中，在井位置处m是实际测井测得的储层物性参数，作为模型约束；在井旁道的位置没有测井数据，可以利用井间插值、地质统计学建模等方法建立的模型作为m进行约束。

计算出剪切模量为μ0在储层参数域的等值面Sμ0(Vsh,φ,Sw)，将其与图2(b)中的两个等值面的交线交会在一起，结果如图2(c)所示。图2(c)中交线与等值面的交集部分是图中黑色圆圈标出的点，这个点的体积模量为K0、剪切模量为μ0和密度为ρ0，则这个点的坐标就对应要估计的储层物性参数。

建立如方程(3)的目标函数，同样加入模型约束项。利用最优化算法在交线lK0 ρ0与等值面Sρ0的定义域交集内求取目标函数的最小值即可得到交点的坐标(0.20,0.30,0.49)。

J3= ‖LK0 ρ0-Sμ0‖2+ ‖LK0 ρ0-m‖2+

‖Sμ0-m‖2

(3)

其中:Sμ0是等值面Sμ0(Vsh,φ,Sw)内的所有点；LK0 ρ0是等值面SK0(Vsh,φ,Sw)和Sρ0(Vsh,φ,Sw)的交线上的所有点。

2 模型试算

2.1 抗噪性分析

为了检验本文提出的储层物性参数估计方法的有效性，建立一个包含27个点的储层物性参数模型，其孔隙度、泥质含量和含水饱和度数据如图3所示。将这些模型数据与表1中的基本参数结合，利用参考文献[20]中的岩石物理建模方法计算出一系列弹性参数：体积模量K、泊松比σ、密度ρ、拉梅参数λ和μ、纵波阻抗IP、横波阻抗IS、杨氏模量E等。这里选取体积模量K、泊松比σ和密度ρ作为输入数据进行储层物性参数估计，结果如图4所示。图4中的黑色圆圈是模型数据，绿色实心点是估计结果，通过对比可知，估计结果与模型数据基本一致。

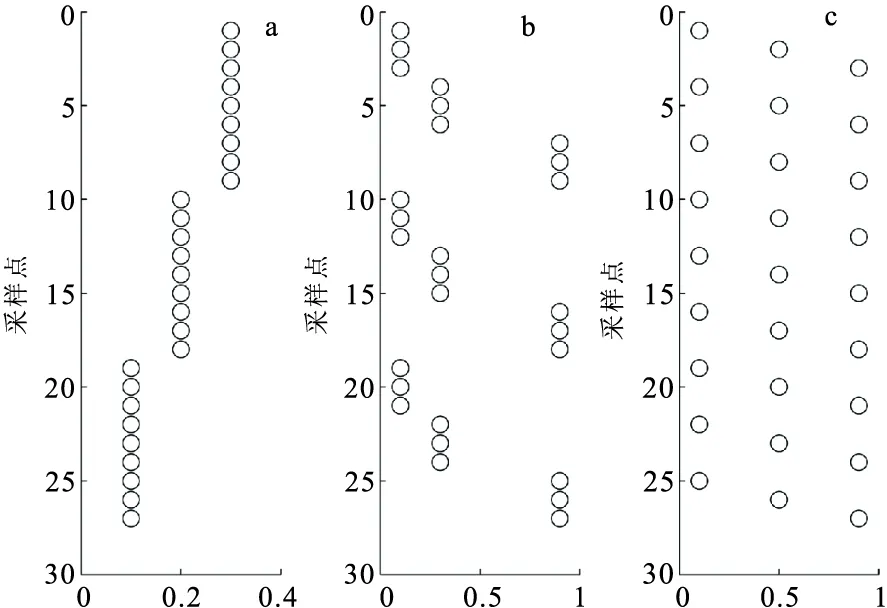
图3 原始模型Fig.3 Original model(a)孔隙度;(b)泥质含量;(c)含水饱和度

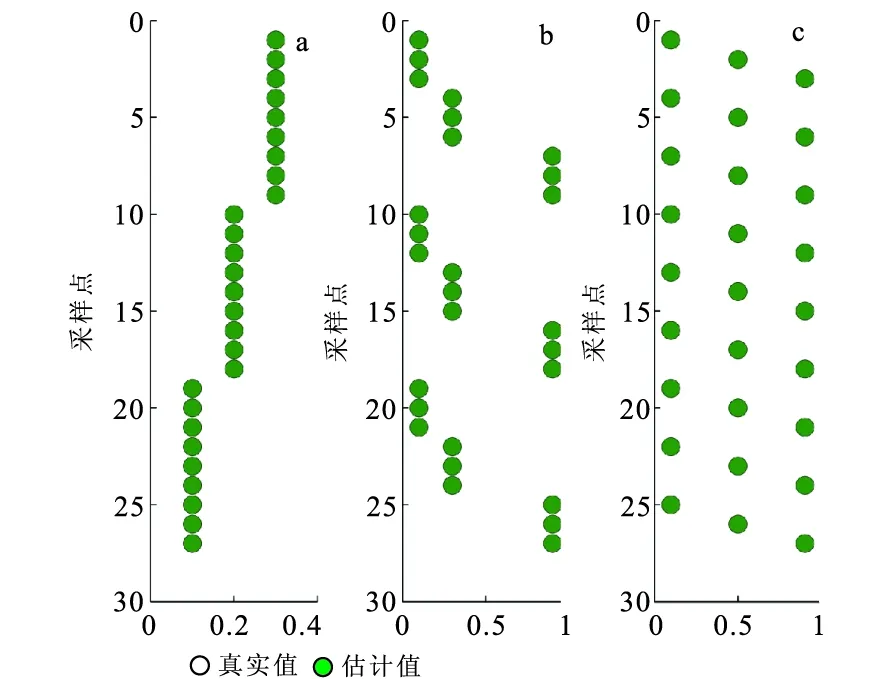
图4 估计结果与原始模型的对比Fig.4 Comparison of estimations and original data(a)孔隙度；(b)泥质含量；(c)含水饱和度

实际数据(测井数据、地震数据、反演结果)都包含一定的噪音或者误差。因此实际应用中，物性参数的估计过程会受到输入数据误差的影响。为了检验该方法的稳定性，在输入数据体积模量K、泊松比σ和密度ρ中均加入8%的扰动，用于模拟包含误差的输入数据，然后分别进行无约束和有约束的估计。由图5～图7可以看出，有约束情况下的估计误差远小于无约束情况的估计误差，证明了加入约束的必要性和有效性。

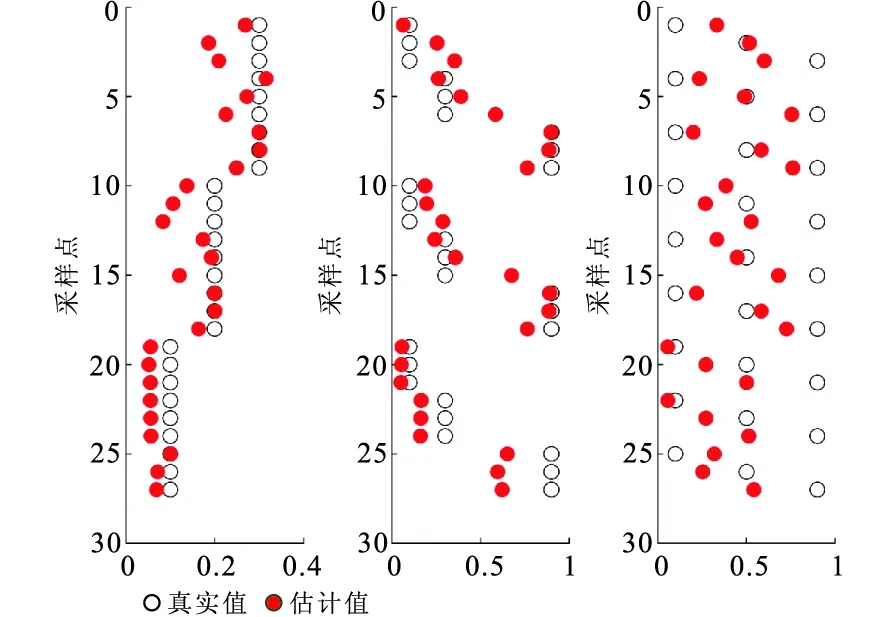
图5 加入扰动后的无约束估计结果 与原始模型的对比Fig.5 Comparison of unconstrained estimations with perturbation and original data(a)孔隙度；(b)泥质含量；(c)含水饱和度

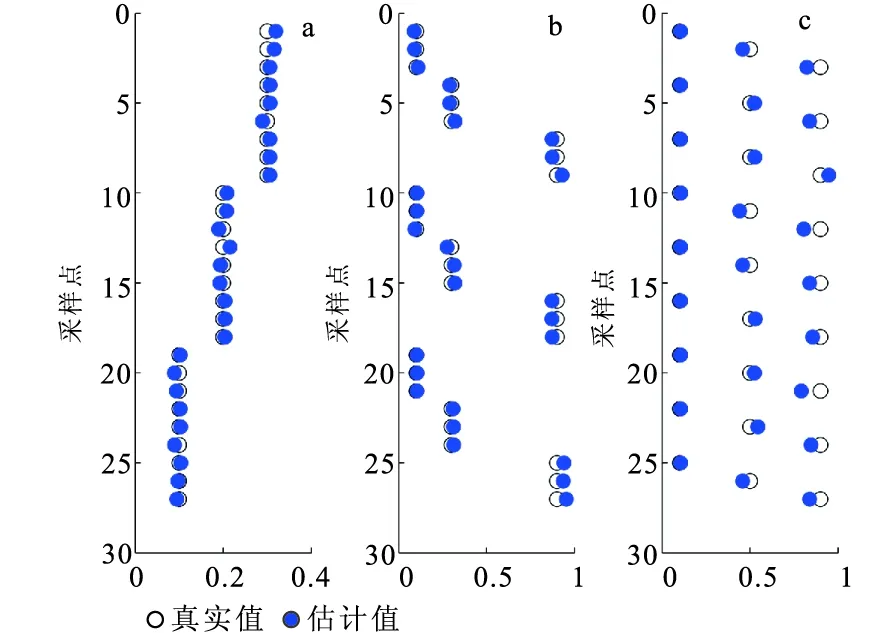
图6 加入扰动后的有约束估计结果 与原始模型的对比Fig.6 Comparison of constrained estimations with perturbation and original data(a)孔隙度；(b)泥质含量；(c)含水饱和度

图7 有扰动情况下有、无约束估计结果 的相对误差绝对值对比Fig.7 Relative error comparison of constrained and unconstrained estimations with perturbation(a)孔隙度；(b)泥质含量；(c)含水饱和度

图8 不同的输入数据扰动引起的估计结果 的相对误差绝对值对比Fig.8 Comparison of relative estimations errors from input data with different perturbations(a)孔隙度；(b)泥质含量；(c)含水饱和度

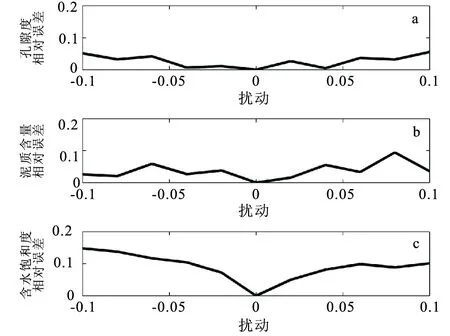
图9 不同扰动情况下的估计结果的相对误差绝对值Fig.9 Comparison of relative estimations errors from input data with different perturbations(a)孔隙度；(b)泥质含量；(c)含水饱和度

为了进一步检验本文方法的稳定性，在输入数据中加入不同程度的扰动，加入的扰动包含如下三种情况：①体积模量8%，泊松比0%，密度0%；②体积模量0%，泊松比8%，密度0%；③体积模量0%，泊松比0%，密度8%；④体积模量8%，泊松比8%，密度8%。在这四种情况下分别进行物性参数估计，得到的结果如图8所示。由图8可以看出，前三种情况得到的估计结果精度接近，第四种情况误差最大，而孔隙度和泥质含量的估计结果中第①种情况的结果略好。综合四种情况而言，孔隙度和泥质含量的误差小于含水饱和度的误差。

在输入数据体积模量、泊松比和密度中加入相等的扰动，扰动范围是-8%到8%。利用有扰动的输入数据进行有约束估计，然后将27个点的估计结果按照输入数据扰动大小分别取平均值。图9是估计结果的相对误差的绝对值随着扰动变化的变化图。从图9中可以看出，孔隙度受扰动影响最小，含水饱和度受扰动影响最大，且扰动绝对值越大，三种储层物性参数的估计结果的误差越大。

2.2 岩石物理模型的影响

为了研究不同的岩石物理模型对于储层物性参数估计结果的影响，分别用微分等效介质模型(DEM模型，见附录)和自相容近似模型(SC模型，见附录)进行实验。

利用Xu-White模型、DEM模型和SC模型计算图4中的数据得到体积模量、泊松比和密度作为输入数据。在输入数据中各加入8%的扰动，分别进行储层物性参数估计，结果如图10所示。通过对比图10可以看出，基于三种模型估计得到的储层物性参数精度基本一致，证明模型的不同不会给估计结果带来较大的影响。因此本文方法可以适用于多种不同岩性、不同岩石物理特点的储层，只需在应用过程中根据储层特征建立合理的岩石物理模型，获取准确的模型参数。

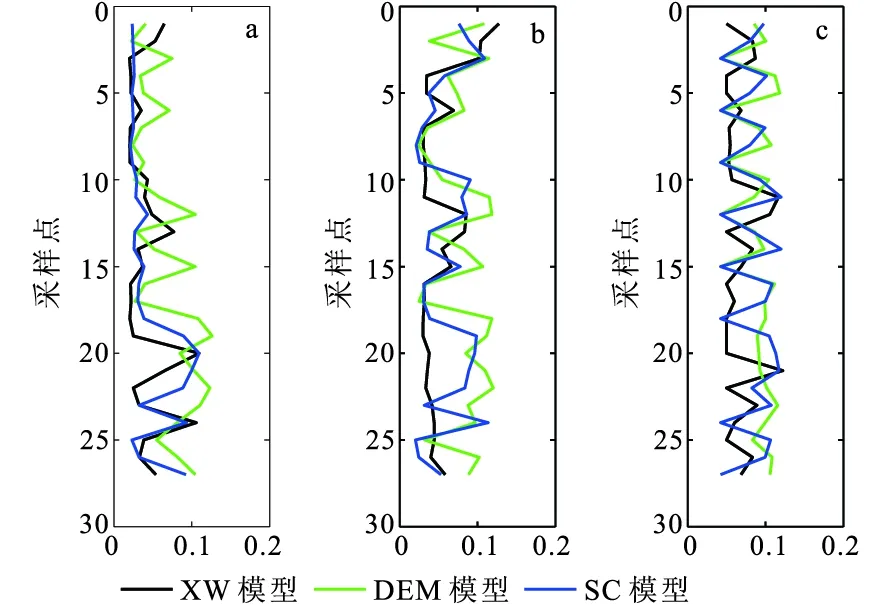
图10 不同模型的估计结果相对误差比较Fig.10 Comparison of relative estimation errors with different models(a)孔隙度；(b)泥质含量；(c)含水饱和度

3 实际应用

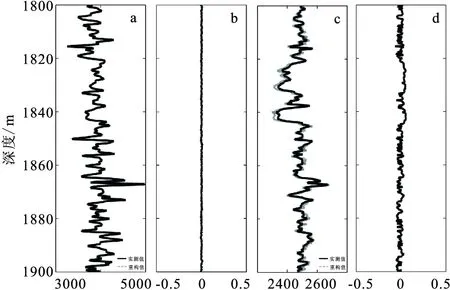
图11 利用Xu-White模型重构得到的纵横波 速度及相对误差Fig.11 Comparison of rebuilt velocity data and measured data using Xu-White model(a) 纵波速度实测值和重构值；(b)纵波速度相对误差；(c) 横波速度实测值和重构值；(d) 横波速度相对误差

图12 储层物性参数的估计结果与实际测量值的对比Fig.12 Comparison of estimated reservoir parameters and the measured data(a) 孔隙度； (b)含水饱和度；(c)泥质含量

将笔者提出的储层物性参数估计方法应用于中国某油田的实际资料。该工区的储层是碎屑岩储层，主要矿物组成是石英和粘土。为了利用测井得到的弹性参数数据估计出储层的物性参数，首先需要结合岩心实验等数据建立合适的岩石物理模型并确定模型的基本参数。经研究发现Xu-White模型能够较好地描述储层的岩石物理特点。利用Xu-White模型进行地层纵、横波速度曲线的重构，结果如图11所示。由图11可以看出与实际测量值相比，纵波速度的重构值非常准，误差极小；横波速度的重构值较为准确，误差略大于纵波速度的误差，在1 820 m～1 850 m之间的两处储层处误差相对大一点。但是误差的绝对值小于5%，精确程度可以满足储层物性参数估计的需要。准确的重构结果进一步证明了Xu-White模型对于该工区的储层是合适的。

基于Xu-White模型进行储层物性参数的估计。以体积模量、泊松比和密度的测井曲线作为输入数据，其中密度曲线是实际测井得到的，体积模量和泊松比需要利用实际测井得到的纵横波速度和密度计算得到。利用本文方法可以得到如图12所示的储层物性参数估计结果。通过对比图12(a)、图12(b)、图12(c)以看出，估计结果较为准确，证明方法具有一定的实用性。

4 结论

基于岩石物理理论提出了一种模型约束的岩石物理逆建模方法，可以从弹性参数中同时估计出孔隙度、泥质含量和含水饱和度三种储层物性参数。在输入参数没有误差的情况下，估计结果是较为准确的；当输入数据中包含误差时，由于模型约束可以有效地提高估计结果的稳定性，估计结果的精度也较高。本文储层物性参数估计方法是在岩石物理建模的基础上提出的，岩石物理模型的建立至关重要，根据储层特点建立准确的岩石物理模型有利于得到高精度的估计结果。

附录

微分等效介质模型(DEM模型)

微分等效介质模型是通过往固体矿物相中逐渐加入包含物相来模拟双相混合物的。利用微分等效介质模型(DEM模型)计算岩石骨架的模量，等效模量K*和μ*的耦合微分方程分别是：

(A-1)

(A-2)

初始条件是K*(0)=K1，μ*(0)=μ1，其中K1、μ1是基质的体积模量和剪切模量；K2、μ2是逐渐加入的包含物的体积模量和剪切模量，y是包含物的含量，P(*2)和Q(*2)是背景介质中包含物形状的表达式。

自相容近似模型(SC模型)

自相容近似模型通过用暂时尚未知的有效介质来替换背景介质，以此来近似包含物之间的相互作用，该方法考虑了包含物之间的相互作用，因此可以用于孔隙度较大的岩石。自洽模型公式是由Berryman给出的N相介质混合物的自相容近似表达式：

(A-3)

(A-4)