激电中梯装置测量长方异常体的三维正演模拟及启示
曹创华, 邓 专, 康方平,, 柳建新, 童孝忠
(1. 湖南省地质调查院, 长沙 410116;2. 中南大学 地球科学与信息物理学院, 长沙 410083;3. 中南大学 有色资源与地质灾害探查湖南省重点实验室, 长沙 410083)
0 引言
激发极化法在有色金属矿床勘探领域发挥了重要的作用,自使用以来发现了大批硫化物矿床[1-3]。特别是在大于万分之一图幅矿产调查研究阶段,因效率高、可以旁侧等特点,激发极化法中间梯度法装置在面积性工作时发挥了很大的作用[4-9]。但在实际应用之中,目前中间梯度法测线布设方位问题鲜有文献资料进行叙述参考文献[10]也仅仅直接给出结论:测线方位需垂直研究区主要目标体方向,但在实际工作中不可能完全垂直地质异常体。究其原因,笔者在对承担的项目实际探测资料分析以及查阅其他技术人员的实测资料时发现:矿区地质目标体在地层中走向往往不一,或者由于地形地貌原因,使得在布设测线时不同的技术人员测线方位不尽一致,随之其在地表探测出的数据不尽相同,最后导致地质解释不同而存在了不同程度的偏差。从这一现象出发,利用有限单元法进行了激发极化法中间梯度装置条件下的三维正演,接着分析了数值计算的有效性,最后根据实际的常见地质条件和施工参数设计了模型进行了激电中间梯度法剖面和异常走向不同夹角的模拟计算,得出了具有实际意义的结论,为勘查地球物理技术工作者提供了借鉴。
如图1所示,激电法勘探在实际布设电极时的供电源A极(或者B极),在数据采集区域的中间2/3区间可近似均匀电流场的区域进行测量[10],若中间区域地层中有异常体存在,则均匀场发生变化,在野外通过测量M极和N极之间电性参数来研究地质体电阻率变化。理论上的研究方法具体有:①物理模拟;②数值模拟。物理模拟是通过实验室物理实验模拟真实物理过程的方法,将实际地形物理的缩小模型置于实验体(如风洞、水槽等)内,在满足基本相似条件(包括几何、运动、热力、动力和边界条件相似)的基础上,模拟真实过程的主要特征[11];而数值模拟是依靠电子计算机,结合有限元、有限差分和有限容积的概念,通过数值计算和图像显示的方法,达到对工程问题和物理问题乃至自然界各类问题的研究[12]。近年来,随着电子计算机技术的发展,因室内数值模拟成本低,速度快而受推崇,数值模拟目前利用最多的是有限单元法(FEM)和有限差分法(FDM)法,有限差分法以计算方法简单速度快为特点,但对异常体的边界模拟精度有限,而有限单元法对异常体和测量剖面的边界拟合精度较高,其中王家林教授[13]课题组利用积分方程法模拟了低电阻率差情况下偶极-偶极剖面三维激电法正演,加快了计算速度;强建科博士[21]利用有限单元法数值模拟了单个剖面上偶极-偶极、单极-偶极、对称四极等装置条件下地质异常体响应规律;刘海飞等[14]实现了起伏地形电导率连续变化条件下利用单极-偶极装置的响应三维模拟,较好地反映了异常体的规模和空间形态。随着计算机性能的提高,谭捍东教授[15-16]课题组以CUDA为基础,利用MPI并行技术对电法勘探进行了三维数值模拟,大大提高了计算速度;戴前伟等[17]利用PSO-BP 非线性反演方法实现了二维Wenner-Schlumberger装置的规则异常体成像效果,证实了其方法垂直方向上的反演分辨率更高。在三维响应和成像规律的研究方面,崔益安等[18]利用二极装置研究了电法勘探三维正反演技术,把地球物理技术应用范围拓展到了污染监测领域,发现其具有良好的实用性和时效性。
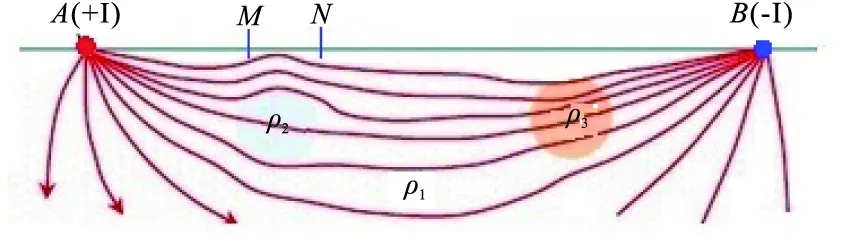
图1 激电法二维主剖面测量示意图Fig.1 The schematic diagram of two-dimensional principal profile measurement by IP method
我们发现目前在有色金属找矿技术领域,最为常用的中间梯度法装置扫面形式的数据研究甚有学者问津,加之笔者对以往工作中遇到的迷惑,因此利用有限单元法,针对供电电源为三维场源、计算了激电中间梯度法地表面积性测量条件下进行了三维数值,以期从本质上对激电扫面中间梯度法测线布设有一个客观的认知。首先参考黄俊革、强建科等[19-22]已有成果推导了三维场源的变分公式,然后设计层状模型计算了解析解和数值结果进行对比;最后设计了符合实际工作地电参数的模型,计算了激电中间梯度装置条件下二度地质异常体的走向和测量剖面方向之间不同夹角面上响应,分析并讨论了理论计算结果。
1 正演响应计算原理
正演响应是利用设计的地电模型,根据电场的特征和边界条件进行室内数值计算,得出其在特定装置下在地表的响应(图2)。
采用有限单元法,经过单元剖分、插值,单元积分、单元集成等来计算电场值,根据装置参数等地电观测数据计算激电中间梯度法条件下的面积性视电阻率和视极化率平面分布。

图2 二度体正演模型三维模型示意图Fig.2 The model diagram two-dimensional body forward model in three-dimensional
1.1 变分方程
为了更好地对一定角度的异常体模拟,且网格能够均匀的分布在测量区域,利用三角剖分进行插值,通过构造变分进行推导,得到三维电场的边值问题与下列变分问题等价[21]:
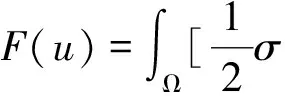
δF(u)=0
(1)
式中:I为电流强度;j表示电流密度矢量;U为总电位;σ表示介质的电导率;Ω为计算内部区域闭合空间;Γ计算区域内部的电阻率界面;r为点电源和计算点之间的距离;A为地表计算的点位置。
1.2 有限单元法
利用有限单元法对式(1)进行计算,对图3(a)中的三维地质体进行剖分,在测量区域剖分为三角柱状体。

(2)
将kij(其中i,j=1,2,…,6)集合呈矩阵形式,可得式(3)。
(3)
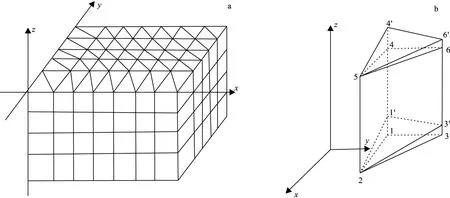
图3 有限元剖分模型示意图Fig.3 Typical finite-element mesh(a)三维地质体剖分示意图;(b)单个单元剖分示意图
依据上面系数组成单元刚度矩阵如下:
(4)
则式(1)中的第二项可变换为式(5)。
(5)
式中积分只与电源点有关。第三项积分与边界有关,若单元e的一个面1254落在无穷远边界上时,其系数矩阵为式(6)~式(7)。
(6)
(7)
同理,当单元e的面1463落在无穷远边界时,系数矩阵为式(8)。
当单元e的面123落在向下无穷远边界时,系数矩阵为式(9)。
(8)
(9)
F(u)= ∑Fe(u)=
(10)

KU=P
(11)
式中:K为系数矩阵;U为电位向量;P为与点源有关的向量,解方程组得各节点的电位值U。然后通过计算响应场值,然后按照式(12)~式(14)计算激电中间梯度法视电阻率和视极化率值[23]。
(12)
(13)
即可计算MN测量点之间的视电阻率,其中AM、AN、BM、BN、MN为极距之间的距离,ΔUMN为M和N极之间的电位差(图1)。为了衡量矿化物的直接激发极化大小特征,根据异常体响应条件下的二次场和总电压比值来计算其大小[24]。
(14)
式中:ΔU2为MN之间的供电电源断开后的二次场电位差。
2 正演算法正确性验证
设计了三层H型地层结构的一维介质,具体参数为:第一层电阻率50 Ω·m,厚度5 m;第二层电阻率10 Ω·m,厚度5 m;第三层电阻率200 Ω·m。正演响应的解析解用一维层状模型递推公式进行迭代计算,数值解按照模型设计利用本文中的计算方法计算,其计算结果见表1。由表1可以看出,在18个极距中,最大误差为3.26%,说明精度相对较高,数值计算结果较为可信。

表1 层状模型数值解和解析解计算结果
3 三维正演模拟
按照高斯坐标系度量,沿x轴、y轴和z轴方向分布的地质体为1 200 m×800 m×400 m,设计的二度体模型及相关参数见图2。模拟空间坐标为x=[0, 1200]m,y=[-200, 600]m,z=[0, -400]m。异常体以[600,200,-60] m为中心,其大小为200 m×30 m×30 m的低电阻率和高极化率异常体,电阻率围岩为4 000 Ω·m、异常体为10 Ω·m;极化率围岩1%、异常体10%。

图4 中间梯度法测线方位和异常体夹角变化下扫面正演结果Fig.4 Forward result under the change of the angle between the azimuth line and the anomaly body in the middle gradient method(a)夹角为0°视电阻率扫面模拟结果;(b)夹角为0°视极化率扫面模拟结果;(c)夹角为30°视电阻率扫面模拟结果;(d)夹角为30°视极化率扫面模拟结果;(e)夹角为60°视电阻率扫面模拟结果;(f)夹角为60°视极化率扫面模拟结果;(g)夹角为90°视电阻率扫面模拟结果;(h)夹角为90°视极化率扫面模拟结果
研究了测线MN和异常体走向在地表夹角0°(测线方位和异常体走向一致)、夹角30°、夹角60°和相互垂直时的激电扫面结果(图4),其中点距为5 m,线距为10 m,保证跨越异常体的为主至少有三个响应测点。图4中,随着异常体和测线夹角的增加,扫面结果和异常体的地表投影逐渐趋于一致,且视电阻率对测线方位不同的测量结果敏感程度大于视极化率。在夹角为0°时,视电阻率被分为两个对称的相对低阻体;当夹角为30°时,两个对称的低阻异常峰值减小且与两个峰值之间的电阻率差异越来越小;当夹角增加到60°时,两个对称的低阻异常峰值几乎未能发现,但异常体的边界与地表下的异常体投影有一定的偏差;当夹角增加到90°时,异常体的地面投影和扫面结果完全对应,说明夹角过小时测量的异常是不可信的。虽然视极化率没有视电阻率明显,但是随着角度的增加异常的幅值逐渐增大,异常得到强化,说明在实际野外测线进行布置时需要尽量的垂直主要构造或者矿(化)体。
为了量化测线和异常地质体走向对对异常体测量的影响,特抽取了主剖面数据(图4中的蓝色实线),研究了随着异常的走向的变化得到的结果(图5)。当异常体和测线平行时,其面上视电阻率不仅出现了两个峰值且位置与中心测点不对称,其视极化率也出现了负值,随着两者夹角的增加,异常逐渐得到正确的显示。明显的当两者夹角大于60°时对异常的定性影响较小。
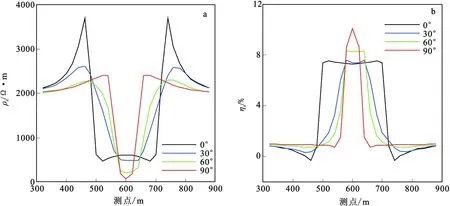
图5 中间梯度法测线主剖面不同角度测量数据正演结果Fig.5 Forward grades of survey data at different angles in main profile of intermediate gradient method(a)测量主轴视电阻率扫面模拟结果;(b)测量主轴视极化率扫面模拟结果
4 结论
通过以上分析,我们利用有限单元法正确模拟了激电法三维模拟,特别是从实际勘查角度出发,研究了激电中间梯度法测量时其剖面和异常体地质走向呈不同夹角时的响应规律,主要结论如下:
1)实现了激电中间梯度法条件下的三维数值模拟,设计了模型计算了地表扫面数据的响应。
2)通过计算发现,不同正演响应数据其对测线布设方位敏感不一,通过对视电阻率和视极化率的正演响应结果对比来看,随着两者夹角的减小视参数数值差异越小,对后期的正确解释困难也随之增加。
3)激电中间梯度法的测线方向应尽可能的垂直异常体走向,如果研究区域异常沿其走向存在连续性和对称性,可考虑变换方位进行测量以研究地质异常体是否为一个异常。可以通过改变测线方向,用异常相交的方法定位异常源的顶板中心位置。
4)一个研究区一般情况要求布置相同的测线方向,不同时期的物探资料如果测线方位不同,即不能简单的进行拼接和比较,以免在综合研究分析时产生误导。

