不同质地重塑土坡面细沟侵蚀形态与水力特性及产沙的关系
倪世民,冯舒悦,王军光,蔡崇法
(华中农业大学水土保持研究中心,农业部长江中下游耕地保育重点实验室,武汉 430070)
0 引 言
细沟侵蚀通常被认为是水力侵蚀产沙中最重要的过程,是WEPP模型侵蚀产沙的核心[1]。研究表明,细沟的发育程度对侵蚀有重要影响[2],细沟形成后土壤侵蚀量将会显著增加[3-5]。水流的侵蚀力与坡面土壤的抗蚀性是影响细沟发生的两大因素[6],坡面细沟形态是水流水力学特性与坡面土壤相互作用的结果[7],三者间形成了一个复杂的互反馈过程[8-9]。一方面,细沟的形成导致径流汇集且趋向紊乱,径流性质的转变引起侵蚀量的急剧增加,径流流态与径流的输沙能力发生了变化[10-11];另一方面,径流侵蚀能力与输沙能力增加,又加剧了细沟形态的演变,尤其在黏粒含量低的土壤坡面上细沟形态的演变更剧烈[12]。蔡强国等[13-14]研究指出,坡面侵蚀产沙的变化过程与细沟形态变化过程基本一致。因此,不能把坡面侵蚀过程中的水力学特性、细沟形态特征及侵蚀产沙特征隔离出来单独研究。定量描述细沟的形态特征,揭示其与水力学特性、坡面产沙特征之间的定量关系,是建立坡面侵蚀产沙预报模型的基础。
近些年来,相关学者对细沟形态特征与坡面侵蚀产沙的关系开展了大量的研究工作。雷廷武和Nearing使用砂壤土进行室内水槽试验,得出了砂壤土细沟输沙能力的最适采样长度为2~4 m[15];Shen等[16]设置了室内模拟与野外监测对比研究的方法,建立了黄土坡面细沟侵蚀预报模型;Bruno等[17]通过天然降雨试验对一种黏壤土的细沟横断面和长度等变化规律进行了研究,并得出了细沟侵蚀与细沟间侵蚀分别对土壤侵蚀的贡献率;以及还有其他学者运用各种手段以不同土壤作为研究对象,取得了丰硕的成果[18-21],但是他们的试验材料主要集中在一种或少数几种土壤质地、颗粒组成的土壤,缺乏系统地考虑土壤中黏粒含量的改变对细沟侵蚀形态与侵蚀产沙的影响。研究表明,土壤质地影响细沟形成前后泥沙颗粒大小的分布[22],是影响土壤抗蚀性的重要因素,土壤组成颗粒越细,黏结力越强,抗侵蚀的能力也越高[23]。土壤类型对土壤的抗蚀性具有重要影响[24],黄土的细沟侵蚀能力是红土的1.5倍[25]。不同质地的土壤坡面的细沟形态特征、径流含沙量与土壤侵蚀速率方面存在较大差异[26-27]。赵春红等[28]认为土壤质地对细沟宽深比参数有显著影响,土壤质地越细,宽深比指数越小。此外,由于国内外学者所使用的研究方法与测量手段不尽相同,不同试验材料的研究成果间缺乏系统的横向对比分析,试验材料间的差异性与土壤侵蚀过程的复杂性限制了研究结果的应用范围,使得研究成果仅仅适用于特定土壤或少数几种类型土壤条件。因此,有必要系统地对不同颗粒组成的土壤进行细沟侵蚀形态与产沙特征对比研究,探究在同一试验条件下不同质地土壤的细沟形态特征与侵蚀产沙的规律。
鉴于上述研究背景与存在的问题,本文通过室内模拟径流冲刷动床试验的方式,以土沙混合配制不同颗粒组成的重塑土坡面为研究对象,人为控制土壤的质地与胶结强度,系统地对比分析不同试验条件下坡面的细沟形态特征,并探索水动力学参数与细沟形态参数、细沟形态参数与侵蚀坡面产沙之间的关系,以期在获取坡面细沟形态参数与土壤性质的基础上,获得可信度较高、有效性较好的侵蚀预测方程,并为不同类型或颗粒组成的土壤和类土沙混合体(如工程堆积体、崩岗崩积堆等)的坡面侵蚀预测与土壤侵蚀机理研究提供一定的理论基础与参考依据。
1 材料与方法
1.1 试验材料
供试土样所需的黏土为第四纪红黏土发育的林下表层(0~15 cm)红壤,采自鄂南丘陵区咸宁市咸安区贺胜桥镇(114°41' E,30°01' N),所需的沙土为普通工程沙土。将土样去除石块、根系等杂质,自然风干过5 mm筛网备用。本试验设置0%、30%、50%、70%、100% 5种含沙量的混合结构土样作为研究对象[29,30],分别被定义为 S1至 S5,各个处理的土样用搅拌机干拌充分混合均匀。土壤基本理化性质采用常规方法测定[31],见表1。按美国土壤质地分类制,5种含沙量的混合结构土样从 S1至S5依次为粉质黏土、黏土、砂质黏壤土、砂质壤土、沙土。

表1 试验土样的基本理化性质Table 1 Basic physicochemical properties of specimen used in experiment
1.2 试验设计
本研究以室内放水冲刷动床试验的方式进行,试验装置如图1所示。试验土槽为移动变坡式大型钢制土槽,由两部分组成:(1)主体土槽规格:长、宽、高依次为3.0 m、1.0 m、0.35 m,分为相同的2个平行土槽,坡度可以在 0~30°的范围内自由调节,土槽边沿每隔 20 cm画有红白相间的刻度线以辅助测量;(2)土槽后端为稳流箱,内部上下交错有 2块不锈钢消能板,以保证水流平稳流入土槽。供水设备主要由蓄水池、水泵、阀门和水管组成,放水流量由阀门控制。
填土容重控制在1.35 g/cm3,接近田间自然状况。为了控制填土过程土壤密度保持一致,采取分层填土,边填边压实,填装上层土壤前,抓毛下层土壤表层,防止出现分层现象。装土结束后,用水平尺刮平土壤表面。在坡顶覆盖15 cm长的纱布,尽量削弱稳流箱出口跌水能量与边缘效应的影响。每次试验前在坡面上覆盖一层纱布,使用模拟降雨器以小雨强进行预湿润,用MP-406土壤水分测定仪测得含水率降至30%时开始进行试验。
根据南方红壤坡面的常见坡度,试验设置5°(缓坡)和15°(陡坡)2个坡度,设置2、4、6、8 L/min 4个流量,试验流量按照南方特大暴雨在径流小区上产生的单宽流量换算到试验土槽上得到,每组试验设置2个平行。为了减少细沟间侵蚀过程的影响,更准确地研究坡面细沟侵蚀产沙与侵蚀形态的关系,考虑到不同含沙量的坡面进入细沟侵蚀阶段时间不一致,结合前期的预试验,本试验设置计时从坡面明显形成股流与细沟时开始[13,32],试验时间设置为 15 min。通过预试验的观测发现,15° 坡度8 L/min放水流量条件下含沙量较高坡面侵蚀强烈,造成短时间内坡面的侵蚀地貌超过了细沟的范畴,从而未进行该条件下的模拟试验。水宽采用直尺法每隔 20 cm(测量区间20~280 cm)多次测定,采用接样瓶(每30 s)结合接样桶(每1 min)的方法测得含沙量、产沙量与径流量,表面流速采用高锰酸钾染色法分上中下 3个坡段测得,然后根据流态乘以相应的系数得到平均流速[33],水温从放置在稳流槽内的温度计读取。试验过程中用摄像机对整个试验过程进行拍照记录,试验结束后用直尺量取沟长,以及在刻度线处量20~280 cm区间沟深与沟宽数据。
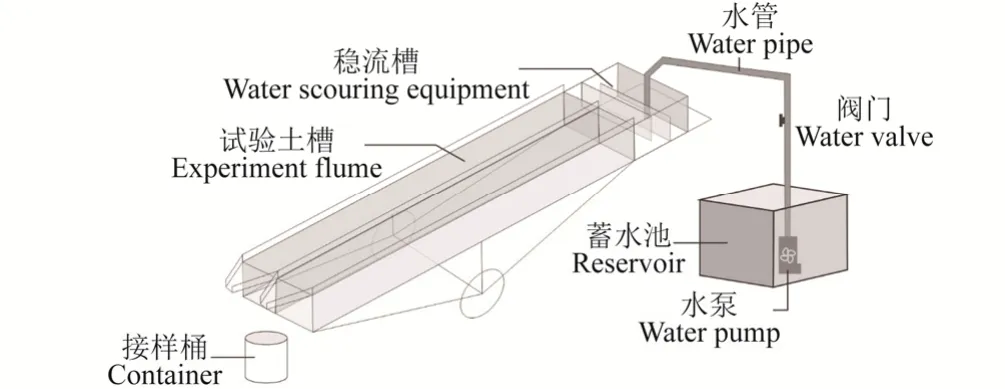
图1 试验装置Fig.1 Experiment apparatus
1.3 数据分析处理
土壤侵蚀速率:坡面在水流侵蚀动力的作用下单位时间、单位长度上的产沙量[34],其求解形式为:

式中:D为土壤侵蚀速率,kg/(m2·min);Sum为累计产沙量,kg;B为水宽,cm; L为沟长,m;T为试验时间,min。
水流剪切力:产生土壤颗粒剥蚀和输移泥沙的水流冲刷动力[35],其求解形式为:

式中:τ为水流剪切力,Pa;J为水力坡度,m/m,可用坡度的正弦值近似替代;R 为水力半径,m,本试验条件下可近似用水深h代替;ρ为水流容重,kg/m3;g为重力加速度,g = 9.8 m/s2。
根据相关学者[36]提出的水流功率的概念,水流功率可用下式进行求解:

式中:ω 为水流功率,N/(m·s);V 为坡面平均水流流速,m/s。
根据Yang[37]定义的单位水流功率的概念,单位水流功率可用下式求得;

式中:Pr为单位水流功率,m/s。
坡面流的流态通过水流内部的紊乱指标来描述,通常使用的判别参数为雷诺数与弗汝德数[38]:
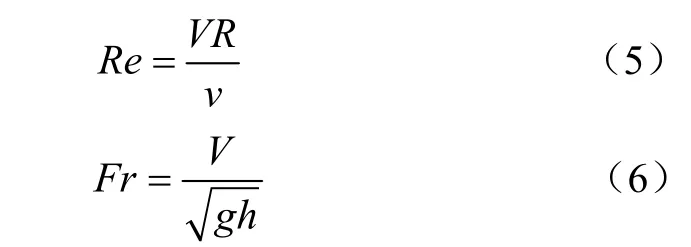
式中:R 为水力学半径,由水深代替,m;v 为粘滞系数,cm2/s。
本研究采用纳什效率系数[39](NSE)、决定系数(R2)、均方根误差(RMSE)来衡量拟合函数或模型的有效性,筛选适用于试验条件的结果,其求解形式为:
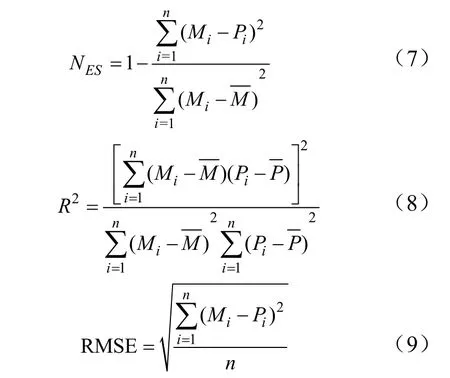
式中:Mi为实测值,为实测值的平均值,Pi为预测值,为预测值的平均值,n为样本数。决定系数(R2)与纳什系数(NES)联合评价方法在评价土壤侵蚀模型有效性方面的适宜性已得到一些研究者验证[40]。R2能够表征实测值与模拟值相关的密切程度[41],NES能够表征模型的可信程度[42],R2和NES越接近1,模型的有效性越高。
数据处理与分析通过Excel 2016、Origin 2017与SPSS 19.0软件完成,相关分析采用Spearman双侧显著性检验。
2 结果与讨论
2.1 细沟形态参数特征
试验条件下,细沟最终长度都接近于坡面长度(2.85 m),差异不显著,故本文选取了细沟平均沟深 hr、平均沟宽dr和宽深比 µ作为描述细沟形态特征的参数。沟深和沟宽是细沟断面形态的基本要素,能够直观地描述细沟断面尺寸的大小;细沟的宽深比 µ是无量纲参数,表征细沟断面形态在水平方向和竖直方向尺寸的相对大小,Mancilla等[43]认为通过测量宽度和深度而得到的细沟断面的变化能够表征细沟发育情况。宽深比的值越大,细沟断面形状越近似“宽浅式”,宽深比的值越小,细沟断面形状越近似“窄深式”,其数学表达式为

图2、图3、图4分别是不同试验组合下细沟平均沟深、平均沟宽以及宽深比的分布规律。由图2可知,细沟的平沟深随着坡度和流量的增大而增大,随着坡面含沙量的增加呈单峰状分布,当水流侵蚀力较小时沟深整体上在S2坡面处取极值,随着坡度和流量的增大,最大值依次从S2坡面(70%含沙量)转为S3坡面(50%含沙量)、S4坡面(30%含沙量)。这是因为混合土样中黏土母质发育的红壤具有良好的抗蚀性与黏结力[23,44],含沙量的增加使坡面稳定性降低,不易形成稳定的沟壁;但与此同时含沙量的增加使土壤的抗蚀性降低,水流侵蚀力的增加促使下切侵蚀加剧,细沟加深,因此在S1到S5中间某个含沙量的坡面(如S3、S4)形成的出现了最大的沟深。

图2 不同试验条件下平均沟深的分布Fig.2 Distribution of mean rill depth under different test conditions
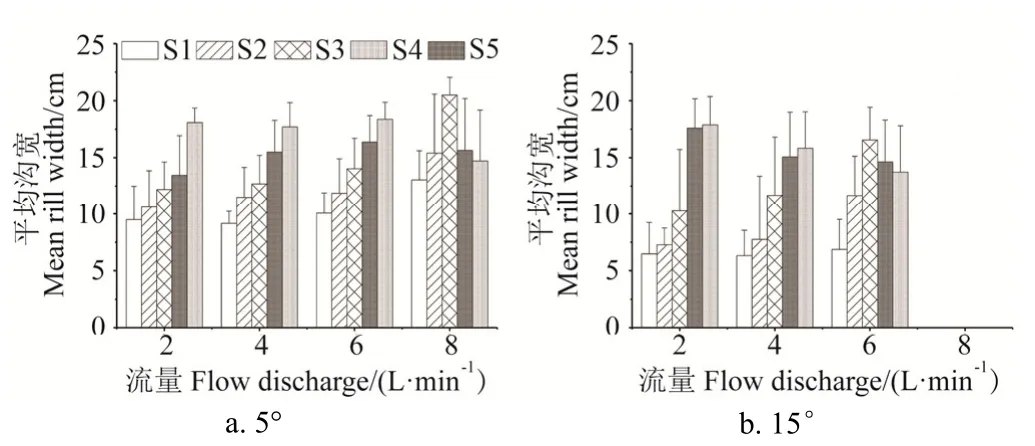
图3 不同试验条件下平均沟宽的分布Fig.3 Distribution of mean rill width under different test conditions
从图3可以看出,在2个坡度下,S1、S2、S3组合细沟平均沟宽随着流量的增加而增加,S4、S5组合细沟平均沟宽随着流量的增加而减少,表明坡面黏粒含量较少的坡面对较大的径流侵蚀力更加敏感。不同坡度下,S1、S2、S3组合细沟平均沟宽随着坡度的增加而减小,S4、S5组合细沟平均沟宽变化不明显。细沟的平均沟宽随着坡面含沙量的增加而增大,当水流侵蚀作用较强时则呈单峰状分布(如5°坡度8 L/min放水流量),在S3坡面取最大值。造成上述现象的原因可能是坡度的增大使细沟水流的剪切力和输沙能力变大,在含沙量低的坡面上沟壁稳定性较强,水流的下切侵蚀作用占主导,沟宽的增加主要是由沟壁的坍塌或滑塌引起;而在含沙量高的坡面(如S4、S5),土壤黏结力较差,水流对坡面的侵蚀主要是以层状剥蚀为主,细沟的下切伴随着沟宽的增加。细沟流的流态从另一角度印证了上述现象(见图4)。根据明渠流的判断标准[45],细沟流流态多属于层流与过渡流的范围,且随着坡面含沙量的增加流态逐渐趋向层流与缓流。从能量的角度分析,坡面的侵蚀过程是一个能量耗散的过程,细沟的输沙产沙与能量的耗散密切相关[46]。结合细沟形态,细沟流流态的分布规律从侧面反映了不同坡面的径流剥蚀形式。
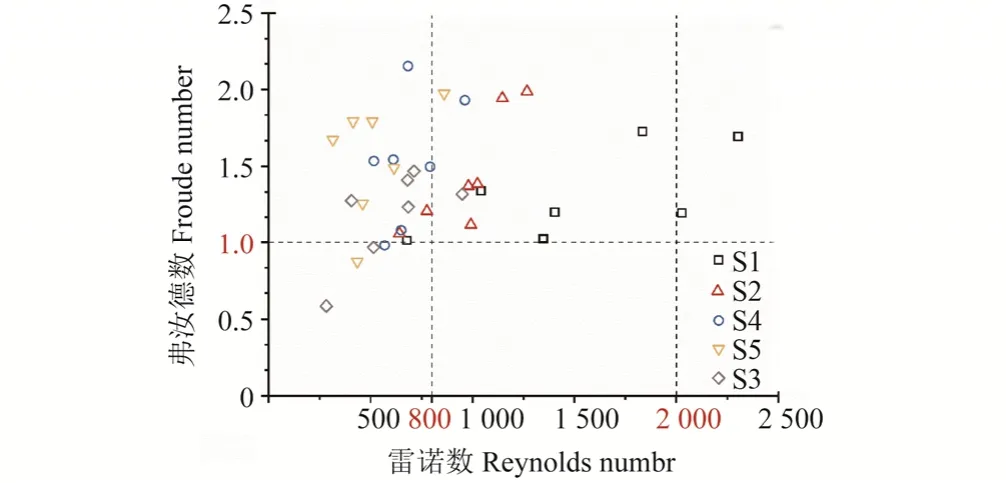
图4 坡面含沙量对径流雷诺数与弗汝德数的影响Fig.4 Effects of different clay-sand mixtures on the Reynolds number (Re) and Froude number (Fr)
分析细沟宽深比(见图5)发现,细沟宽深比随坡度和流量的增加呈逐渐减小的变化趋势。随着坡度和流量的增大,细沟内的水流侵蚀力增强,单位水流动力增大,水流强烈的下切侵蚀致使细沟断面形态趋向于“窄深式”,宽深比逐渐减小。和继军等[47]研究发现细沟宽深比随着坡度增大逐渐减小,本试验结果与其呈现相同趋势。对于不同含沙量的坡面,坡面土壤从粉质黏土(S1)到砂土(S5)的过程中,细沟宽深比参数整体上逐渐减小,细沟逐渐从“窄深式”向“宽浅式”发展。上述结果与赵春红等[28]的分析结果相符合。S1坡面试验材料为粉质黏土,宽深比参数介于0.70~5.00之间,平均值为1.83,结果与 Bruno等[17]对粘土质地的野外小区细沟宽深比的试验结果较为一致(平均值1.51)。由于砂粒含量高的坡面沟底下切与沟宽增加是同步发生,其结果造成砂粒含量高的坡面宽深比较大,细沟断面趋向“宽浅式”形态。可以看出,土壤质地对坡面侵蚀形态具有重要影响[26-27]。
2.2 水动力学特性与细沟形态特征的关系
坡面水流是细沟产生的根本侵蚀力,细沟的形态特征是细沟水流与边壁土壤冲刷塑造的结果,而同时细沟的断面形态也影响着坡面细沟水流水动力学特性[48]。研究动床条件下细沟水流的水动力学特性与细沟形态参数之间的关系,对于准确认识坡面细沟的形成和发育机制具有重要意义。
表 2所示为试验参数的关系矩阵,由表可知细沟形态参数和水力学参数之间存在高度相关关系。坡度、平均流速、水流剪切力、单位水流功率、水流功率与平均沟深、宽深比的关系密切,呈极显著相关关系(r>0.60,p<0.01),相关系数的大小顺序为Pr>S>ω>τ>V。水流剪切力和水流功率与平均沟宽呈显著负相关关系(r分别为-0.496和-0.445,p<0.01),其他参数和平均沟宽关系不显著。坡面材料的差异性造成坡面糙度、侵蚀泥沙颗粒粒径、细沟沟壁稳定性、土壤可蚀性、临界地形因子等存在差异[49-50],这可能是细沟平均沟宽与水力学参数相关关系较差的原因。上述结果表明,当描述水力学参数与坡面细沟形态的关系时,单位水流功率与水流功率是最适合的参数指标。

图5 不同试验条件下细沟宽深比Fig. 5 Rill width-depth ratio under different test conditions
因此,本文选取细沟形态参数(沟深、宽深比)与水力学参数(单位水流功率、水流功率),对它们之间的关系进行拟合发现,幂函数关系可以很好地解释水力学参数与细沟形态参数之间的关系(表3)。由表3可知,单位水流功率与细沟平均沟深、细沟宽深比的回归方程决定系数分别为0.803与0.859(p<0.01)。单位水流功率反映了作用于侵蚀床面泥沙的单位质量水体所具有的势能随时间变化率,是一个包含流速与坡度的综合性参数[35]。相比水流功率而言,单位水流功率更适合用于描述细沟形态特征。
2.3 细沟形态特征与坡面产沙的关系
由表 2中可知,细沟侵蚀速率、坡面累计产沙量与沟深、细沟宽深比呈极显著相关关系,相关系数达到0.88以上,表明细沟的形态变化与坡面细沟侵蚀的强度具有同步性,细沟形态的变化可以反映坡面产沙的变化,而沟宽的发育由于受坡面含沙量和水流侵蚀方式的干扰影响,与坡面产沙并未表现出显著的相关关系。上述分析表明沟深与宽深比是表征坡面侵蚀产沙最佳的细沟形态参数,能够很好地体现坡面侵蚀发育程度,可以用幂函数表示它们之间的关系。由表 4可知,沟深对坡面产沙最为敏感(R2>0.787,NES>0.793,p<0.01),函数达到了预报精度要求。
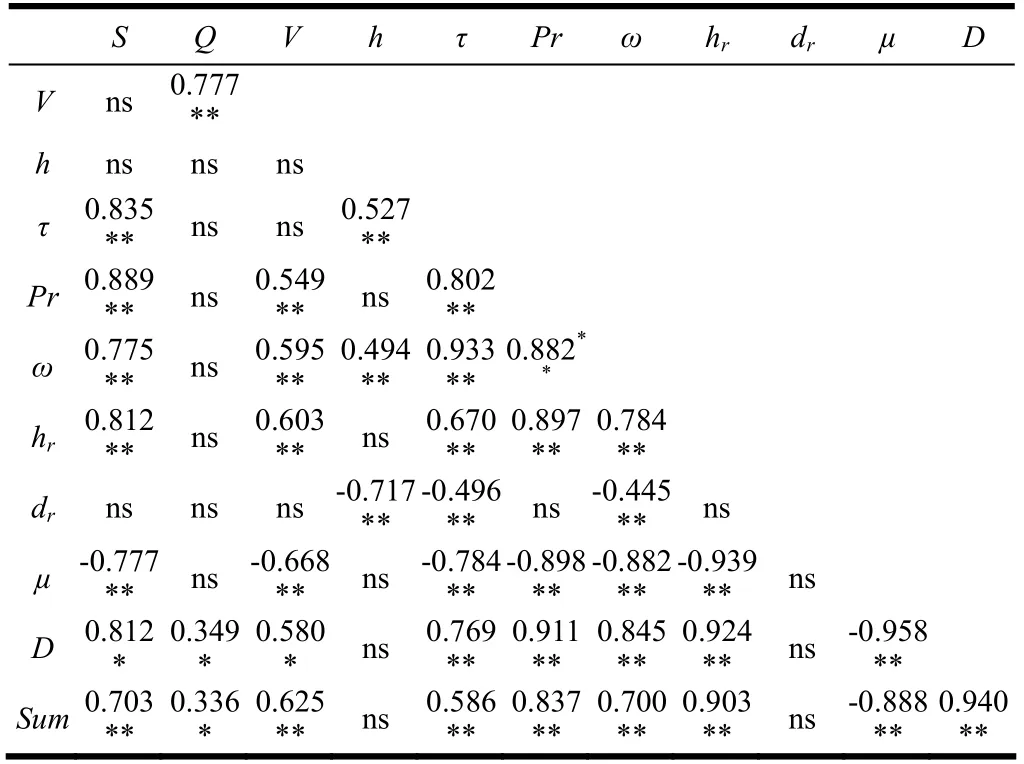
表2 试验参数的相关关系矩阵Table 2 Correlation matrix of test parameters

表3 水力学参数与细沟形态参数的关系Table 3 Relationship between hydraulic parameters and rill morphology parameters
坡面细沟形态与侵蚀产沙是一个相互关联、彼此制约的动态耦合系统,内外侵蚀营力的作用使细沟的产生较为复杂[51],上述单因子指标预报坡面产沙过于概化,为此,本文引入了细沟形态综合量化参数。为了确定细沟形态对坡面产沙的综合影响,以累计产沙量Sum为目标函数,选取与坡面产沙关系最为密切的参数沟深hr和宽深比µ作为自变量建立多元回归关系:
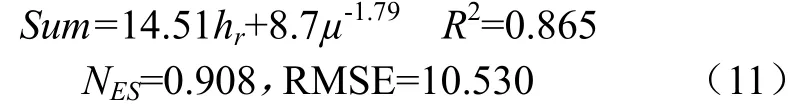
式(11)中2个系数表示2个参数对累计产沙量的影响率,可知,沟深和宽深比对累计产沙量的影响率分别为63%与37%,沟深的影响率大于宽深比。由此引入包含沟深、沟宽、宽深比 3个指标的无量纲参数——细沟形态综合量化参数 G,建立沟深、宽深比与综合量化参数 G之间的多元回归函数关系,三者关系如下:
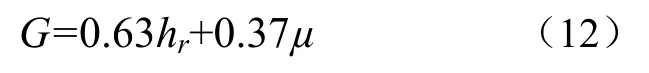

表4 细沟形态参数与坡面产沙的关系Table 4 Relationship between rill morphology parameter and slope sediment yield
对细沟形态综合量化参数与坡面侵蚀产沙参数之间的关系进行拟合,建立基于细沟形态参数预测侵蚀产沙的经验预测方程,拟合结果见表5。由表5可知,综合量化参数对于土壤侵蚀速率有较好的预测效果(R2>0.747,NES>0.755,p<0.01)。在本试验中,设置了不同含沙量的土沙混合结构坡面为研究对象。Ali等[52]在建立无粘性砂粒泥沙输移能力预测方程时引入了砂粒的粒径中度来表征不同粒径砂粒的性质;Kinnell[32]指出坡面输沙与土壤的粘聚力有关。此外,其他相关学者为提高所建立方程的适用范围,也提出了不同的参数来引入到预测方程的建立中[53-55]。针对本试验中坡面土壤颗粒组成的差异性,引入坡面土壤黏粒含量Cl定义不同土沙结构的坡面,建立基于坡面土壤性质与细沟形态参数的坡面侵蚀预测方程。对比分析未引入坡面土壤性质的预测方程,新方程的有效性显著提高(R2>0.879,p<0.01),方程的可信程度明显趋好(NES> 0.887),表明本研究通过土壤黏粒含量与细沟形态综合量化参数所构建的侵蚀产沙预报方程预测精度较高,预测效果比较理想。

表5 细沟形态综合量化参数与坡面产沙的函数关系Table 5 Functions between rill morphology comprehensive quantification parameters and slope sediment yield
3 结论
本研究通过在长3 m、宽1 m、深0.35 m的试验土槽上对不同颗粒组成的土壤坡面进行放水冲刷试验的方法,对细沟形态参数与坡面产沙特征的关系进行了探索,并引入了可以表征坡面土壤性质的黏粒含量,建立基于土壤性质与细沟形态参数的坡面侵蚀经验预测方程。结果表明:
1)整体上坡面细沟的平均沟深与平均沟宽随坡度的变化明显,两者随流量的变化不明显;细沟宽深比随坡度和流量的增加逐渐减小而增大(窄深式)。土壤的颗粒组成对细沟形态参数具有明显的影响作用,随着坡面含沙量的增加,细沟断面形态整体趋向“宽浅式”。
2)单位水流功率是描述细沟形态特征的最佳参数(r>0.897,p<0.01),幂函数关系可以很好地呈现单位水流功率与细沟形态特征的关系(R2>0.803,p<0.01)。
3)基于细沟的平均沟深与细沟宽深比的细沟形态综合量化参数能够很好地反映坡面侵蚀的强度,对坡面产沙均有较好的预测效果(R2>0.747,p<0.01)。引入坡面土壤黏粒含量显著得提高了坡面侵蚀预测方程的预测精度(R2>0.879,p<0.01)。上述结果为进一步研究坡面侵蚀的机理与预测提供了参考依据。

